2017-2018学年内蒙古满洲里市九年级上期末检测数学试卷含答案 10页

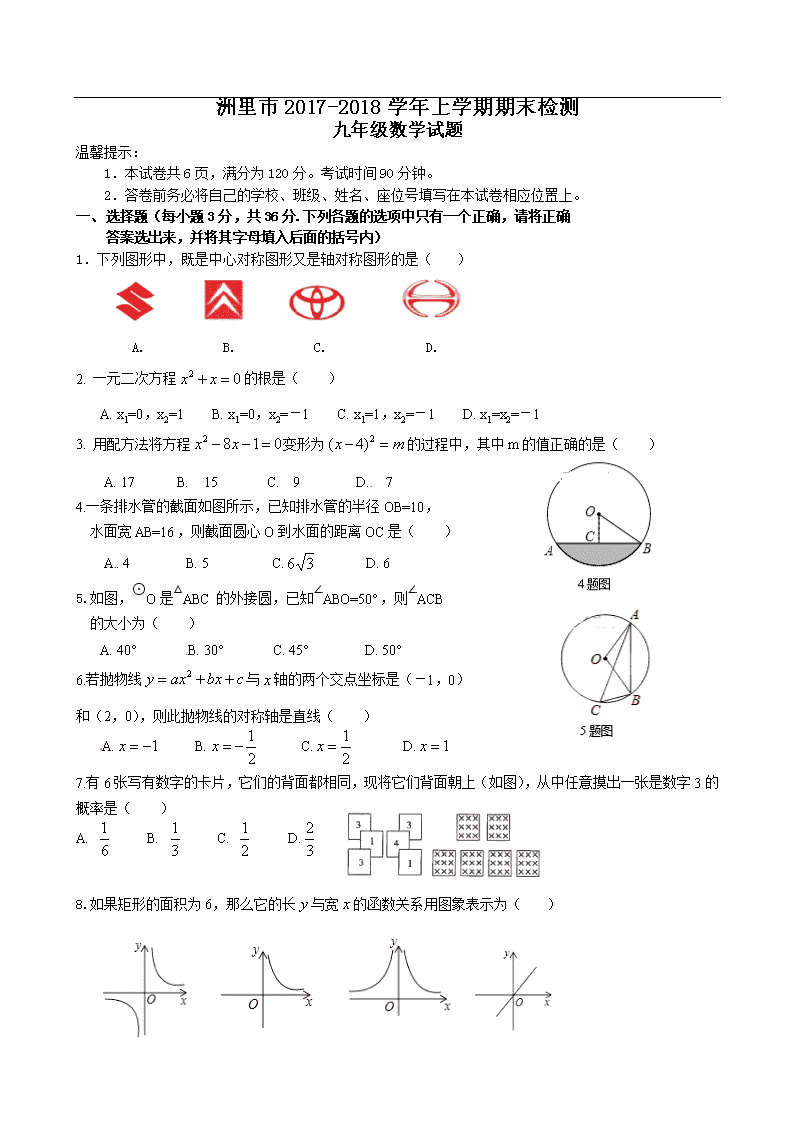
洲里市2017-2018学年上学期期末检测 九年级数学试题 温馨提示：‎ ‎1．本试卷共6页，满分为120分。考试时间90分钟。‎ ‎2．答卷前务必将自己的学校、班级、姓名、座位号填写在本试卷相应位置上。‎ 一、 选择题（每小题3分，共36分.下列各题的选项中只有一个正确，请将正确 答案选出来，并将其字母填入后面的括号内）‎ ‎1．下列图形中，既是中心对称图形又是轴对称图形的是（    ） ‎ ‎ ‎ A. B. C. D. ‎ 2. 一元二次方程的根是（　　） ‎ A. x1=0，x2=1 B. x1=0，x2=－1 C. x1=1，x2=－1 D. x1=x2=－1‎ ‎3. 用配方法将方程变形为的过程中，其中m的值正确的是（　　） ‎ A. ‎17 B. 15 C. 9 D. 7‎ ‎4.一条排水管的截面如图所示，已知排水管的半径OB=10， ‎ 水面宽AB=16，则截面圆心O到水面的距离OC是（   ） ‎ A. 4 B. 5 C. D. 6‎ ‎5.如图，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB ‎ 的大小为（   ） ‎ A. ‎40° B. 30° C. 45° D. 50°‎ ‎6.若抛物线与轴的两个交点坐标是（－1，0）‎ 和（2，0），则此抛物线的对称轴是直线（　　） ‎ A. B. C. D. ‎ ‎7.有6张写有数字的卡片，它们的背面都相同，现将它们背面朝上（如图），从中任意摸出一张是数字3的概率是（   ） ‎ A. ‎ B. C. D. ‎ ‎8.如果矩形的面积为6，那么它的长与宽的函数关系用图象表示为（    ） ‎ ‎ ‎ ‎ A. B. C. D. ‎ ‎9.如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A 按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在 同一条直线上，那么旋转角等于（   ） ‎ A. ‎55° B. 70° C. 125° D. 145°‎ ‎10.一次函数与二次函数在同一直角坐标系中的图象可能是（    ） ‎ ‎ ‎ ‎ A. B. C. D.‎ ‎11.在一幅长80cm，宽50cm的矩形风景画的四周镶等宽的金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400 cm2，设金色纸边的宽为cm，根据题意所列方程正确的是（    ）‎ A. B. C. D. ‎ ‎12．如图，有一圆锥形粮堆，其侧面展开图是半径为6m的半圆，‎ 粮堆母线AC的中点P处有一老鼠正在偷吃粮食，此时，小猫正 在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的 ‎12题图 最短路程长为（ ）‎ A．3m B． m C． m D．4m 二、填空题（本题6个小题，每小题3分，共18分）‎ ‎13.如果关于的方程没有实数根，那么的取值范围是 . ‎ ‎14.圆内接正六边形的边长为10cm，则它的边心距等于________cm． ‎ ‎15.在双曲线上有三个点A（x1，y1），B（x2，y2），C（x3，y3），‎ 若x1＜x2＜0＜x3， 则y1，y2 ，y3的大小关系是 ．（用“＜”连接） ‎ ‎17题图 ‎16.已知抛物线与轴的一个交点为（，0），则代数式的值为________． ‎ ‎17.如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，‎ 且∠AEB=60°，则∠P=________度． ‎ ‎18题图 ‎18.如图，将△ABC绕点C旋转60°得到△A′B′C′，‎ 已知AC=6，BC=4，则线段AB扫过图形（阴影部分）的 面积为 （结果保留π）. ‎ 三、解答题（本题4个小题，每小题6分，共24分）‎ ‎19.解方程：‎ ‎20.在平面直角坐标系中，△ABC的位置如图所示,(每个小方格都是边长 为1个单位长度的正方形)．‎ (1) 将△ABC沿轴方向向左平移6个单位 长度，画出平移后得到的△A1B1C1；‎ (2) 将△ABC绕着点A顺时针旋转90°,‎ 画出旋转后得到的△AB2C2，‎ 并直接写出点B2，C2的坐标．[来源:学§科§网]‎ ‎21.已知抛物线经过点（1，-2）‎ ‎（1）求的值；‎ ‎（2）若点A（m，y1）、B（n，y2）（m＜n＜3）都在该抛物线上，‎ 试比较y1与y2的大小．‎ ‎22.如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的 四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底 面积为800平方厘米.求截去正方形的边长. ‎ 四、（本小题7分）‎ ‎23.如图，△ABC 中，AB=AC，以AB为直径作⊙O，与BC交于点D，过D作AC的垂线，垂足为E．求证：DE是⊙O切线．‎ ‎　　　　　‎ ‎　　　　　　　　　　 ‎ 五、（本小题7分）‎ ‎24. 有A、B两组卡片共5张，A组的三张分别写有数字2，4，6，B组的两张分别 写有3，5．它们除了数字外没有任何区别． ‎ ‎(1)随机从A组抽取一张，求抽到数字为2的概率； ‎ ‎(2)随机地分别从A组、B组各抽取一张，请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则：若选出的两数之积为3的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？ ‎ 六、 ‎（本题8分)‎ ‎25.如图，已知反比例函数的图象与一次函数的图象交于点A（1，4）、点B（－4，n）． ‎ ‎(1)求和的值； ‎ ‎(2)求△OAB的面积； ‎ ‎(3)直接写出一次函数值大于反比例函数值的自变量的取值范围． ‎ ‎[来源:学#科#网]‎ 六、 ‎（本题10分)‎ ‎26.某商场购进一批日用品，若按每件5元的价格销售，每月能卖出3万件；若按每件6元的价格销售，每月能卖出2万件，假定每月销售件数（件）与价格（元/件）之间满足一次函数关系．‎ ‎(1)试求：y与x之间的函数关系式；‎ ‎ ‎ ‎[来源:Z.xx.k.Com]‎ ‎（2）若这批日用品购进时进价为4元，则当销售价格定为多少时，才能使每月的 润最大？每月的最大利润是多少？‎ 八、（本题10分）‎ ‎27.如图，已知抛物线与轴、轴分别相交于点A（－1，0）‎ 和B（0，3），其顶点为D． ‎ ‎(1)求这条抛物线的解析式； ‎ ‎(2)若抛物线与轴的另一个交点为E，求△ODE的面积；抛物线的对称轴 上是否存在点P使得△PAB的周长最短．若存在请求出点P的坐标，若不 存在说明理由． ‎ ‎2017.12期末检测九年级数学试题答案 一、 选择 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10[来源:Zxxk.Com]‎ ‎11‎ ‎12‎ D B A D A C C B C B B C 二、填空：‎ 13. ‎ 14. 5 15. y2 < y1 < y3 16 2018 ‎ ‎17. 60° 18. ‎ ‎19.解： 3x（x﹣1）=2x﹣2‎ ‎3x（x﹣1）－2（x﹣1）=0…………1分 ‎（3x－2）（x﹣1）=0…………3分 ‎∴3x－2=0或x﹣1=0，…………5分 解得，，．…………6分 ‎ 20．解：(1)如图，△A1B1C1即为所求．……2分 (2) 如图，△AB2C2即为所求．……2分 点B2(4，－2)，C2(1，－3)．……6分 ‎21.解：(1)∵抛物线经过点（1，-2），‎ ‎ ∴，解得a=-1；……3分 ‎(2)∵函数的对称轴为x=3，‎ ‎∴ A（m，y1）、B（n，y2）（m＜n＜3）在对称轴左侧，‎ 又∵抛物线开口向下，∴ 对称轴左侧y随x的增大而增大，‎ ‎ ∵ m＜n＜3，∴ y1＜y2．……6分 ‎ ‎22..解：设截去的小正方形的边长为xcm，由题意，得 ‎（60﹣2x）（40﹣2x）=800--------------------3分 解得：x1=10，x2=40（不合题意，舍去），---------------5分 答：矩形铁皮的面积是117平方米．-------------6分 ‎23.证明：连接AD，OD，‎ ‎∵AB是直径，∴∠ADB=90°，[来源:学|科|网Z|X|X|K]‎ ‎∵AB=AC，∴BD=DC，‎ ‎∵OB=OA，∴OD 是△ABC的中位线，∴OD∥AC，‎ 又∵DE⊥AC，∴∠AED=90°，∴∠ODE=∠AED=90°‎ ‎∴DE是⊙O的切线．‎ 备注：证法不唯一 24. ‎（1）解：P（抽到数字为2）=1/3-----------------2分 （2）解：不公平，理由如下．画树状图如下： 从树状图中可知共有6个等可能的结果，而所选出的两数之积为3的倍数的机会有4个．‎ ‎---------------5分 ‎ ‎∴P（甲获胜）= ，而P（乙获胜）= ，------------6分 ‎ ‎∵P（甲获胜）＞P（乙获胜） ∴这样的游戏规则对甲乙双方不公平-------------------7分 25. 解：把A点（1，4）分别代入反比例函数y= ，一次函数y=x+b，‎ ‎∴解得k=4, b=3 -------2分 ∵点B（﹣4，n）在直线y=x+3上，‎ ‎∴ n=－1 -------3分 ‎（2）∵直线y=x+3与y轴的交点C坐标为（0，3）， ∴OC=3 ∴S△AOB=S△AOC+S△BOC= = ---------------------------6分 ‎ （3） 根据图象可知：当x＞1或﹣4＜x＜0时，一次函数值大于反比例函数值 ------8分 ‎ ‎ ‎26.解：（1）由题意，可设y=kx+b（k≠0），…………1分 把（5，30000），（6，20000）代入得：，‎ 解得：，…………4分 ‎ 所以y与x之间的关系式为： y=﹣10000x+80000；…………5分 ‎（2）设利润为W元，则W=（x﹣4）（﹣10000x+80000）…………6分 整理得 W=﹣10000（x﹣6）2+40000 …………8分 所以当x=6时，W取得最大值，最大值为40000元．‎ 答：当销售价格定为6元时，每月的利润最大，每月的最大利润为40000元…………10分 ‎27.解：（1）解：根据题意得 ，解得 ， ‎ ‎ ‎ ‎∴抛物线解析式为y=﹣x2+2x+3----------------------3分 ‎ ‎（2）解：当y=0时，﹣x2+2x+3=0，解得x1=﹣1，x2=3，则E（3，0）； --------4分 ‎ ∵抛物线y=﹣（x﹣1）2 + 4的顶点坐标D（1，4）， ∴S△ODE= 1/2×3×4=6；---------6分 连接BE交直线x=1于点P，如图，由对称性知PA=PE， ∴PA+PB=PE+PB=BE， 此时PA+PB的值最小，----------7分 求得直线BE的解析式为 y=﹣x+3 当x=1时，y=﹣x+3=3，----------------9分 ∴点P坐标（1，2） ---------------10分 ‎