2019年全国中考真题分类汇编：与圆有关的综合（次压轴1） 30页

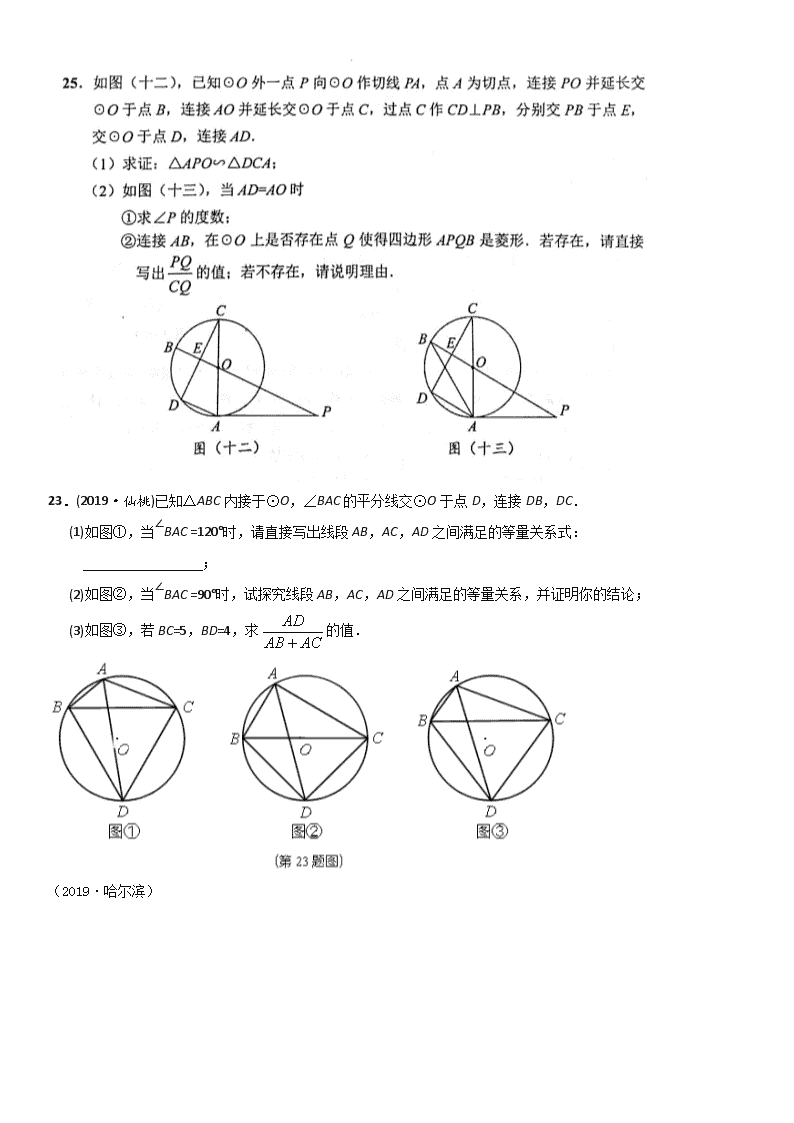
（分类）专题复习（七）与圆有关的综合（次压轴） （2019·内蒙古） （2019·大庆） （2019·柳州） （2019·桂林） （2019·邵阳中考） 23．(2019·仙桃)已知△ABC 内接于⊙O，∠BAC 的平分线交⊙O 于点 D，连接 DB，DC． (1)如图①，当∠BAC =120°时，请直接写出线段 AB，AC，AD 之间满足的等量关系式： ； (2)如图②，当∠BAC =90°时，试探究线段 AB，AC，AD 之间满足的等量关系，并证明你的结论； (3)如图③，若 BC=5，BD=4，求 ACAB AD  的值． （2019·哈尔滨） （2019 河北） (第 22题图) （2019 鄂州）22.(本题满分 10 分)如图，PA 是⊙O 的切线，切点为 A, AC 是⊙O 的直径，连接 OP 交⊙O 于 E.过 A 点作 AB⊥PO 于点 D，交⊙O 于 B，连接 BC，PB. （1）求证：PB 是⊙O 的切线； （2）求证：E为△PAB 的内心； （3）若 cos∠PAB= 10 10 , BC =1，求 PO 的长. （2019 广东）如题 24-1 图,在△ABC 中,AB=AC, 0 是△ABC 的外接圆,过点 C作∠BCD=∠ACB 交 O 于点 D,连接 AD 交 BC 于点 E,延长 DC 至点 F,使 CF=AC,连接 AF (1)求证:ED=EC; (2)求证:AF 是 O 的切线; (3)如题 24-2 图,若点 G 是△ACD 的内心,BC BE=25,求 BG 的长. 解： （2019 深圳） （2019 安顺） （2019 兰州） （2019 苏州）26.(本题满分 10 分) 如图，AB 为⊙O的直径，C 为⊙O 上一点，D是弧 BC 的中点，BC 与 AD、OD 分别交于点 E、F (1)求证:DO//AC；(2)求证: 2DCDADE  ;(3)若 2 1tan CAD ，求 CDAsin 的值 （2019 株洲） （2019 杭州）如图，已知锐角三角形 ABC 内接于圆 O，OD、BC 交于点 D，连接 OA. （1）若∠BAC=60°，①求证：OD= 2 1 OA； ②当 OA=1 时，求△ABC 面积的最大值. （2）点 E 在线段 OA 上，OE=OD，连接 DE，设∠ABC=m∠OED，∠ACB=n∠OED（m,n 是正数），若∠ABC＜∠ACB， 求证： 02  nm . （2019 遂宁） （2019 广安） （2019 淄博） （2019 泰州） 24．（1） DE为⊙O的切线， 理由：连接 OD， ∵AC为⊙O的直径，D为弧 AC的中点， ∴弧 AD=弧 CD, ∴∠AOD＝∠COD＝90°， 又∵DE∥AC， ∴∠EDO＝∠AOD＝90°， ∴DE为⊙O的切线. (2)解：∵DE∥AC， ∴∠EDO＝∠ACD, ∵∠ACD＝∠ABD, ∵∠DCE＝∠BAD, ∴△DCE∽△BAD， ∴ ∵半径为 5，∴AC＝10， ∵ D为弧 AC的中点， ∴AD＝CD＝5 2 ∴ ∴CE＝ （2019 扬州）25.（本题满分 10 分）如图，AB是⊙O的弦，过点 O作 OC⊥OA，OC交于 AB于 P， 且 CP=CB。 （1）求证：BC是⊙O的切线； （2）已知∠BAO=25°，点 Q是弧 AmB上的一点。 ①求∠AQB的度数； ②若 OA=18，求弧 AmB的长。 解（1）连接 OB ∵CP=CB ∴∠CPB=∠CBP ∵OA⊥OC ∴∠AOC=90° ∵OA=OB ∴∠OAB=∠OBA AB DC AD CE  8 25 25  CE 4 25 ∵∠PAO+∠APO=90° ∴∠ABO+∠CBP=90° ∴∠OBC=90° ∴BC是⊙O的切线 （2）①∵∠BAO=25° OA=OB ∴∠BAO=∠OBA=25° ∴∠AOB=130°∴∠AQB=65° ②∵∠AOB=130° OB=18 ∴l 弧AmB=（360°-130°）π×18÷180=23π （2019 滨州）25．（13分）如图，在△ABC中，AB＝AC，以 AB为直径的⊙O分别与 BC，AC交于点 D，E，过点 D作 DF⊥AC，垂足为点 F． （1）求证：直线 DF是⊙O的切线； （2）求证：BC2＝4CF•AC； （3）若⊙O的半径为 4，∠CDF＝15°，求阴影部分的面积． 【分析】（1）如图所示，连接 OD，证明∠CDF+∠ODB＝90°，即可求解； （2）证明△CFD∽△CDA，则 CD2＝CF•AC，即 BC2＝4CF•AC； （3）S 阴影部分＝S 扇形OAE﹣S△OAE即可求解． 【解答】解：（1）如图所示，连接 OD， ∵AB＝AC，∴∠ABC＝∠C，而 OB＝OD，∴∠ODB＝∠ABC＝∠C， ∵DF⊥AC，∴∠CDF+∠C＝90°，∴∠CDF+∠ODB＝90°， ∴∠ODF＝90°， ∴直线 DF是⊙O的切线； （2）连接 AD，则 AD⊥BC，则 AB＝AC， 则 DB＝DC＝ ， ∵∠CDF+∠C＝90°，∠C+∠DAC＝90°，∴∠CDF＝∠DCA， 而∠DFC＝∠ADC＝90°，∴△CFD∽△CDA， ∴CD2＝CF•AC，即 BC2＝4CF•AC； （3）连接 OE， ∵∠CDF＝15°，∠C＝75°，∴∠OAE＝30°＝∠OEA， ∴∠AOE＝120°， S△OAE＝ AE×OEsin∠OEA＝ ×2×OE×cos∠OEA×OEsin∠OEA＝4 ， S 阴影部分＝S 扇形OAE﹣S△OAE＝ ×π×42﹣4 ＝ ﹣4 ． （2019 济宁） （2019 成都） （2019 宜宾） （2019 威海） （2019 巴中） （2019 宁波） （2019·北京）