人教版九年级数学上册专题训练(八)　巧用旋转进行计算与证明 20页

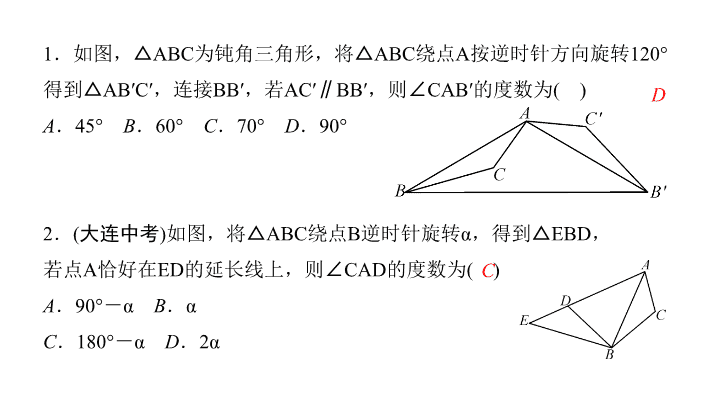
第二十三章　旋转 人教版 专题训练(八)　巧用旋转进行计算与证明 1 ．如图，△ ABC 为钝角三角形，将△ ABC 绕点 A 按逆时针方向旋转 120° 得到△ AB′C′ ，连接 BB′ ，若 AC′∥BB′ ，则∠ CAB′ 的度数为 ( ) A ． 45° B ． 60° C ． 70° D ． 90° 2 ． ( 大连中考 ) 如图，将△ ABC 绕点 B 逆时针旋转 α ，得到△ EBD ， 若点 A 恰好在 ED 的延长线上，则∠ CAD 的度数为 ( ) A ． 90° － α B ． α C ． 180° － α D ． 2α D C 3 ． ( 宁波中考 ) 如图，在△ ABC 中，∠ ACB ＝ 90° ， AC ＝ BC ， D 是 AB 边上一点 ( 点 D 与 A ， B 不重合 ) ，连接 CD ， 将线段 CD 绕点 C 按逆时针方向旋转 90° 得到线段 CE ， 连接 DE 交 BC 于点 F ，连接 BE. (1) 求证：△ ACD≌△BCE ； (2) 当 AD ＝ BF 时，求∠ BEF 的度数． C 5 ． ( 阜新中考 ) 如图，在△ ABC 中， AC ＝ BC ， 将△ ABC 绕点 A 逆时针旋转 60° ，得到△ ADE. 若 AB ＝ 2 ，∠ ACB ＝ 30° ，则线段 CD 的长度为 ____ ． 2 6 ． ( 梧州中考改编 ) 如图，在菱形 ABCD 中， AB ＝ 2 ，∠ BAD ＝ 60° ， 将菱形 ABCD 绕点 A 逆时针方向旋转，对应得到菱形 AEFG ， 点 E 在 AC 上， EF 与 CD 交于点 P. (1) 求线段 AC 的长； (2) 求线段 DP 的长． A A 9 ．如图，△ ABC 为等腰三角形， AB ＝ AC ， D 为△ ABC 内一点， 连接 AD ，将线段 AD 绕点 A 旋转至 AE ，使得∠ DAE ＝∠ BAC ， F ， G ， H 分别为 BC ， CD ， DE 的中点，连接 BD ， CE ， GF ， GH. (1) 求证： GH ＝ GF ； (2) 试说明∠ FGH 与∠ BAC 互补． (2)∵△ABD≌△ACE ，∴∠ ABD ＝∠ ACE ，∵ HG∥CE ， GF∥BD ， ∴∠ HGD ＝∠ ECD ，∠ GFC ＝∠ DBC ， ∴∠ HGD ＝∠ ACD ＋∠ ECA ＝∠ ACD ＋∠ ABD ， ∠ DGF ＝∠ GFC ＋∠ GCF ＝∠ DBC ＋∠ GCF ， ∴∠ FGH ＝∠ DGF ＋∠ HGD ＝∠ DBC ＋∠ GCF ＋∠ ACD ＋∠ ABD ＝ ∠ ABC ＋∠ ACB ＝ 180° －∠ BAC ，∴∠ FGH 与∠ BAC 互补 10 ．如图，在△ ABC 中， AB ＝ AC ， D 是 BC 上一点，且 AD ＝ BD ， 将△ ABD 绕点 A 逆时针旋转得到△ ACE. (1) 求证： AE∥BC ； (2) 连接 DE ，判断四边形 ABDE 的形状，并说明理由 . 解： (1) 证明：由旋转的性质，得∠ BAD ＝∠ CAE ，∵ AD ＝ BD ， ∴∠ B ＝∠ BAD ，∵ AB ＝ AC ，∴∠ B ＝∠ DCA ， ∴∠ CAE ＝∠ DCA ，∴ AE∥BC 　 (2) 四边形 ABDE 是平行四边形．理由：由旋转性质，得 AD ＝ AE ， ∵ AD ＝ BD ，∴ AE ＝ BD ，又∵ AE∥BC ，∴四边形 ABDE 是平行四边形． 11 ． ( 江汉油田中考 ) 问题 ：如图①，在 Rt △ABC 中， AB ＝ AC ， D 为 BC 边上一点 ( 不与点 B ， C 重合 ) ，将线段 AD 绕点 A 逆时针旋转 90° 得到 AE ，连接 EC ，则线段 BC ， DC ， EC 之间满足的等量关系式为 ____________________ ； 探索 ：如图②，在 Rt △ABC 与 Rt △ADE 中， AB ＝ AC ， AD ＝ AE ， 将△ ADE 绕点 A 旋转，使点 D 落在 BC 边上， 试探索线段 AD ， BD ， CD 之间满足的等量关系，并证明你的结论； 应用 ：如图③，在四边形 ABCD 中，∠ ABC ＝∠ ACB ＝∠ ADC ＝ 45°. 若 BD ＝ 9 ， CD ＝ 3 ，求 AD 的长． BC ＝ DC ＋ EC 解： (2)BD 2 ＋ CD 2 ＝ 2AD 2 ，理由如下：连接 CE ，由 (1) ， 得△ BAD≌△CAE ，∴ BD ＝ CE ，∠ ACE ＝∠ B ，∴∠ DCE ＝ 90° ， ∴ CE 2 ＋ CD 2 ＝ ED 2 ，在 Rt △ADE 中， AD 2 ＋ AE 2 ＝ ED 2 ， 又 AD ＝ AE ，∴ BD 2 ＋ CD 2 ＝ 2AD 2