2021中考数学复习微专题 《二次函数图象与一元二次方程 的关系》知识点解读与能力提升练习（无答案） 5页

中考数学微专题《二次函数图象与一元二次方程 )0(02  acbxax 的关系》知识点解读与能力提升练习 一.二次函数图象与一元二次方程 )0(02  acbxax 的关系 一 般 地 ， 二 次 函 数 )0(2  acbxaxy 的 图 象 与 一 元 二 次 方 程 )0(02  acbxax 的根有如下关系： 1.如果二次函数 )0(2  acbxaxy 的图象与 x 轴有两个公共点，那么一元二 次方程 )0(02  acbxax 有两个不相等的实数根； 2.如果二次函数 )0(2  acbxaxy 的图象与 x 轴有且只有一个公共点，那么 一元二次方程 )0(02  acbxax 有两个相等的实数根； 3.如果二次函数 )0(2  acbxaxy 的图象与 x 轴没有公共点，那么一元二次 方程 )0(02  acbxax 没有实数根； 二.二次函数 )0(2  acbxaxy 与一元二次方程 )0(02  acbxax 的关系 acb 42  决定抛物线与 x 轴交点的个数 1. 042  acb 抛物线与 x 轴有两个交点； 2. 042  acb 抛物线与 x 轴只有一个交点； 3. 042  acb 抛物线与 x 轴没有交点。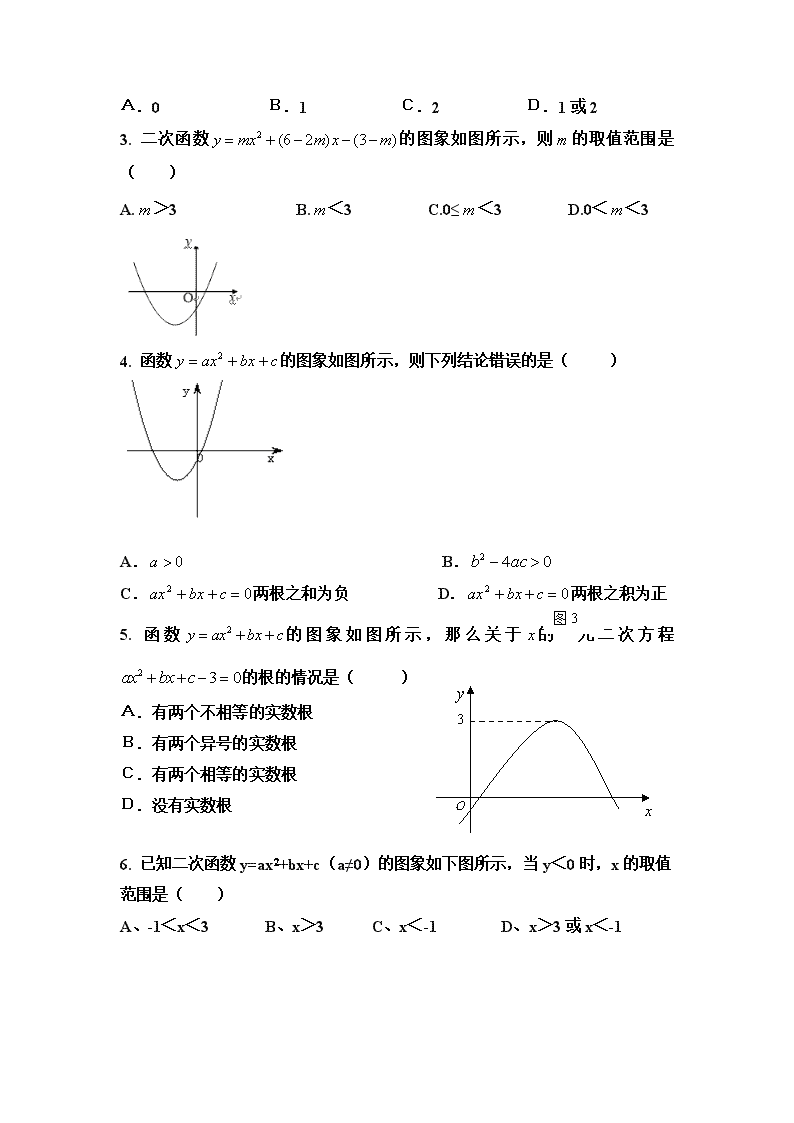 练习反馈： 1. 关于 x 的二次函数 22 (8 1) 8y mx m x m    的图象与 x 轴有交点，则 m 的范围 是（ ） Ａ． 1 16m   Ｂ． 1 16m ≥ 且 0m  Ｃ． 1 16m   Ｄ． 1 16m   且 0m  2. 函数 2 2y mx x m   （ m 是常数）的图象与 x 轴的交点个数为（ ） Ａ．0 Ｂ．1 Ｃ．2 Ｄ．1 或 2 3. 二次函数 2 (6 2 ) (3 )y mx m x m     的图象如图所示，则 m 的取值范围是 （ ） A. m ＞3 B. m ＜3 C.0≤ m ＜3 D.0＜ m ＜3 4. 函数 cbxaxy  2 的图象如图所示，则下列结论错误的是（ ） A． 0a B． 042  acb C． 02  cbxax 两根之和为负 D． 02  cbxax 两根之积为正 5. 函 数 2y ax bx c   的 图 象 如 图 所 示 ， 那 么 关 于 x 的 一 元 二 次 方 程 2 3 0ax bx c    的根的情况是（ ） Ａ．有两个不相等的实数根 Ｂ．有两个异号的实数根 Ｃ．有两个相等的实数根 Ｄ．没有实数根 6. 已知二次函数 y=ax2+bx+c（a≠0）的图象如下图所示，当 y＜0 时，x 的取值 范围是（ ） A、-1＜x＜3 B、x＞3 C、x＜-1 D、x＞3 或 x＜-1 图 3 3 Ｏ x y 7.抛物线 22 8 3y x x   与 x 轴有 个交点，因为其判别式 2 4b ac  0， 相应二次方程 23 2 8 0x x   的根的情况为 ． 8. 关于 x 的方程 2 5mx mx m   有两个相等的实数根，则相应二次函数 2 5y mx mx m    与 x 轴必然相交于 点，此时 m  。 9. 已知二次函数 2 2y x x m    的部分图象如图 所示，则关于 x 的一元二次方 程 2 2 0x x m    的解为＿＿． 10. 如图所示，函数 2( 2) 7 ( 5)y k x x k     的图象与 x 轴只有一个交点，则 交点的横坐标 0x  ． 11. 若抛物线 mxxy  22 与 x 轴的一个交点是（-2，0），则另一个交点坐标 是______。 x y O 1 3 Ｏ y x 12. 已知二次函数 21 2y x bx c    ，关于 x 的一元二次方程 21 02 x bx c    的两个 实根是 1 和 5 ，则这个二次函数的解析式为 . 13.已知抛物线 2xy  和直线 22 )1( mxmy  ，当 m 为何实数时，抛物线与直 线有两个交点？ 14.已知二次函数 142  kxxy （1） 若抛物线与 x 轴有两个不同的交点，求 k 的取值范围。 （2） 若抛物线的顶点在 x 轴上，求 k 的取值。 15.已知函数 2 2y x mx m    ． （1）求证：不论 m 为何实数，此二次函数的图象与 x 轴都有两个不同交点； （2）若函数 y 有最小值 5 4  ，求函数表达式． x y 3 3 2 2 1 1 41 1 2 O 16. 已知关于 x 的二次函数 2 12 2  mmxxy 与 2 22 2  mmxxy ，这两个 二次函数的图象中的一条与 x 轴交于 A、B 两个不同的点。 （1） 试判断哪个二次函数的图象经过 A、B 两点； （2） 若 A 点坐标为 )0,1( ，试求 B 点坐标； （3） 在（2）的条件下，对于经过 A、B 两点的二次函数，当取何值时， y 的 值随 x 值增大而减小？ 17. 已知抛物线 7)1(2 22  kxkxy 与 x 轴有两个不同的交点。 (1)求 k 的范围; (2)若抛物线与 x 轴的交点为 A、B，且点 B 的坐标为（3，0）， 求点 A 的坐标