- 390.50 KB
- 2021-11-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
22.3.1 实际问题与二次函数
一、学习目标:
1、分析实际问题中变量之间的二次函数关系;
2、会运用二次函数求实际问题中的最大值或最小值;
3、能应用二次函数的性质解决图形中最大面积问题.
二、学习重难点:
重点:能应用二次函数的性质解决图形中最大面积问题;
难点:分析实际问题中变量之间的二次函数关系
探究案
三、教学过程
(一)复习巩固
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)y=x2-4x-5; (配方法) (2)y=-x2-3x+4.(公式法)
(二)情境导入
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s
9
)之间的关系式是:().小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
小组内探究分析:
分析:
画出的图象,借助函数图象解决实际问题:
从函数的图象看是一条抛物线的一部分可以看出,抛物线的顶点是这个函数的图象的 点,也就是说,当t取顶点的横坐标时,这个函数有最 值
解:当 = = 时,
h有最大值 = .
∴小球运动的时间是 时,小球运动到最大高度是 .
活动2:探究归纳
一般地,
当a>0(a )时,抛物线 (a≠0)的顶点是最低( )点,也就是说,当x=( ) 时,y有最小( )值是 。
例题解析
例1 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
9
变式训练
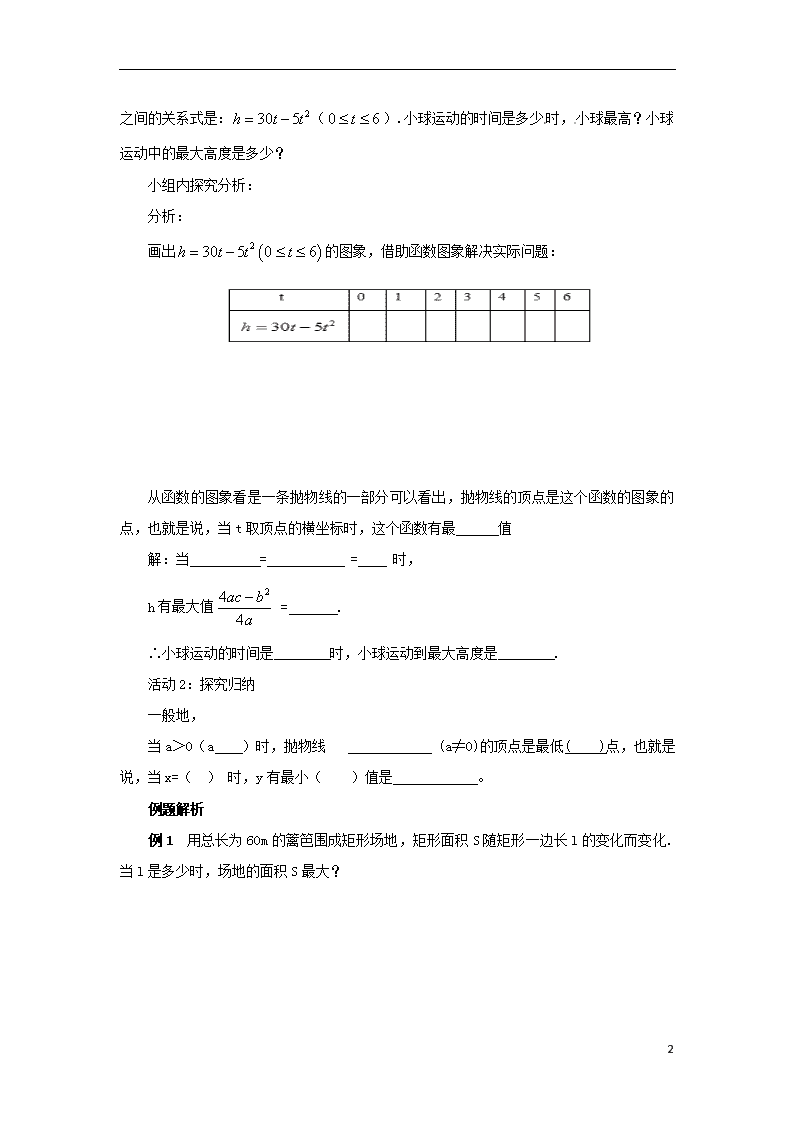
1、如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
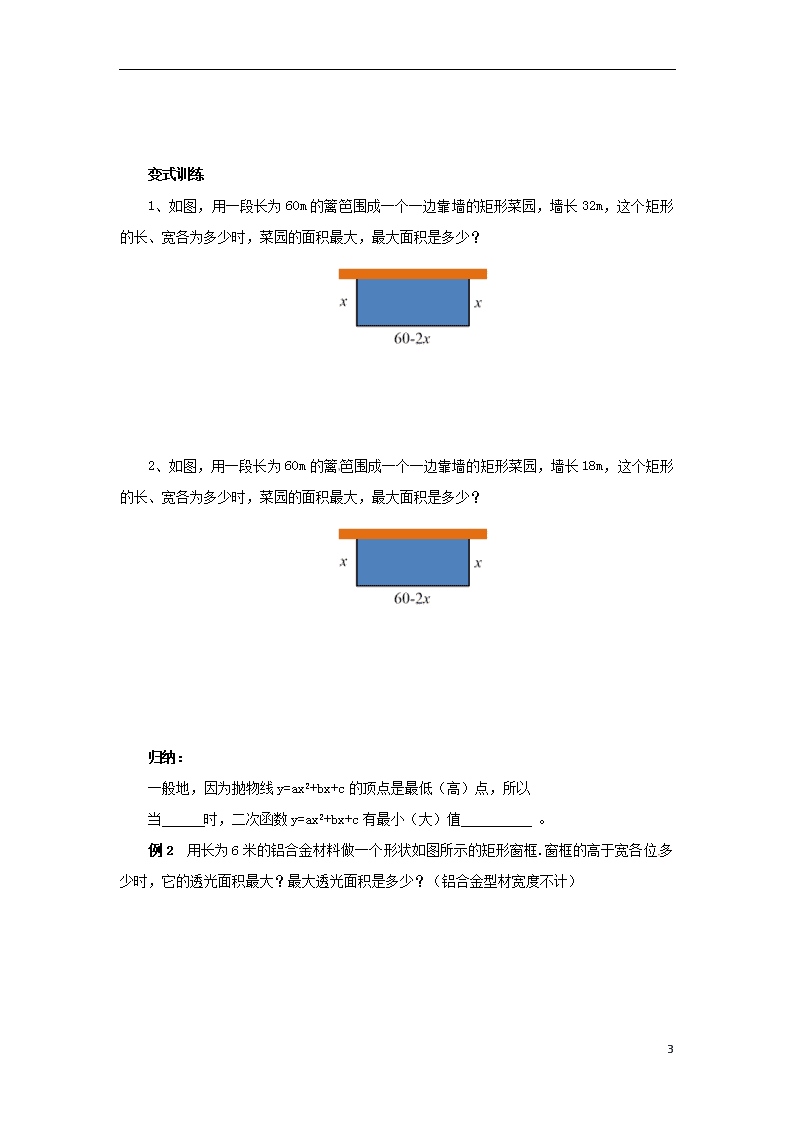
2、如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
归纳:
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以
当 时,二次函数y=ax2+bx+c有最小(大)值 。
例2 用长为6米的铝合金材料做一个形状如图所示的矩形窗框.窗框的高于宽各位多少时,它的透光面积最大?最大透光面积是多少?(铝合金型材宽度不计)
9
随堂检测
1.如图1,用长8m的铝合金条制成如图的矩形窗框,那么最大的透光面积是
2.如图2,在△ABC中, ∠B=90 °,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过______秒,四边形APQC的面积最小.
3.已知直角三角形的两直角边之和为8,两直角边分别为多少时,此三角形的面积最大?最大值是多少?
4. 某小区在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD
9
,绿化带一边靠墙, 另三边用总长为40m的栅栏围住.设绿化带的边长BC为xm,绿化带的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量的取值范围.
(2)当x为何值时,满足条件的绿化带的面积最大?
5. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
课堂小结
通过本节课的学习在小组内谈一谈你的收获,并记录下来:
我的收获
__________________________________
9
________________________________________________________________________________________________________________________
9
参考答案
(一)复习巩固
解:(1)开口方向:向上;对称轴:x=2;顶点坐标:(2,-9);最小值:-9;
(2)开口方向:向下;对称轴:x=;顶点坐标:( , );最大值: .
(二)情境导入
大
3s 45 m
< y = ax 2 + bx + c 高
大
例题解析
例1解:根据题意得S=l(30-l),
即 S=-l2+30l (0
相关文档
- 初中语文2020中考古诗词默写试题汇2021-11-0617页
- 2014年山东省东营市初中学生学业考2021-11-0613页
- 初中语文九年级苏轼和他的词2021-11-0614页
- 初中化学九年级上册周周清检测内容2021-11-064页
- 初中数学中考复习课件章节考点专题2021-11-0614页
- 2008年泉州市实验中学初中化学竞赛2021-11-067页
- 人教版初中物理课后作业课件2第二2021-11-0613页
- 初中道德与法治部编版九年级上册课2021-11-0626页
- 2019年江苏省苏州市初中毕业暨升学2021-11-068页
- 人教版初中九年级化学上学期第三单2021-11-068页