苏科版九年级上数学期中调研试卷（苏教版九年级数学上册期中考试测试卷） 4页

第一学期期中学情分析 九 年 级 数 学 试 卷 一、填空题（每小题 2 分，共 24 分．） １．已知 m n 3 5  ，则 m n m = ． ２．已知 1x  是方程 2 2 0x mx   的一个根，则 m 的值是 ． ３．已知线段 c 是线段 a 、b 的比例中项，且 4a  ， 9b  ，则 c  ． ４．如图，在△ABC 中，DE∥BC， 2 3 AD DB  ，则 DE BC = ． ５. 若关于 x 的一元二次方程 kx2－4x+3=0 有实数根，则 k 的取值范围是 ． ６．已知 1 2,x x 是一元二次方程 2 4 1 0x x   的两个根，则 1 2x x 等于 ． ７. 如图，在□ABCD 中，点 E 是边 AD 的中点，EC 交对角线 BD 于点 F，则 DEF BCF S S   = ． ８．将代数式x2+6x+3 配方成(x+m)2+n 的形式，则 m n = ． ９．若关于 x 的一元二次方程 2 ( 3) 3 0x m x m    的两个实数根分别为－1 和 n ，则 n = ． 10．如图，为测量学校旗杆的高度，小东用长为 3.2m 的竹竿作测量工具，移动竹竿，使竹竿顶端与旗杆顶端 的影子恰好落在地面的同一点，此时，竹竿与这一点相距 8m，与旗杆相距 22m，则旗杆的高为 m． （第 4 题图） （第 7 题图） （第 10 题图） （第 11 题图） 11．如图，线段 CD 两个端点的坐标分别为 C（3，3），D（4，1），以原点 O 为位似中心，在第一象限内将线 段 CD 扩大为原来的两倍，得到线段 AB，则线段 AB 的中点 E 的坐标为 ． 12．若 m，n 是方程 2 2 0x x   的两个实数根，则 2 2m m n  的值为 ． 二、选择题（本大题共有 5 小题，每小题 2 分，共 10 分．） 13．一元二次方程 ( 2) 2x x x   的根是 A．－1 B．0 C．1 和 2 D. －1 和 2 14．已知关于 x 的一元二次方程 2 2 1 0ax x   有两个不相等的实数根，则 a 的取值范围是 A． a ＜－1 B． a ＞1 C． a ＞－1 且 a ≠0 D． a ＜－1 且 a ≠0 15. 下列条件不能判定△ABC 与△DEF 相似的是 A． AB BC AC DE EF DF   B． AB BC DE EF  , A D   C．∠A=∠D，∠B=∠E D． AB BC DE EF  ，∠B=∠E 16．如图，在△ABC 中，D、E 分别是 AB、BC 上的点，且 DE∥AC，若 1 3 BDE DEC S S   ,则 BDE ACD S S   的值等于 A．1∶5 B． 1∶9 C．1∶12 D．1∶16 17．有两个一元二次方程 M： 2 0ax bx c   ；N： 2 0cx bx a   ，其中 0,ac a c  ．下列四个结论中： ①如果方程 M 有两个相等的实数根，那么方程 N 也有两个相等的实数根； ②如果 0ac  ，方程 M、 N 都有两个不相等的实数根； ③如果 2 是方程 M 的一个根，那么 1 2 是方程 N 的一个根； ④如果方程 M 和方程 N 有一个相同的根，那么这个根必是 x=1 正确的个数有 A．4 个 B．3 个 C．2 个 D．1 个 三、解答题（本大题共有 10 题，共 66 分．） 18．解下列方程（本题满分 15 分，每小题 5 分） （1） 122  xx （2） 0)3(2)3( 2  xx （3） 23 4 1 0x x    19．（本题 6 分）如图， 1l ∥ 2l ∥ 3l ，AB=3，BC=5，DF=12，求 DE 和 EF 的长。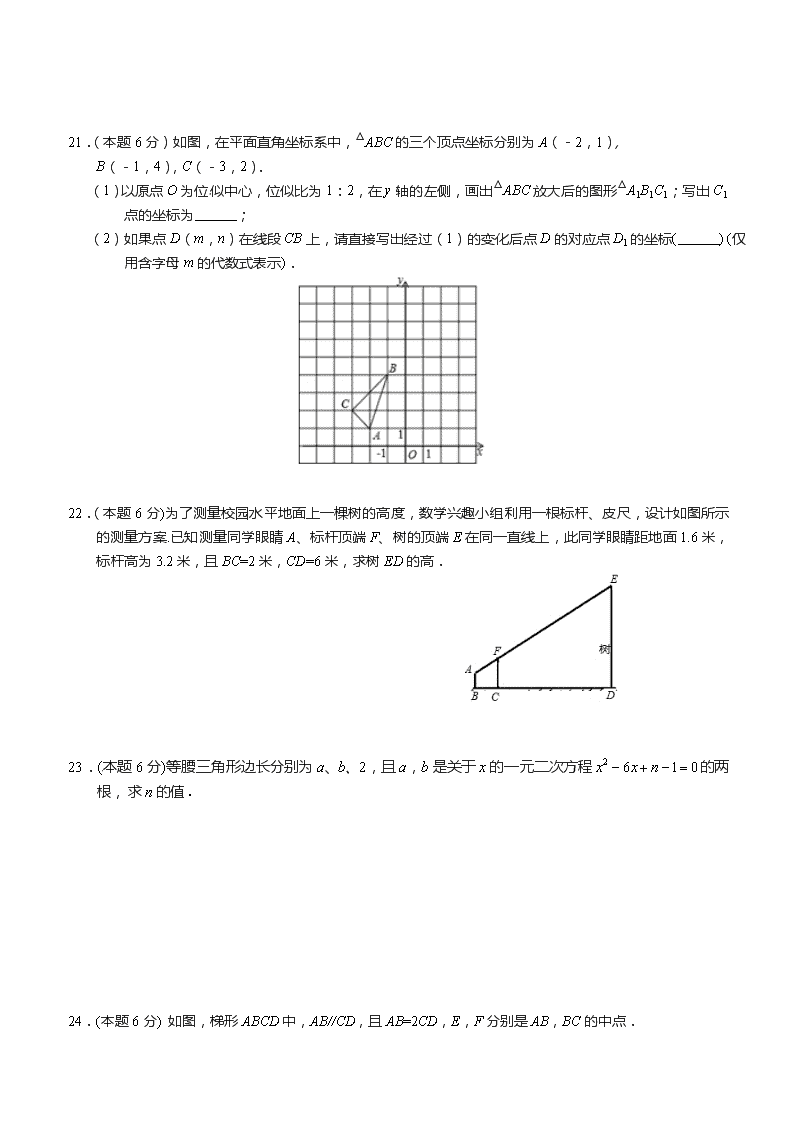 20．（本题 6 分）已知关于 x 的方程 2 2 0x mx m    （1）若该方程的一个根为1，求 m 的值及该方程的另一根； （2）求证：不论 m 取何实数，该方程都有两个不相等的实数根． 21．（本题 6 分）如图，在平面直角坐标系中，△ABC 的三个顶点坐标分别为 A（－2，1）， B（－1，4），C（－3，2）． （1）以原点 O 为位 似中心，位似比为 1：2，在 y 轴的左侧．．，画出△ABC 放大后的图形△A1B1C1；写出 C1 点的坐标为 ； （2）如果点 D（m，n）在线段 CB 上，请直接写出经过（1）的变化后点 D 的对应点 D1 的坐标( ) (仅 用含字母 m 的代数式表示)． 22．（本题 6 分)为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示 的测量方案.已知测量同学眼睛 A、标杆顶端 F、树的顶端 E 在同一直线上，此同学眼睛距地面 1.6 米， 标杆高为 3.2 米，且 BC=2 米，CD=6 米，求树 ED 的高． 23．(本题 6 分)等腰三角形边长分别为 a、b、2，且 a，b 是关于 x 的一元二次方程 2 6 1 0x x n    的两 根，求 n 的值． 24．(本题 6 分) 如图，梯形 ABCD 中，AB//CD，且 AB=2CD，E，F 分别是 AB，BC 的中点． EF 与 BD 相交于点 M． （1）求证：△EDM∽△FBM； （2）若 DB=9，求 BM． 25．（本题 6 分）某校园商店经销甲、乙两种文具． 现有如下信息: 请根据以上信息，解答下列问题： （1）甲、乙两种文具的零售单价分别为 元和 元．（直接写出答案） （2）该校园商店平均每天卖出甲文具 50 件和乙文具 120 件．经调查发现，甲种文具零售单价每降 0.1 元， 甲种文具每天可多销售 10 件．为了降价促销，使学生得到实惠，商店决定把甲种文具的零售单价下 降 m（m＞0）元．在不考虑其他因素的条件下，当m 定为多少时，可以使商店每天销售甲、乙两种 文具获取的利润保持不变？ 26．（本题 9 分） （1）问题：如图 1，在四边形 ABCD 中，点 P 为 AB 上一点，∠DPC=∠A=∠B=90°． 求证：AD·BC=AP·BP． （2）探究：如图 2，在四边形 ABCD 中，点 P 为 AB 上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依 然成立？说明理由． （3）应用：请利用（1）（2）获得的经验解决问题： 如图 3，在△ABD 中，AB=6，AD=BD=5．点 P 以每秒 1 个单位长度的速度，由点 A 出发，沿边 AB 向点 B 运动，且 满足∠DPC=∠A．设点 P 的运动时间为 t（秒），当DC 的长与△ABD 底边上的高相 等时，求 t 的值． 信息 1：甲、乙两种文具的进货单价之和是 3 元； 信息 2：甲文具零售单价比进货单价多 1 元，乙文具 零售单价比进货单价的 2 倍少 1 元． 信息 3：某同学按零售单价购买甲文具 3 件和乙文具 2 件， 共付了 12 元．