2020九年级数学下册 第2章圆周角 6页

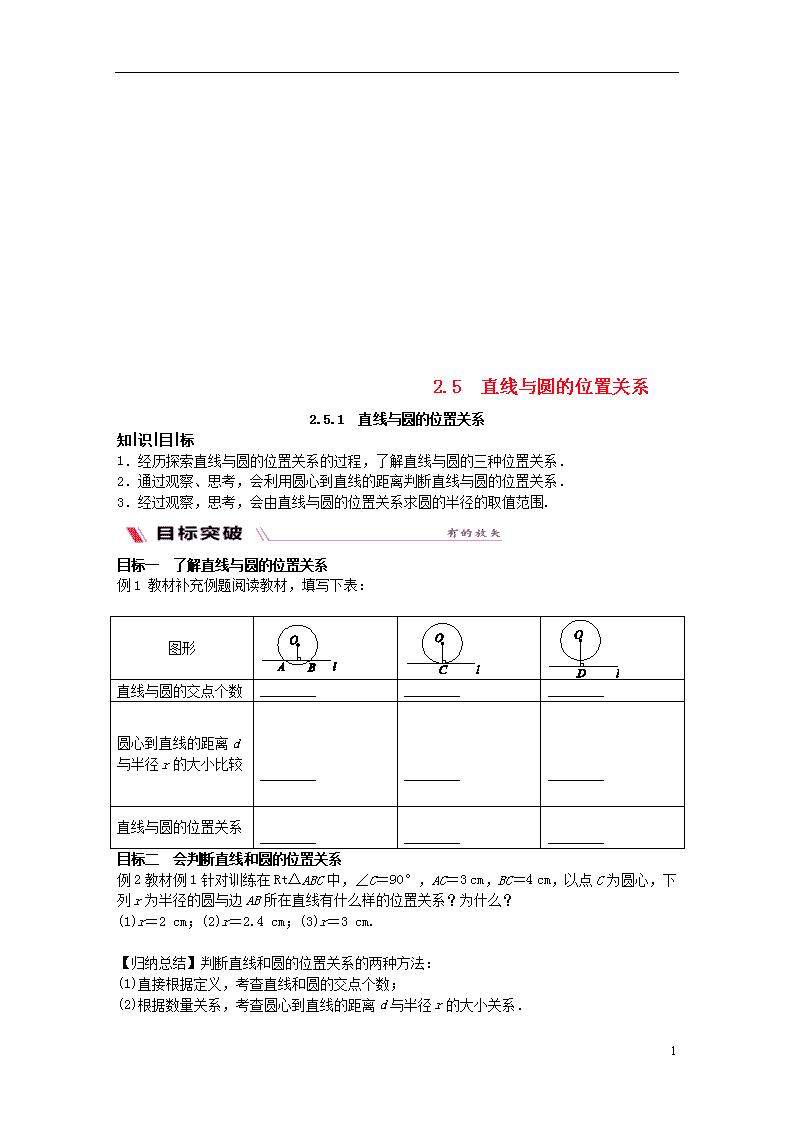
‎2.5　直线与圆的位置关系 ‎2.5.1　‎直线与圆的位置关系 知|识|目|标 ‎1．经历探索直线与圆的位置关系的过程，了解直线与圆的三种位置关系．‎ ‎2．通过观察、思考，会利用圆心到直线的距离判断直线与圆的位置关系．‎ ‎3．经过观察，思考，会由直线与圆的位置关系求圆的半径的取值范围.‎ 目标一　了解直线与圆的位置关系 例1 教材补充例题阅读教材，填写下表：‎ 图形 直线与圆的交点个数 ‎________‎ ‎________‎ ‎________‎ 圆心到直线的距离d与半径r的大小比较 ‎________‎ ‎________‎ ‎________‎ 直线与圆的位置关系 ‎________‎ ‎________‎ ‎________‎ 目标二　会判断直线和圆的位置关系 例2 教材例1针对训练在Rt△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm，以点C为圆心，下列r为半径的圆与边AB所在直线有什么样的位置关系？为什么？‎ ‎(1)r＝‎2 cm；(2)r＝‎2.4 cm；(3)r＝‎3 cm.‎ ‎【归纳总结】判断直线和圆的位置关系的两种方法：‎ ‎(1)直接根据定义，考查直线和圆的交点个数；‎ ‎(2)根据数量关系，考查圆心到直线的距离d与半径r的大小关系．‎ 6‎ 目标三　能由直线与圆的位置关系求半径的取值(范围)‎ 例3 教材补充例题如图2－5－1，在Rt△ABC中，∠C＝90°，AC＝3，AB＝5，若以点C为圆心，r为半径作圆，则：‎ ‎(1)当直线AB与⊙C相切时，求r的值；‎ ‎(2)当直线AB与⊙C相离时，求r的取值范围．‎ 图2－5－1‎ ‎【归纳总结】根据直线和圆的位置关系求圆的半径的取值或取值范围的步骤：‎ ‎(1)过圆心作已知直线的垂线；‎ ‎(2)求出圆心到直线的距离；‎ ‎(3)根据直线与圆的位置关系求出半径的取值或取值范围．‎ 知识点一　直线和圆的位置关系的概念 ‎(1)直线和圆没有公共点，则这条直线和圆______．‎ ‎(2)直线和圆只有一个公共点，则这条直线和圆______，这条直线叫作圆的__________，这个点叫作______．‎ ‎(3)直线和圆有两个公共点，则这条直线和圆______，这条直线叫作圆的______．‎ 知识点二　直线和圆的位置关系 设圆的半径为r，圆心到直线的距离为d.‎ ‎(1)直线和圆相离⇔d____r；‎ ‎(2)直线和圆相切⇔d____r；‎ ‎(3)直线和圆相交⇔d____r.‎ ‎1．已知⊙O的半径为‎2 cm，直线l上有一点P，OP＝‎2 cm，求直线l与⊙O的位置关系．‎ 解：∵OP＝2 cm，⊙O的半径r＝2 cm，①‎ ‎∴OP＝r，②‎ ‎∴圆心O到直线l的距离OP等于圆的半径，③‎ ‎∴直线l与⊙O相切．④‎ 以上推理错在第________步．正确的推理如下：‎ 圆心O到直线l的距离________OP(即圆的半径)，‎ ‎∴直线与⊙O____________．‎ ‎2．在△ABC中，∠C＝90°，AC＝3，BC＝4，如图2－5－2.以点C为圆心，以R为半径画圆，若⊙C与AB边只有一个公共点，求R的取值范围．‎ 6‎ 图2－5－2‎ 解：当⊙C与AB边只有一个公共点时，⊙C与AB边相切，此时R等于点C到AB的距离．‎ 如图2－5－3，过点C作CD⊥AB于点D.‎ 图2－5－3‎ ‎∵AB＝＝5，‎ ‎∴CD＝＝＝，‎ ‎∴R＝.‎ 以上解答是否完整？若不完整，请进行补充．‎ 6‎ 6‎ 教师详解详析 ‎【目标突破】‎ 例1　2　1　0　dr　相交　相切　相离 例2　[解析] 欲判定⊙C与直线AB的位置关系，只需先求出圆心C到直线AB的距离CD的长，然后再与r比较即可．‎ 解： 如图所示，过点C作CD⊥AB于点D.‎ ‎∵∠ACB＝90°，‎ ‎∴AB＝＝5 cm.‎ 又∵AC·BC＝AB·CD，‎ ‎∴CD＝2.4 cm＝d.‎ ‎(1)∵d＝‎2.4 cm＞r＝‎2 cm，‎ ‎∴⊙C与直线AB相离．‎ ‎(2)∵d＝‎2.4 cm＝r，∴⊙C与直线AB相切．‎ ‎(3)∵d＝‎2.4 cm＜r＝‎3 cm，‎ ‎∴⊙C与直线AB相交．‎ ‎[备选例题] 如图所示，在△ABC中，AD为BC边上的高，且AD＝BC，E，F分别为AB，AC的中点，试问以EF为直径的圆与BC有怎样的位置关系？‎ 解： 设EF的中点为O，过点O作OG⊥BC于点G.‎ ‎∵AE＝BE，AF＝CF，‎ ‎∴EF＝BC，‎ 即BC＝2EF.‎ 又∵OG⊥BC，AD⊥BC，AD＝BC，‎ ‎∴OG＝AD＝BC＝×(2EF)＝EF＝OF.‎ ‎∴以EF为直径的圆与BC相切．‎ ‎[归纳总结] 这是一个“探索性”问题．这类问题的特点是问题的结论没有给出，而要根据问题的条件，通过探索得出结论，然后加以说明．‎ 例3　解： (1)过点C作CD⊥AB于点D.‎ ‎∵在Rt△ABC中，AC＝3，AB＝5，‎ 6‎ ‎∴BC＝＝4.‎ ‎∵AC·BC＝AB·CD，∴CD＝d＝2.4.‎ ‎∵当直线AB与⊙C相切时，d＝r，∴r＝2.4.‎ ‎(2)由(1)知，圆心C到直线AB的距离d＝2.4.‎ ‎∵当直线AB与⊙C相离时，d>r，‎ ‎∴03 cm.‎ ‎[归纳总结] 由直线与圆的位置关系可得圆心到直线的距离d与半径r的大小关系．根据这个关系，由d可求出r(或其取值范围)，由r可求出d(或其取值范围)．‎ ‎【总结反思】‎ ‎[小结] 知识点一　(1)相离　(2)相切　切线　切点　(3)相交　割线 知识点二　(1)>　(2)＝　(3)<‎ ‎[反思] 1.③　≤　相交或相切 ‎2．不完整．补充如下：‎ 当3＜R≤4时，⊙C与AB边也只有一个公共点，此时⊙C与直线AB相交，∴R的取值范围是R＝或3＜R≤4.‎ 6‎