四年中考2010-2013全国各地中考数学试题分类汇编汇编 二次函数 230页

2010-2013 全国各地中考数学试题分类汇编 二次函数 2013 全国各地中考数学试题分类汇编 二次函数 一、选择题 1．（2013 江苏扬州，8，3 分）方程 0132  xx 的根可视为函数 3 xy 的图象与函数 xy 1 的图象 交点的横坐标，则方程 3 2 1 0x x   的实根 0x 所在的范围是（ ）． A． 4 10 0  x B． 3 1 4 1 0  x C． 2 1 3 1 0  x D． 12 1 0  x [来源:%@中~&教*网] 【答案】C． 【解析】首先根据题意推断方程 x3＋2x－1=0 的实根是函数 y=x2＋3 与 xy 1 的图象交点的横坐标，再根 据四个选项中 x 的取值代入两函数解析式，找出抛物线的图象在反比例函数上方和反比例函数的图象在抛 物线的上方两个点即可判定推断方程 x3＋2x－1=0 的实根 x0 所在范围． 解：依题意得方程 x3＋2x－1=0 的实根是函数 y=x2＋2 与 xy 1 的图象交点的横坐标，这两个函数的图象 如图所示，它们的交点在第一象限． 当 x= 1 4 时，y=x2＋2=2 1 16 ， 1y x  =4，此时抛物线的图象在反比例函数下方； 当 x= 1 3 时，y=x2＋2=2 1 9 ， 1y x  =3，此时抛物线的图象在反比例函数下方； 当 x= 1 2 时，y=x2＋2=2 1 4 ， 1y x  =2，此时抛物线的图象在反比例函数上方； 当 x=1 时，y=x2＋2=3， 1y x  =1，此时抛物线的图象在反比例函数上方． 所以方程 3 2 1 0x x   的实根 0x 所在的范围是 2 1 3 1 0  x ． 所以应选 C． 【方法指导】此题考查了学生从图象中读取信息的数形结合能力．解决此类识图题，同学们要注意分析其 中的“关键点”，还要善于分析各图象的变化趋势． 【易错警示】不会得出函数解析式，不会观察图象而出错． 2.（2013 江苏苏州，6，3 分）已知二次函数 y＝x2－3x＋m（m 为常数）的图象与 x 轴的一个交点为(1，0)， 则关于 x 的一元二次方程 x2－3x＋m＝0 的两实数根是（ ）． A．x1＝1，x2＝－1 B．x1＝1，x2＝2 C．x1＝1，x2＝0 D．x1＝1，x2＝3 【答案】B． 【解析】∵二次函数 y＝x2－3x＋m 的图象与 x 轴的一个交点为（1，0），∴0＝12－3＋m，解得 m＝2，∴ 二次函数为 y＝x2－3x＋2．设 y＝0，则 x2－3x＋2＝0．解得 x2＝1，x2＝2，这就是一元二次方程 x2－3x＋ m＝0 的两实数根．所以应选 B．[来源:@中教网*&^#] 【方法指导】考查一元二次方程的根、二次函数图象与 x 轴交点的关系．当 b2－4ac≥0 时，二次函数 y＝ ax2+bx+c 的图象与 x 轴的两个交点的横坐标是一元二次方程 ax2+bx+c＝0 的两个根． 【易错警示】因审题不严，容易错选；或因解方程出错而错选． 3.（2013 湖南益阳，7，4 分）抛物线 1)3(2 2  xy 的顶点坐标是（ ） A．(3，1) B．(3，－1) C．(－3，1) D．(－3，－1) 【答案】：A 【解析】抛物线 2( )y a x h k   的顶点是（h，k） 【方法指导】求一个抛物线的顶点可以先把二次函数配方，再得到顶点坐标；也可以利用顶点公式 24( , )2 4 b ac b a a  求顶点坐标。 4. （2013 重庆市(A)，12，4 分）一次函数 y＝ax＋b（a≠0）、二次函数 y＝ax2＋bx 和反比例函数 y＝ k x (k ≠0)在同一直角坐标系中的图象如图所示，A 点的坐标为(－2，0)．则下列结论中，正确的是（ ） [来~源^@:中教&网%] A．b＝2a＋k B．a＝b＋k C．a＞b＞0 D．a＞k＞0 【答案】D． 【解析】∵一次函数与二次函数的图象交点 A 的坐标为（－2，0），∴－2a＋b＝0，∴b＝2a．[来^*源:%zzstep.&com@] 又∵抛物线开口向上，∴a＞0，则 b＞0．而反比例函数图象经过第一、三象限，∴k＞0． ∴2a＋k＞2a，即 b＜2a＋k．故 A 选项错误． 假设 B 选项正确，则将 b＝2a 代入 a＝b＋k，得 a＝2a＋k，a＝－k．又∵a＞0，∴－k＞0，即 k＜0，这与 k＞0 相矛盾，∴a＝b＋k 不成立．故 B 选项错误． 再由 a＞0，b＝2a，知 a，b 两数均是正数，且 a＜b，∴b＞a＞0．故 C 选项错误．[来#源:中教%*&网~] 这样，就只有 D 选项正确．[来源:中#国教^*@育出版网%] 【方法指导】本题考查一次函数、反比例函数、二次函数的图象，属于图象共存型问题．解决这类问题的 关键是熟练掌握这三类函数的图象及性质，能根据图象所在象限的位置准确判断出各系数的符号．上面解 法运用的是排除法，至于 D 为何正确，可由二次函数 y＝ax2＋bx 与反比例函数 y＝ k x (k≠0)的图象，知当 x ＝－ 2 b a ＝－ 2 2 a a ＝－1 时，y＝－k＞－ 2 4 b a ＝－ 24 4 a a ＝－a，即 k＜a．又因为 a＞0，k＞0，所以 a＞k＞0． 【易错警示】二次函数 a、b、c 的符号的确定与函数图象的关系混淆不清． 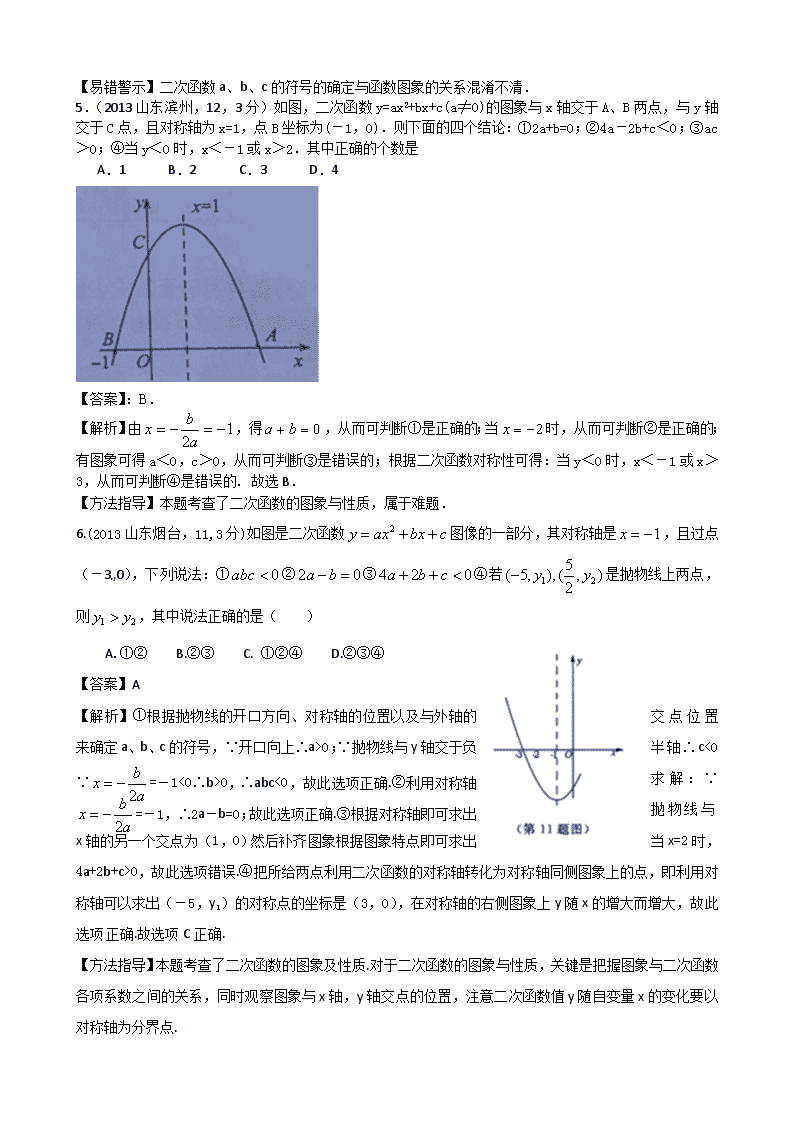5．（2013 山东滨州，12，3 分）如图，二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴交于 A、B 两点，与 y 轴 交于 C 点，且对称轴为 x=1，点 B 坐标为(－1，0)．则下面的四个结论：①2a+b=0；②4a－2b+c＜0；③ac ＞0；④当 y＜0 时，x＜－1 或 x＞2．其中正确的个数是[来源%:z#~z&step@.com] A．1 B．2 C．3 D．4 【答案】：B． 【解析】由 12  a bx ，得 0 ba ，从而可判断①是正确的；当 2x 时，从而可判断②是正确的； 有图象可得 a＜0，c＞0，从而可判断③是错误的；根据二次函数对称性可得：当 y＜0 时，x＜－1 或 x＞3， 从而可判断④是错误的. 故选 B． 【方法指导】本题考查了二次函数的图象与性质，属于难题． 6. (2013 山东烟台，11,3 分)如图是二次函数 cbxaxy  2 图像的一部分，其对称轴是 1x ，且过 点（－3,0），下列说法：① 0abc ② 02 ba ③ 024  cba ④若 ),2 5(),,5( 21 yy 是抛物线上两点， 则 21 yy  ，其中说法正确的是（ ） A.①② B.②③ C. ①②④ D.②③④[来@源:zz#ste&p%.com*] 【答案】A 【解析】①根据抛物线的开口方向、对称轴的位置以及与外轴的交 点 位 置 来 确定 a、b、c 的符号，∵开口向上∴a>0；∵抛物线与 y 轴交于负 半轴∴c<0 ∵ a bx 2  =－1<0∴b>0，∴abc<0，故此选项正确.②利用对称轴 求 解 ： ∵ a bx 2  =－1，∴2a－b=0；故此选项正确.③根据对称轴即可求出 抛物线与 x 轴的另一个交点为（1，0）然后补齐图象根据图象特点即可求出当 x=2 时，4a+2b+c>0，故此选项错误.④ 把所给两点利用二次函数的对称轴转化为对称轴同侧图象上的点，即利用对称轴可以求出（－5，y1）的对 称点的坐标是（3，0），在对称轴的右侧图象上 y 随 x 的增大而增大，故此选项正确.故选项 C 正确.[w~ww.%zzst*@ep.c#om] 【方法指导】本题考查了二次函数的图象及性质.对于二次函数的图象与性质，关键是把握图象与二次函数 各项系数之间的关系，同时观察图象与 x 轴，y 轴交点的位置，注意二次函数值 y 随自变量 x 的变化要以 对称轴为分界点. 对于二次函数 y=ax2+bx+c(a≠0)的图象： （1）开口向上  a>0;开口向下  a<0. （2）c>0  图象与 y 轴的正半轴有交点；c=0  图象过坐标原点； c<0  图象与 y 轴的负半轴有交点； （3）根据对称轴 a bx 2  和 a 符号确定 b 的符号以及 a、b 之间的数量关系. （4）根据 x=1 时 y 的值来确定 a+b+c 的符号；根据 x=－1 时 y 的值来确定 a－b+c 的符号；x=2 时 y 的值来 确定 4a+2b+c 的符号；根据 x=－1 时 y 的值来确定 4a－2b+c 的符号.[来~#源:中国教育出版&% 网^] （5）比较函数值的大小，应根据二次函数的对称性把两个点归纳在对称轴的同侧，然后利用函数的增减 性即可比较大小.[ww&w.~z*zs#tep.co@m] 7. （2013 四川雅安，9，3 分） 将抛物线 y＝ (x －1)2 +3 向左平移 1 个单位，再向下平移 3 个单位后所 得抛物线的解析式为（ ） A．y＝ (x －2)2 B．y＝ (x －2)2 +6 C．y＝x2 +6 D．y＝x2 【答案】D 【解析】抛物线 y＝ (x －1)2 +3 的顶点为（1，3），向左平移 1 个单位，再向下平移 3 个单位后得顶点（0， 0），所以平移后所得抛物线的解析式为 y＝x2．故选 D． 【方法指导】抛物线的平移变换是本题的考查重点，解决此类问题的关键是抓住抛物线顶点坐标的变化． 8. (湖南株洲,8,3 分)二次函数 82 2  mxxy 的图象如图所示，则 m 的值是（ ） A.－8 B.8 C. 8 D.6 6[中国教育*出&@^#版网] 【答案】：C 【解析】:由图可知，抛物线与 x 轴只有一个交点,所以△= 8242 m =0，解得 m=±8.又∵对称轴 022  mx ，∴m＞0，∴m 的值为 8 【方法指导】：本题考查了二次函数图象与 x 轴的交点问题，本题易错点在于要根据对称轴确定出 m 是正 数. 9．（2013 江西南昌，12，3 分）若二次涵数 y=ax+bx+c(a≠0)的图象与 x 轴有两个交点，坐标分别为(x1，0)， (x2，0)，且 x10 B．b2－4ac≥0 C．x10,a<0 两种情况画出两个草图来分析（见下图）. 由图可知 a 的符号不能确定（可正可负，即抛物线的开口可向上，也右向下），所以 0 1 2, ,x x x 的大小就无 法确定；在图 1 中，a>0 且有 1 0 2x x x  ，则 0 1 0 2( )( )a x x x x  的值为负；在图 2 中，a<0 且有 1 0 2x x x  ，则 0 1 0 2( )( )a x x x x  的值也为负.所以正确选项为 D. 【方法指导】本题考查的是二次函数的性质，要求对二次函数的性质有比较深刻地理解，并能熟练地画函 数草图作出分析． 10．（2013 山东德州，8，3 分）下列函数中，当 x>0 时，y 随 x 的增大而增大的是 A、y=－x+1 B、y=x2－1 C、y= x 1 D、y=－x2+1 【答案】B 【解析】A、函数 y=－x+1 ，当 x>0 时，y 随 x 的增大而减小；B、函数 y=x2－1 ，当 x>0（对称轴 y 轴右 侧）时，y 随 x 的增大而增大；C、函数 y= x 1 ，当 x>0（第－象限）时，双曲线一分支 y 随 x 的增大而减 小； D、抛物线 y=－x2+1，当 x>0（对称轴 y 轴右侧）时，y 随 x 的增大而减小. 【方法指导】本题考查一次函数、反比例函数、二次函数图象与性质.解答本题需要了解各函数图象的增 减性特点，解题时不妨画个示意图进行直观判断. 11．（2013 山东德州 ， 11，3 分）函数 y=x2+bx+c 与 y=x 的图象如图所示，有以上结论：①b2－4c>0②b+c+1=0 ③3b+c+6=0④当 1x2+bx+c，即 x2 +(b－1)x+c<0.因此以上说法正确的有③、④. 故选 B.[来源:中%@国#教育出~版网&] 【方法指导】本题考察了二次函数与一次函数的综合应用，解题的关键是联想相关函数与方程、不等式、 坐标交点、图象交点分析，这是解决这类问题的思考点，数形结合思想方法是解题中常用方法. 【易错警示】把握知识点不到位，出现多选或漏选. 12．(2013 山东菏泽，8，3 分)已知 0b  ，二次函数 2 2 1y ax bx a    的图象为下列四个图象之一.试 根据图象分析，的值应等于（ ）[中国&^教育出*%#版网] x y O － 1 x y Ox y Ox y O－ 1 A．﹣2 B．﹣1 C．1 D．2 （题目不清楚）！【答案】C． 【解析】 【方法指导】[来源^:*&@中~教网] 【答案】：C．[中国#教*%育出^版@网] 13．（2013 山东日照，12，4 分）如图,已知抛物线 xxy 42 1  和直线 xy 22  .我们约定：当 x 任取一 值时,x 对应的函数值分别为 y1、y2，若 y1≠y2，取 y1、y2 中的较小值记为 M；若 y1=y2，记 M= y1=y2.[来~源#:中国教育&出版*网%] 下列判断： ①当 x＞2 时，M=y2； ②当 x＜0 时，x 值越大，M 值越大； ③使得 M 大于 4 的 x 值不存在； ④若 M=2，则 x= 1 .其中正确的有 A．1 个 B．2 个 C． 3 个 D．4 个 【答案】B 【解析】当 x＞2 时，M=y1，所以①错误。 当 x＜0 时，两个函数值都是随着 x 的增大而增大的，所以 x 值越 大 ， M 值 越 大，所以②正确。 当 x≤0 时，M=y1 使得 M≤0；当 0＜x≤2，M=y2，使得 M≤4，x＞2 时，M=y1 使得 M≤4.综之，使得 M 大于 4 的 x 值不存在，所以③正确。 当 M=2 时，有两种情况，即，0＜x≤2，M=y2 即得 2x=2,解得 x=1. x＞2 时，M=y1 即得 .(22,22,24- 21 2 舍去）解得  xxxx 所以④错误。 【方法指导】本题是给信息的试题，所以根据题中所给的信息解题即可，但是这种试题要求要把所给的信 息理解透彻。(好恶心的一个点评) 14．（2013 江西，6，3 分）若二次涵数 y=ax2+bx+c(a≠0)的图象与 x 轴有两个交点，坐标分别为(x1，0)，(x2， 0)，且 x10 B．b2－4ac≥0 C．x10,a<0 两种情况画出两个草图来分析（见下图）. [来源:zzst@ep%&^~.com] 由图可知 a 的符号不能确定（可正可负，即抛物线的开口可向上，也右向下），所以 0 1 2, ,x x x 的大小就无 法确定；在图 1 中，a>0 且有 1 0 2x x x  ，则 0 1 0 2( )( )a x x x x  的值为负；在图 2 中，a<0 且有 1 0 2x x x  ，则 0 1 0 2( )( )a x x x x  的值也为负.所以正确选项为 D. 【方法指导】本题考查的是二次函数的性质，要求对二次函数的性质有比较深刻地理解，并能熟练地画函 数草图作出分析． 15．（2013 白银，9，3 分）已知二次函数 y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中： ①2a﹣b＜0；②abc＜0；③a+b+c＜0；④a﹣b+c＞0；⑤4a+2b+c＞0， 错误的个数有（ ） A．1 个 B．2 个 C．3 个 D．4 个 考点：二次函数图象与系数的关系． 分析：由抛物线的开口方向判断 a 与 0 的关系，由抛物线与 y 轴的交点判断 c 与 0 的关系， 利用图象将 x=1，﹣1，2 代入函数解析式判断 y 的值，进而对所得结论进行判断． 解答：解：①∵由函数图象开口向下可知，a＜0，由函数的对称轴 x=﹣ ＜0，故 b＞0， 所以 2a﹣b＜0，①正确； ②∵a＜0，对称轴在 y 轴左侧，a，b 同号，图象与 y 轴交于负半轴，则 c＜0，故 abc ＜0；②正确； ③当 x=1 时，y=a+b+c＜0，③正确； ④当 x=﹣1 时，y=a﹣b+c＜0，④错误； ⑤当 x=2 时，y=4a+2b+c＜0，⑤错误； 故错误的有 2 个． 故选：B． 点评：此题主要考查了图象与二次函数系数之间的关系，将 x=1，﹣1，2 代入函数解析式判 断 y 的值是解题关键． 16．（2013 兰州，3，3 分）二次函数 y=2（x﹣1）2+3 的图象的顶点坐标是（ ） A．（1，3） B．（﹣1，3） C．（1，﹣3） D．（﹣1，﹣3）[来源#~^%:中教网*] 考点：二次函数的性质． 分析：直接根据抛物线的顶点式的特点即可确定顶点坐标． 解答：解：∵y=2（x﹣1）2+3， ∴其顶点坐标是（1，3）． 故选 A． 点评：主要考查了求抛物线的顶点坐标的方法． 17．（2013 兰州，13，3 分）二次函数 y=ax2+bx+c（a≠0）的图象如图所示，则下列说法不正确的是（ ） [来源%:中国教育出版#*~^ 网] A．b2﹣4ac＞0 B．a＞0 C．c＞0 D． [ww~w.#zzst&*e@p.com] 考点：二次函数图象与系数的关系． 分析：由抛物线的开口方向判断 a 与 0 的关系，由抛物线与 y 轴的交点判断 c 与 0 的关系，然后根据对 称轴及抛物线与 x 轴交点情况进行推理，进而对所得结论进行判断． 解答：解：A．正确，∵抛物线与 x 轴有两个交点，∴△=b2﹣4ac＞0； B．正确，∵抛物线开口向上，∴a＞0； C．正确，∵抛物线与 y 轴的交点在 y 轴的正半轴，∴c＞0；[来#@^~&源:中教网][来源:z#zstep%.&~com^] D．错误，∵抛物线的对称轴在 x 的正半轴上，∴﹣ ＞0．[中~国教%@育*出版网&][来源:zz^ste*&p.c~o%m] 故选 D． 点评：主要考查二次函数图象与系数之间的关系，以及二次函数与方程之间的转换，根的判别式的熟 练运用． [来源:zzste^p.%#co&m@] 18．（2013 兰州，15，3 分）如图，动点 P 从点 A 出发，沿线段 AB 运动至点 B 后，立即按原路返回，点 P 在运动过程中速度不变，则以点 B 为圆心，线段 BP 长为半径的圆的面积 S 与点 P 的运动时间 t 的函 数图象大致为（ ）[来源:~中教&#网%@] A． B． C． D． [来源:zz&step%.#co@m~] 考点：动点问题的函数图象．[www.z#z&ste^p~.co@m] 分析：分析动点 P 的运动过程，采用定量分析手段，求出 S 与 t 的函数关系式，根据关系式可以得出结 论． 解答：解：不妨设线段 A B 长度为 1 个单位，点 P 的运动速度为 1 个单位，则：（1）当点 P 在 A→B 段运动时，PB=1﹣t，S=π（1﹣t）2（0≤t＜1）； （2）当点 P 在 B→A 段运动时，PB=t﹣1，S=π（t﹣1）2（1≤t≤2）． 综上，整个运动过程中，S 与 t 的函数关系式为：S=π（t﹣1）2（0≤t≤2），[来源:%中国教@^育#*出版网] 这是一个二次函数，其图象为开口向上的一段抛物线．结合题中各选项，只有 B 符合要求． 故选 B． 点评：本题结合动点问题考查了二次函数的图象．解题过程中求出了函数关系式，这是定量的分析方 法，适用于本题，如果仅仅用定性分析方法则难以作出正确选择． 19．（（2013 贵州毕节，14，3 分）将二次函数 y=x2 的图象向右平移一个单位长度，再向上平移 3 个单位长 度所得的图象解析式为（ ） A．y=（x﹣1）2+3 B．y=（x+1）2+3 C．y=（x﹣1）2﹣3 D．y=（x+1）2﹣3 [来源^:*&中教%网~] 考点：二次函数图象与几何变换． 分析：由二次函数 y=x2 的图象向右平移一个单位长度，再向上平移 3 个单位长度，根据平 移的性质，即可求得所得图象的函数解析式．注意二次函数平移的规律为：左加右减， 上加下减． 解答：解：∵二次函数 y=x2 的图象向右平移一个单位长度，再向上平移 3 个单位长度， ∴所得图象的函数解析式是：y=（x﹣1）2+3． 故选 A． 点评：本题考查的是二次函数的图象与几何变换，熟知“上加下减、左加右减”的原则是解答 此题的关键． 20．（2013 湖南张家界，8，3 分）若正比例函数 y=mx（m≠0），y 随 x 的增大而减小，则它和二次函数 y=mx2+m 的图象大致是（ ） A． B． C． D． [中@国教^育%出版~*网] 考点：二次函数的图象；正比例函数的图象． 3718684 分析：根据正比例函数图象的性质确定 m＜0，则二次函数 y=mx2+m 的图象开口方向向下， 且与 y 轴交于负半轴． 解答：解：∵正比例函数 y=mx（m≠0），y 随 x 的增大而减小， ∴该正比例函数图象经过第一、三象限，且 m＜0． ∴二次函数 y=mx2+m 的图象开口方向向下，且与 y 轴交于负半轴． 综上所述，符合题意的只有 A 选项．[来源:学#科#网 Z#X#X#K] 故选 A． 点评：本题考查了二次函数图象、正比例函数图象．利用正比例函数的性质，推知 m＜0 是 解题的突破口． 21．（2013·聊城，12，3 分）如图，在平面直角坐标系中，抛物线 y＝ 经过平移得到抛物线 y＝ ， 其对称轴与两段抛物线所围成的阴影部分的面积为（ ） A．2 B．4 C．8 D．16 考点：二次函数图象与几何变换．[来源:zzste%p.@~c&*om] 分析：根据抛物线解析式计算出 y＝ 的顶点坐标，过点 C 作 CA⊥y 轴于点 A，根据抛物线的对 称性可知阴影部分的面积等于矩形 ACBO 的面积，然后求解即可．[中#国~教育@*出%版网] 解答：解：过点 C 作 CA⊥y， ∵抛物线 y＝ ＝ （x2－4x）＝ （x2－4x＋4）－2＝ （x－2）2－2，[来^&源:中教网@~%][中国教育&出*^@版网#] ∴顶点坐标为 C（2，－2），对称轴与两段抛物线所围成的阴影部分的面积为：2×2＝4． 点评：本题考查了二次函数的问题，根据二次函数的性质求出平移后的抛物线的对称轴的解析式，并对阴 影部分的面积进行转换是解题的关键． [中~国%教@*育出版网&][来源~%:zz#s*tep.c&om] [中&国教育出版@*~%网] [w#ww.zz@s^te%p~.com] 22．（2013·聊城，8，3 分）二次函数 y＝ax2＋bx 的图象如图所示，那么一次函数 y＝ax＋b 的图象大致 是（ ）[来~#源:中国教育出版^&%网] A． B． C． D． [来~#源:中国教育出版&%网^] 考点：二次函数的图象；一次函数的图象． 专题：数形结合．[来%^~&源#:中教网] 分析：根据二次函数图象的开口方向向下确定出 a＜0，再根据对称轴确定出 b＞0，然后根据一次函数图 象解答即可．[来@源:中国教育出&^*%版网] 解答：解：∵二次函数图象开口方向向下，∴a＜0， ∵对称轴为直线 x＝－ ＞0，[来*@&#源^:中教网]∴b＞0， ∴一次函数 y＝ax＋b 的图象经过第二四象限，且与 y 轴的正半轴相交，[来源&:z*zstep.co@~m%] C 选项图象符合．[来源:%中*国#教~育出^版网] 点评：本题考查了二次函数的图象，一次函数的图象，根据图形确定出 a、b 的正负情况是解题的关键． 23．（2013·泰安，16，3 分）在同一坐标系内，一次函数 y＝ax＋b 与二次函数 y＝ax2＋8x＋b 的图象可 能是（ ） A B C D 考点：二次函数的图象；一次函数的图象． 分析：令 x＝0，求出两个函数图象在 y 轴上相交于同一点，再根据抛物线开口方向向上确定出 a＞0，然 后确定出一次函数图象经过第一三象限，从而得解． 解答：解：x＝0 时，两个函数的函数值 y＝b，所以两个函数图象与 y 轴相交于同一点，故 B、D 选项错误； 由 A、C 选项可知，抛物线开口方向向上，所以 a＞0，所以一次函数 y＝ax＋b 经过第一三象限，所以 A 选项错误，C 选项正确．故选 C．[中~国%&*教育出^版网][中%^@国教&育出~版网] 点评：本题考查了二次函数图象，一次函数的图象，应该熟记一次函数 y＝kx＋b 在不同情况下所在的象 限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等． [来@源:中*&国教%育#出版网] 24（2013·泰安，10，3 分））对于抛物线 y＝－ （x＋1）2＋3，下列结论：①抛物线的开口向下；②对 称轴为直线 x＝1；③顶点坐标为（－1，3）；④x＞1 时，y 随 x 的增大而减小， 其中正确结论的个数为（ ） A．1 B．2 C．3 D．4[来源%:z#~z&step@.com][来~#源*:中&国教育出版网@] 考点：二次函数的性质．[来%&~源^:中@教网] 分析：根据二次函数的性质对各小题分析判断即可得解．[来@源~:中&#教网%] 解答：解：①∵a＝－ ＜0，∴抛物线的开口向下，正确；[中国教育出版&*^网@#] ②对称轴为直线 x＝－1，故本小题错误； ③顶点坐标为（－1，3），正确；[w~ ④∵x＞－1 时，y 随 x 的增大而减小， ∴x＞1 时，y 随 x 的增大而减小一定正确； 综上所述，结论正确的个数是①③④共 3 个．故选 C．[来@源~:中&#教网%] 点评：本题考查了二次函数的性质，主要利用了抛物线的开口方向、对称轴、顶点坐标，以及二次函数的 增减性． [来@源:&zzste^p.com~#] 25（2013•徐州，8，3 分）二次函数 y＝ax2＋bx＋c 图象上部分点的坐标满足下表： x … －3 －2 －1 0 1 … y … －3 －2 －3 －6 －11 … 则该函数图象的顶点坐标为（ ）[来源: A．（－3，－3） B．（－2，－2） C．（－1，－3） D．（0，－6） 考点：二次函数的性质． 分析：根据二次函数的对称性确定出二次函数的对称轴，然后解答即可． 解答：解：∵x＝－3 和－1 时的函数值都是－3 相等， ∴二次函数的对称轴为直线 x＝－2，∴顶点坐标为（－2，－2）．故选 B． 点评： 本题考查了二次函数的性质，主要利用了二次函数的对称性，仔细观察表格数据确定出对称轴是 解题的关键． 26（2013·鞍山，8，2 分）如图所示的抛物线是二次函数 y＝ax2+bx+c（a≠0）的图象，则下列结论：①abc ＞0；②b+2a＝0；③抛物线与 x 轴的另一个交点为（4，0）；④a+c＞b；⑤3a+c＜0． 其中正确的结论有（ ） A．5 个 B．4 个 C．3 个 D．2 个 考点：二次函数图象与系数的关系．[来源:*&~%中^教网] 分析：由开口方向、与 y 轴交于负半轴以及对称轴的位置，即可确定 a，b，c 的正负；由对称轴 x＝－ ＝1，可得 b+2a＝0；由抛物线与 x 轴的一个交点为（－2，0），对称轴为：x＝1，可得抛物线与 x 轴的另 一个交点为（4，0）；当 x＝－1 时，y＝a－b+c＜0；a－b+c＜0，b+2a＝0，即可得 3a+c＜0． 解答：解：∵开口向上，∴a＞0，[来源@:%^中*教网#][中国^*教育#出&@版网] ∵与 y 轴交于负半轴，∴c＜0，[来源^~:&zzstep.c@o%m] ∵对称轴 x＝－ ＞0，[来@#源:~& 中教网%]∴b＜0，[w^w*#w~.zzst@ep.com]∴abc＞0；故①正确； ∵对称轴 x＝－ ＝1，∴b+2a＝0；故②正确； ∵抛物线与 x 轴的一个交点为（－2，0），对称轴为：x＝1， ∴抛物线与 x 轴的另一个交点为（4，0）；故③正确； ∵当 x＝－1 时，y＝a－b+c＜0，∴a+c＜b，故④错误； ∵a－b+c＜0，b+2a＝0，∴3a+c＜0；[来源:@^ 中教&%网#] 故⑤正确．故选 B． 点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用． 27．（2013·济宁，5，3 分）二次函数 y=ax2＋bx＋c（a≠0）的图象如图所示，则下列结论中正确的是（ ） [来源:zzst^ep%.c~om@&] A．a＞0 B．当－1＜x＜3 时，y＞0[来@源:^ 中国教育~% 出版#网] C．c＜0 D．当 x≥1 时，y 随 x 的增大而增大 考点：二次函数图象与系数的关系．[中%&国教*育^出版网~] 分析：由抛物线的开口方向判断 a 与 0 的关系，由抛物线与 y 轴的交点判断 c 与 0 的关系，然后根据对称 轴及抛物线与 x 轴交点情况进行推理，进而对所得结论进行判断．[来源@:zzstep.*%c&#om] 解答：解：A．抛物线的开口方向向下，则 a＜0．故本选项错误；[来^源:&~中#*教网] B．根据图示知，抛物线的对称轴为 x=1，抛物线与 x 轴的一交点的横坐标是－1，则抛物线与 x 轴的另一 交点的横坐标是 3， 所以当－1＜x＜3 时，y＞0．故本选项正确；[www.%zzs@t^e#p*.com] C．根据图示知，该抛物线与 y 轴交与正半轴，则 c＞0．故本选项错误； D．根据图示知，当 x≥1 时，y 随 x 的增大而减小，故本选项错误．[w&ww.z*zste%^p.com~] 故选 B． 点评：本题考查了二次函数图象与系数的关系．二次函数 y=ax2＋bx＋c 系数符号由抛物线开口方向、对称 轴、抛物线与 y 轴的交点抛物线与 x 轴交点的个数确定． [中国教育^&#出*@版网] 28（2013 杭州 3 分）给出下列命题及函数 y=x，y=x2 和 y= ①如果 ，那么 0＜a＜1；②如果 ，那么 a＞1；[中^国教#育出~版&*网] ③如果 ，那么﹣1＜a＜0；④如果 时，那么 a＜﹣1． 则（ ）[中国&教*^育%#出版网] [来源^:&*@中教网%] A．正确的命题是①④ B．错误的命题是②③④ [中国@^*%教育出#版网] C．正确的命题是①② D．错误的命题只有③ 【答案】．A 【解析】易求 x=1 时，三个函数的函数值都是 1，[来源@:&^z%zstep#.com] 所以，交点坐标为（1，1）， 根据对称性，y=x 和 y= 在第三象限的交点坐标为（﹣1，﹣1），[www.%zzs@t&ep#.com*] ①如果 ，那么 0＜a＜1 正确；[来源*:中国教育出&版^@网~] ②如果 ，那么 a＞1 或﹣1＜a＜0，故本小题错误；[来%#源*:中^&教网][来源:*&中国教~育#出版网@] ③如果 ，那么 a 值不存在，故本小题错误； ④如果 时，那么 a＜﹣1 正确． 综上所述，正确的命题是①④．[来~源:zzs^*te%@p.com][中国%&教*育@出~版网] 【方法指导】本题考查了二次函数与不等式组的关系，命题与定理，求出两交点的坐标，并准确识图是解 题的关键． [来源^@:~中国教育出版*网&] 29. 2013•嘉兴 4 分）若一次函数 y=ax+b（a≠0）的图象与 x 轴的交点坐标为（﹣2，0），则抛物线 y=ax2+bx 的对称轴为（ ） A．直线 x=1 B．直线 x=﹣2 C．直线 x=﹣1 D．直线 x=﹣4 【答案】C． 【解析】∵一次函数 y=ax+b（a≠0）的图象与 x 轴的交点坐标为（﹣2，0），[来@源:中国教育*出#%版网&] ∴﹣2a+b=0，即 b=2a， ∴抛物线 y=ax2+bx 的对称轴为直线 x=﹣ =﹣1． 【方法指导】本题考查了一次函数图象上点的坐标特征及二次函数的性质，难度适中．用到的知识点：点 在函数的图象上，则点的坐标满足函数的解析式；[中国教育出版&网^*%#] 二次函数 y=ax2+bx+c 的对称轴为直线 x=﹣ ． 30.( 2013•衢州 3 分）抛物线 y=x2+bx+c 的图象先向右平移 2 个单位，再向下平移 3 个单位，所得图象的函 数解析式为 y=（x﹣1）2﹣4，则 b、c 的值为（ ） A．b=2，c=﹣6 B．b=2，c=0 C．b=﹣6，c=8 D．b=﹣6，c=2 【答案】B． 【解析】函数 y=（x﹣1）2﹣4 的顶点坐标为（1，﹣4）， ∵是向右平移 2 个单位，再向下平移 3 个单位得到， ∴1﹣2=﹣1，﹣4+3=﹣1， ∴平移前的抛物线的顶点坐标为（﹣1，﹣1）， ∴平移前的抛物线为 y=（x+1）2﹣1， 即 y=x2+2x， ∴b=2，c=0． 【方法指导】本题考查了二次函数图象与几何变换，熟练掌握平移的规律：左加右减，上加下减，利用顶 点的变化确定函数解析式可 以使计算更加简便．[来^源:中国%教育出~版网#*] 21.（2013 上海市，3，4 分）如果将抛物线 2 2y x  向下平移 1 个单位，那么所得新抛物线的表 达式是（ ） （A） 2( 1) 2y x   ；（B） 2( 1) 2y x   ； （C） 2 1y x  ；（D） 2 3y x  ． [来源:中国~*教育&^出版@网] 31.（2013 陕西，10，3 分）已知两点 ),3(),,5( 21 yByA  均在抛物线 )0(2  acbcaxy 上，点 ),( 00 yxC 是该抛物线的顶点，若 021 yyy  ，则 0x 的取值范围是（ ） A． 50 x B． 10 x C． 15 0  x D． 32 0  x 考点：二次函数图象性质的应用及对称性的考查。 解析：由点 ),( 00 yxC 是该抛物线的顶点，且 021 yyy  ，所以 0y 为函数的最小值，即得出抛物线的开 口向上，因为 021 yyy  ，所以得出点 A、B 可能在对称轴的两侧或者是在对称轴的左侧，当在对称轴 的左侧时，y 随 x 的增大而减小，因此 0x >3，当在对称轴的两侧时，点 B 距离对称轴的距离小于点 A 到对 称轴的距离，即得 0x -（-5）>3- 0x ,解得 10 x ，综上所得： 10 x ，故选 B 23.（2013 四川巴中，10，3 分）已知二次函数 y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的 是（ ）[来源:&@中国教育出^%*版网] [中国#教~^@育%出版网][中国*教&^育%#出版网] A．ac＞0 B．当 x＞1 时，y 随 x 的增大而减小 C．b﹣2a=0 D．x=3 是关于 x 的方程 ax2+bx+c=0（a≠0）的一个根 考点：二次函数图象与系数的关系；二次函数的性质． 245761 分析：由函数图象可得抛物线开口向上，得到 a 大于 0，又抛物线与 y 轴的交点在 y 轴负半 轴，得到 c 小于 0，进而得到 a 与 c 异号，根据两数相乘积为负得到 ac 小于 0，选项 A 错误； 由抛物线开口向上，对称轴为直线 x=1，得到对称轴右边 y 随 x 的增大而增大，选项 B 错误； 由抛物线的对称轴为 x=1，利用对称轴公式得到 2a+b=0，选项 C 错误； 由抛物线与 x 轴的交点为（﹣1，0）及对称轴为 x=1，利用对称性得到抛物线与 x 轴 另一个交点为（3，0），进而得到方程 ax2+bx+c=0 的有一个根为 3，选项 D 正确． 解答：解：由二次函数 y=ax2+bx+c 的图象可得：抛物线开口向上，即 a＞0， 抛物线与 y 轴的交点在 y 轴负半轴，即 c＜0， ∴ac＜0，选项 A 错误； 由函数图象可得：当 x＜1 时，y 随 x 的增大而减小； 当 x＞1 时，y 随 x 的增大而增大，选项 B 错误； ∵对称轴为直线 x=1，∴﹣ =1，即 2a+b=0，选项 C 错误； 由图象可得抛物线与 x 轴的一个交点为（﹣1，0），又对称轴为直线 x=1， ∴抛物线与 x 轴的另一个交点为（3，0）， 则 x=3 是方程 ax2+bx+c=0 的一个根，选项 D 正确． 故选 D． 点评：此题考查了二次函数图象与系数的关系，以及抛物线与 x 轴的交点，难度适中．二次 函数 y=ax2+bx+c=0（a≠0），a 的符合由抛物线的开口方向决定，c 的符合由抛物线与 y 轴交点的位置确定，b 的符号由 a 及对称轴的位置决定，抛物线的增减性由对称轴 决定，当抛物线开口向上时，对称轴左边 y 随 x 的增大而减小，对称轴右边 y 随 x 的 增大而增大；当抛物线开口向下时，对称轴左边 y 随 x 的增大而增大，对称轴右边 y 随 x 的增大而减小．此外抛物线解析式中 y=0 得到一元二次方程的解即为抛物线与 x 轴交点的横坐标． 32（2013 四川内江，9，3 分）若抛物线 y=x2﹣2x+c 与 y 轴的交点为（0，﹣3），则下列说法不正确的 是（ ） A．抛物线开口向上 B．抛物线的对称轴是 x=1 C．当 x=1 时，y 的最大值为﹣4 D．抛物线与 x 轴的交点为（﹣1，0），（3，0） 考点：二次函数的性质． 分析：A 根据二次函数二次项的系数的正负确定抛物线的开口方向． B 利用 x=﹣ 可以求出抛物线的对称轴． C 利用顶点坐标和抛物线的开口方向确定抛物线的最大值或最小值． D 当 y=0 时求出抛物线与 x 轴的交点坐标． 解答：解：∵抛物线过点（0，﹣3）， ∴抛物线的解析式为：y=x2﹣2x﹣3． A、抛物线的二次项系数为 1＞0，抛物线的开口向上，正确． B、根据抛物线的对称轴 x=﹣ =﹣ =1，正确． C、由 A 知抛物线的开口向上，二次函数有最小值，当 x=1 时，y 的最小值为﹣4，而 不是最大值．故本选项错误． D、当 y=0 时，有 x2﹣2x﹣3=0，解得：x1=﹣1，x2=3，抛物线与 x 轴的交点坐标为（﹣ 1，0），（3，0）．正确． 故选 C． 点评：本题考查的是二次函数的性质，根据 a 的正负确定抛物线的开口方向，利用顶点坐标 公式求出抛物线的对称轴和顶点坐标，确定抛物线的最大值或最小值，当 y=0 时求出 抛物线与 x 轴的交点坐标． 33．（2013 贵州省黔东南州，8，4 分）二次函数 y=ax2+bx+c 的图象如图所示，则下列结论正确的是（ ） A．a＜0，b＜0，c＞0，b2﹣4ac＞0 B．a＞0，b＜0，c＞0，b2﹣4ac＜0 C．a＜0，b＞0，c＜0，b2﹣4ac＞0 D．a＜0，b＞0，c＞0，b2﹣4ac＞0 考点：二次函数图象与系数的关系． 3718684 分析：由抛物线的开口方向判断 a 与 0 的关系，再结合抛物线的对称轴与 y 轴的关系判断 b 与 0 的关系，由抛物线与 y 轴的交点判断 c 与 0 的关系，根据抛物线与 x 轴交点的个 数判断 b2﹣4ac 与 0 的关系． 解答：解：∵抛物线的开口向下， ∴a＜0， ∵对称轴在 y 轴右边， ∴a，b 异号即 b＞0， ∵抛物线与 y 轴的交点在正半轴， ∴c＞0， ∵抛物线与 x 轴有 2 个交点， ∴b2﹣4ac＞0． 故选 D． 点评：二次函数 y=ax2+bx+c 系数符号的确定： （1）a 由抛物线开口方向确定：开口方向向上，则 a＞0；否则 a＜0． （2）b 由对称轴和 a 的符号确定：由对称轴公式 x= 判断符号． （3）c 由抛物线与 y 轴的交点确定：交点在 y 轴正半轴，则 c＞0；否则 c＜0． （4）b2﹣4ac 由抛物线与 x 轴交点的个数确定：2 个交点，b2﹣4ac＞0；1 个交点，b2 ﹣4ac=0；没有交点，b2﹣4ac＜0． [来源:%中@国教~育#出&版网] 34（2013 贵州省黔西南州，10，4 分）如图所示，二次函数 y=ax2+bx+c 的图象中，王刚同学观察得出了 下面四条信息：（1）b2﹣4ac＞0；（2）c＞1；（3）2a﹣b＜0；（4）a+b+c＜0，其中错误的有（ ）[来源:%&中@~教网*] A．1 个 B．2 个 C．3 个 D．4 个 考点：二次函数图象与系数的关系． 分析：由抛物线的开口方向判断 a 与 0 的关系，由抛物线与 y 轴的交点判断 c 与 0 的关系， 然后根据对称轴及抛物线与 x 轴交点情况进行推理，进而对所得结论进行判断． 解答：解：（1）图象与 x 轴有 2 个交点，依据根的判别式可知 b2﹣4ac＞0，正确； （2）图象与 y 轴的交点在 1 的下方，所以 c＜1，错误； （3）∵对称轴在﹣1 的右边，∴﹣ ＞﹣1，又 a＜0，∴2a﹣b＜0，正确； （4）当 x=1 时，y=a+b+c＜0，正确； 故错误的有 1 个． 故选：A． 点评：本题主要考查二次函数图象与系数之间的关系，会利用对称轴的范围求 2a 与 b 的关 系，以及二次函数与方程之间的转换，根的判别式的熟练运用． 35.（2013 河 南 省 ，8，3 分）在二次函数 2 2 1y x x    的图像中，若 y 随 x 的增大而增大，则 x 的取 值范围是（ ） （A） 1x  （B） 1x  （C） 1x   （D） 1x   【解析】二次函数 2 2 1y x x    的开口向下，所以在对称轴的左侧 y 随 x 的增大而增大，二次函数 2 2 1y x x    的对称轴是 2 12 2 ( 1) bx a       ，所以， 1x  [来源%#:@*中教网&] 【答案】A 36．（2013 黑 龙 江 省 哈 尔 滨 市 ，5）把抛物线 y=(x+1)2 向下平移 2 个单位，再向右平移 1 个单位，所 得到的抛物线是( )．[来源:~中教&%*网^] [来%源#:zz@step.*com&] (A)y=(x+2)2+2 (B)y=(x+2)2-2 (C)y=x2+2 (D)y=x2-2[www.z@#%z&st*ep.com] 考点：抛物线的平移 分析：根据平移概念，图形平移变换，图形上每一点移动规律都是一样的，也可用抛物线顶点移动.即（-1， 0）—→（0，－2）.[中国^教#育~出&版%网] 解答：根据点的坐标是平面直角坐标系中的平移规律：“左加右减，上加下减.”故选 D． 37（2013 湖北省鄂州市，9，3 分）小轩从如图所示的二次函数 y=ax2+bx+c（a≠0）的图象中，观察得出了 下面五条信息： ①ab＞0；②a+b+c＜0；③b+2c＞0；④a﹣2b+4c＞0；⑤ ． 你认为其中正确信息的个数有（ ）[中国教@^*%育出#版网] [来*%源:#zzstep&.c^om][来源#:中教网@~%^] [来源:学&科 &网 Z&X&X&K] A．2 个 B．3 个 C．4 个 D．5 个 [www#.zz*^ste&p.co@m] 考点：二次函数图象与系数的关系． 3718684 分析：由抛物线的开口方向判断 a 与 0 的关系，由抛物线与 y 轴的交点判断 c 与 0 的关系， 然后根据对称轴及抛物线与 x 轴交点情况进行推理，进而对所得结论进行判断． 解答：解：①如图，∵抛物线开口方向向下，∴a＜0． ∵对称轴 x=﹣ =﹣ ，∴b= a＜0， ∴ab＞0．故①正确； ②如图，当 x=1 时，y＜0，即 a+b+c＜0． 故②正确； ③如图，当 x=﹣1 时，y=a﹣b+c＞0， ∴2a﹣2b+2c＞0，即 3b﹣2b+2c＞0， ∴b+2c＞0． 故③正确； ④如图，当 x=﹣1 时，y＞0，即 a﹣b+c＞0． 抛物线与 y 轴交于正半轴，则 c＞0． ∵b＜0， ∴c﹣b＞0， ∴（a﹣b+c）+（c﹣b）+2c＞0，即 a﹣2b+4c＞0． 故④正确； ⑤如图，对称轴 x=﹣ =﹣ ，则 ．故⑤正确． 综上所述，正确的结论是①②③④⑤，共 5 个． 故选 D． 点评：本题考查了二次函数图象与系数的关系．二次函数 y=ax2+bx+c 系数符号由抛物线开 口方向、对称轴、抛物线与 y 轴的交点抛物线与 x 轴交点的个数确定． 38．（2013 湖北省十堰市，1，3 分）如图，二次函数 y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过 点（0，1）和（﹣1，0）．下列结论：①ab＜0，②b2＞4a，③0＜a+b+c＜2，④0＜b＜1，⑤当 x＞﹣1 时，y＞0，其中正确结论的个数是（ ） A．5 个 B．4 个 C．3 个 D．2 个 考点：二次函数图象与系数的关系． 3718684 分析：由抛物线的对称轴在 y 轴右侧，可以判定 a、b 异号，由此确定①正确； 由抛物线与 x 轴有两个交点得到 b2﹣4ac＞0，又抛物线过点（0，1），得出 c=1，由此 判定②正确； 由抛物线过点（﹣1，0），得出 a﹣b+c=0，即 a=b﹣1，由 a＜0 得出 b＜1；由 a＜0， 及 ab＜0，得出 b＞0，由此判定④正确； 由 a﹣b+c=0，及 b＞0 得出 a+b+c=2b＞0；由 b＜1，c=1，a＜0，得出 a+b+c＜a+1+1 ＜2，由此判定③正确； 由图象可知，当自变量 x 的取值范围在一元二次方程 ax2+bx+c=0 的两个根之间时， 函数值 y＞0，由此判定⑤错误． 解答：解：∵二次函数 y=ax2+bx+c（a≠0）过点（0，1）和（﹣1，0）， ∴c=1，a﹣b+c=0． ①∵抛物线的对称轴在 y 轴右侧，∴x=﹣ ＞0， ∴a 与 b 异号，∴ab＜0，正确； ②∵抛物线与 x 轴有两个不同的交点，∴b2﹣4ac＞0， ∵c=1，∴b2﹣4a＞0，b2＞4a，正确； ④∵抛物线开口向下，∴a＜0， ∵ab＜0，∴b＞0． ∵a﹣b+c=0，c=1，∴a=b﹣1， ∵a＜0，∴b﹣1＜0，b＜1， ∴0＜b＜1，正确； ③∵a﹣b+c=0，∴a+c=b， ∴a+b+c=2b＞0． ∵b＜1，c=1，a＜0， ∴a+b+c=a+b+1＜a+1+1=a+2＜0+2=2， ∴0＜a+b+c＜2，正确； ⑤抛物线 y=ax2+bx+c 与 x 轴的一个交点为（﹣1，0），设另一个交点为（x，0），则 x0＞0， 由图可知，当 x0＞x＞﹣1 时，y＞0，错误； 综上所述，正确的结论有①②③④． 故选 B． 点评：本题主要考查二次函数图象与系数之间的关系，不等式的性质，难度适中．二次函数 y=ax2+bx+c（a≠0），a 的符号由抛物线开口方向决定；b 的符号由对称轴的位置及 a 的符号决定；c 的符号由抛物线与 y 轴交点的位置决定；抛物线与 x 轴的交点个数， 决定了 b2﹣4ac 的符号，此外还要注意二次函数与方程之间的转换． [来源:zzs&%tep#*.c~om] 二、填空题 1．(2013 湖北荆门，17，3 分)若抛物线 y＝x2＋bx＋c 与 x 轴只有一个交点，且过点 A(m，n)，B(m＋6，n)， 则 n＝______． 【答案】9． 【解析】∵抛物线 y＝x2＋bx＋c 与 x 轴只有一个交点，∴原抛物线的顶点在 x 轴上．将原抛物线的顶点平 移至原点，则所得抛物线的解析式为 y＝x2，且它经过点 A′(－3，n)，B′(3，n)．当 x＝±3 时，n＝(±3)2＝ 9． 【方法指导】此题另一解法如下：依题意，得 m2＋bm＋c＝n①，(m＋6)2＋b(m＋6)＋c＝n②．②－①，得 12m＋36＋6b＝0．即b＝－2(m＋3)．∵抛物线y＝x2＋bx＋c与x 轴只有一个交点，∴b2－4c＝0．即c＝ 2 4 b ．∴ n＝m2＋bm＋c＝m2－2(m＋3)m＋ 1 4 ×4(m＋3)2＝9． 2．（2013 广东湛江，14，4 分）抛物线 2 1y x  的最小值是 ． 【答案】1. 【解析】 2 1y x  的顶点坐标为（0，1）由于抛物线的开口向上，所以它的有最小值 1. 【方法指导】求二次函数 2y ax bx c   的最小值的步骤： 1.把 2y ax bx c   配成顶点式： 2 2 4( )2 4 b ac by a x a a    2.如果 0a  ，当 2 bx a   时，y 有最小值 24 4 ac b a  如果 0a  ，当 2 bx a   时，y 有最大值 24 4 ac b a  3.如果自变量有一定的限制，还得根据图象的性质，确定端点的函数值是否为最 3．(2013 四川成都，24，4 分)在平面直角坐标系 xoy 中，直线 y＝kx(k 为常数)与抛物线 y＝ 1 3 x2－2 交于 A， B 两点，且 A 点在 y 轴左侧，P 点的坐标为(0，－4)，连接 PA，PB．有以下说法：①PO2＝PA·PB；②当 k ＞0 时，(PA＋AO)(PB－BO)的值随 k 的增大而增大；③当 k＝－ 3 3 时，BP2＝BO·BA；④△PAB 面积的最 小值为 4 6 ． 其中正确的是______．(写出所有正确说法的序号) 【答案】③、④． 【解析】由方程组 2 , 1 23 y kx y x    消去 y 得， 1 3 x2－2＝kx．即 x2－3kx－6＝0．(※) 设点 A(x1，kx1)，B(x2，kx2)，其中 x1＜x2，则由(※)方程得 x1＋x2＝3k，x1x2＝－6． ①由勾股定理得 PA＝ 2 2 1 1( 4)x kx  ＝ 2 2 1 1(1 ) 8( 2)k x kx   ． ∵点 A(x1，kx1)在抛物线 y＝ 1 3 x2－2 上，∴kx1＝ 1 3 x12－2． 即 kx1＋2＝ 1 3 x12． ∴PA＝ 2 2 2 1 1 8(1 ) 3k x x  ＝－x1 2 11 3k  ． 同理 PB＝x2 2 11 3k  ． ∴PA·PB＝－x1x2(k2＋11 3 )＝6(k2＋ 11 3 )≥6× 11 3 ＝22． ∴PA·PB≠16．而 PO2＝16，∴PA·PB≠PO2． ∴说法①是错误的． ②由勾股定理得 OA＝ 2 2 1 1( )x kx ＝－x1 21 k ．同理，OB＝x2 21 k ． ∴(PA＋AO)(PB－BO)＝－x1( 2 11 3k  ＋ 21 k )·x2( 2 11 3k  － 21 k ) ＝－x1x2[( 2 11 3k  )2－( 21 k )2]＝6× 8 3 ＝16． 可见当 k 增大时，(PA＋AO)(PB－BO)的值保持不变， ∴说法②是错误的． ③当 k＝－ 3 3 时，如图 4，(※)方程变为 x2＋ 3 x－6＝0． 解得 x1＝ 3 ，x2＝－2 3 ．于是 y1＝－1，y2＝2． 即点 A(－2 3 ，2)，B( 3 ，－1)． 于是求得 PB＝2 3 ，BO＝2，OA＝4，BA＝6． ∵PB2＝(2 3 )2＝12＝2×6，∴BP2＝BO·BA． x y O P A B 图 4 ∴说法③是正确的．[w#ww.&zz~*st%ep.com] ④∵S△PAB＝ 1 2 (x2－x1)·PO＝2 29 24k  ． ∴当 k＝0 时(此时直线 y＝kx 是横轴)，S△PAB 有最小值，最小值＝2 24 ＝4 6 ． ∴说法④是正确的．[ww~w.z%^zst&ep.c@om] 【方法指导】此题难度较大．判断说法①、②时，可先估计它们是错误的，然后分别列举反例进行说明． 4．（2013 兰州，20，4 分）如图，以扇形 OAB 的顶点 O 为原点，半径 OB 所在的直线为 x 轴，建立平面 直角坐标系，点 B 的坐标为（2，0），若抛物线 y= x2+k 与扇形 OAB 的边界总有两个公共点，则实数 k 的取值范围是 ． 考点：二次函数的性质．[来源~:#^@ 中国%教育出版网] 分析：根据∠AOB=45°求出直线 OA 的解析式，然后与抛物线解析式联立求出有一个公共点时的 k 值， 即为一个交点时的最大值，再求出抛物线经过点 B 时的 k 的值，即为一个交点时的最小值，然后写出 k 的取值范围即可．[来@源:中国教育*出#%版网&] 解答：解：由图可知，∠AOB=45°， ∴直线 OA 的解析式为 y=x， 联立 消掉 y 得， x2﹣2x+2k=0，[中国教育出版@^&网*%] △=（﹣2）2﹣4×1×2k=0， 即 k= 时，抛物线与 OA 有一个交点， 此交点的横坐标为 1， ∵点 B 的坐标为（2，0）， ∴OA=2， ∴点 A 的坐标为（ ， ），[中国%#教&育出^版网*][中国#教~^@育% 出版网] ∴交点在线段 AO 上； 当抛物线经过点 B（2，0）时， ×4+k=0， 解得 k=﹣2，[ww*w.z#zs~tep.co^m@] ∴要使抛物线 y= x2+k 与扇形 OAB 的边界总有两个公共点，实数 k 的取值范围是﹣2＜k＜ ．[来源:zzs^tep%.~com@&] 故答案为：﹣2＜k＜ ． 点评：本题考查了二次函数的性质，主要利用了联立两函数解析式确定交点个数的方法，根据图形求 出有一个交点时的最大值与最小值是解题的关键． [来%源:中教~#& 网^] 5. 2013•衢州 4 分）某果园有 100 棵橘子树，平均每一棵树结 600 个橘子．根据经验估计，每多种一颗树， 平均每棵树就会少结 5 个橘子．设果园增种 x 棵橘子树，果园橘子总个数为 y 个，则果园里增种 棵橘 子树，橘子总个数最多． 【思路分析】根据题意设多种 x 棵树，就可求出每棵树的产量，然后求出总产量 y 与 x 之间的关系式，进 而求出 x=﹣ 时，y 最大 【解析】假设果园增种 x 棵橙子树，那么果园共有（x+100）棵橙子树，[来@源:^中国教~育%出版#网] ∵每多种一棵树，平均每棵树就会少结 5 个橙子， ∴这时平均每棵树就会少结 5x 个橙子， 则平均每棵树结（600﹣5x）个橙子． ∵果园橙子的总产量为 y， ∴则 y=（x+100）（600﹣5x） =﹣5x2+100x+60000， ∴当 x=﹣ =﹣ =10（棵）时，橘子总个数最多 【方法指导】此题主要考查了二次函数的应用，准确分析题意，列出 y 与 x 之间的二次函数关系式是解题 关键 6.（2013 山西，18，3 分）如图是我省某地一座抛物线形拱桥，桥拱在竖直平面内，与水平桥面相交于 A， B 两点，桥拱最高点 C 到 AB 的距离为 9m，AB=36m，D，E 为桥拱底部的两点，且 DE∥AB，点 E 到直线 AB 的距离为 7m，则 DE 的长为_____m. 【答案】48 【解析】以 C 为原点建立平面直角坐标系，如右上图，依题意，得 B（18，－9）， 设抛物线方程为： 2y ax ，将 B 点坐标代入，得 a＝－ 1 36 ，所以，抛物线方程为： 21 36y x  ， E 点纵坐标为 y＝－16，代入抛物线方程，－16＝ 21 36 x ，解得：x＝24，所以，DE 的长为 48m。 7.（2013 四川绵阳，18，4 分）二次函数 y=ax2+bx+c 的图象如图所示，给出下列结论：①2a+b＞0；②b＞a ＞c；③若-1＜m＜n＜1，则 m+n＜ ；④3|a|+|c|＜2|b|。其中正确的结论是 ① ③ ④ （写出你认 为正确的所有结论序号）. ［解析］抛物线开口向下，a <0, 2a<0,对称轴 x= -b 2a >1,-b<2a ,2a+b>0 ，①正确； -b<2a ,b>-2a>0>a , 令抛物线的解析式为 y=- 1 2 x2 +bx- 1 2 ,此时，a=c,欲使抛物线与 x 轴交点的横坐标分别为 1 2 和 2， 则（1 2 +2）/2=-b/(- 1 2 ),b= 5 4 , 抛物线 y=- 1 2 x2 + 5 4 x- 1 2 符合“开口向下，与 x 轴的一个交点的横坐 标在 0 与 1 之间，对称轴在直线 x=1 右侧”的特点，而此时 a=c（其实 a>c,a1，-b a >2，m+n<-b a ，③正确； 当 x=1 时， a+b+c>0,2a+b>0,3a+2b+c>0, 3a+c>-2b, -3a-c<2b , a<0 , c<0 , b>0 , 3|a|+|c|=-3a-c<2b=2|b|,④正确。 [来%&~源 三、解答题 1．（2013 重庆市(A)，25，12 分）如图，对称轴为直线 x＝－1 的抛物线 y＝ax2＋bx＋c(a≠0)与 x 轴相交于 A、B 两点，其中点 A 的坐标为（－3，0）． （1）求点 B 的坐标； （2）已知 a=1，C 为抛物线与 y 轴的交点． ①若点 P 在抛物线上，且 S△POC＝4S△BOC，求点 P 的坐标； ②设点 Q 是线段 AC 上的动点，作 QD⊥x 轴交抛物线于点 D，求线段 QD 长度的最大值． [中国#@*教~育出&版网] 【答案】（1）∵点 A（－3，0）与点 B 关于直线 x＝－1 对称， ∴点 B 的坐标为（1，0）． （2）∵a＝1，∴y＝x2＋bx＋c． ∵抛物线过点（－3，0），且对称轴为直线 x＝－1， ∴b＝2，c＝－3，∴y＝x2＋2x－3，且点 C 的坐标（－3，0）．[中^国教*~育&% 出版网] 1 设点 P 的坐标为（x，y），由题意得 S△BOC＝ 1 2 ×1×3＝ 3 2 ，∴S△POC＝6．[来源#~:%zzs@te^p.com] 当 x＞0 时，有 1 2 ×3×x＝6，∴x＝4，∴y＝42＋2×4－3＝21．[www^.#z&zstep*.c@om] 当 x＜0 时，有 1 2 ×3×(－x)＝6，∴x＝－4，∴y＝(－4)2＋2×(－4)－3＝5． ∴点 P 的坐标为（4，21）或（－4，5）． ②∵直线 y＝x＋b 过 A、C 两点， ∴ .3.3 ,1 .3 ,03            xyn m n nm 解得 设点 Q 的坐标为（x，y），－3≤x≤0， 则有 QD＝－x－3－(x2＋2x－3)＝－x2－3x=－ 23 9( )2 4x   ． ∵－3≤－ 3 2 ≤0， ∴当 x＝－ 3 2 时，QD 有最大值 9 4 ．[来%源:^中国教育&出版*网#] ∴线段 QD 长度的最大值为 9 4 ． [来源:~@%*中国教育出版网#] 【解析】（1）由抛物线的轴对称性容易求解．（2）①先求出△BOC 的面积，然后以 OC 为底边，点 P 到 OC 的距离，即点 P 的横坐标的绝对值为高，表示△POC 的面积，进而求出点 P 的横坐标，再将其代入抛物线 的解析式求得点 P 的纵坐标解决问题．②构建线段 OD 长关于点 Q 的横坐标的二次函数模型，利用二次函 数的性质求解． 【方法指导】本题考查轴对称，求二次函数的解析式，平面直角坐标系中的图形面积，二次函数的最值．第 （2）问中①在表示△POC 的面积时，启示我们在坐标系中求三角形的面积时，一般是将坐标轴上的边作 为底边，而将该边所对的顶点的横（纵）坐标的绝对值作为高．通过第（3）问可总结出表示平行于 y 轴 的直线上两点的距离时，需用上面点的纵坐标减下面点的纵坐标来求，简称“上纵－下纵”．同理，表示 平行于 x 轴的直线上两点的距离时，需用右边点的横坐标减左边点的横坐标来求，简称“右横－左横”． 2.（2013 湖北黄冈，23，12 分）某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外 市场上全部售完，该公司的年产量为 6 千件，若在国内市场销售，平均每件产品的利润 y1（元）与国内销 售数量 x（千件）的关系为：[来源:Zxxk.Com]    1 15 90 0 2 5 130 2 6 x x y x x     ＜ ≤ ≤ ＜ 若在国外销售，平均每件产品的利润 y2（元）与国外的销售数量 t（千件）的关系为：[ww#w.zzs^tep.~*com%]    2 100 0 2 5 110 2 6 t y t t    ＜ ≤ ≤ ＜ [www.z%#z&ste*@p.com] （1） 用 x 的代数式表示 t 为：t＝ ；当 0＜x≤4 时，y2 与 x 的函数关系为 y2＝ ；当≤x＜ 时，y2＝100；[w~ww.zz&step%.#com@] （2）求每年该公司销售这种健身产品的总利润 w（千元）与国内的销售数量 x（千件）的函数关系式，并 指出 x 的取值范围； （3）该公司每年国内、国外的销售量各为多少时，可使公司每年的总利润最大？最大值为多少？ 【答案】解：（1）t＝6－x；当 0＜x≤4 时，y2＝－5(6－x)＋110＝5x＋80． 当 4≤x＜6 时，y2＝100． （2）当 0＜x≤2 时，w＝(15x＋90)x＋(5x＋80)(6－x)＝10x2＋40x＋480； 当 2＜x≤4 时，w＝(－5x＋130)x＋(5x＋80)(6－x)＝－10x2＋80x＋480； 当 4＜x＜6 时，w＝(－5x＋130)x＋100(6－x)＝－5x2＋30x＋600； 2 2 2 10 40 480(0 2) 10 80 480(2 4) 5 30 600(4 6) x x x w x x x x x x           ＜ ≤ ＜ ≤ ＜ ＜ （3）当 0＜x≤2 时，w＝10x2＋40x＋480＝10(x＋2)2＋440．此时 x＝2 时，w 最大＝600． 当 2＜x≤4 时，w＝－10x2＋80x＋480＝－10(x－4)2＋640．x＝4 时，w 最大＝640．[中国教育@出~^版*网&] 当 4＜x＜6 时，w＝－5x2＋30x＋600＝－5(x－3)2＋645．4＜x＜6 时，w＜640． ∴x＝4 时，w 最大＝640． 国内 4 千件，国外 2 千件，最大利润为 64 万元（或 640 千元）． 【解析】（1）根据“每年可在国内、国外市场上全部售完，该公司的年产量为 6 千件”，知 x＋t＝6，据此 易解第（1）问． （2）w 等于国内销售总利润与国外销售总利润的和，即 w＝y1x＋y2(6－x)．根据第（1）问可得    2 5 80 0 4 100 4 6 x x y t     ＜ ≤ ≤ ＜ ，结合    1 15 90 0 2 5 130 2 6 x x y x x     ＜ ≤ ≤ ＜ ，可知 w 与 x 之间属于分段函数关系，自变量 x 的 取值范围分别是 0＜x≤2，2＜x≤4，4＜x≤6．然后将不同取值范围下的解析式代入 w＝y1x＋y2(6－x)中得 解． （3）对（2）中 w 与 x 之间的各段二次函数关系配方，得出各最大值情况，再把它们进行对比，获得最后 的最大值． 【方法指导】本题考查构建二次函数模型求最大值，涉及列函数解析式，配方，二次函数的增减性、极值．这 类分段函数问题涉及数量众多，关系错综复杂，求解关键是抓住主要相等关系（如本例中“总利润 w＝国 内销售总利润＋国外销售总利润＝y1x＋y2(6－x)”），然后理清各段情况下自变量的取值范围并求出相应函 数关系式，这是关键中的关键，最后将它们整体代入主要相等关系式中分类讨论获解．[来~*源:中国教育&出^版@网] 3．（2013 江苏苏州，29，10 分）如图，已知抛物线 y＝ 1 2 x2＋bx＋c（b，c 是常数，且 c<0）与 x 轴分别交 于点 A，B（点 A 位于点 B 的左侧），与 y 轴的负半轴交于点 C，点 A 的坐标为(－1，0)． (1)b＝ ▲ ，点 B 的横坐标为 ▲ （上述结果均用含 c 的代数式表示）； (2)连接 BC，过点 A 作直线 AE∥BC，与抛物线 y＝ 1 2 x2＋bx＋c 交于点 E．点 D 是 x 轴上一点，其坐标 为(2，0)，当 C，D，E 三点在同一直线上时，求抛物线的解析式； (3)在(2)的条件下，点 P 是 x 轴下方的抛物线上的一动点，连接 PB，PC，设所得△PBC 的面积为 S． ①求 S 的取值范围； ②若△PBC 的面积 S 为整数，则这样的△PBC 共有 ▲ 个． 【思路分析】（1）由 A(－1，0)在抛物线 y＝ 1 2 x2＋bx＋c 上可以解决． （2）先求直线 AE 的解析式，再求直线 CD 的解析式，最后求抛物线的解析式． （3）先求直线 CB 的解析式，再分类讨论点 P 的不同位置 S 的取值范围． 【解】（1） 1 2 ＋c，－2c；[来%源^:zzst~ep.com@&] 【方法指导】①抛物线与 x 轴的交点的横坐标是令 y 为 0 的一元二次方程的两根；②结合点的坐标特征将 几何线段的长用坐标表示是勾通代数与几何的关键；③用解析式联立方程组可以求两个图象的交点；④本 题第 3 问，是动点探索型问题，要能灵活运用所学的知识，注意思想方法的运用． 【易错警示】不注意点的坐标的符号特征，错误表达几何线段的长；推导不仔细出错．没有考虑分类讨论．[来 源#~@:*zzstep&.com] 4. （2013 江苏扬州，26，10 分）如图，抛物线 822  xxy 交 y 轴于点 A，交 x 轴正半轴于点 B. （1）求直线 AB 对应的函数关系式； （2）有一宽度为 1 的直尺平行于 y 轴；在点 A、B 之间平行移动；直尺两边长所在直线被直线 AB 和抛物 线截得两线段 MN、PQ.设 M 点的横坐标为 m ；且 30  m .试比较线段 MN 与 PQ 的大小. 【思路分析】（1）只要求出抛物线与 x 轴、y 轴的交点 A、B 的坐标即可求出直线 AB 对应的函数关系式； （2）用含 m 的代数式表示出 M、N、P、Q 的坐标，分别求出 MN、PQ 的长即可解决问题． 【解】（1）令 822  xxy =0，得 1 2x   ， 2 4x  .令 x=0,得 y=－8. ∴  0, 8A  ，  4,0B .设直线 AB 对应的函数关系式为 y kx b  ，则 8, 4 0. b k b      解得 2k  ， 8b   .∴直线 AB 对应的函数关系式为 82  xy ； （2）因为直尺的宽度为 1，M、N 横坐标均为 m ，∴P、Q 的横坐标均为 m +1， 据题意得，M、N 纵坐标分别为 2 m －8、 2 2 8m m  ，可得 MN= mm 42  ； 同理可得 PQ= 322  mm .[w^ww.zz&step.com#~*] ∴    2 24 2 3 2 3MN PQ m m m m m          ，∵ 30  m ∴当 5.10  m 时， 2 3 0m   ， PQMN  ； 当 m =1.5 时， 2 3 0m   ，MN=PQ； 当 35.1  m 时， 2 3 0m   PQMN  . 【方法指导】已知点在图象上，则点的坐标适应解析式．[来%源:@~z&zstep#.com] 【易错警示】对于（2）没有分类讨论，漏掉其中一种或两种情况． 5.（2013 贵州安顺，26，14 分） 如图，已知抛物线于 x 轴交于 A（－1,0）、B（3,0）两点，与 y 轴交于点 C（0,3）。 （1）求抛物线的解析式； （2）设抛物线的顶点为 D，在其对称轴的右侧的抛物线上是否存在点 P，使得△PDC 是等腰三角形，若存 在，求出符合条件的点 P 的坐标；若不存在，请说明理由：[来@源:~中&#教网^] （3）若点 M 是抛物线上一点，以 B、C、D、M 为顶点的四边形是直角梯形，试求出点 M 的坐标。 【思路分析】（1）由于 A（﹣1，0）、B（3，0）、C（0，3）三点均在坐标轴上，故设一般式解答和设交点 式（两点式）解答均可． （2）分以 CD 为底和以 CD 为腰两种情况讨论．运用两点间距离公式建立起 P 点横坐标和纵坐标之间的关 系，再结合抛物线解析式即可求解． （3）根据抛物线上点的坐标特点，利用勾股定理求出相关边长，再利用勾股定理的逆定理判断出直角梯 形中的直角，便可解答．[中~国%&*教育出^版网] 【解】（1）∵抛物线与 y 轴交于点 C（0，3），∴设抛物线解析式为 y=ax2+bx+3（a≠0）， 根据题意，得 ，解得 ， ∴抛物线的解析式为 y=﹣x2+2x+3． （2）存在。 由 y=－x2+2x+3，得 D 点坐标为（1,4），对称轴为 x=1。 ①若以 CD 为底边，则 PD=PC，设 P 点坐标为（x，y）,根据勾股定理，得 x2+(3－y)2=（x－1）2+(4－y)2, 即 y=4－x。又点 P（x，y）在抛物线上，∴4－x=－x2+2x+3，即 x2－3x+1=0。解得 x= 2 53  。 ∵ 2 53  ＜1，应舍去，∴x= 2 53  。y=4－x= 2 55  。即点 P 的坐标为（ 2 53  ， 2 55  ）。 ②若以 CD 为一腰，因为点 P 在对称轴右侧的抛物线上，由抛物线对称性知，点 P 与点 C 关于直线 x=1 对 称，此时 P 点坐标为（2，3）。 ∴符合条件的点 P 的坐标为（ 2 53  ， 2 55  ）或（2，3）。 （3）由 B(3,0)，C（0,3）,D（1,4），根据勾股定理，得 CB= 23 ，CD= 2 ，BD= 52 。 ∴CB2+CD2=BD2=20. ∴∠BCD=90°， 设对称轴交 x 轴于点 E，过 C 做 CM⊥DE，交抛物线于点 M，垂足为 F。[来源:*#z~zste@p.^com] 在 Rt△DCF 中，∵CF=DF=1，∴∠CDF=45°， 由抛物线的对称性知，∠CDM=2×45°=90°，点 M 坐标为（2,3） ∴DM∥BC。∴四边形 BCDM 为直角梯形。 由∠BCD=90°及题意可知， 以 BC 为一底时，顶点 M 在抛物线上的直角梯形只有上述一种情况： 以 CD 为一底或以 BD 为一底，且顶点 M 在抛物线上的直角梯形均不存在。[中国教育出版@^&网*%] 综上所述，符合条件的点 M 的坐标为（2，3）． 【方法指导】此题是一道 “存在性问题”，结合二次函数图象和等腰三角形、等腰梯形的性质，考查了它们 存在的条件，有一定的开放性． 6．（2013 山东临沂，26，13 分）如图，抛物线经过 A（－1，0），B（5，0），C（0，－ 5 2 ）三点． （1）求抛物线的解析式； （2）在抛物线的对称轴上有一点 P，使 PA＋PC 的值最小，求点 P 的坐标； （3）点 M 为 x 轴上一动点，在抛物线上是否存在一点 N，使以 A，C，M，N 四点构成的四边形为平行四边 形？若存在，求点 N 的坐标；若不存在，请说明理由． y xOA B C 【答案】：解：（1）设抛物线的解析式为 y＝ax2＋bx＋c，根据题意，得 0 25 5 0 5 2 a b c a b c c              ， ， ． 解得 1 2 2 5 2 a b c           ， ， ． ∴ 抛物线的解析式为： 21 522 2y x x   ． （2）由题意知，点 A 关于抛物线对称轴的对称点为点 B，连接 BC 交抛物线的对称轴于点 P，则 P 点即为 所求．设直线 BC 的解析式为 y＝kx＋b， 由题意，得 5 0 5 2 k b b     ， ， 解得 1 2 5 2 k b      ， ， ∴直线 BC 的解析式为 1 5 2 2y x  ． ∵抛物线 21 522 2y x x   的对称轴是 x＝2，[来%源:@中^国教~育出版#网] ∴当 x＝2 时， 1 5 3 2 2 2y x    ． ∴点 P 的坐标是（2， 3 2  ）． （3）存在． （ⅰ）当存在的点 N 在 x 轴的下方时，如图所示， ∵四边形 ACNM 是平行四边形，∴CN∥x 轴， ∴点 C 与点 N 关于对称轴 x＝2 对称． ∵C 点的坐标为（0， 5 2  ）， ∴点 N 的坐标为（4， 5 2  ）． （ⅱ）当存在的点 N′在 x 轴上方时，如图所示，作 N′H⊥x 轴于点 H， ∵四边形 ACM′N′是平行四边形， ∴AC＝M′N′，∠N′M′H＝∠CAO， ∴Rt△CAO≌Rt△N′M′H，∴N′H＝OC．[来&源:中^国%教育出*版网#] ∵点 C 的坐标为（0， 5 2  ），∴N′H＝ 5 2 ，即 N′点的纵坐标为 5 2 ， ∴ 21 5 522 2 2x x   ，解得 x1＝ 2 14 ，x2＝ 2 14 ．[来源%:#中国~教*育@出版网] ∴点 N′的坐标为（ 2 14 ， 5 2 ）和（ 2 14 ， 5 2 ）． 综上所述，满足题目条件的点 N 共有三个，分别为（4， 5 2  ），（ 2 14 ， 5 2 ），（ 2 14 ， 5 2 ）． y xOA B C P N M N′ M′ H 【方法指导】利用待定系数法求出解析式；本题考查了对称、特殊的四边形、二次函数的图象多个知 识点。[中^#国教%育出&@版网] 7．（2013 山东滨州，23，9 分）某高中学校为高一新生设计的学生单人桌的抽屉部分是长体方形，抽屉底 面周长为 180cm，高为 20cm．请通过计算说明，当底面的宽 x 为何值时，抽屉的体积 y 最大？最大为多少？ (材质及其厚度等暂忽略不计) 【答案】：解：根据题意，得 y = 20·x·(180 2 －x)， 整 理， 得 y =－20x2 + 1800x． ∵ y =－20x2 + 1800x =－20(x2－90x+2025) + 40500 =－20(x－45)2 + 40500， ∵a=－20＜0，∴当 x = 45时，函数 y 有最大值，y 最大值= 40500，[来&源:中教^@*#网] 答：当底面的宽为 45cm 时，抽屉的体积最大，最大为 40500cm3． 【解析】根据题意列出二次函数关系式，然后利用二次函数的性质求最大值．[来源:zz@st%ep~.c*&om] 【方法指导】本题考查利用二次函数解决实际问题．求二次函数的最大（小）值有三种方法，第一种可由 图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数 a 的绝对值是较小 的整数时，用配方法较好，如 y=－x2－2x+5，y=3x2－6x+1 等用配方法求解比较简单． 8. （2013 四川宜宾，23，10 分）[来源:中*国教育出^版网%~#] 某商品的进价为每件 40 元，售价为每件 50 元，每个月可卖出 210 件；如果每件商品的售价每上涨 1 元．则 每个月少卖 10 件(每件售价不能高于 65 元)．设每件商品的售价上涨 x 元(x 为正整数)，每个月的销售利润 为 y 元． (1)求 y 与 x 的函数关系式并直接写出自变量 x 的取值范围； (2)每件商品的售价定为多少元时，每个月可获得最大利润?最大的月利润是多少元? (3)每件商品的售价定为多少元时，每个月的利润恰为 2200 元?根据以上结论，请你直接写出售价在什么范 围时，每个月的利润不低于 2200 元?[来源%:中~教网#@^] 【思路分析】（1）每月的销售利润=每件的利润×每月卖的件数；由进价为每件 40 元，每件售价不能高于 65 元可求出自变量 x 的取值范围. （2）把问号（1）的结论配方即可求出答案. （3）令 y=2200 可求出第一个问号，第二个问号可根据图象得出. 【解】 (1) );150(210011010)4050)(10210( 2 为正整数且xxxxxxy  [来@#源^:%*中教网] (2) .5.2402)5.5(10 2  xy ∵a=－10<0，∴当 x=5.5 时，y 有最大值 2402.5． ∵ 150  x ，且 x 为整数， 当 x=5 时，50+x=55，y=2400(元)，当 x=6 时，50+x=56，y=2400(元) ∴当售价定为每件 55 或 56 元，每个月的利润最大，最大的月利润是 2400 元． (3)当 .10,1:,2200210011010,-2200 21 2  xxxxy 解得时 当 x=1 时，50+x=51，当 x=10 时，50+x=60． ∴当售价定为每件 51 或 60 元，每个月的利润为 2200 元． 当售价不低于 51 或 60 元，每个月的利润为 2200 元． 当售价不低于 51 元且不高于 60 元且为整数，每个月的利润不低于为 2200 元．(或当售价分别为 51，52，53，54，55，56，57，58，59，60 元时， 每个月的利润不低于为 2200 元) 【方法指导】要求哪个量的最大值应先把这个量用函数解析式表达出来，常用的数量关系为总利润=每件 的利润×卖出的总件数.类似于问号（3）中的第二个问题要画出函数图象，结合函数图象解决.[来@源#:中国教育出版*网&~] 9. （2013 四川宜宾，25，12 分） 如图，抛物线 abxaxy 42  经过 A(－1，0)、C(0，4)两点，与 x 轴交于另一点 B． (1)求抛物线的解析式； (2)已知点 D(m，m＋１)在第一象限的抛物线上，求点 D 关于直线 BC 对称的点的坐标； (3)在(2)的条件下，连接 BD，点 P 为抛物线上一点，且∠DBP=45°，求点 P 的坐标． 【思路分析】（1）把点 A(－1，0)、C(0，4)的坐标带入 abxaxy 42  可求出 a，b 从而求出抛物线的 解析式. （2）把点 D(m，m＋１)代入抛物线的解析式可求出点 D 的坐标为(3，4)，因为 C 的坐标为（0,3）所以 CD∥AB， 且 CD=3，根据轴对称的性质可知 CE=CD=3，所以 OE=1，∴E(0，1)． （3）可把点 P 的坐标用字母表示出来，再把点 P 代入抛物线解析式中求出字母的值即可求出点 P 的坐标. 由（1），（2）知 OC=OB=4，所以∠OBC=∠OCB=45°,因为 CD∥AB 所以∠OBC=∠OCB∠DCB=45°过点 D，P 分别 作 x 轴 的 垂 线 垂 足 分 别 为 E, F 可 求 出 DE=CE= 2 23 ， BE=BC － CE= ,2 25 所 以 .5 3tantan  BE DECBDPBF 设 PF=3t，则 BF=5t，∴OF=5t－4 可表示出 P 点的坐标，代入解析式 即可求出点 P 的坐标. 【解】 (1) ∵抛物线 abxaxy 42  经过 A(－1，0)、C(0，4)两点      .44 ,04 a aba      .3 1 b a解得 ∴抛物线的解析式为 .432  xxy (2)∵点 D (m，m＋１)在抛物线上，∴ ,431 2  mmm 即 ,0322  mm ∴ .31  mm 或 ∵点 D 在第一象限，∴点 D 的坐标为(3，4)．[www#.zz*^ste&p.co@m] 由(1)知 OA=OB，∴∠CBA=45°．[www^.%zzste&p.~c#om] 设点 D 关于直线 BC 的对称点为点 E．[来源*:#% 中&教~网] ∵C(0，4)，∴CD∥AB，且 CD=3， ∴∠ECB=∠DCB=45°， ∴E 点在 y 轴上，且 CE=CD=3． ∴OE=1，∴E(0，1)． 即点 D 关于直线 BC 的对称的点的坐标为(0，1)． (3)作 PF⊥AB 于 F，DE⊥BC 于 E． 由(1)有： OB=OC=4，∴∠OBC=45°， ∵∠DBP=45°， ∴∠CBD=∠PBA．[来#&~源:@中^教网] ∵C(0，4)，D(3，4)，∴CD∥OB 且 CD=3． ∴∠DCE=∠CBO=45°， ∴DE=CE= 2 23 ． ∵OB=OC=4，∴BC= 24 ，∴BE=BC－CE= ,2 25 ∴ .5 3tantan  BE DECBDPBF 设 PF=3t，则 BF=5t，∴OF=5t－4， ∴P(－5t+4，3t)． ∵P 点在抛物线上， ∴ ,4)45(3)45(3 2  ttt ∴ ,25 22)(0  tt 或舍去 ∴ ).25 66,5 2(P [来源@:zzs*te#%^p.com] 【方法指导】求抛物线的解析式应先根据题意假设适当地解析式形式常用的有（1）顶点式：y=a(x－h)2+k； [来~源^*:&中教%网] (2)交点式：y=a(x－x1)(x－x2)；（3）一般式：y=ax2+bx+c (4)若抛物线经过原点可假设解析式为：y=ax2+bx. 求对称点的坐标要根据轴对称或中心对称的的性质去求，应熟练掌握两种对称的性质.注意点的横纵坐标 可以与线段的长度互相转化但要注意坐标的符号.解直角坐标系的综合题时常用的辅助线为作 x 轴或 y 轴 的垂线. 已知点的横坐标或纵坐标要求点的坐标时可直接把点的坐标带入解析式，若横纵坐标均不知道可 把点的横纵坐标用字母表示出来，再把点的横纵坐标代入抛物线解析式中先求出字母的值而后可求出点的 坐标. 10.（2013 四川泸州，25，12 分）如图，在直角坐标系中，点 A 的坐标为 2（ ，0），点 B 的坐标为 1 3（， ）， 已知抛物线 2 ( 0)y ax bx c a    经过三点 A、B、O(O 为原点)． （1）求抛物线的解析式； （2）在该抛物线的对称轴上，是否存在点 C，使 BOC 的周长最小．若存在，求出点 C 的坐标．若不存 在，请说明理由； （3）如果点 P 是该抛物线上 x 轴上方的一个动点，那么 PAB 是否有最大面积．若有，求出此时 P 点的 坐标及 PAB 的最大面积；若没有，请说明理由．（注意：本题中的结果均保留根号）． 【答案】（1）∵抛物线 2y ax bx c   （ 0a  ）过点 A、B、O， 且 0c  ， 解得： 3 3 2 3 3 0 a b c            ∴所求抛物线的解析式为 23 2 3 3 3y x x   ； （2）存在，由 23 2 3 3 3y x x   ，配方后得：  23 313 3y x    ， 抛物线的对称轴 1x   ，[来源:zzstep%.c@#o*&m] ∵点 C 在对称轴上， △BOC 的周长＝OB＋BC＋CO，而 OB＝  221 3 2  ， 要使△BOC 的周长周长最小，必须 BC＋CO 最小， ∵点 O 与点 A 关于直线 1x   对称，有 CO＝CA，[来@源:%*中教^网~] △BOC 的周长＝OB＋BC＋CO＝ OB＋BC＋CA． 当 A、B、C 三点共线时，即点 C 是直线 AB 与对称轴的交点时，BC＋CA 最小， 此时△BOC 的周长最小，设直线 AB 的解析式为： y kx b  ，则有 3 2 0 k b k b       ， 解得 3 3k   ， 2 3 3b   ． ∴直线 AB 的解析式为 3 2 3 3 3y x   ， 当 1x   时， 3 3y   ， ∴C 的坐标为（－1， 3 3  ）； （3）设 P ,x y （ 2 0, 0x y    ），[来&源:*zzstep.c@~om%] 则 23 2 3 3 3y x x   ……………… ① 过点 P 作 PQ⊥ y 轴于点 Q，PG⊥ x 轴于点 G，过点 A 作 AF⊥PQ 于点 F，过点 B 作 BE⊥PQ 于点 E，则 PQ ＝ x ，PG＝ y ， 由题意得： PAB AFP BEPAFEBS S S S   梯形 ＝   1 1 11 22 2 2AF BE AF FP PE BE     3 3 32 2y x   23 1 9 3 2 2 8x       ……………… ② 把①代入②得： 23 3 2 3 3 32 3 3 2PABS x x x          ＝ 23 3 32 2x x   23 1 9 3 2 2 8x       ． 当 1 2x   时，△PAB 的面积最大，最大值是 9 3 8 ，[w~%ww#.z*zstep.com^] 此时 3 1 2 3 1 3 3 4 3 2 4y        ， ∴P 的坐标为（ 1 2  ， 3 4  ）． 【解析】（1）直接将 A、O、B 三点坐标代入抛物线解析式的一般式，可求解析式；[来~源^:中国%教育&*出版网] （2）因为点 A，O 关于对称轴对称，连接 AB 交对称轴于 C 点，C 点即为所求，求直线 AB 的解析式，再根 据 C 点的横坐标值，求纵坐标； （3）设 P（x，y）（－2＜x＜0，y＜0），用割补法可表示△PAB 的面积，根据面积表达式再求取最大值时， x 的值． 【方法指导】考查了坐标系中点的坐标求法，抛物线解析式的求法，根据对称性求线段和最小的问题，也 考查了在坐标系里表示面积及求面积最大值等问题；解答本题（3）也可以将直线 AB 向下平移至与抛物线 相切的位置，联立此时的直线解析式与抛物线解析式，可求唯一交点 P 的坐标． 13. 2013 广东省，23，9 分）已知二次函数 12 22  mmxxy ． （1）当二次函数的图象经过坐标原点 O（0，0）时，求二次函数的解析式； （2）如题 23 图，当 m=2 时，该抛物线与 y 轴交于点 C，顶点为 D，求 C、D 两点的坐标； （3）在（2）的条件下，x 轴上是否存在一点 P，使得 PC+PD 最短？若 P 点存在，求出 P 点的坐标；若 P 点不存在，请说明理由． [来#源:zzs*tep.~com@^] 【思路分析】对于(1)，把原点坐标代入解析式即可求得 m 的值． 对于(2)，把 m=2 代入解析式，然后利用顶点坐标公式以及求交点坐标的方法即可求得 C、D 坐标． 对于(3)，利用△COP∽△CED 和前两问求出的三角形的边长即可求得 OP 的长，进而求得答案． 【解】（1）把原点 O 的坐标（0，0）代入 12 22  mmxxy 得 012 m ，解得 m=±1.[来源:学§科§网] 所以，二次函数解析式为 xxy 22  或 xxy 22  （2）把 m=2 代入 12 22  mmxxy ，得 342  xxy ， 令 x=0，得 y=3，所以 C 点坐标为（0，3），[www.z*%^z~step.co#m] 342  xxy 配方，得 1)2( 2  xy ，所以 D 点坐标为（2，－1）. （3）如图，连结 CD，并作 DE⊥y 轴于 E， [来源:#*中教^~网%] ∵C 点坐标为（0，3），D 点坐标为（2，－1） ∴CE=4，DE=2， ∵DE⊥y， ∴OP∥DE ∴△COP∽△CED ∴ DE OP CE CO  ，即 24 3 OP ∴OP=1.5， ∴P 点的坐标为（1.5，0）. 【方法指导】 (1)已知函数的图象经过某已知点，通常都是把这个点的坐标代入解析式，从而求得待定系 数，最终求得解析式；(2)求抛物线的顶点坐标通常只需要用顶点坐标公式即可求出，求与坐标轴的交点坐 标，往往是将 x 轴和 y 轴分别看作 y=0 和 x=0，代入函数式求公共解，即交点坐标；(3)在第（1）和（2） 的基础上，可以求出相似三角形的边长，然后利用相似三角形的性质可以求出边长． 14．（2013 浙江台州，23，12 分）如图 1，已知直线 l： 2 xy 与 y 轴交于点 A，抛物线 kxy  2)1( 经过点 A，其顶点为 B，另一抛物线 hhxy  2)( 2 （h>1）的顶点为 D，两抛物线相交于点 C， （1）求点 B 的坐标，并说明点 D 在直线 l 上的理由； （2）设交点 C 的横坐标为 m． ①交点 C 的纵坐标可以表示为： 或 ，由此请进一步探究 m 关于 h 的函数关系式； ②如图 2，若∠ACD=90°，求 m 的值． M NE C D A B D0 x y A B C 0 x y 第 23 题 【思路分析】（1）由 2 xy 与 y 轴交于点 A，易得 A（0,2），又由抛物线 kxy  2)1( 经过点 A（0,2）， 可以将 A 点横、纵坐标代入二次函数解析式，可求出 k 的值，从而确定顶点 B 的坐标；由于 D 点是 hhxy  2)( 2 的顶点，易得 D（h，2－h），如要判断点 D 在直线 l 上，需要将 D 点的坐标，代入直 线解析式中验证。 （2）○1 由于点 C 是两抛物线的交点，可将 C 点的横坐标 m 分别代入两个抛物线解析式，从而求出两种不 同表示的 C 点纵坐标；欲探究 m 关于 h 的函数关系式，需找到 m 和 h 的等量关系，由于两种不同表示方 法表示的都是 C 点纵坐标，二者相等列等式，再变形为函数关系式。○2 有∠ACD=90°这一特殊条件，再 作 x 轴、y 轴的垂线，从而构造相似三角形，利用相似三角形的对应边的比相等，列出关于 m 的方程，从 而求出 m 的值。 【解】（1）由题意可知 A（0，2），又因为抛物线 kxy  2)1( 经过点 A，所以有 k 2)10(2 ，解 得 1k ，所以抛物线解析式为 1)1( 2  xy ，从而得出点 B 的坐标为（1，1）；因为点 D 是抛物线 hhxy  2)( 2 （h>1）的顶点，所以点 D 的坐标为（h，2－h），将（h，2－h）代入 2 xy 中， 左右两边相等，所以点 D 在直线 l 上． （2）①交点 C 的纵坐标可以表示为： 1)1( 2 m 或 hhm  2)( 2 由题意知： 1)1( 2 m = hhm  2)( 2 ， 整理得： 02)21(2  mhmh ， 解得， mh 2 或 1h ，[中国#教育出@版~^网*] ∵h>1 ∴ 2 hm  ． ②过点 C 作 CM⊥y 轴，垂足为点 M，过点 D 作 DE⊥y 轴，垂足为点 E，过点 C 作 CN⊥DE，垂 足为点 N，则四边形 CMEN 是矩形， ∴∠MCN=90°， 又∵∠ACD=90° ∴∠MCA=∠DCN[来#源:%*^中教网&] ∴△ACM∽△DCN ∴ DN AM CN CM  由题意可知 CM=m，AM= mm 22  ，CN= hmm  22 ，DN= mh  从而有 mh mm hmm m    2 2 2 2 ， 由①得 mh 2 ， ∴ 0122  mm 解得， 21m ， 又∵点 C 在第一象限内， ∴ 21m 【方法指导】本题考查待定系数法求二次函数解析式、二次函数的顶点坐标、相似三角形的判定和性质、 一元二次方程的解法等知识点，本题对学生的综合解题能力要求偏高。对于二次函数，我们需要了解顶点 式和一般式两种常见形式，能够熟练的说出它的开口方向、顶点、对称轴等常用知识点。[ww~w.zzs@t#%ep.&com] 2．(2013 浙江湖州,19,8 分)已知抛物线 2y x bx c    经过点 A（3，0），B（－1，0）． （1）求抛物线的解析式； （2）求抛物线的顶点坐标． 【思路分析】（1）根据抛物线 y=－x2+bx+c 经过点 A（3，0），B（－1，0），直接得出抛物线的解析式为； y=－（x－3）（x+1），再整理即可， （2）根据抛物线的解析式为 y=－x2+2x+3=－（x－1）2+4，即可得出答案． 【解】（1）解法一：∵抛物线 2y x bx c    经过点 A（3，0），B（－1，0）， ∴ 9 3 0, 1 0. b c b c         解得 2, 3. b c    ∴抛物线的解析式为 2 2 3y x x    ． 解法二：抛物线的解析式为 ( 3)( 1)y x x    ．[来~*@源:中国教育出^版#网] （2）抛物线的顶点坐标为（1，4）． 【方法指导】此题考查了用待定系数法求函数的解析式，用到的知识点是二次函数的解析式的形式，关键 是根据题意选择合适的解析式．[中国教*育&#^@出版网] 15．（2013 重庆，25，12 分）如图，已知抛物线 cbxxy  2 的图象与 x 轴的一个交点为 B（5，0），另 一个交点为 A，且与 y 轴交于点 C(0，5)． （1）求直线 BC 与抛物线的解析式； （2）若点 M 是抛物线在 x 轴下方图象上的一动点，过点 M 作 MN∥y 轴交直线 BC 于点 N，求 MN 的最大 值； （3）在（2）的条件下，MN 取得最大值时，若点 P 是抛物线在 x 轴下方图象上任意一点，以 BC 为边作平 行四边形 CBPQ，设平行四边形 CBPQ 的面积为 1S ，△ABN 的面积为 2S ，且 21 6SS  ，求点 P 的坐标． 【思路分析】（1）根据图象上的点的坐标用待定系数法解答；（2）设 M，N 两点的横坐标为一个未知数， 结合 M，N 两点所在函数的图形和解析式，把其纵坐标用该未知数表示，然后根据 MN⊥x 轴，MN 的长度 等于两点纵坐标的差，得到一个 MN 的长是所设未知数的函数，求出该函数的最大值即可；（3）首先可以 结合图形求出 2S 的值，再求出 1S 的值，求出平行四边形 CBPQ 的 BC 边上的高，求出直线 PQ 的解析式，最 后求出直线 PQ 与抛物线的交点，即得点 P 的坐标． 【解】（1）设直线 BC 的解析式为 bkxy  ，将 B（5，0），C（0，5）代入，得      5 05 b bk 解得      5 1 b k [中^国教育出版&#网~@] ∴直线 BC 的解析式为 5 xy ． 将 B（5，0），C（0，5）代入 cbxxy  2 ，得      5 0525 c cb 解得      5 6 c b ∴抛物线的解析式为 562  xxy ． （2）如图①，设点 M 的坐标为（x， 562  xx ），则 N 的坐标为（x， 5x ），[来源#*:中国%教育出~&版网] MN= )56()5( 2  xxx [来#% 源:&~中教网^] = xx 52  [中~&国^教育出#版网@] = 4 25)2 5( 2  x ， 当 2 5x 时，MN 最大值为 4 25 ． [www.z#&zste^p~.co@m] （3）如图②，当 0562  xxy 时，解得 11 x ， 52 x ，[w#&w%w@.zz~step.com] 故 A（1，0），B（5，0），∴AB=4． 把 2 5x 代入 5 xy ，得 52 5 y ， ∴点 N 的坐标为（ 2 5 ， 2 5 ）， ∴ 52 542 1 2  ABNSS ，∴ 306 21  SS ． 由 B（5，0），C（0，5）可得 OB=OC=5，BC= 25 ， 过点 C 作 CD⊥PQ 于 D，可得平行四边形 CBPQ 的 BC 边上的高 CD= 23 25 30  ． 设直线 PQ 交 y 轴于点 E，由 OB=OC，可得∠BCO=45°，∠DCE=45°，[来源:z#z@step.&co%m*] ∴CE=6，点 E 的坐标为（0，－1），∴直线 PQ 的解析式为 y=x－1． ∵点 P 同时在抛物线和直线 PQ 上，[来源:^@中教网&~%] ∴由 1562  xxx ，解得 21 x ， 32 x ∴P 点坐标为 P1（2，－3），P2 （3，－4）． 【方法指导】本题考查了用待定系数法求二次函数和一次函数的解析式以及二次函数和一次函数的性质， 建立数学模型求二次函数的最大值问题，考查了二次函数与几何图形的综合应用．用待定系数法求函数解 析式，一般来说，有几个待定系数就需要找出几个点的坐标；求线段、周长、面积等的最大值或最小值问 题，首先需考虑建立怎样的数学模型，使问题转化为求函数的极值问题；解答二次函数与几何问题的综合 问题时，需要用到解答几何证明问题的一些思考方法，比如“两头凑”就是思考和解决数学问题的重要而常 见的方法． 16．（2013 江西南昌，25，12 分）已知抛物线抛物线 y n=－(x－an)2+an（n 为正整数，且 00， ∴a1=1， 即 y1=―(x―1)2+1 方法一：令 y1=0 代入得：―(x―1)2+1=0， ∴x1=0，x2=2， ∴y1 与 x 轴交于 A0（0，0），A1（2，0） ∴b1=2， [www.*zz%step.#~co^m] 方法二：∵y1=―(x―a1)2+a1 与 x 轴交于点 A0（0，0）， ∴―(b1―1)2+1=0，b1=2 或 0，b1=0（舍去），[来*源%:zz#step&@.com] ∴b1=2， 又∴抛物线 y2=―(x―a2)2+a2 与 x 轴交于点 A1（2，0）， ∴―(2―a2)2+ a2=0，[中国#教^*~育出版&网] ∴a2=1 或 4，∵a2> a1，∴a2=1（舍去）， ∴取 a2=4，抛物线 y2=―(x―4)2+4． （2）（9，9）； （n2，n2） [来源:zzs#*t~e%^p.com] y=x． 详解如下： ∵抛物线 y2=―(x―4)2+4 令 y2=0 代入得：―(x―4)2+4=0， ∴x1=2，x2=6， ∴y2 与 x 轴交于点 A1（2，0），A2（6，0）， 又∵抛物线 y3=―(x―a3)2+a3 与 x 轴交于 A2（6，0），[来%源:@z~&z#step.com] ∴―(6―a3)2+a3=0 ∴a3=4 或 9，∵a3> a3，∴a3=4（舍去）， 只取 a3=9，招物线 y3 的顶点坐标为（9，9）， ∵由 y1 的顶点坐标为（1，1），y2 的顶点坐标为（4，4），抛物线 y3 的的顶点坐标为（9，9）， 依次类推抛物线 yn 的顶点坐标为（n2，n2）． ∵所有抛物线的顶点的横坐标等于纵坐标， ∴顶点坐标满足的函数关系式是：y= x；[来%源#:@中教&^网] ③∵A0（0，0），A1（2，0）， ∴A0 A1=2， 又∵yn=―(x―n2)2+n2， 令 yn=0， ∴―(x―n2)2+n2=0， 即 x1=n2+n，x2=n2－n， ∴A n－1(n2－n，0)，A n(n2+n，0)，即 A n－1 A n=( n2+n)－( n2－n)=2 n [来源:@~%*中国教育出版网#] ②存在， 是平行于 y=x 且过 A1（2，0）的直线，其表达式为 y=x－2． 【方法指导】本题考查了二次函数的一般知识，求字母系数、解析式、顶点坐标；字母表示数（符号意识）， 数形结合思想，规律探究，合情推理，解题方法的灵活性等等，更重要的是一种胆识和魄力，敢不敢动手， 会不会从简单，从特殊值入手去探究一般规律，画一画图帮助思考，所有这些都是做学问所必需的品质和 素养，也是新课程改革所倡导的精神和最高境界． 17.（2013 江苏泰州，26，14 分）已知：关于 x 的二欠函数 2 ( 0)y x ax a    ，点 1( , )A n y ， 2( 1, )B n y ， 3( 2, )C n y 都在这个二次函数的图象上，其中 n 为正整数. (1)若 1 2y y ，请说明 a 必为奇数， (2)设 a=11，求使 1 2 3y y y  成立的所有 n 的值; (3)对于给定的正实数 a，是否存在 n，使△ABC 是以 AC 为底边的等腰三角形?如果存在，求 n 的值(用 含 a 的代数式表示)；如果不存在，请说明理由.[来源:#z~zste*p.%co&m] 【思路分析】（1）根据 1 2y y 推出 2 1a n  ；（2）当 a=11 时，有 1 2 3y y y  ，根据增减性，求出 n 的 取值范围；（3）假设存在,则 AB=BC，进一步分析，得 1 12n a  . 【解】(1) )若 1 2y y ，则 2 2( 1) ( 1)n an n a n       即： 2 1a n  ∴a 必为奇数.[来%源~&:中*教@网] (2) 当 a=11 时，∵ 1 2 3y y y  [来&源:z*zstep.co@~m%] ∴ 2 2 211 ( 1) 11( 1) ( 2) 11( 2)n n n n n n            化简得： 0 2 10 4 18n n      解得： 4n  ∵n 为正整数.[中国教&^~育出#*版网] ∴ n  1、2、3、4. 关于 x 的二欠函数 2 ( 0)y x ax a    ，点 1( , )A n y ， 2( 1, )B n y ， 3( 2, )C n y 都在这个二次函数 的图象上，其中 n 为正整数. (3)假设存在,则 AB=BC ∴ 2 2 2 2 2 2 2 2(( 1) ) (( ( 1) ( 1)) ( )) (( 2) ( 1)) ((( ( 2) ( 2)) (( ( 1) ( 1)))n n n a n n an n n n a n n a n                        即：两边平方得： 2 2 2 2 2 2 2 2(( 1) ) (( ( 1) ( 1)) ( )) (( 2) ( 1)) ((( ( 2) ( 2)) (( ( 1) ( 1)))n n n a n n an n n n a n n a n                        化简得: 2 2 2 2 2 2(( ( 1) ( 1)) ( )) ((( ( 2) ( 2)) (( ( 1) ( 1)))n a n n an n a n n a n                 [中国#&教育出*版~@网] 2 2( 2 1 ) ( 2 3 )n a n a       ∴ 1 12n a  【方法指导】本题考查了二次函数的图象与性质、不等式、代数式、等腰三角形等知识综合运用. 18．（2013 广东广州，25，14 分）已知抛物线 cbxaxy  2 1 （a≠0,a≠c）过点 A(1,0)，顶点为 B，且抛 物线不经过第三象限。 （1）使用 a、c 表示 b; （2）判断点 B 所在象限，并说明理由； （3）若直线 mxy  22 经过点 B，且与该抛物线交于另一点 C( 8, ba c ),求当 x≥1 时 1y 的取值范围。 【思路分析】对于（1），把点 A（1,0）代入函数式，变形，即可得到b a c   ；对于（2），有多种思路 可以判断点在哪个象限，思路一：根据题意画图，由条件可知图像不经过第三象限就可以推出开口向上， 即 0a  ，由△可以判断出与 x 轴有两个交点，所以其顶点在第四象限；思路二：直接用公式法（或十字 相乘法）算出，抛物线与 x 轴有两个不同的交点的横坐标，分别为 1 21, ,( )cx x a ca    ，所以确定抛物 线顶点在第四象限；对于（3），题目问 1x  时， 1y 的取值范围，只要把图像画出来就清晰了，难点在于 要观察出 ( , 8)cC ba  是抛物线与 x 轴的另一个交点。因为抛物线与 x 轴有两个不同的交点的横坐标是 1 21, ,( )cx x a ca    ，由这里可以发现， 8 0, 8, 8,b b a c      还可以发现 C 在 A 的右侧；可以确 定直线经过 B、C 两点；看图像可以得到， 1x  时， 1y 大于等于最小值，此时算出二次函数最小值即可， 即求出 24 4 ac b a  即可，已经知道 8, 8,b a c    ，算出 ,a c 即可，即是要再找出一个与 ,a c 有关的式子， 即可解方程组求出 ,a c ；直线经过 B、C 两点，把 B、C 两点坐标代入直线消去 m ，整理即可得到 4c a  ， 联立 8a c  ，解得 6, 2c a  ，此时 2 1 4 24 ac by a    ． 【解】（1）把点 A（1,0）代入函数即可得到b a c   ．[来~源:zzs&tep.*co#%m] （2）若 a＜0，则抛物线开口向下，抛物线必过第三象限，所以，a＜0 不成立。 当 0a  时，抛物线开口向上，B 在第四象限。理由如下 由题意， 02  cbxax 可变形为 0)(2  cxcaax 解得 1 21, ,cx x a ca    所以抛物线与 x 轴有两个交点 又因为抛物线不经过第三象限[来源~@^:*zzstep.co&m] 所以 0a  ，且顶点在第四象限 （3）∵ ( , 8)cC ba  在抛物线上， ∴ 8 0, 8, 8,b b a c      把 B、C 两点代入直线解析式 mxy  22 ，[中国#&@教育出^版*网] 得 4c a  解得 6, 2c a  ∴ 682 2 1  xxy 抛物线的对称轴为 2x ∴当 1x  时， 1y 的最小值为顶点纵坐标，且无最大值， 即 2 1 4 24 ac by a    【方法指导】二次函数的问题通常都是其解析式、求对称轴、求顶点坐标、求最值以及与其他知识的综合 等，本题基本上综合了上述各种问题，解题的方法就是牢牢抓住二次函数的对称轴的求法，顶点坐标的求 法，以及最值的求法．[来&源~^:@中教网*] 19．（2013 山东德州,24,12 分）如图，在直角坐标系中有一直角三角形 AOB，O 为坐标原点，OA=1，tan ∠BAO=3，将此三角形绕原点 O 逆时针旋转 900，得到△DOC。抛物线 y=ax2+bx+c 经过点 A、B、C。 （1）求抛物线的解析式； （2）若点 P 是第二象限内抛物线上的动点，其横坐标为 t。 ①设抛物线对称轴 l 与 x 轴交于一点 E，连接 PE，交 CD 于 F。求出当△CEF 与△COD 相似时点 P 的坐标； ②是否存在一点 P，使△PCD 的面积最大？若存在，求出△PCD 面积的最大值；若不存在，请说明理由。 [中国教@育出版#~^网*] 【思路分析】（1）用待定系数法求出抛物线解析式；（2）求动点 P 坐标，需要进行探究，分类讨论存在情 况，结合相似、列一元二次方程解题；要探究使△PCD 的面积最大，寻求 PN=PM－NM，S△PCD＝△PCN+△ PND 列出二次函数模型来解决. 【解】（1）在 Rt△AOB 中，OA＝1，tan∠BAO=3 ∵tan∠BAO= OB OA ∴OB＝OA·tan∠BAO＝3 ∵△DOC 是由△AOB 绕原点 O 逆时针旋转 900 而得到的。[www.~z#zste&*p%.com] ∴OC＝OB＝3，OD＝OA＝1 ∴A、B、C 三点的坐标分别为（1，0），（0，3），（－3，0） 代放抛物线解析式得，[来^源#:中教&~网%] a+b+c=0 c=3 9a－3b+c=0 解之得，a=－1,b=－2,c=3 ∴抛物线的解析式为：y=－x2－2x+3 （2）①抛物线 y=－x2－2x+3 的对称轴 l 为：x= a b 2  = －1 ∴E 点坐标为（－1，4） （ⅰ）当∠CEF＝900 时，△CEF∽△COD,此时点 P 在对称轴上，即点 P 为抛物线的顶点。坐标为（－1，4） （ⅱ）当∠CFE＝900 时，△CFE∽△COD。过点 P 做 PMCA 于 点 M，则△EFC ∽△EMP。于是， 3 1 OC DO FC EF MP EM , ∴MP=3EM. 即：－t2－2t+3=3(－1－t)。 整理得：t2－t－6=0 解之得：t1=－2,t2=－3（不合题意，舍去）。 所以此时点 P 的坐标为（－2，3） 所以当△CEF 与△COD 相似时点 P 的坐标分别为：（－1，4） 或（－2，3）。 ②设直线 CD 的解析式为：y=kx+m 则得：      1 03 m mk ，解之得：k= 3 1 ,m=1 所以直线 CD 的解析式为：y= 3 1 x+1 设 PM 与 CD 的交点为 N，则点 N 的坐标为（t, 3 1 t+1）. ∴ PN=PM－NM=－t2－2t+3－（ 3 1 t+1）＝－t2－ 3 7 t+2 则 S△PCD＝△PCN+△PND ＝ 2 1 PN×CM+ 2 1 PN×OM= 2 1 PN×(CM+OM)= 2 1 PN×OC ＝ 2 3 （－t2－ 3 7 t+2）＝－ 2 3 （t+ 6 7 ）2+ 24 121 ∴当 t＝－ 6 7 时，S△PCD 的最大值为 24 121 。[中%国教育出版^&@ 网*] 【方法指导】本题主要考查二次函数、一次函数与相似三角形、旋转等结合，具有较强探究性、同时融合 方程思想、分类讨论思想、函数建摸等.[来源:中#国教^@育出版*%网] 20．（2013 山东菏泽，21，10 分） 如图，三角形 ABC 是以 BC 为底边的等腰三角形，点 A，C 分别是一次函数 3 34y x   的图象与 y 轴、 x 轴的交点，点 B 在二次函数 21 8y x bx c   的图像上，且该二次函数图像上存在一点 D 使四边形 ABCD 能构成平行四边形. (1)试求 b，c 的值、并写出该二次函数表达式； (2)动点 P 从 A 到 D，同时动点 Q 从 C 到 A 都以每秒 1 个单位的速度运动，问:[来源:%^ 中教&@网#] ①当 P 运动到何处时，有 PQ⊥AC? ②当 P 运动到何处时，四边形 PDCQ 的面积最小?此时四边形 PDCQ 的面积是多少?[中国#~教育*出版@%网] x y OB A D C [来源:*中国教育出^版网@&#] 【思路分析】（1）可以求出点 A、B 坐标，联系等腰三角形、平行四边形在平面直角坐标系中求解 B、D 坐 标，根据代定系数法确定二次函数表达式；（2）运用相似、图形面积计算、二次函数最大（小）值的计算 等解决动态型问题.[中国教育&出^*@版网#] 【解】（1）由 3 34y x   令 0x  ，得 3y  ∴点 A（0,3）[来源:@^zz&st*ep#.com] 令 0y  ，得 4x  ∴点 C（4,0） ∵三角形 ABC 是以 BC 为底边的等腰三角形 ∴点 B（－4,0） 又∵四边形 ABCD 能构成平行四边形 ∴点 D 的坐标为（8,3） 将 B（－4,0）、D（8,3）代入二次函数 21 8y x bx c   得： 1 4b   ， 3c   故：该二次函数表达式 将 B（－4,0）、D（8,3）代入二次函数 21 8y x bx c   得： 1 4b   ， 3c   故：该二次函数表达式为 21 1 38 4y x x   ··········3 分. （2） P x y OB A D C Q ①设点 P 运动到 t 秒时，有 PQ⊥AC，此时 AP=t, CQ=t, AQ=5 t ， ∵PQ⊥AC，则有△APQ∽△CAO,∴ 5 5 4 t t ，解得 25 9t  即：当点 P 运动到距 A 点 25 9 个单位处，有 PQ⊥AC. ····6 分. ②∵ APQ ACDPDCQS S S △ △四边形 ,且 1= 8 3=122ACDS  △ ∴当△APQ 面积最大时，四边形 PDCQ 的面积最小. 当动点 P 运动 t 秒时 AP=t,CQ=t,AQ=5 t 设△APQ 底边 AP 上的高为 h 作 QH⊥AD 于 H，由△AQH∽△CAO 可得： （也可由∠HAQ=∠OCA 得 sin∠ HAQ=sin∠ OCA 得到） 5 3 5 h t ，∴ 3 (5 )5h t  ， ∴ 2 21 3 3 3 5 25(5 ) ( 5 ) [( ) ]2 5 10 10 2 4APQS t t t t t          △ 23 5 15( )10 2 8t    ∴当 5 2t  时， APQS△ 达到最大值15 8 ，此时 15 8112 8 8PDCQS   四边形 ， 故当点 P 运动到距 A 点 5 2 个单位处时，四边形 PDCQ 面积最小，最小值为 81 8 ······10 分. 为 21 1 38 4y x x   ··········3 分.[来源:中国^%@教育出版~网&] （2）①设点 P 运动到 t 秒时，有 PQ⊥AC，此时 AP=t, CQ=t, AQ=5 t ，[来源#:zzst*ep.~com@^] ∵PQ⊥AC，则有△APQ∽△CAO,∴ 5 5 4 t t ，解得 25 9t  即：当点 P 运动到距 A 点 25 9 个单位处，有 PQ⊥AC. ····6 分. ②∵ APQ ACDPDCQS S S △ △四边形 ,且 1= 8 3=122ACDS  △ ∴当△APQ 面积最大时，四边形 PDCQ 的面积最小. 当动点 P 运动 t 秒时 AP=t,CQ=t,AQ=5 t 设△APQ 底边 AP 上的高为 h 作 QH⊥AD 于 H，由△AQH∽△CAO 可得： （也可由∠HAQ=∠OCA 得 sin∠ HAQ=sin∠ OCA 得到） 5 3 5 h t ，∴ 3 (5 )5h t  ， ∴ 2 21 3 3 3 5 25(5 ) ( 5 ) [( ) ]2 5 10 10 2 4APQS t t t t t          △ 23 5 15( )10 2 8t    [来源@^:&%中~教网] ∴当 5 2t  时， APQS△ 达到最大值15 8 ，此时 15 8112 8 8PDCQS   四边形 ， 故当点 P 运动到距 A 点 5 2 个单位处时，四边形 PDCQ 面积最小，最小值为 81 8 ······10 分. 【方法指导】本题考查了二次函数、一次函数与三角形、四边形等知识的综合.第（1）问相对容易解决； （2）问从题型看呈现动态探究型问题解决，相对考虑的知识点较多，这与平时把握的知识技能、数学思 考等解题质量联系密切突现试题的选拔功能. 21．（2013 四川凉山州，23，8 分）先阅读以下材料，然后解答问题： 材料：将二次函数 2 2 3y x x    的图象向左平移 1 个单位，再向下平移 2 个单位，求平移后的抛物线 的解析式（平移后抛物线的形状不变）。[中@#国教育出~&版*网] 解：在抛物线 2 2 3y x x    图象上任取两点 A （0，3）、 B （1，4），由题意知：点 A 向左平移 1 个单 位得到 A（ 1 ，3），再向下平移 2 个单位得到 A （ 1 ，1）；点 B 向左平移 1 个单位得到 B（0，4）， 再向下平移 2 个单位得到 B （0，2）。 设平移后的抛物线的解析式为 2y x bx c    。 则点 A （ 1 ，1）， B （0，2）在抛物线上。 可得： 1 1 2 b c c       ，解得： 0 2 b c    。[ww~w.zz^%s#tep.co&m] 所以平移后的抛物线的解析式为： 2 2y x   。 根据以上信息解答下列问题： 将直线 2 3y x  向右平移 3 个单位，再向上平移 1 个单位，求平移后的直线的解析式。 【思路分析】要根据题中所给的信息去解决这个问题.先通过平移后的点的坐标,进而用代入法求出函数解 析式. [来*~源#:中国教育出版网&%] 【解】在直线 y=2x－3 上任取两点 A(0,－3),B(1,－1).由题意知:点 A 向右平移 3 个单位得 A′(3,－3),再向上平移 1 个单位得到 A″(3,－2). 点 B 向右平移 3 个单位得 B′(4,－1),再向上平移 1 个单位得到 B″(4,0). 设 平 移 后 的 直 线 的 解 析 式 为 y=kx+b(k ≠ 0), 则 A ″ (3, － 2), B ″ (4,0) 在 直 线 上 , 可 得 2 3k+b, 2, 0 4 , 8. k k b b           解得 所以平移后的直线的解析式为 y=2x－8. 【方法指导】信息题就是利用所给的信息或是新的解题方法去解决相应的问题，一般是要解决的问题就是 按照信息所给的解题方法去解决。 22．（2013 江西，24，12 分）已知抛物线抛物线 y n=-(x-an)2+an （n 为正整数，且 00， ∴a1=1， 即 y1=―(x―1)2+1 方法一：令 y1=0 代入得：―(x―1)2+1=0， ∴x1=0，x2=2，[来源#*:中~教&% 网] ∴y1 与 x 轴交于 A0（0，0），A1（2，0）[www^.z&zstep.co@~m%] ∴b1=2， 方法二：∵y1=―(x―a1)2+a1 与 x 轴交于点 A0（0，0）， ∴―(b1―1)2+1=0，b1=2 或 0，b1=0（舍去），[来@源:中教^%#网~] ∴b1=2， [来源:中#国教育~出版&*网^] 又∴抛物线 y2=―(x―a2)2+a2 与 x 轴交于点 A1（2，0）， ∴―(2―a2)2+ a2=0， ∴a2=1 或 4，∵a2> a1，∴a2=1（舍去）， ∴取 a2=4，抛物线 y2=―(x―4)2+4． [来源:*中国教育出^版网@&#] （2）（9，9）； [来#源:中&国*教^育出~版网] （n2，n2） y=x． [来源@:^&z%zstep#.com] 详解如下：[中国教育#出&% 版*^网] ∵抛物线 y2=―(x―4)2+4 令 y2=0 代入得：―(x―4)2+4=0， ∴x1=2，x2=6， ∴y2 与 x 轴交于点 A1（2，0），A2（6，0）， 又∵抛物线 y3=―(x―a3)2+a3 与 x 轴交于 A2（6，0）， ∴―(6―a3)2+a3=0[来#^源@:中国教育出版~网*] ∴a3=4 或 9，∵a3> a3，∴a3=4（舍去）， 只取 a3=9，招物线 y3 的顶点坐标为（9，9），[来源:%&zz~s*tep.@com] ∵由 y1 的顶点坐标为（1，1），y2 的顶点坐标为（4，4），抛物线 y3 的的顶点坐标为（9，9）， 依次类推抛物线 yn 的顶点坐标为（n2，n2）． ∵所有抛物线的顶点的横坐标等于纵坐标，[来源:中国教^育~出版网%@#] ∴顶点坐标满足的函数关系式是：y= x； ③∵A0（0，0），A1（2，0），[来源:&*^中教%网#] ∴A0 A1=2， 又∵yn=―(x―n2)2+n2， 令 yn=0， ∴―(x―n2)2+n2=0， 即 x1=n2+n，x2=n2－n， ∴A n－1(n2－n，0)，A n(n2+n，0)，即 A n－1 A n=( n2+n)－( n2－n)=2 n ②存在， 是平行于 y=x 且过 A1（2，0）的直线，其表达式为 y=x－2． 【方法指导】本题考查了二次函数的一般知识，求字母系数、解析式、顶点坐标；字母表示数（符号 意识），数形结合思想，规律探究，合情推理，解题方法的灵活性等等，更重要的是一种胆识和魄力，敢 不敢动手，会不会从简单，从特殊值入手去探究一般规律，画一画图帮助思考，所有这些都是做学问所必 需的品质和素养，也是新课程改革所倡导的精神和最高境界． 23．（2013 白银，28，12 分）如图，在直角坐标系 xOy 中，二次函数 y=x2+（2k﹣1）x+k+1 的图象与 x 轴相交于 O、A 两点．[中@国*教育%&出版#网][来源:zz~*s#t%^ep.com] （1）求这个二次函数的解析式； （2）在这条抛物线的对称轴右边的图象上有一点 B，使△AOB 的面积等于 6，求点 B 的坐标； （3）对于（2）中的点 B，在此抛物线上是否存在点 P，使∠POB=90°？若存在，求出点 P 的坐标，并求 出△POB 的面积；若不存在，请说明理由． [中%国教^育*&~出版网] 考点：二次函数综合题． 分析：（1）将原点坐标代入抛物线中即可求出 k 的值，也就得出了抛物线的解析式． （2）根据（1）得出的抛物线的解析式可得出 A 点的坐标，也就求出了 OA 的长，根 据△OAB 的面积可求出 B 点纵坐标的绝对值，然后将符合题意的 B 点纵坐标代入抛 物线的解析式中即可求出 B 点的坐标，然后根据 B 点在抛物线对称轴的右边来判断 得出的 B 点是否符合要求即可． （3）根据 B 点坐标可求出直线 OB 的解析式，由于 OB⊥OP，由此可求出 P 点的坐 标特点，代入二次函数解析式可得出 P 点的坐标．求△POB 的面积时，可先求出 OB， OP 的长度即可求出△BOP 的面积． 解答：解：①∵函数的图象与 x 轴相交于 O， ∴0=k+1， ∴k=﹣1， ∴y=x2﹣3x， ②假设存在点 B，过点 B 做 BD⊥x 轴于点 D， ∵△AOB 的面积等于 6， ∴AO•BD=6， 当 0=x2﹣3x， x（x﹣3）=0， 解得：x=0 或 3， ∴AO=3， ∴BD=4 即 4=x2﹣3x， 解得：x=4 或 x=﹣1（舍去）． 又∵顶点坐标为：（ 1.5，﹣2.25）． ∵2.25＜4， ∴x 轴下方不存在 B 点， ∴点 B 的坐标为：（4，4）； ③∵点 B 的坐标为：（4，4）， ∴∠BOD=45°，BO= =4 ， 当∠POB=90°， ∴∠POD=45°， 设 P 点横坐标为：﹣x，则纵坐标为：x2﹣3x， 即﹣x=x2﹣3x， 解得 x=2 或 x=0， ∴在抛物线上仅存在一点 P （2，﹣2）． ∴OP= =2 ， 使∠POB=90°， ∴△POB 的面积为： PO•BO=×4 ×2 =8． 点评：本题考查了二次函数解析式的确定、函数图象交点、图象面积求法等知识．利用已知 进行分类讨论得出符合要求点的坐标是解题关键． 24．（2013 兰州，28，10 分）如图，在平面直角坐标系 xOy 中，A、B 为 x 轴上两点，C、D 为 y 轴上的 两点，经过点 A、C、B 的抛物线的一部分 C1 与经过点 A、D、B 的抛物线的一部分 C2 组合成一条封 闭曲线，我们把这条封闭曲线成为“蛋线”．已知点 C 的坐标为（0，﹣ ），点 M 是抛物线 C2：y=mx2 ﹣2mx﹣3m（m＜0）的顶点． （1）求 A、B 两点的坐标； （2）“蛋线”在第四象限上是否存在一点 P，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大 值；若不存在，请说明理由； （3）当△BDM 为直角三角形时，求 m 的值． 考点：二次函数综合题．[来源:zzstep.^c%@om~*] 分析：（1）将 y=mx2﹣2mx﹣3m 化为交点式，即可得到 A、B 两点的坐标；[来#源~:中国*&教@育出版网][来%源@:~&zzste#p.com][ww@w.zzstep.&%com*#] （2）先用待定系数法得到抛物线 C1 的解析式，过点 P 作 PQ∥y 轴，交 BC 于 Q，用待定系数法得到 直线 BC 的解析式，再根据三角形的面积公式和配方法得到△PBC 面积的最大值； （3）先表示出 DM2，BD2，MB2，再分两种情况：①DM2+BD2=MB2 时；②DM2+MB2=BD2 时，讨论 即可求得 m 的值． 解答：解：（1）y=mx2﹣2mx﹣3m=m（x﹣3）（x+1），[来源~&:中教^@%网] ∵m≠0， ∴当 y=0 时，x1=﹣1，x2=3，[来@源~:中&#教网%] ∴A（﹣1，0），B（3，0）；[w%ww^.zzste&p.*c#om] （2）设 C1：y=ax2+bx+c，将 A、B、C 三点的坐标代入得： ， 解得 ，[来源^:*&@中~教网] 故 C1：y= x2﹣x﹣ ． 如图：过点 P 作 PQ∥y 轴，交 BC 于 Q， 由 B、C 的坐标可得直线 BC 的解析式为：y= x﹣ ， 设 P（x， x2﹣x﹣ ），则 Q（x， x﹣ ），[来源:zzs%te@p#&.co^m] PQ= x﹣ ﹣（ x2﹣x﹣ ）=﹣ x2+ x， S△PBC= PQ•OB= ×（﹣ x2+ x）×3=﹣ （x﹣ ）2+ ， 当 x= 时，S△PBC 有最大值，Smax= ，[中*国教%@育~出版^网] ×（ ）2﹣ ﹣ =﹣ ， P（ ，﹣ ）； （3）y=mx2﹣2mx﹣3m=m（x﹣1）2﹣4m，[来源:中%^国@教育出~版网&][来源:*zzste@p^.~com%] 顶点 M 坐标（1，﹣4m）， 当 x=0 时，y=﹣3m， ∴D（0，﹣3m），B（3，0），[中%国教&*^育出版@网][来源:中*国教育出版^网%~#] ∴DM2=（0﹣1）2+（﹣3m+4m）2=m2+1， MB2=（3﹣1）2+（0+4m）2=16m2+4， BD2=（3﹣0）2+（0+3m）2=9m2+9，[来源:中%教网@#~*] 当△BDM 为 Rt△时有：DM2+BD2=MB2 或 DM2+MB2 =BD2．[来#~&*源:中教^网][来源:学§科§网 Z§X§X§K] ①DM2+BD2=MB2 时有：m2+1+9m2+9=16m2+4， 解得 m=﹣1（∵m＜0，∴m=1 舍去）； ②DM2+MB2=BD2 时有：m2+1+16m2+4=19m2+9，[来@源:中*&国教%育#出版网][中%国教育出版^&@网*] 解得 m=﹣ （m= 舍去）． 综上，m=﹣1 或﹣ 时，△BDM 为直角三角形． 点评：考查了二次函数综合题，涉及的知识点有：抛物线的交点式，待定系数法求抛物线的解析式， 待定系数法求直线的解析式，三角形的面积公式，配方法的应用，勾股定理，分类思想的运用，综合 性较强，有一定的难度． [w#~@w&w.zzste*p.com] 25．（2013 年佛山市，24，10 分）如图①，已知抛物线 y=ax2+bx+c 经过点 A（0，3），B（3，0），C（4， 3）． （1）求抛物线的函数表达式； （2）求抛物线的顶点坐标和对称轴；[来源:中@国&教育出^#版网~] （3）把抛物线向上平移，使得顶点落在 x 轴上，直接写出两条抛物线、对称轴和 y 轴围成的图形的面积 S （图②中阴影部分）． 分析：（1）把点 A、B、C 代入抛物线解析式 y=ax2+bx+c 利用待定系数法求解即可；[ww#w.zzs%t&ep.^@com] （2）把抛物线解析式整理成顶点式形式，然后写出顶点坐标与对称轴即可；[来源~:*&中^@教网][www.%zzs@t^ep#*.com] （3）根据顶点坐标求出向上平移的距离，再根据阴影部分的面积等于平行四边形的面积，列式进行计算 即可得解． 解：（1）∵抛物线 y=ax2+bx+c 经过点 A（0，3），B（3，0），C（4，3），[中国^&教育*出%#版网][来源#:zzst^ep.~*com%] ∴ ，解得 ， 所以抛物线的函数表达式为 y=x2﹣4x+3； （2）∵y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线的顶点坐标为（2，﹣1），对称轴为直线 x=2； （3）如图，∵抛物线的顶点坐标为（2，﹣1），∴PP′=1， 阴影部分的面积等于平行四边形 A′APP′的面积， 平行四边形 A′APP′的面积=1×2=2，[来源:&中教*网#%~] ∴阴影部分的面积=2． [来源@:中国~#*教育&出版网] 点评：本题考查了待定系数法求二次函数解析式，二次函数的性质，二次函数图象与几何变换，（3）根据 平移的性质，把阴影部分的面积转化为平行四边形的面积是解题的关键． 26．（2013 广东珠海，22，9 分）如图，在平面直角坐标系 xOy 中，矩形 OABC 的边 OA、OC 分别在 y 轴和 x 轴的正半轴上，且长分别为 m、4m（m＞0），D 为边 AB 的中点，一抛物线 l 经过点 A、D 及点 M （﹣1，﹣1﹣m）．[来%&~源^:中#教网] （1）求抛物线 l 的解析式（用含 m 的式子表示）；[来#&%^源:@中教网] （2）把△OAD 沿直线 OD 折叠后点 A 落在点 A′处，连接 OA′并延长与线段 BC 的延长线交于点 E，若抛 物线 l 与线段 CE 相交，求实数 m 的取值范围； （3）在满足（2）的条件下，求出抛物线 l 顶点 P 到达最高位置时的坐标． [来源:@~中&^教*网][中~国教%@育*出版网&] 考点：二次函数综合题． 3481324 分析：（1）设抛物线 l 的解析式为 y=ax2+bx+c，将 A、D、M 三点的坐标代入，运用待定系数法即 可求解； （2）设 AD 与 x 轴交于点 M，过点 A′作 A′N⊥x 轴于点 N．根据轴对称及平行线的性质得出 DM=OM=x，则 A′M=2m﹣x，OA′=m，在 Rt△OA′M 中运用勾股定理求出 x，得出 A′点坐标， 运用待定系数法得到直线 OA′的解析式，确定 E 点坐标（4m，﹣3m），根据抛物线 l 与线段 CE 相交，列出关于 m 的不等式组，求出解集即可； （3）根据二次函数的性质，结合（2）中求出的实数 m 的取值范围，即可求解． 解答：解：（1）设抛物线 l 的解析式为 y=ax2+bx+c， 将 A（0，m），D（2m，m），M（﹣1，﹣1﹣m）三点的坐标代入， 得 ，解得 ， 所以抛物线 l 的解析式为 y=﹣x2+2mx+m； （2）设 AD 与 x 轴交于点 M，过点 A′作 A′N⊥x 轴于点 N． ∵把△OAD 沿直线 OD 折叠后点 A 落在点 A′处， ∴△OAD≌△OA′D，OA=OA′=m，AD=A′D=2m，∠OAD=∠OA′D=90°，∠ADO=∠A′DO， ∵矩形 OABC 中，AD∥OC， ∴∠ADO=∠DOM， ∴∠A′DO=∠DOM， ∴DM=OM． 设 DM=OM=x，则 A′M=2m﹣x， 在 Rt△OA′M 中，∵OA′2+A′M2=OM2， ∴m2+（2m﹣x）2=x2， 解得 x= m． ∵S△OA′M= OM•A′N= OA′•A′M， ∴A′N= = m， ∴ON= = m， ∴A′点坐标为（ m，﹣ m）， 易求直线 OA′的解析式为 y=﹣ x， 当 x=4m 时，y=﹣ ×4m=﹣3m， ∴E 点坐标为（4m，﹣3m）． 当 x=4m 时，﹣x2+2mx+m=﹣（4m）2+2m•4m+m=﹣8m2+m， 即抛物线 l 与直线 CE 的交点为（4m，﹣8m2+m）， ∵抛物线 l 与线段 CE 相交， ∴﹣3m≤﹣8m2+m≤0， ∵m＞0， ∴﹣3≤﹣8m+1≤0， 解得 ≤m≤ ； （3）∵y=﹣x2+2mx+m=﹣（x﹣m）2+m2+m， ≤m≤ ， ∴当 x=m 时，y 有最大值 m2+m， 又∵m2+m=（m+ ）2﹣ ， ∴当 ≤m≤ 时，m2+m 随 m 的增大而增大， ∴当 m= 时，顶点 P 到达最高位置，m2+m=（ ）2+ = ， 故此时抛物线 l 顶点 P 到达最高位置时的坐标为（ ， ）． 点评：本题是二次函数的综合题，其中涉及到运用待定系数法求一次函数、二次函数的解析式，轴 对称的性质，勾股定理，两个函数交点坐标的求法，二次函数、矩形的性质，解不等式组等 知识，综合性较强，有一定难度．（2）中求出 A′点的坐标是解题的关键． 27．（2013 广西钦州，26，12 分）如图，在平面直角坐标系中，O 为坐标原点，抛物线 y= x2+2x 与 x 轴 相交于 O、B，顶点为 A，连接 OA． （1）求点 A 的坐标和∠AOB 的度数；[来源:#z~zstep&.c%o*m] （2）若将抛物线 y= x2+2x 向右平移 4 个单位，再向下平移 2 个单位，得到抛物线 m，其顶点为点 C．连 接 OC 和 AC，把△AOC 沿 OA 翻折得到四边形 ACOC′．试判断其形状，并说明理由； （3）在（2）的情况下，判断点 C′是否在抛物线 y= x2+2x 上，请说明理由； （4）若点 P 为 x 轴上的一个动点，试探究在抛物线 m 上是否存在点 Q，使以点 O、P、C、Q 为顶点的四 边形是平行四边形，且 OC 为该四边形的一条边？若存在，请直接写出点 Q 的坐标；若不存在，请说明理 由． 考点：二次函数综合题． 3718684 专题：探究型． 分析：（1）由 y= x2+2x 得，y= （x﹣2）2﹣2，故可得出抛物线的顶点 A 的坐标，令 x2+2x=0 得出点 B 的坐标过点 A 作 AD⊥x 轴，垂足为 D，由∠ADO=90°可知点 D 的坐标，故 可得出 OD=AD，由此即可得出结论； （2）由题意可知抛物线 m 的二次项系数为 ，由此可得抛物线 m 的解析式过点 C 作 CE⊥x 轴，垂足为 E；过点 A 作 AF⊥CE，垂足为 F，与 y 轴交与点 H，根据勾股定 理可求出 OC 的长，同理可得 AC 的长，OC=AC，由翻折不变性的性质可知， OC=AC=OC′=AC′，由此即可得出结论； （3）过点 C′作 C′G⊥x 轴，垂足为 G，由于 OC 和 OC′关于 OA 对称， ∠AOB=∠AOH=45°，故可得出∠COH=∠C′OG，再根据 CE∥OH 可知 ∠OCE=∠C′OG，根据全等三角形的判定定理可知△CEO≌△C′GO，故可得出点 C′ 的坐标把 x=﹣4 代入抛物线 y= x2+2x 进行检验即可得出结论； （4）由于点 P 为 x 轴上的一个动点，点 Q 在抛物线 m 上，故设 Q（a， （a﹣2）2 ﹣4），由于 OC 为该四边形的一条边，故 OP 为对角线，由于点 P 在 x 轴上，根据中 点坐标的定义即可得出 a 的值，故可得出结论． 解答：解：（1）∵由 y= x2+2x 得，y= （x﹣2）2﹣2， ∴抛物线的顶点 A 的坐标为（﹣2，﹣2）， 令 x2+2x=0，解得 x1=0，x2=﹣4， ∴点 B 的坐标为（﹣4，0）， 过点 A 作 AD⊥x 轴，垂足为 D， ∴∠ADO=90°， ∴点 A 的坐标为（﹣2，﹣2），点 D 的坐标为（﹣2，0）， ∴OD=AD=2， ∴∠AOB=45°； （2）四边形 ACOC′为菱形． 由题意可知抛物线 m 的二次项系数为 ，且过顶点 C 的坐标是（2，﹣4）， ∴抛物线的解析式为：y= （x﹣2）2﹣4，即 y= x2﹣2x﹣2， 过点 C 作 CE⊥x轴，垂足为 E；过点 A 作 AF⊥CE，垂足为 F，与 y 轴交与点 H， ∴OE=2，CE=4，AF=4，CF=CE﹣EF=2， ∴OC= = =2 ， 同理，AC=2 ，OC=AC， 由反折不变性的性质可知，OC=AC=OC′=AC′， 故四边形 ACOC′为菱形． （3）如图 1，点 C′不在抛物线 y= x2+2x 上． 理由如下： 过点 C′作 C′G⊥x 轴，垂足为 G， ∵OC 和 OC′关于 OA 对称，∠AOB=∠AOH=45°， ∴∠COH=∠C′OG， ∵CE∥OH， ∴∠OCE=∠C′OG， 又∵∠CEO=∠C′GO=90°，OC=OC′， ∴△CEO≌△C′GO， ∴OG=4，C′G=2， ∴点 C′的坐标为（﹣4，2）， 把 x=﹣4 代入抛物线 y= x2+2x 得 y=0， ∴点 C′不在抛物线 y= x2+2x 上； （4）存在符合条件的点 Q． ∵点 P 为 x 轴上的一个动点，点 Q 在抛物线 m 上， ∴设 Q（a， （a﹣2）2﹣4）， ∵OC 为该四边形的一条边， ∴OP 为对角线， ∴ =0，解得 x1=6，x2=4， ∴P（6，4）或（﹣2，4）（舍去）， ∴点 Q 的坐标为（6，4）． 点评：本题考查的是二次函数综合题，涉及到抛物线的性质、菱形的判定与性质、平行四边 形的性质等知识，难度适中． 28．（2013 贵州安顺，26，10 分）如图，已知抛物线与 x 轴交于 A（﹣1，0），B（3，0）两点，与 y 轴交 于点 C（0，3）． （1）求抛物线的解析式； （2）设抛物线的顶点为 D，在其对称轴的右侧的抛物线上是否存在点 P，使得△PDC 是等腰三角形？若 存在，求出符合条件的点 P 的坐标；若不存在，请说明理由； （3）点 M 是抛物线上一点，以 B，C，D，M 为顶点的四边形是直角梯形，试求出点 M 的坐标．[www%.^z#zstep.co&m*] 考点：二次函数综合题． 专题：压轴题． 分析：（1）由于 A（﹣1，0）、B（3，0）、C（0，3）三点均在坐标轴上，故设一般式解答和设交点式（两 点式）解答均可． （2）分以 CD 为底和以 CD 为腰两种情况讨论．运用两点间距离公式建立起 P 点横坐标和纵坐标之间的关 系，再结合抛物线解析式即可求解．[www.z*^%z~step.co#m] （3）根据抛物线上点的坐标特点，利用勾股定理求出相关边长，再利用勾股定理的逆定理判断出直角梯 形中的直角，便可解答． 解答：解：（1）∵抛物线与 y 轴交于点 C（0，3）， ∴设抛物线解析式为 y=ax2+bx+3（a≠0）， 根据题意，得 ，[中国教育出版&网*^@%] 解得 ， ∴抛物线的解析式为 y=﹣x2+2x+3． （2）存在． 由 y=﹣x2+2x+3 得，D 点坐标为（1，4），对称轴为 x=1．[中国~@*教#育出&版网] ①若以 CD 为底边，则 PD=PC， 设 P 点坐标为（x，y），根据两点间距离公式，[中@国~教育出#&版*网] 得 x2+（3﹣y）2=（x﹣1）2+（4﹣y）2，[来源&#:~zzst@ep^.com] 即 y=4﹣x． 又 P 点（x，y）在抛物线上， ∴4﹣x=﹣x2+2x+3， 即 x2﹣3x+1=0， 解得 x1= ，x2= ＜1，应舍去， ∴x= ， ∴y=4﹣x= ， 即点 P 坐标为 ． ②若以 CD 为一腰，[来^源:zzst&~ep.c#om%] ∵点 P 在对称轴右侧的抛物线上，由抛物线对称性知，点 P 与点 C 关于直线 x=1 对称， 此时点 P 坐标为（2，3）． ∴符合条件的点 P 坐标为 或（2，3）． （3）由 B（3，0），C（0，3），D（1，4），根据勾股定理， 得 CB= ，CD= ，BD= ， ∴CB2+CD2=BD2=20， ∴∠BCD=90°，[来@源:z%zstep.&^co*m] 设对称轴交 x 轴于点 E，过 C 作 CM⊥DE，交抛物线于点 M，垂足为 F，在 Rt△DCF 中， ∵CF=DF=1，[中&国教%育出^@版~网] ∴∠CDF=45°， 由抛物线对称性可知，∠CDM=2×45°=90°，点坐标 M 为（2，3）， ∴DM∥BC，[w*ww.~z#zstep.c%o@m] ∴四边形 BCDM 为直角梯形， 由∠BCD=90°及题意可知，[来@源~:中&#教网%] 以 BC 为一底时，顶点 M 在抛物线上的直角梯形只有上述一种情况； 以 CD 为一底或以 BD 为一底，且顶点 M 在抛物线上的直角梯形均不存在． 综上所述，符合条件的点 M 的坐标为（2，3）．[来源~@:*^中国教育&出版网][www.zz&^st#ep.co*m~] 点评：此题是一道典型的“存在性问题”，结合二次函数图象和等腰三角形、等腰梯形的性质，考查了它们 存在的条件，有一定的开放性． [中&国^教育出#版~网@] 29．（（2013 贵州毕节，27，16 分）如图，抛物线 y=ax2+b 与 x 轴交于点 A、B，且 A 点的坐标为（1，0）， 与 y 轴交于点 C（0，1）．[w#ww.zz*step.com@^~] （1）求抛物线的解析式，并求出点 B 坐标；[来%源:@~z&zstep#.com] （2）过点 B 作 BD∥CA 交抛物线于点 D，连接 BC、CA、AD，求四边形 ABCD 的周长；（结果保留根号） [来#% 源:中国教育^&出版网@] （3）在 x 轴上方的抛物线上是否存在点 P，过点 P 作 PE 垂直于 x 轴，垂足为点 E，使以 B、P、E 为顶点 的三角形与△CBD 相似？若存在请求出 P 点的坐标；若不存在，请说明理由． [来源@:中#~国*教&育出版网] 考点：二次函数综合题． 分析：（1）利用待定系数法求出抛物线的解析式，点 B 坐标可由对称性质得到，或令 y=0， 由解析式得到； （2）关键是求出点 D 的坐标，然后利用勾股定理分别求出四边形 ABCD 四个边的长 度； （3）本问为存在型问题．可以先假设存在，然后按照题意条件求点 P 的坐标，如果 能求出则点 P 存在，否则不存在．注意三角形相似有两种情形，需要分类讨论． 解答：解：（1）∵点 A（1，0）和点 C（0，1）在抛物线 y=ax2+b 上， ∴ ，解得：a=﹣1，b=1， ∴抛物线的解析式为：y=﹣x2+1， 抛物线的对称轴为 y 轴，则点 B 与点 A（1，0）关于 y 轴对称，∴B（﹣1，0）． （2）设过点 A（1，0），C（0，1）的直线解析式为 y=kx+b，可得： ，解得 k=﹣1，b=1，∴y=﹣x+1． ∵BD∥CA，∴可设直线 BD 的解析式为 y=﹣x+n， ∵点 B（﹣1，0）在直线 BD 上，∴0=1+n，得 n=﹣1， ∴直线 BD 的解析式为：y=﹣x﹣1． 将 y=﹣x﹣1 代入抛物线的解析式，得：﹣x﹣1=﹣x2+1，解得：x1=2，x2=﹣1， ∵B 点横坐标为﹣1，则 D 点横坐标为 2， D 点纵坐标为 y=﹣2﹣1=﹣3，∴D 点坐标为（2，﹣3）． 如答图①所示，过点 D 作 DN⊥x 轴于点 N，则 DN=3，AN=1，BN=3， 在 Rt△BDN 中，BN=DN=3，由勾股定理得：BD= ； 在 Rt△ADN 中，DN=3，AN=1，由勾股定理得：AD= ； 又 OA=OB=OC=1，OC⊥AB，由勾股定理得：AC=BC= ； ∴四边形 ABCD 的周长为：AC+BC+BD+AD= + + + = + ． （3）假设存在这样的点 P，则△BPE 与△CBD 相似有两种情形： （I）若△BPE∽△BDC，如答图②所示， 则有 ，即 ，∴PE=3BE． 设 OE=m（m＞0），则 E（﹣m，0），BE=1﹣m，PE=3BE=3﹣3m， ∴点 P 的坐标为（﹣m，3﹣3m）． ∵点 P 在抛物线 y=﹣x2+1 上， ∴3﹣3m=﹣（﹣m）2+1，解得 m=1 或 m=2， 当 m=1 时，点 E 与点 B 重合，故舍去；当 m=2 时，点 E 在 OB 左侧，点 P 在 x 轴下 方，不符合题意，故舍去． 因此，此种情况不存在； （II）若△EBP∽△BDC，如答图③所示， 则有 ，即 ，∴BE=3PE． 设 OE=m（m＞0），则 E（m，0），BE=1+m，PE=BE=（1+m）=+m， ∴点 P 的坐标为（m， +m）． ∵点 P 在抛物线 y=﹣x2+1 上， ∴+m=﹣（m）2+1，解得 m=﹣1 或 m=， ∵m＞0，故 m=1 舍去，∴m=， 点 P 的纵坐标为： +m=+×=， ∴点 P 的坐标为（，）． 综上所述，存在点 P，使以 B、P、E 为顶点的三角形与△CBD 相似，点 P 的坐标为 （，）． 点评：本题是代数几何综合题，考查了二次函数的图象与性质、一次函数的图象与性质、待 定系数法、相似三角形的判定与性质、勾股定理等重要知识点．第（2）问的解题要 点是求出点 D 的坐标，第（3）问的解题要点是分类讨论． 30．（2013 湖北孝感，22，10 分）在“母亲节”前夕，我市某校学生积极参与“关爱贫困母亲”的活动，他们 购进一批单价为 20 元的“孝文化衫”在课余时间进行义卖，并将所得利润捐给贫困母亲．经试验发现，若每 件按 24 元的价格销售时，每天能卖出 36 件；若每件按 29 元的价格销售时，每天能卖出 21 件．假定每天 销售件数 y（件）与销售价格 x（元/件）满足一个以 x 为自变量的一次函数． （1）求 y 与 x 满足的函数关系式（不要求写出 x 的取值范围）； （2）在不积压且不考虑其他因素的情况下，销售价格定为多少元时，才能使每天获得的利润 P 最大？[来源&:% 中国教育出~版网#*] 考点：二次函数的应用；一次函数的应用． 分析：（1）设 y 与 x 满足的函数关系式为：y=kx+b．，由题意可列出 k 和 b的二元一次方程 组，解出 k 和 b 的值即可； （2）根据题意：每天获得的利润为：P=（﹣3x+108）（x﹣20），转换为 P=﹣3（x﹣28） 2+192，于是求出每天获得的利润 P 最大时的销售价格． 解答：解：（1）设 y 与 x 满足的函数关系式为：y=kx+b． 由题意可得： 解得 故 y 与 x 的函数关系式为：y=﹣3x+108． （2）每天获得的利润为：P=（﹣3x+108）（x﹣20）=﹣3x2+168x﹣2160=﹣3（x﹣28） 2+192． 故当销售价定为 28 元时，每天获得的利润最大． 点评：本题主要考查二次函数的应用的知识点，解答本题的关键是熟练掌握二次函数的性质 以及最值得求法，此题难度不大． 31（2013 湖北孝感，25，12 分）如图 1，已知正方形 ABCD 的边长为 1，点 E 在边 BC 上，若∠AEF=90°， 且 EF 交正方形外角的平分线 CF 于点 F．[中%&国教*育^出版~网] （1）图 1 中若点 E 是边 BC 的中点，我们可以构造两个三角形全等来证明 AE=EF，请叙述你的一个构造方 案，并指出是哪两个三角形全等（不要求证明）； （2）如图 2，若点 E 在线段 BC 上滑动（不与点 B，C 重合）． ①AE=EF 是否总成立？请给出证明； ②在如图 2 的直角坐标系中，当点 E 滑动到某处时，点 F 恰好落在抛物线 y=﹣x2+x+1 上，求此时点 F 的 坐标． [中@国教^育% 出版#*网] 考点：二次函数综合题． 专题：综合题． 分析：（1）取 AB 的中点 G，连接 EG，利用 SSS 能得到 △ AGE 与 △ ECF 全等； （2）①在 AB 上截取 AM=EC，证得 △ AME≌△ECF 即可证得 AE=EF； ②过点 F 作 FH⊥x 轴于 H，根据 FH=BE=CH 设 BH=a，则 FH=a﹣1，然后表示出点 F 的 坐标，根据点 F 恰好落在抛物线 y=﹣x2+x+1 上得到有关 a 的方程求得 a 值即可求得点 F 的坐标； 解答：（1）解：如图 1，取 AB 的中点 G，连接 EG． △ AGE 与 △ ECF 全等． （2）①若点 E 在线段 BC 上滑动时 AE=EF 总成立． 证明：如图 2，在 AB 上截取 AM=EC． ∵AB=BC， ∴BM=BE， ∴△MBE 是等腰直角三角形， ∴∠AME=180°﹣45°=135°， 又∵CF 平分正方形的外角， ∴∠ECF=135°， ∴∠AME=∠ECF． 而∠BAE+∠AEB=∠CEF+∠AEB=90°， ∴∠BAE=∠CEF， ∴△AME≌△ECF． ∴AE=EF． ②过点 F 作 FH⊥x 轴于 H， 由①知，FH=BE=CH， 设 BH=a，则 FH=a﹣1， ∴点 F 的坐标为 F（a，a﹣1） ∵点 F 恰好落在抛物线 y=﹣x2+x+1 上， ∴a﹣1=﹣a2+a+1， ∴a2=2， （负值不合题意，舍去）， ∴ ． ∴点 F 的坐标为 ． 点评：本题考查了二次函数的综合知识，题目中涉及到了全等的知识，还渗透了方程思想， 是一道好题． [来源*#:%中&教^网] 32．（2013 湖北宜昌，22，12 分）如图 1，平面之间坐标系中，等腰直角三角形的直角边 BC 在 x 轴正半轴 上滑动，点 C 的坐标为（t，0），直角边 AC=4，经过 O，C 两点做抛物线 y1=ax（x﹣t）（a 为常数，a＞0）， 该抛物线与斜边 AB 交于点 E，直线 OA：y2=kx（k 为常数，k＞0） [来源@^&:%zzste#p.com] （1）填空：用含 t 的代数式表示点 A 的坐标及 k 的值：A （t，4） ，k= （k＞0） ； （2）随着三角板的滑动，当 a= 时： ①请你验证：抛物线 y1=ax（x﹣t）的顶点在函数 y= 的图象上； ②当三角板滑至点 E 为 AB 的中点时，求 t 的值； （3）直线 OA 与抛物线的另一个交点为点 D，当 t≤x≤t+4，|y2﹣y1|的值随 x 的增大而减小，当 x≥t+4 时， |y2﹣y1|的值随 x 的增大而增大，求 a 与 t 的关系式及 t 的取值范围． [来源&:zzs#t~ep.c*@om] 考点：二次函数综合题． 3718684 分析：（1）根据题意易得点 A 的横坐标与点 C 的相同，点 A 的纵坐标即是线段 AC 的长度； 把点 A 的坐标代入直线 OA 的解析式来求 k 的值； （2）①求得抛物线 y1 的顶点坐标，然后把该坐标代入函数 y= ，若该点满足 函数解析式 y= ，即表示该顶点在函数 y= 图象上；反之，该顶点不在函 数 y= 图象上； ②如图 1，过点 E 作 EK⊥x 轴于点 K．则 EK 是 △ ACB 的中位线，所以根据三角形中位 线定理易求点 E 的坐标，把点 E 的坐标代入抛物线 y1= x（x﹣t）即可求得 t=2； （3）如图 2，根据抛物线与直线相交可以求得点 D 横坐标是 +4．则 t+4= +4，由 此可以求得 a 与 t 的关系式． 解答：解：（1）∵点 C 的坐标为（t，0），直角边 AC=4， ∴点 A 的坐标是（t，4）． 又∵直线 OA：y2=kx（k 为常数，k＞0）， ∴4=kt，则 k= （k＞0）． （2）①当 a= 时，y1= x（x﹣t），其顶点坐标为（ ，﹣ ）． 对于 y= 来说，当 x= 时，y= × =﹣ ，即点（ ，﹣ ）在抛物线 y= 上． 故当 a= 时，抛物线 y1=ax（x﹣t）的顶点在函数 y= 的图象上； ②如图 1，过点 E 作 EK⊥x 轴于点 K． ∵AC⊥x 轴， ∴AC∥EK． ∵点 E 是线段 AB 的中点， ∴K 为 BC 的中点， ∴EK 是 △ ACB 的中位线， ∴EK= AC=2，CK= BC=2， ∴E（t+2，2）． ∵点 E 在抛物线 y1= x（x﹣t）上， ∴ （t+2）（t+2﹣t）=2， 解得 t=2． （3）如图 2， ，则 x=ax（x﹣t）， 解得 x= +4，或 x=0（不合题意，舍去）．． 故点 D 的横坐标是 +t． 当 x= +t 时，|y2﹣y1|=0，由题意得 t+4= +t， 解得 a= （t＞0）． 点评：本题考查了坐标与图形的性质、二次函数图象上点的坐标特征、一次函数与二次函数 交点坐标等知识点．解题时，注意“数形结合”数学思想的应用． 33．[2013 湖南邵阳，25，8 分]如图(二)所示，已知抛物线 y = -2x2 -4x 的图象 E，将其向右平移两个单位 后得到抛物线 F. (1)求抛物线 F 所表示的解析式； (2)设抛物线 F 和 x 轴相交于点 O、点 B(点 B 位于点 O 的右侧)，顶点为 C.点 A 位于 y 轴负半轴上，且到 x 轴的距离等于点 C 到 x 轴距离的 2 倍，求 AB 所在直线的解析式. [来%&~源^:中@教网] [来源:中国%教育出版@#~*网] [www.z@%z~step.^com*] [来&源#%:中^*教网] 知识考点：二次函数图象的平移，二次函数与一次函数结合. 审题要津：（1）将二次函数解析式变换为顶点式，在根据二次函数图象左加右减，上加下减的平移规律进行 解答；（2）利用待定系数法求一次函数解析式. 满分解答：解：(1)∵y=-2x2 -4x = -2(x2+2x) =-2(x +1)2 +2. ∴将抛物线 y =-2x2 -4x 向右平移两个单位后的解析式为 y =-2(x +1-2)2 +2，即 y=-2x2 +4x.[w~w&w.zz*ste%^p.com] (2)解方程-2x2 +4x =0，得 x1=0，x2=4. ∴O(0,0),B(4,0). ∵y=-2(x-1)2 +2， ∴C(1,2)，所以点 C 到 x 轴的距离为 2. ∴点 A 到 x 轴的距离为 4， ∵点 A 在 y 轴的负半轴上， ∴A(0，-4). 设直线 AB 的解析式为 y=kx+c， ∴有 4k+b=0 b=4 ，解得 k=-1 b=4 . ∴直线 AB 的解析式为 y= -x +4. 名师点评：本题考查了二次函数图象的平移，一次函数解析式的确定，解题的关键是求出 F 图象的解析式.[中 国教育出版@^&网*#] 34．（2013 湖南郴州，25，10 分）如图，△ABC 中，AB=BC，AC=8，tanA=k，P 为 AC 边上一动点，设 PC=x，作 PE∥AB 交 BC 于 E，PF∥BC 交 AB 于 F． （1）证明： △ PCE 是等腰三角形； （2）EM、FN、BH 分别是 △ PEC、 △ AFP、 △ ABC 的高，用含 x 和 k 的代数式表示 EM、FN，并探究 EM、FN、 BH 之间的数量关系； （3）当 k=4 时，求四边形 PEBF 的面积 S 与 x 的函数关系式．x 为何值时，S 有最大值？并求出 S 的最大值． 考点：等腰三角形的判定与性质；二次函数的最值；解直角三角形． 3718684 分析：（1）根据等边对等角可得∠A=∠C，然后根据两直线平行，同位角相等求出∠CPE= ∠A，从而得到∠CPE=∠C，即可得证； （2）根据等腰三角形三线合一的性质求出 CM= CP，然后求出 EM，同理求出 FN、 BH 的长，再根据结果整理可得 EM+FN=BH； （3）分别求出 EM、FN、BH，然后根据 S △ PCE，S △ APF，S △ ABC，再根据 S=S △ ABC﹣S △ PCE ﹣S △ APF，整理即可得到 S 与 x 的关系式，然后利用二次函数的最值问题解答． 解答：（1）证明：∵AB=BC， ∴∠A=∠C， ∵PE∥AB， ∴∠CPE=∠A， ∴∠CPE=∠C， ∴△PCE 是等腰三角形； （2）解：∵△PCE 是等腰三角形，EM⊥CP， ∴CM= CP= ，tanC=tanA=k， ∴EM=CM•tanC= •k= ， 同理：FN=AN•tanA= •k=4k﹣ ， 由于 BH=AH•tanA= ×8•k=4k， 而 EM+FN= +4k﹣ =4k， ∴EM+FN=BH； （3）解：当 k=4 时，EM=2x，FN=16﹣2x，BH=16， 所以，S △ PCE= x•2x=x2，S △ APF= （8﹣x）•（16﹣2x）=（8﹣x）2，S △ ABC= ×8×16=64， S=S △ ABC﹣S △ PCE﹣S △ APF， =64﹣x2﹣（8﹣x）2， =﹣2x2+16x， 配方得，S=﹣2（x﹣4）2+32， 所以，当 x=4 时，S 有最大值 32． 点评：本题考查了等腰三角形的判定与性质，平行线的性质，锐角三角函数，二次函数的最 值问题，表示出各三角形的高线是解题的关键，也是本题的难点． 35 ．（2013 湖南娄底，24，10 分）（2013•娄底）已知：一元二次方程 x2+kx+k﹣=0．[来源:中国%^@教*育~出版网] （1）求证：不论 k 为何实数时，此方程总有两个实数根； （2）设 k＜0，当二次函数 y=x2+kx+k﹣的图象与 x 轴的两个交点 A、B 间的距离为 4 时，求此二次函数的 解析式； （3）在（2）的条件下，若抛物线的顶点为 C，过 y 轴上一点 M（0，m）作 y 轴的垂线 l，当 m 为何值时， 直线 l 与 △ ABC 的外接圆有公共点？ 考点：二次函数综合题． 3718684 分析：（1）根据一元二次方程的根的判别式 △ =b2﹣4ac 的符号来判定已知方程的根的情况； （2）利用根与系数的关系（|xA﹣xB|= =4）列出关于 k 的 方程，通过解方程来求 k 的值； （3）根据直线与圆的位置的位置关系确定 m 的取值范围． 解答：（1）证明：∵△=k2﹣4××（k﹣）=k2﹣2k+1=（k﹣1）2≥0， ∴关于 x 的一元二次方程 x2+kx+k﹣=0，不论 k 为何实数时，此方程总有两个实数根； （2）令 y=0，则 x2+kx+k﹣=0． ∵xA+xB=﹣2k，xA•xB=2k﹣1， ∴|xA﹣xB|= = =2|k﹣1|=4，即|k﹣1|=2， 解得 k=3（不合题意，舍去），或 k=﹣1． ∴此二次函数的解析式是 y=x2﹣x﹣； （3）由（2）知，抛物线的解析式是 y=x2﹣x﹣． 易求 A（﹣1，0），B（3，0），C（1，﹣2）， ∴AB=4，AC=2 ，BC=2 ． 显然 AC2+BC2=AB2，得 △ ABC 是等腰直角三角形．AB 为斜边， ∴外接圆的直径为 AB=4， ∴﹣2≤m≤2． 点评：本题综合考查了二次函数综合题，其中涉及到的知识点有：抛物线与 x 轴的交点，待 定系数法求二次函数的解析式以及直线与圆的关系，范围较广，难度较大． 36. （2013 江苏南京，26，9 分） 已知二次函数 y=a(xm)2a(xm) (a、m 为常数，且 a0)。 (1) 求证：不论 a 与 m 为何值，该函数的图像与 x 轴总有两个公共点； (2) 设该函数的图像的顶点为 C，与 x 轴交于 A、B 两点，与 y 轴交于点 D。  当△ABC 的面积等于 1 时，求 a 的值：  当△ABC 的面积与△ABD 的面积相等时，求 m 的值。 解析： (1) 证明：y=a(xm)2a(xm)=ax2(2ama)xam2am。 因为当 a0 时，[(2ama)]24a(am2am)=a2>0。 所以，方程 ax2(2ama)xam2am=0 有两个不相等的实数根。[来~源&:中国% 教育^*出版网] 所以，不论 a 与 m 为何值，该函数的图像与 x 轴总有两个公共点。(3 分)[中国%教&育*@出版~网] (2) 解： y=a(xm)2a(xm)=(x 2m1 2 )2 a 4 ，[来%#源*:中^&教网] 所以，点 C 的坐标为( 2m1 2 , a 4 )。[w~^%w#w.zz*step.com] 当 y=0 时，a(xm)2a(xm)=0。解得 x1=m，x2=m1。所以 AB=1。 当△ABC 的面积等于 1 时， 1 2 1|  a 4 |=1。 所以 1 2 1(  a 4 )=1，或 1 2 1 a 4 =1。[来源:^*中&%教网@] 所以 a=8，或 a=8。  当 x=0 时，y=am2am，所以点 D 的坐标为(0, am2am)。 当△ABC 的面积与△ABD 的面积相等时， 1 2 1|  a 4 |= 1 2 1| am2am |。[中%&国教*育^出版~网][来&源^:%@中*教网] 所以 1 2 1(  a 4 )= 1 2 1(am2am)，或 1 2 1 a 4 = 1 2 1(am2am)。 所以 m= 1 2 ，或 m= 1 2 2 ，或 m= 1 2 2 。 (9 分)[来源:%中*#国教~育出^版网][来#源:z~zstep*.co&m%] 37（2013 湖南张家界，25，12 分）如图，抛物线 y=ax2+bx+c（a≠0）的图象过点 C（0，1），顶点为 Q（2， 3），点 D 在 x 轴正半轴上，且 OD=OC． （1）求直线 CD 的解析式； （2）求抛物线的解析式； （3）将直线 CD 绕点 C 逆时针方向旋转 45°所得直线与抛物线相交于另一点 E，求证： △ CEQ∽△CDO； （4）在（3）的条件下，若点 P 是线段 QE 上的动点，点 F 是线段 OD 上的动点，问：在 P 点和 F 点移动 过程中， △ PCF 的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由． 考点：二次函数综合题． 3718684 分析：（1）利用待定系数法求出直线解析式； （2）利用待定系数法求出抛物线的解析式； （3）关键是证明 △ CEQ 与 △ CDO 均为等腰直角三角形； （4）如答图②所示，作点 C 关于直线 QE 的对称点 C′，作点 C 关于 x 轴的对称点 C″， 连接 C′C″，交 OD 于点 F，交 QE 于点 P，则 △ PCF 即为符合题意的周长最小的三角形， 由轴对称的性质可知， △ PCF 的周长等于线段 C′C″的长度． 利用轴对称的性质、两点之间线段最短可以证明此时 △ PCF 的周长最小． 如答图③所示，利用勾股定理求出线段 C′C″的长度，即 △ PCF 周长的最小值． 解答：解：（1）∵C（0，1），OD=OC，∴D 点坐标为（1，0）． 设直线 CD 的解析式为 y=kx+b（k≠0）， 将 C（0，1），D（1，0）代入得： ， 解得：b=1，k=﹣1， ∴直线 CD 的解析式为：y=﹣x+1． （2）设抛物线的解析式为 y=a（x﹣2）2+3， 将 C（0，1）代入得：1=a×（﹣2）2+3，解得 a= ． ∴y= （x﹣2）2+3= x2+2x+1． （3）证明：由题意可知，∠ECD=45°， ∵OC=OD，且 OC⊥OD，∴△OCD 为等腰直角三角形，∠ODC=45°， ∴∠ECD=∠ODC，∴CE∥x 轴，则点 C、E 关于对称轴（直线 x=2）对称， ∴点 E 的坐标为（4，1）． 如答图①所示，设对称轴（直线 x=2）与 CE 交于点 F，则 F（2，1）， ∴ME=CM=QM=2，∴△QME 与 △ QMC 均为等腰直角三角形，∴∠QEC=∠QCE=45°． 又∵△OCD 为等腰直角三角形，∴∠ODC=∠OCD=45°， ∴∠QEC=∠QCE=∠ODC=∠OCD=45°， ∴△CEQ∽△CDO． （4）存在． 如答图②所示，作点 C 关于直线 QE 的对称点 C′，作点 C 关于 x 轴的对称点 C″，连接 C′C″，交 OD 于点 F，交 QE 于点 P，则 △ PCF 即为符合题意的周长最小的三角形，由轴 对称的性质可知， △ PCF 的周长等于线段 C′C″的长度． （证明如下：不妨在线段 OD 上取异于点 F 的任一点 F′，在线段 QE 上取异于点 P 的 任一点 P′，连接 F′C″，F′P′，P′C′． 由轴对称的性质可知， △ P′CF′的周长=F′C″+F′P′+P′C′； 而 F′C″+F′P′+P′C′是点 C′，C″之间的折线段， 由两点之间线段最短可知：F′C″+F′P′+P′C′＞C′C″， 即 △ P′CF′的周长大于 △ PCE 的周长．） 如答图③所示，连接 C′E， ∵C，C′关于直线 QE 对称， △ QCE 为等腰直角三角形， ∴△QC′E 为等腰直角三角形， ∴△CEC′为等腰直角三角形， ∴点 C′的坐标为（4，5）； ∵C，C″关于 x 轴对称，∴点 C″的坐标为（﹣1，0）． 过点 C′作 C′N⊥y 轴于点 N，则 NC′=4，NC″=4+1+1=6， 在 Rt △ C′NC″中，由勾股定理得：C′C″= = = ． 综上所述，在 P 点和 F 点移动过程中， △ PCF 的周长存在最小值，最小值为 ． 点评：本题是中考压轴题，综合考查了二次函数的图象与性质、待定系数法、相似三角形、 等腰直角三角形、勾股定理、轴对称的性质等重要知识点，涉及考点较多，有一点的 难度．本题难点在于第（4）问，如何充分利用轴对称的性质确定 △ PCF 周长最小时的 几何图形，是解答本题的关键． 38．（2013·聊城，25，?分）已知△ABC 中，边 BC 的长与 BC 边上的高的和为 20． （1）写出△ABC 的面积 y 与 BC 的长 x 之间的函数关系式，并求出面积为 48 时 BC 的长；[中%国教育@出&#版网*] （2）当 BC 多长时，△ABC 的面积最大？最大面积是多少？[中国教&^~育#出*版网] （3）当△ABC 面积最大时，是否存在其周长最小的情形？如果存在，请说出理由，并求出其最小周长； 如果不存在，请给予说明．[来源~:zzst%ep.c*&#om] 考点：二次函数综合题． 分析：（1）先表示出 BC 边上的高，再根据三角形的面积公式就可以表示出表示 y 与 x 之间的函数关系式， 当 y＝48 时代入解析式就可以求出其值； （2）将（1）的解析式转化为顶点式就可以求出最大值．[来#*源~:&中教^网] （3）由（2）可知△ABC 的面积最大时，BC＝10，BC 边上的高也为 10 过点 A 作直线 L 平行于 BC， 作点 B 关于直线 L 的对称点 B′，连接 B′C 交直线 L 于点 A′，再连接 A′B，AB′，根据轴对称的性质及 三角形的周长公式就可以求出周长的最小值．[中&国教育出版@*#%网] 解答：解：（1）由题意，得 y＝ ＝－ x2＋10x， 当 y＝48 时，－ x2＋10x＝48， 解得：x1＝12，x2＝8，[来~源:%中教∴面积为 48 时 BC 的长为 12 或 8；[来源:中教^网%@*&] （2）∵y＝－ x2＋10x，∴y＝－ （x－10）2＋50，[来源:%中*&教网@~]∴当 x＝10 时，y 最大＝50； （3）△ABC 面积最大时，△ABC 的周长存在最小的情形．理由如下：由（2）可知△ABC 的面积最大时， BC＝10，BC 边上的高也为 10，[中国教育出@&^版~网*] 过点 A 作直线 L 平行于 BC，作点 B 关于直线 L 的对称点 B′， 连接 B′C 交直线 L 于点 A′，再连接 A′B，AB′ 则由对称性得：A′B′＝A′B，AB′＝AB， ∴A′B＋A′C＝A′B′＋A′C＝B′C， 当点 A 不在线段 B′C 上时，则由三角形三边关系可得： △ABC 的周长＝AB＋AC＋BC＝AB′＋AC＋BC＞B′C＋BC， 当点 A 在线段 B′C 上时，即点 A 与 A′重合， 这时△ABC 的周长＝AB＋AC＋BC＝A′B′＋A′C＋BC＝B′C＋BC， 因此当点 A 与 A′重合时，△ABC 的周长最小； 这时由作法可知：BB′＝20，∴B′C＝ ＝10 ，∴△ABC 的周长＝10 ＋10，[中%^@国教&育出~版网] 因此当△ABC 面积最大时，存在其周长最小的情形，最小周长为 10 ＋10．[中~国教%@育&出版网*][中^国&%教#育出版网*] [中国教育出@&^版~网*] 点评：本题是一道二次函数的综合试题，考查了二次函数的解析式的运用，一元二次方程的解法和顶点式 的运用，轴对称的性质的运用，在解答第三问时灵活运用轴对称的性质是关键． [www&.%zzstep~*.c@om] 39（2013·泰安，29，?分）如图，抛物线 y＝ x2＋bx＋c 与 y 轴交于点 C（0，－4），与 x 轴交于点 A， B，且 B 点的坐标为（2，0） （1）求该抛物线的解析式． （2）若点 P 是 AB 上的一动点，过点 P 作 PE∥AC，交 BC 于 E，连接 CP，求△PCE 面积的最大值． （3）若点 D 为 OA 的中点，点 M 是线段 AC 上一点，且△OMD 为等腰三角形，求 M 点的坐标． 考点：二次函数综合题． 分析：（1）利用待定系数法求出抛物线的解析式； （2）首先求出△PCE 面积的表达式，然后利用二次函数的性质求出其最大值； （3）△OMD 为等腰三角形，可能有三种情形，需要分类讨论． 解答：解：（1）把点 C（0，－4），B（2，0）分别代入 y＝ x2＋bx＋c 中， 得 ，解得 ∴该抛物线的解析式为 y＝ x2＋x－4．[来源~@^:*中国教育&出版网] （2）令 y＝0，即 x2＋x－4＝0，解得 x1＝－4，x2＝2， ∴A（－4，0），S△ABC＝ AB•OC＝12． 设 P 点坐标为（x，0），则 PB＝2－x．[来源^:中~#& 教*网] ∵PE∥AC，∴∠BPE＝∠BAC，∠BEP＝∠BCA，∴△PBE∽△ABC， ∴ ，即 ，化简得：S△PBE＝ （2－x）2．[ww~w.zzs%#t@ep.^com] S△PCE＝S△PCB－S△PBE＝ PB•OC－S△PBE＝ ×（2－x）×4－ （2－x）2 ＝ x2－ x＋ ＝ （x＋1）2＋3 ∴当 x＝－1 时，S△PCE 的最大值为 3． （3）△OMD 为等腰三角形，可能有三种情形：（I）当 DM＝DO 时，如答图①所示．[ww&w.~z*zs#tep.co@m] DO＝DM＝DA＝2，[来@#源:中国教~& 育出*版网] ∴∠OAC＝∠AMD＝45°， ∴∠ADM＝90°，∴M 点的坐标为（－2，－2）；[来~源:&zzstep.co#m@^] （II）当 MD＝MO 时，如答图②所示． 过点 M 作 MN⊥OD 于点 N，则点 N 为 OD 的中点， ∴DN＝ON＝1，AN＝AD＋DN＝3，[中国教育*出&%^#版网] 又△AMN 为等腰直角三角形，∴MN＝AN＝3， ∴M 点的坐标为（－1，－3）； （III）当 OD＝OM 时，[来#源:中%&教网*^] ∵△OAC 为等腰直角三角形，[来源:学科网] ∴点 O 到 AC 的距离为 ×4＝ ，即 AC 上的点与点 O 之间的最小距离为 ． ∵ ＞2，∴OD＝OM 的情况不存在． 综上所述，点 M 的坐标为（－2，－2）或（－1，－3）．[来源#:*中国教%育出~&版网][来源:中#国&*教育出@版~网] 点评：本题是二次函数综合题，考查了二次函数的图象与性质、待定系数法、相似三角形、等腰三角形等 知识点，以及分类讨论的数学思想．第（2）问将面积的最值转化为二次函数的极值问题，注意其中求面 积表达式的方法；第（3）问重在考查分类讨论的数学思想，注意三种可能的情形需要一一分析，不能遗 漏． [中国*教育^#出&版网%][ 来源:zzstep%.c#@o*&m] 40．（2013·鞍山，26，10 分）如图，已知一次函数 y＝0.5x+2 的图象与 x 轴交于点 A，与二次函数 y＝ax2+bx+c 的图象交于 y 轴上的一点 B，二次函数 y＝ax2+bx+c 的图象与 x 轴只有唯一的交点 C，且 OC＝2．[中国*教育%&出版#网@] （1）求二次函数 y＝ax2+bx+c 的解析式；[来#%源:&~中教网^] （2）设一次函数 y＝0.5x+2 的图象与二次函数 y＝ax2+bx+c 的图象的另一交点为 D，已知 P 为 x 轴上的一 个动点，且△PBD 为直角三角形，求点 P 的坐标．[来%源:中国教&育出版网^@#] 考点：二次函数综合题．[来源:z^zste&p#.c~o*m] 分析：（1）根据 y＝0.5x+2 交 x 轴于点 A，与 y 轴交于点 B，即可得出 A，B 两点坐标，二次函数 y＝ax2+bx+c 的图象与 x 轴只有唯一的交点 C，且 OC＝2．得出可设二次函数 y＝ax2+bx+c＝a（x－2）2，进而求出即 可；[来源#~@:z*zstep&.com] （2）根据当 B 为直角顶点，当 D 为直角顶点，以及当 P 为直角顶点时，分别利用三角形相似对应边成比 例求出即可．[来源^:*&@中~教网] 解答：解：（1）∵y＝0.5x+2 交 x 轴于点 A，∴0＝0.5x+2，∴x＝－4，[中国教#*育&出版^网@] 与 y 轴交于点 B， ∵x＝0，∴y＝2∴B 点坐标为：（0，2），∴A（－4，0），B（0，2）， ∵二次函数 y＝ax2+bx+c 的图象与 x 轴只有唯一的交点 C，且 OC＝2[中~#国教育出&版^网%] 把 B（0，2）代入得：a＝0.5[来%源*:中^&教网#] ∴二次函数的解析式：y＝0.5x2－2x+2； （2）（Ⅰ）当 B 为直角顶点时，过 B 作 BP1⊥AD 交 x 轴于 P1 点由 Rt△AOB∽Rt△BOP1∴ ＝ ， ∴ ＝ ，[来源:中国%教育出版@#~*网]得：OP1＝1，∴P1（1，0）， （Ⅱ）作 P2D⊥BD，连接 BP2， 将 y＝0.5x+2 与 y＝0.5x2－2x+2 联立求出两函数交点坐标：D 点坐标为：（5，4.5）， 则 AD＝ ， 当 D 为直角顶点时[来@源%:中*^~教网] ∵∠DAP2＝∠BAO，∠BOA＝∠ADP2，∴△ABO∽△AP2D，∴ ＝ ， ＝ ，[解得：AP2＝11.25，则 OP2＝11.25－4＝7.25， 故 P2 点坐标为（7.25，0）； （Ⅲ）当 P 为直角顶点时，过点 D 作 DE⊥x 轴于点 E，设 P3（a，0） 则由 Rt△OBP3∽Rt△EP3D[来源:*~&%中^教网] 得： ，∴ ，[来#~*& 源:中教^网] ∵方程无解，∴点 P3 不存在， ∴点 P 的坐标为：P1（1，0）和 P2（7.25，0）． [来源:*^中国#教~育出版网@] 点评：此题主要考查了二次函数综合应用以及求函数与坐标轴交点和相似三角形的与性质等知识，根据已 知进行分类讨论得出所有结果，注意不要漏解． [来@&源:中*国教育出版网#~] 41．（2013•徐州，26，8 分）如图，在 Rt△ABC 中，∠C＝90°，翻折∠C，使点 C 落在斜边 AB 上某一点 D 处，折痕为 EF（点 E、F 分别在边 AC、BC 上）[来源:中国教育^出%#版&网@] （1）若△CEF 与△ABC 相似． ①当 AC＝BC＝2 时，AD 的长为 ； ②当 AC＝3，BC＝4 时，AD 的长为 1．8 或 2．5 ；[来^&*源:中@教%网] （2）当点 D 是 AB 的中点时，△CEF 与△ABC 相似吗？请说明理由． [来~源#:%zzs@te^p．com] 考点：相似三角形的判定与性质；翻折变换（折叠问题）． 分析：（1）若△CEF 与△ABC 相似． ①当 AC＝BC＝2 时，△ABC 为等腰直角三角形；[中国教#育^出@版网*&] ②当 AC＝3，BC＝4 时，分两种情况： （I）若 CE：CF＝3：4，如答图 2 所示，此时 EF∥AB，CD 为 AB 边上的高； （II）若 CF：CE＝3：4，如答图 3 所示．由相似三角形角之间的关系，可以推出∠A＝∠ECD 与∠B＝ ∠FCD，从而得到 CD＝AD＝BD，即 D 点为 AB 的中点； （2）当点 D 是 AB 的中点时，△CEF 与△ABC 相似．可以推出∠CFE＝∠A，∠C＝∠C，从而可以证明 两个三角形相似． 解答：解：（1）若△CEF 与△ABC 相似． ①当 AC＝BC＝2 时，△ABC 为等腰直角三角形，如答图 1 所示． 此时 D 为 AB 边中点，AD＝ AC＝ ． ②当 AC＝3，BC＝4 时，有两种情况： （I）若 CE：CF＝3：4，如答图 2 所示． ∵CE：CF＝AC：BC，∴EF∥BC． 由折叠性质可知，CD⊥EF，∴CD⊥AB，即此时 CD 为 AB 边上的高．[来源:中@教^网*&%] 在 Rt△ABC 中，AC＝3，BC＝4，∴BC＝5，∴cosA＝． AD＝AC•cosA＝3×＝1．8； （II）若 CF：CE＝3：4，如答图 3 所示． ∵△CEF∽△CAB，∴∠CEF＝∠B． 由折叠性质可知，∠CEF＋∠ECD＝90°，[www&.zz~*st#ep.com@] 又∵∠A＋∠B＝90°，[来源:z@&zstep.#^c%om] ∴∠A＝∠ECD，∴AD＝CD． 同理可得：∠B＝∠FCD，CD＝BD， ∴此时 AD＝AB＝×5＝2．5． 综上所述，当 AC＝3，BC＝4 时，AD 的长为 1．8 或 2．5． （2）当点 D 是 AB 的中点时，△CEF 与△ABC 相似．理由如下：[中国%#教&育出^版*网] 如答图 3 所示，连接 CD，与 EF 交于点 Q． ∵CD 是 Rt△ABC 的中线，∴CD＝DB＝AB，∴∠DCB＝∠B． 由折叠性质可知，∠CQF＝∠DQF＝90°，∴∠DCB＋∠CFE＝90°， ∵∠B＋∠A＝90°，∴∠CFE＝∠A， 又∵∠C＝∠C，∴△CEF∽△CBA． 点评：本题是几何综合题，考查了几何图形折叠问题和相似三角形的判定与性质．第（1）②问需要分两 种情况分别计算，此处容易漏解，需要引起注意． 42．（2013•徐州，27，10 分）为增强公民的节约意识，合理利用天然气资源，某市自 1 月 1 日起对市区民 用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：[来源~:中教^*网&%] 每月用气量 单价（元/m3） 不超出 75m3 的部分 2．5 超出 75m3 不超出 125m3 的部分 a 超出 125m3 的部分 a＋0．25 （1）若甲用户 3 月份的用气量为 60m3，则应缴费 150 元； （2）若调价后每月支出的燃气费为 y（元），每月的用气量为 x（m3），y 与 x 之间的关系如图所示，求 a 的值及 y 与 x 之间的函数关系式；[www.zz&^s#tep.co*m~] （3）在（2）的条件下，若乙用户 2、3 月份共用 1 气 175m3（3 月份用气量低于 2 月份用气量），共缴费 455 元，乙用户 2、3 月份的用气量各是多少？[来源~&:中教^@%网] [www．z#@zs%tep．^com*] 考点：一次函数的应用． 分析：（1）根据单价×数量＝总价就可以求出 3 月份应该缴纳的费用；[www.#z&zst%e~p.c@om] （2）结合统计表的数据）根据单价×数量＝总价的关系建立方程就可以求出 a 值，再从 0≤x≤75，75＜x≤125 和 x＞125 运用待定系数法分别表示出 y 与 x 的函数关系式即可； （3）设乙用户 2 月份用气 xm3，则 3 月份用气（175－x）m3，分 3 种情况：x＞125，175－x≤75 时，75 ＜x≤125，175－x≤75 时，当 75＜x≤125，75＜175－x≤125 时分别建立方程求出其解就可以． 解答： 解：（1）由题意，得 60×2．5＝150（元）； （2）由题意，得 a＝（325－75×2．5）÷（125－75）， a＝2．75，∴a＋0．25＝3， 设 OA 的解析式为 y1＝k1x，则有 2．5×75＝75k1，∴k1＝2．5， ∴线段 OA 的解析式为 y1＝2．5x（0≤x≤75）； 设线段 AB 的解析式为 y2＝k2x＋b，由图象，得 ，解得： ， ∴线段 AB 的解析式为：y2＝2．75x－18．75（75＜x≤125）；[ww~w.zzs@t^ep&.#com] （385－325）÷3＝20，故 C（145，385），设射线 BC 的解析式为 y3＝k3x＋b1，由图象，得 ， 解得： ， ∴射线 BC 的解析式为 y3＝3x－50（x＞125） （3）设乙用户 2 月份用气 xm3，则 3 月份用气（175－x）m3， 当 x＞125，175－x≤75 时， 3x－50＋2．5（175－x）＝455， 解得：x＝135，175－135＝40，符合题意； 当 75＜x≤125，175－x≤75 时， 2．75x－18．75＋2．5（175－x）＝455， 解得：x＝145，不符合题意，舍去； 当 75＜x≤125，75＜175－x≤125 时， 2．75x－18．75＋2．75（175－x）＝455，此方程无解． ∴乙用户 2、3 月份的用气量各是 135m3，40m3． 点评： 本题是一道一次函数的综合试题，考查了单价×数量＝总价的运用，待定系数法求一次函数的解 析式的运用，分段函数的运用，分类讨论思想在解实际问题的运用，解答时求出函数的解析式是关键． 43．（2013•徐州，28，10 分）如图，二次函数 y＝x2＋bx－的图象与 x 轴交于点 A（－3，0）和点 B，以 AB 为边在 x 轴上方作正方形 ABCD，点 P 是 x 轴上一动点，连接 DP，过点 P 作 DP 的垂线与 y 轴交于点 E． （1）请直接写出点 D 的坐标： （－3，4） ； （2）当点 P 在线段 AO（点 P 不与 A、O 重合）上运动至何处时，线段 OE 的长有最大值，求出这个最大 值；[中*@国&教%育出版~网] （3）是否存在这样的点 P，使△PED 是等腰三角形？若存在，请求出点 P 的坐标及此时△PED 与正方形 ABCD 重叠部分的面积；若不存在，请说明理由． 考点： 二次函数综合题． 分析： （1）将点 A 的坐标代入二次函数的解析式求得其解析式，然后求得点 B 的坐标即可求得正方形 ABCD 的边长，从而求得点 D 的纵坐标； （2）PA＝t，OE＝l，利用△DAP∽△POE 得到比例式，从而得到有关两个变量的二次函数，求最值即可； [来%源:中教#~网^&] （3）分点 P 位于 y 轴左侧和右侧两种情况讨论即可得到重叠部分的面积． 解答：解：（1）（－3，4）； （2）设 PA＝t，OE＝l， 由∠DAP＝∠POE＝∠DPE＝90°得△DAP∽△POE， ∴ ， ∴l＝－ ＋ ＝－（t－）2＋ ∴当 t＝时，l 有最大值 ， 即 P 为 AO 中点时，OE 的最大值为 ；[来源:*^ 中国#教~育出版网@] （3）存在． ①点 P 点在 y 轴左侧时，P 点的坐标为（－4，0） 由△PAD∽△OEG 得 OE＝PA＝1，∴OP＝OA＋PA＝4。 ∵△ADG∽△OEG，∴AG：GO＝AD：OE＝4：1[来源&%:#中国教育出版~网*] ∴AG＝ ＝ [来*源%:z#zstep&.co^m] ∴重叠部分的面积＝ ＝ ②当 P 点在 y 轴右侧时，P 点的坐标为（4，0）， 此时重叠部分的面积为 点评： 本题考查了二次函数的综合知识，与二次函数的最值结合起来，题目的难度较大． [中国教育出版网*~&%@] 44．（2013·鞍山，18，2 分）某商场购进一批单价为 4 元的日用品．若按每件 5 元的价格销售，每月能卖 出 3 万件；若按每件 6 元的价格销售，每月能卖出 2 万件，假定每月销售件数 y（件）与价格 x（元/件） 之间满足一次函数关系． （1）试求 y 与 x 之间的函数关系式； （2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？ 考点：二次函数的应用． 分析：（1）利用待定系数法求得 y 与 x 之间的一次函数关系式；[来源:中*@教网&#~] （2）根据“利润＝（售价－成本）×售出件数”，可得利润 W 与销售价格 x 之间的二次函数关系式，然后求 出其最大值．[来源:~@中国^#教育% 出版网] 解答：解：（1）由题意，可设 y＝kx+b，[w#ww.zzs%~@tep^.com] 把（5，30000），（6，20000）代入得： ，解得： ， 所以 y 与 x 之间的关系式为：y＝－10000x+80000；[来源*:#中%国~教@育出版网] （2）设利润为 W，则 W＝（x－4）（－10000x+80000）[ ＝－10000（x－4）（x－8）＝－10000（x2－12x+32）＝－10000[（x－6）2－4 ] ＝－10000（x－6）2+40000 所以当 x＝6 时，W 取得最大值，最大值为 40000 元． 答：当销售价格定为 6 元时，每月的利润最大，每月的最大利润为 40000 元． 点评：本题主要考查利用函数模型（二次函数与一次函数）解决实际问题的能力．要先根据题意列出函数 关系式，再代数求值．解题关键是要分析题意根据实际意义求解．注意：数学应用题来源于实践用于实践， 在当今社会市场经济的环境下，应掌握一些有关商品价格和利润的知识． 45．（2013•东营，24，12 分）已知抛物线 y=ax2+bx+c 的顶点 A（2，0），与 y 轴的交点为 B（0，－1）．[来源^:*&@中~教网] AO （第 24 题图） x y B (1)求抛物线的解析式；[来源~:*^中国教育%出#版网] (2)在对称轴右侧的抛物线上找出一点 C，使以 BC 为直径的圆经过抛物线的顶点 A．并求出点C 的坐标以及 此时圆的圆心 P 点的坐标． (3)在（2）的基础上，设直线 x=t（00 时 y 值随 x 值增大而减小的是（ ）． A．y = x2 B．y = x－１ C． y = 3 4 x D．y = 1 x 【答案】D 3. （2011 湖北鄂州，15，3 分）已知函数         2 2 1 1 3 5 1 3 x x y x x       ≤ ＞ ，则使 y=k 成立的 x 值恰好有三个，则 k 的值为（ ） A．0 B．1 C．2 D．3 4. （2011 山东德州 6,3 分）已知函数 ))(( bxaxy  （其中 a b ）的图象 如下面右图所示，则函数 baxy  的图象可能正确的是 第 6 题图 y x 1 1O （A） y x 1 -1 O （B） y x -1 -1 O （C） 1 -1 x y O （D） 【答案】D 5. （2011 山东菏泽，8，3 分）如图为抛物线 2y ax bx c   的图像，A、B、C 为抛物线与坐标轴的交点， 且 OA=OC=1，则下列关系中正确的是 A．a＋b=－1 B． a－b=－1 C． b<2a D． ac<0 【答案】B 6. （2011 山东泰安，20 ，3 分）若二次函数 y=ax2+bx+c 的 x 与 y 的部分对应值如下表： X -7 -6 -5 -4 -3 -2 y -27 -13 -3 3 5 3 则当 x=1 时，y 的值为 A.5 B.-3 C.-13 D.-27 【答案】D 7. （2011 山东威海，7，3 分）二次函数 2 2 3y x x   的图象如图所示．当 y＜0 时，自变量 x 的取值范 围是（ ）． A．－1＜x＜3 B．x＜－1 C． x＞3 D．x＜－1 或 x＞3 【答案】A 8. （2011 山东烟台，10,4 分）如图，平面直角坐标系中，两条抛物线有相同的对称轴，则下列关系正确 的是（ ） A．m＝n，k＞h B．m＝n ，k＜h C．m＞n，k＝h D．m＜n，k＝h 【答案】A 9. （2011 浙江温州，9，4 分）已知二次函数的图象(0≤x≤3)如图所示．关于该函数在所给自变量取值范围 内，下列说法正确的是( ) A．有最小值 0，有最大值 3 B．有最小值－1，有最大值 0 C．有最小值－1，有最大值 3 D．有最小值－1，无最大值 【答案】D 10．（2011 四川重庆，7，4 分）已知抛物线 y＝ax2＋bx＋c(a≠0)在平面直角坐标系中的位置如图所示，则 下列结论中正确的是( ) A． a>0 B． b＜0 C． c＜0 D． a＋b＋c>0 【答案】D 11. （2011 台湾台北，6）若下列有一图形为二次函数 y＝2x2－8x＋6 的图形，则此图为何？ 【答案】A 12. （2011 台湾台北，32）如图(十四)，将二次函数 22 8999931 ＋－＝ xxy 的图形画在坐标平面上，判断 方程 式 08999931 22 ＝＋－ xx 的两根，下列叙述何者正确？ A．两根相异，且均为正根 B．两根相异，且只有一个正根 C．两根相同，且为正根 D．两根相同，且为负根 【答案】A 13. （2011 台湾全区，28）图(十二)为坐标平面上二次函数 cbxaxy  2 的图形，且此图形通（－1 , 1）、（2 ,－1）两点．下列关于此二次函数的叙述，何者正确？ A ．y 的最大值小于 0 B．当 x＝0 时，y 的值大于 1 C．当 x＝1 时，y 的值大于 1 D．当 x＝3 时，y 的值小于 0 【答案】Ｄ 14. （2011 甘肃兰州，5，4 分）抛物线 2 2 1y x x   的顶点坐标是 A．（1，0） B．（－1，0） C．（－2，1） D．（2，－1） 【答案】A 15. （2011 甘肃兰州，9，4 分）如图所示的二次函数 2y ax bx c   的图象中，刘星同学观察得出了下 面四条信息：（1） 2 4 0b ac  ；（2）c>1；（3）2a－b<0；（4）a+b+c<0。你认为其中错误．．的有 A．2 个 B．3 个 C．4 个 D．1 个 x y -1 1O 1 【答案】D 16. （2011 江苏宿迁,8,3 分）已知二次函数 y＝ax2＋bx＋c（a≠0）的图象如图，则下列结论中正确的是（▲） A．a＞0 B．当 x＞1 时，y 随 x 的增大而增大 C．c＜0 D．3 是方程 ax2＋bx＋c＝0 的一个根 【答案】D 17. （2011 山东济宁，8，3 分）已知二次函数 2y ax bx c   中，其函数 y 与自变量 x 之间的部分对 应值如下表所示： x …… 0 1 2 3 4 …… y …… 4 1 0 1 4 …… 点 A（ 1x ， 1y ）、B（ 2x ， 2y ）在函数的图象上，则当 11 2,x  23 4x  时， 1y 与 2y 的大小关系正 确的是 A． 1 2y y B． 1 2y y C． 1 2y y D． 1 2y y 【答案】B 18. （2011 山东聊城，9，3 分）下列四个函数图象中，当 x<0 时，函数值 y 随自变量 x 的增大而减小的是 （ ） 【答案】D 19. （2011 山东潍坊，12，3 分）已知一元二次方程 2 0 ( 0)ax bx c a     的两个实数根 1x 、 2x 满足 1 2 4x x  和 1 2 3x x  ，那么二次函数 2 ( 0)y ax bx c a     的图象有可能是（ ） 【答案】C 20．（2011 四川广安，10，3 分）若二次函数 2( ) 1y x m   ．当 x ≤l 时， y 随 x 的增大而减小，则 m 的 取值范围是（ ） A． m =l B． m >l C． m ≥l D． m ≤l 【答案】C 21. （2011 上海，4，4 分）抛物线 y＝－(x＋2)2－3 的顶点坐标是（ ）． (A) （2，－3）； (B) （－2，3）； (C) （2，3）； (D) （－2，－3） ． 【答案】D 22. （2011 四川乐山 5，3 分）将抛物线 2y x  向左平移 2 个单位后，得到的抛物线的解析式是 A． 2( 2)y x   B． 2 2y x   C． 2( 2)y x   D． 2 2y x   【答案】A 23. （2011 四川凉山州，12，4 分）二次函数 2y ax bx c   的图像如图所示，反比列函数 ay x  与正 比列函数 y bx 在同一坐标系内的大致图像是（ ） 第 12 题 O x y O y x A O y x B O y x D O y x C 【答案】B 24. （2011 安徽芜湖，10,4 分）二次函数 2y ax bx c   的图象如图所示，则反比例函数 ay x  与一次函 数 y bx c  在同一坐标系中的大致图象是（ ）. 【答案】D 25. （2011 江苏无锡，9，3 分）下列二次函数中，图象以直线 x = 2 为对称轴，且经过点(0，1)的是 ( ) A．y = (x − 2)2 + 1 B．y = (x + 2)2 + 1 C．y = (x − 2)2 − 3 D．y = (x + 2)2 − 3 【答案】C 26. （2011 江苏无锡，10，3 分）如图，抛物线 y = x2 + 1 与双曲线 y = k x 的交点 A 的横坐标是 1，则关于 x 的不等式 k x + x2 + 1 < 0 的解集是 ( ) A．x > 1 B．x < −1 C．0 < x < 1 D．−1 < x < 0 （第 10 题） x y A 【答案】D 27. （2011 湖北黄冈，15，3 分）已知函数         2 2 1 1 3 5 1 3 x x y x x       ≤ ＞ ，则使 y=k 成立的 x 值恰好有三个，则 k 的值为（ ） A．0 B．1 C．2 D．3 【答案】D 28. （2011 广东肇庆，10，3 分）二次函数 522  xxy 有 A． 最大值 5 B． 最小值 5 C． 最大值 6 D． 最小值 6 【答案】D 29. （2011 湖北襄阳，12，3 分）已知函数 12)3( 2  xxky 的图象与 x 轴有交点，则 k 的取值范围是 A. 4k B. 4k C. 4k 且 3k D. 4k 且 3k 【答案】B 30. （2011 湖南永州，13，3 分）由二次函数 1)3(2 2  xy ，可知（ ） A．其图象的开口向下 B．其图象的对称轴为直线 3x C．其最小值为 1 D．当 3x 时，y 随 x 的增大而增大 【答案】C． 31. (20011 江苏镇江,8,2 分)已知二次函数 2 1 5y x x    ,当自变量 x 取 m 时,对应的函数值大于 0,当自变 量 x 分别取 m-1,m+1 时对应的函数值 1y 、 2y ,则必值 1y , 2y 满足 ( ) A. 1y >0, 2y >0 B. 1y <0, 2y <0 C. 1y <0, 2y >0 D. 1y >0, 2y <0 答案【B 】 32. （2011 安徽芜湖，10，4 分）二次函数 2y ax bx c   的图象如图所示，则反比例函数 ay x  与一次 函数 y bx c  在同一坐标系中的大致图象是（ ）. 【答案】D 33.（2010 湖北孝感，12，3 分）如图，二次函数 y=ax2+bx+c 的图象与 y 轴正半轴相交，其顶点坐标为 1 ,12      ， 下列结论：①ac＜0；②a+b=0；③4ac－b2=4a；④a+b+c＜0.其中正确的个数是（ ） A. 1 B. 2 C. 3 D. 4 【答案】C 34. （2011 湖南湘潭市，8，3 分）在同一坐标系中，一次函数 1 axy 与二次函数 axy  2 的图像可 能是 【答案】C 35. 二、填空题 1. （2011 浙江省舟山，15，4 分）如图，已知二次函数 cbxxy  2 的图象经过点（－1，0），（1，－2）， 当 y 随 x 的增大而增大时， x 的取值范围是 ． x y （第 15 题） O 1 1 （1,-2） cbxxy  2 -1 【答案】 1 2x  2. （2011 山东日照，17，4 分）如图，是二次函数 y＝ax2＋bx＋c（a≠0）的图象的一部分， 给出下列 命题 ：①a+b+c=0；②b＞2a；③ax2+bx+c=0 的两根分别为-3 和 1；④a-2b+c＞0．其中正确的命题 是 ．（只要求填写正确命题的序号） 【答案】①③． 3. （2011 浙江杭州，23， 10)设函数 2 (2 1) 1y kx k x    (k 为实数)． (1)写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这 两个特殊函数的图象； (2)根据所画图象，猜想出：对任意实数 K，函数的图象都具有的特征，并给予证明； (3)对任意负．实数 k，当 x0 时，y 随 x 的增大而减小.这个函数解析式为_________________________（写出一个即可） 【答案】如： 22 , 3, 5y y x y xx        等，写出一个即可. 10．（ 2011 重庆江津， 18，4 分）将抛物线 y=x2－2x 向上平移 3 个单位,再向右平移 4 个单位等到的抛物 线是_______. 【答案】y=(x-5)2+2 或 y=x2-10x+27 11. （2011 江苏淮安，14，3 分）抛物线 y=x2-2x-3 的顶点坐标是 . 【答案】（1，-4） 12. （2011 贵州贵阳，14，4 分）写出一个开口向下的二次函数的表达式______． 【答案】y=-x2+2x+1 13. （2011 广东茂名，15，3 分）给出下列命题： 命题 1．点(1，1)是双曲线 xy 1 与抛物线 2xy  的一个交点． 命题 2．点(1，2)是双曲线 xy 2 与抛物线 22xy  的一个交 点． 命题 3．点(1，3)是双曲线 xy 3 与抛物线 23xy  的一个交点． …… 请你观察上面的命题,猜想出命题 n ( n 是正整数): 【答案】点(1，n)是双曲线 x ny  与抛物线 2nxy  的一个交点 ． 14. （2011 山东枣庄，18，4 分）抛物线 2y ax bx c   上部分点的横坐标 x ，纵坐标 y 的对应值如下表： x … －2 －1 0 1 2 … y … 0 4 6 6 4 … 从上表可知，下列说法中正确的是 ．（填写序号） ①抛物线与 x 轴的一个交点为（3,0）； ②函数 2y ax bx c   的最大值为 6； ③抛物线的对称轴是 1 2x  ； ④在对称轴左侧， y 随 x 增大而增大． 【答案】①③④ 15. 三、解答题 1. （2011 广东东莞，15，6 分）已知抛物线 21 2y x x c   与 x 轴有交点． (1)求 c 的取值范围； (2)试确定直线 y＝cx+l 经过的象限，并说明理由． 【答案】（1）∵抛物线与 x 轴没有交点 ∴⊿＜0，即 1－2c＜0 解得 c＞ 1 2 (2)∵c＞ 1 2 ∴直线 y= 1 2 x＋1 随 x 的增大而增大， ∵b=1 ∴直线 y= 1 2 x＋1 经过第一、二、三象限 2. （ 2011 重庆江津， 25，10 分）已知双曲线 x ky  与抛物线 y=zx2+bx+c 交于 A(2,3)、B(m,2)、c(－3,n) 三点. (1)求双曲线与抛物线的解析式; (2)在平面直角坐标系中描出点 A、点 B、点 C,并求出△ABC 的面积, y x1 1 o 第 25 题图 -1 -1 ·A(2,3) y x1 1 o 第 25 题图 -1 -1 ·B(2,3) ·C(-2,-3) 【答案】(1)把点 A(2,3)代入 x ky  得 ：k=6· ∴反比例函数的解析式为： xy 6 · 把点 B(m,2)、C(－3,n)分别代入 xy 6 得： m=3,n=-2· 把 A(2,3)、B(3,2)、C(-3,-2)分别代入 y=ax2+bx+c 得：       239 239 324 cba cba cba 解之得            3 3 2 3 1 c b a ∴抛物线的解析式为：y=- 33 2 3 1 2  xx · (2)描点画图 S△ABC= 2 1 (1+6)×5- 2 1 ×1×1- 2 1 ×6×4= 122 1 2 35  =5· 3. （2011 江苏泰州，27，12 分）已知：二次函数 y=x2＋bx－3 的图像经过点 P（－2,5）． （1）求 b 的值，并写出当 1＜x≤3 时 y 的取值范围； （2）设点 P1（m,y1）、P2（m+1,y2）、P3(m+2,y3)在这个二次函数的图像上． ①当 m=4 时，y1、y2、y3 能否作为同一个三角形的三边的长？请说明理由； ②当 m 取不小于 5 的任意实数时，y1、y2、y3 一定能作为同一个三角形三边的长，请说明理由． 【答案】解：（1）把点 P 代入二次函数解析式得 5= （－2）2－2b－3，解得 b=－2. 当 1＜x≤3 时 y 的取值范围为－4＜y≤0. （2）①m=4 时，y1、y2、y3 的值分别为 5、12、21，由于 5+12＜21，不能成为三角形的三边长． ②当 m 取不小于 5 的任意实数时，y1、y2、y3 的值分别为 m2－2m－3、m2－4、m2＋2m－3，由于， m2 －2m－3＋m2－4＞m2＋2m－3，（m－2）2－8＞0， 当 m 不小于 5 时成立，即 y1＋y2＞y3 成立． 所以当 m 取不小于 5 的任意实数时，y1、y2、y3 一定能作为同一个三角形三边的长， 4. （2011 广东汕头，15，6 分）已知抛物线 21 2y x x c   与 x 轴有交点． (1)求 c 的取值范围； (2)试确定直线 y＝cx+l 经过的象限，并说明理由． 【答案】（1）∵抛物线与 x 轴没有交点 ∴⊿＜0，即 1－2c＜0 解得 c＞ 1 2 (2)∵c＞ 1 2 ∴直线 y= 1 2 x＋1 随 x 的增大而增大， ∵b=1 ∴直线 y= 1 2 x＋1 经过第一、二、三象限 5. （2011 湖南怀化，22，10 分）已知：关于 x 的方程 012)31(2  axaax （1） 当 a 取何值时，二次函数 12)31(2  axaaxy 的对称轴是 x=-2； （2） 求证：a 取任何实数时，方程 012)31(2  axaax 总有实数根. 【答案】 (1)解：∵二次函数 12)31(2  axaaxy 的对称轴是 x=-2 ∴ 22 )31(  a a 解得 a=-1 经检验 a=-1 是原分式方程的解. 所以 a=-1 时，二次函数 12)31(2  axaaxy 的对称轴是 x=-2； （2）1）当 a=0 时，原方程变为-x-1=0，方程的解为 x= -1； 2）当 a≠0 时，原方程为一元二次方程， 012)31(2  axaax ， 当 时，042  acb 方程总有实数根， ∴    0)12(4a31 2  aa 整理得， 0122  aa 0)1( 2 a ∵a≠0 时 0)1( 2 a 总成立 所以 a 取任何实数时，方程 012)31(2  axaax 总有实数根. 6. (2011 江苏南京，24，7 分)（7 分）已知函数 y=mx2－6x＋1（m 是常数）． ⑴求证：不论 m 为何值，该函数的图象都经过 y 轴上的一个定点； ⑵若该函数的图象与 x 轴只有一个交点，求 m 的值． 【答案】解：⑴当 x=0 时， 1y  ． 所以不论 m 为何值，函数 2 6 1y mx x   的图象经过 y 轴上的一个定点（0，1）． ⑵①当 0m  时，函数 6 1y x   的图象与 x 轴只有一个交点； ②当 0m  时，若函数 2 6 1y mx x   的图象与 x 轴只有一个交点，则方程 2 6 1 0mx x   有两 个相等的实数根，所以 2( 6) 4 0m   ， 9m  ． 综上，若函数 2 6 1y mx x   的图象与 x 轴只有一个交点，则 m 的值为 0 或 9． 10．（2011 四川绵阳 24，12）已知抛物线:y=x²-2x+m-1 与 x 轴只有一个交点，且与 y 轴交于 A 点, 如图，设它的顶点为 B (1)求 m 的值； (2)过 A 作 x 轴的平行线，交抛物线于点 C，求证是△ABC 是等腰直角三角形； (3)将此抛物线向下平移 4 个单位后，得到抛物线 C'，且与 x 轴的左半轴交于 E 点，与 y 轴交于 F 点，如图. 请在抛物线 C'上求点 P，使得△EFP 是以 EF 为直角边的直角三角形. 【答案】（1）抛物线与 x 轴只有一个交点，说明△=0，∴m=2 （2）∵抛物线的解析式是 y=x²-2x+1,∴A（0，1），B（1，0）∴△AOB 是等腰直角三角形，又 AC ∥OB,∴∠BAC=∠OAB=45°A，C 是对称点，∴AB=BC，∴△ABC 是等腰直角三角形。 （3）平移后解析式为 y=x²-2x-3,可知 E(-1,0),F(0,-3)∴EF 的解析式为：y=-3x-3,平面内互相垂直的两条直线的 k 值相乘=-1，所以过 E 点或 F 点的直线为 y=1 3x+b 把 E 点和 F 点分别代入可得 b=1 3 或-3，∴y=1 3x+1 3 或 y=1 3x-3 列方程得 y=1 3x+1 3 y=x²-2x-3 解方程 x1=-1,x2=10 3 , x1 是 E 点坐标舍去，把 x2=10 3 代入得 y=13 9 ,∴P1（10 3 ，13 9 ）同理 y=1 3x-3 y=x²-2x-3 易得 x1 = 0 舍去，x2= 7 3 代入 y=-20 9 ,∴P2(7 3,-20 9 ) 11. （2011 贵州贵阳，21，10 分） 如图所示，二次函数 y=-x2+2x+m 的图象与 x 轴的一个交点为 A（3，0），另一个交点为 B，且与 y 轴 交于点 C． （1）求 m 的值；（3 分） （2）求点 B 的坐标；（3 分） （3）该二次函数图象上有一点 D（x，y）（其中 x＞0，y＞0），使 S△ABD=S△ABC，求点 D 的坐标．（4 分） （第 21 题图） 【答案】解：（1）将（3，0）代入二次函数解析式，得 -32+2×3+m=0． 解得，m=3． （2）二次函数解析式为 y=-x2+2x+3，令 y=0，得 -x2+2x+3=0． 解得 x=3 或 x=-1． ∴点 B 的坐标为（-1，0）． （3）∵S△ABD=S△ABC，点 D 在第一象限， ∴点 C、D 关于二次函数对称轴对称． ∵由二次函数解析式可得其对称轴为 x=1，点 C 的坐标为（0，3）， ∴点 D 的坐标为（2，3）． 12. （2011 广东省，15，6 分）已知抛物线 21 2y x x c   与 x 轴有交点． (1)求 c 的取值范围； (2)试确定直线 y＝cx+l 经过的象限，并说明理由． 【答案】（1）∵抛物线与 x 轴没有交点 ∴⊿＜0，即 1－2c＜0 解得 c＞ 1 2 (2)∵c＞ 1 2 ∴直线 y= 1 2 x＋1 随 x 的增大而增大， ∵b=1 ∴直线 y= 1 2 x＋1 经过第一、二、三象限 13. （2011 广东肇庆，25，10 分）已知抛物线 22 4 3 mmxxy  （ m 0）与 x 轴交于 A 、 B 两点． （1）求证：抛物线的对称轴在 y 轴的左侧； （2）若 3 211  OAOB （O 是坐标原点），求抛物线的解析式； （3）设抛物线与 y 轴交于点C ，若 ABC 是直角三角形，求 ABC 的面积． 【答案】（1）证明：∵ m 0 ∴ 022  m a bx ∴抛物线的对称轴在 y 轴的左侧 （2）解：设抛物线与 x 轴交点坐标为 A（ 1x ，0），B（ 2x ，0）， 则 021  mxx ， 04 3 2 21  mxx ， ∴ 1x 与 2x 异号 又 3 211  OAOB 0 ∴ OBOA  由（1）知：抛物线的对称轴在 y 轴的左侧 ∴ 01 x ， 02 x ∴ 11 xxOA  , 2xOB  代入 3 211  OAOB 得： 3 21111 1212  xxxx 即 3 2 21 21   xx xx ，从而 3 2 4 3 2    m m ，解得： 2m ∴抛物线的解析式是 322  xxy （3）[解法一]：当 0x 时， 2 4 3 my  ∴抛物线与 y 轴交点坐标为C （0， 2 4 3 m ） ∵ ABC 是直角三角形，且只能有 AC⊥BC，又 OC⊥AB， ∴∠CAB＝ 90°— ∠ABC，∠BCO＝ 90°— ∠ABC，∴∠CAB ＝∠BCO ∴Rt△AOC∽Rt△COB， ∴ OC AO OB OC  ，即 OBOAOC 2 ∴ 21 2 2 4 3 xxm  即 24 4 3 16 9 mm  解得： 33 2m 此时 2 4 3 m ＝ 1)33 2(4 3 2  ，∴点C 的坐标为（0，—1）∴OC＝1 又 222 21 2 21 2 12 4)4 3(4)(4)()( mmmxxxxxx  ∵ m 0，∴ mxx 212  即 AB＝ m2 ∴ ABC 的面积＝ 2 1 ABOC＝ 2 1  m2 1＝ 33 2 [解法二]：略解: 当 0x 时， 2 4 3 my  ∴点C （0， 2 4 3 m ） ∵ ABC 是直角三角形 ∴ 222 BCACAB  ∴ 222 1 2 21 )4 3()( mxxx  222 2 )4 3( mx  ∴ 4 21 8 92 mxx  ∴ 42 8 9)4 3(2 mm  解得： 33 2m ∴ 33 2 4 322 1 4 3 2 1 2 1 22 21  mmmxxOCABS ABC 14. （2011 江苏盐城，23，10 分）已知二次函数 y= - 1 2 x2 -x+3 2 . （1）在给定的直角坐标系中，画出这个函数的图象； （2）根据图象，写出当 y ＜ 0 时，x 的取值范围； （3）若将此图象沿 x 轴向右平移 3 个单位，请写出平移后图象所对应的函数关系式． 【答案】（1）画图(如图)； （2）当 y ＜ 0 时，x 的取值范围是 x＜-3 或 x＞1； （3）平移后图象所对应的函数关系式为 y=- 1 2 （x-2）2+2（或写成 y=- 1 2x2+2x）.[来源:www.shulihua.net] 15. (20011 江苏镇江,24,7 分)如图,在△ABO 中,已知点 A( 3 ,3),B(-1,-1),O(0,0),正比例 y=-x 的图象是直线 l,直 线 AC∥x 轴交直线 l 于点 C. (1)C 点坐标为_____; (2)以点 O 为旋转中心,将△ABO 顺时针旋转角 a(0°0) 个单位，所得抛物线与 x 轴交与 C、D 两点，与原抛物线交与点 P. （1）求点 A 的坐标，并判断△PCA 存在时它的形状（不要求说理） （2）在 x 轴上是否存在两条相等的线段，若存在，请一一找出，并写出它们的长度（可用含 m 的式子 表示）；若不存在，请说明理由； （3）△CDP 的面积为 S，求 S 关于 m 的关系式。 x y DACO P y xO （第 10 题） 【关键词】二次函数、图形的平移、等腰三角形、面积等 【答案】解：（1）令-2x2+4x=0 得 x1=0，x2=2 ∴点 A 的坐标是（2，0）， △PCA 是等腰三角形， （2）存在。 OC=AD=m,OA=CD=2， （3）当 02 时，如图 2 作 PH⊥x 轴于 H，设 ( , )P PP x y , ∵A（2，0），C（m,0）, ∴AC=m-2，∴AH= 2 2 m  ∴ Px =OH= 2 2 mm  = 2 2 m  , 把把 Px = 2 2 m  代入 y=-2x2+4x，得 得, Py = 21 22 m  ∵CD=OA=2， ∴ 21 1 12( ) 22 2 2PS CD HP y m      g ． （2010 年广东省广州市）已知抛物线 y＝－x2＋2x＋2． （1）该抛物线的对称轴是 ，顶点坐标 ； （2）选取适当的数据填入下表，并在图 7 的直角坐标系内描点画出该抛物线的图象； x … … y … … （3）若该抛物线上两点 A（x1，y1），B（x2，y2）的横坐标满足 x1＞x2＞1，试比较 y1 与 y2 的大小． -5-4-3-2-1 O 1 2 3 4 5 x y -1 1 【关键词】抛物线的顶点、对称轴、描点法画图、函数增减性 【答案】解：（1）x＝1；（1，3） （2） x … －1 0 1 2 3 … y … －1 2 3 2 －1 … -5-4-3-2-1 O 1 2 3 4 5 x y -1 1 （3）因为在对称轴 x＝1 右侧，y 随 x 的增大而减小，又 x1＞x2＞1，所以 y1＜y2． （2010 年四川省眉山）如图，Rt△ABO 的两直角边 OA、OB 分别在 x 轴的负半轴和 y 轴的正半轴上，O 为 坐标原点，A、B 两点的坐标分别为（ 3 ，0）、（0，4），抛物线 22 3y x bx c   经过 B 点，且顶点在 直线 5 2x  上． （1）求抛物线对应的函数关系式； （2）若△DCE 是由△ABO 沿 x 轴向右平移得到的，当四边形 ABCD 是菱形时，试判断点 C 和点 D 是否 在该抛物线上，并说明理由； （3）若 M 点是 CD 所在直线下方该抛物线上的 一个动 点，过点 M 作 MN 平行于 y 轴交 CD 于点 N．设点 M 的横坐标为 t，MN 的长度为 l．求 l 与 t 之间的 函数关系式，并求 l 取最大值时，点 M 的 坐标． 【关键词】抛物线、菱形、最值 【答案】 解：（1）由题意，可设所求抛物 线对应 的函数关系式为 22 5( )3 2y x m   …（1 分） ∴ 22 54 ( )3 2 m    ∴ 1 6m   ……………………………………………………………（3 分） ∴所求函数关系式为： 2 22 5 1 2 10( ) 43 2 6 3 3y x x x      …………（4 分） （2）在 Rt△ABO 中，OA=3，OB=4， ∴ 2 2 5AB OA OB   ∵四边形 ABCD 是菱形 ∴BC=CD=DA=AB=5 ……………………………………（5 分） ∴C、D 两点的坐标分别是（5，4）、（2，0）． …………（6 分） 当 5x  时， 22 105 5 4 43 3y       当 2x  时， 22 102 2 4 03 3y       ∴点 C 和点 D 在所求抛物线上． …………………………（7 分） （3）设直线 CD 对应的函数关系式为 y kx b  ，则 5 4 2 0 k b k b      解得： 4 8,3 3k b   ． ∴ 4 8 3 3y x  ………（9 分） ∵MN∥y 轴，M 点的横坐标为 t， ∴N 点的横坐标也为 t． 则 22 10 43 3My t t   ， 4 8 3 3Ny t  ，……………………（10 分） ∴ 2 2 24 8 2 10 2 14 20 2 7 34 ( )3 3 3 3 3 3 3 3 2 2N Ml y y t t t t t t                  ∵ 2 03   ， ∴当 7 2t  时， 3 2l 最大 ， 此时点 M 的坐标为（ 7 2 ， 1 2 ）． ………………………………（12 分） 25．(2010 年重庆)今年我国多个省市遭受严重干旱．受旱灾的影响，4 月份，我市某蔬菜价格呈上升趋势， 其前四周每周的平均销售价格变化如下表： 周数 x 1 2 3 4 价格 y（元/千克） 2 2.2 2.4 2.6 进入 5 月，由于本地蔬菜的上市，此种蔬菜的平均销售价格 y（元/千克）从 5 月第 1 周的 2.8 元/千克下 降至第 2 周的 2.4 元/千克,且 y 与周数 x 的变化情况满足二次函数 cbxxy  2 20 1 ． （1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出 4 月份 y 与 x 所满足的函数关系式，并求出 5 月份 y 与 x 所满足的二次函数关系式； （2）若 4 月份此种蔬菜的进价 m（元/千克）与周数 x 所满足的函数关系为 2.14 1  xm ，5 月份的 进价 m（元/千克）与周数 x 所满足的函数关系为 25 1  xm ．试问 4 月份与 5 月份分别在哪一周销售 此种蔬菜一千克的利润最大？且最大利润分别是多少？ （3）若 5 月的第 2 周共销售 100 吨此种蔬菜．从 5 月的第 3 周起，由于受暴雨的影响，此种蔬菜的可 销售量将在第 2 周销量的基础上每周减少 %a ，政府为稳定蔬菜价格，从外地调运 2 吨此种蔬菜，刚好满 足本地市民的需要，且使此种蔬菜的销售价格比第２周仅上涨 %8.0 a ．若在这一举措下，此种蔬菜在第３ 周的总销售额与第 2 周刚好持平，请你参考以下数据，通过计算估算出 a 的整数值． （参考数据： 136937 2  ， 1444382  ， 1521392  ， 1600402  ， 1681412  ） 【答案】．解：（1）4 月份 y 与 x 满足的函数关系式为 8.12.0  xy . 把 8.2,1  yx 和 4.2,2  yx 分别代入 cbxxy  2 20 1 ，得        4.22420 1 ,8.220 1 cb cb 解得      .1.3 ,25.0 c b ∴五月份 y 与 x 满足的函数关系式为 .1.325.005.0 2  xxy （2）设 4 月份第 x 周销售此种蔬菜一千克的利润为 1W 元，5 月份第 x 周销售此种蔬菜一千克的利润为 2W 元. .6.005.0)2.14 1()8.12.0(1  xxxW ∵-0.05＜0，∴ 1W 随 x 的增大而减小. ∴当 1x 时， 1W 最大=-0.05+0.6=0.55. 2W =  )25 1()1.325.005.0( 2 xxx .1.105.005.0 2  xx ∵对称轴为 ,5.0)05.0(2 05.0  x 且-0.05＜0， ∴x＞-0.5 时，y 随 x 的增大而减小. ∴当 x=1 时， 2W 最大=1. 所以 4 月份销售此种蔬菜一千克的利润在第 1 周最大，最大利润为 0.55 元；5 月份销售此种蔬菜一千 克的利润在第 1 周最大，最大利润为 1 元. （3）由题意知：      .1004.2%8.014.22%1100  aa 整理，得 0250232  aa .解得 2 152923 a . ∵ 1521392  ， 1600402  ，而 1529 更接近 1521，∴ 391529  . ∴ 31a （舍去）或 8a . 答： a 的整数值为 8. 5．（2010 江苏泰州，5，3 分）下列函数中，y 随 x 增大而增大的是（ ） A. xy 3 B. 5 xy C. 1 2y x D. )0(2 1 2  xxy 【答案】C 【关键词】一次函数、反比例函数、二次函数的增减性 27．（2010 江苏泰州，27，12 分）如图，二次函数 cxy  2 2 1 的图象经过点 D      2 9,3 ，与 x 轴交于 A、B 两点． ⑴求 c 的值； ⑵如图①，设点 C 为该二次函数的图象在 x 轴上方的一点，直线 AC 将四边形 ABCD 的面积二等分，试 证明线段 BD 被直线 AC 平分，并求此时直线 AC 的函数解析式； ⑶设点 P、Q 为该二次函数的图象在 x 轴上方的两个动点，试猜想：是否存在这样的点 P、Q，使△AQP ≌△ABP？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用） 【答案】⑴ ∵抛物线经过点 D( 2 9,3 ) ∴ 2 9)3(2 1 2  c ∴c=6. ⑵过点 D、B 点分别作 AC 的垂线，垂足分别为 E、F，设 AC 与 BD 交点为 M， ∵AC 将四边形 ABCD 的面积二等分，即：S△ABC=S△ADC ∴DE=BF 又∵∠DME=∠BMF， ∠DEM=∠BFE ∴△DEM≌△BFM ∴DM=BM 即 AC 平分 BD ∵c=6. ∵抛物线为 62 1 2  xy ∴A（ 0,32 ）、B（ 0,32 ） ∵M 是 BD 的中点 ∴M（ 4 9,2 3 ） 设 AC 的解析式为 y=kx+b，经过 A、M 点       4 9 2 3 032 bk bk 解得         5 9 10 33 b k  直线 AC 的解析式为 5 9 10 33  xy . ⑶存在．设抛物线顶点为 N(0，6)，在 Rt △ AQN 中，易得 AN= 4 3 ，于是以 A 点为圆心，AB= 4 3 为半 径作圆与抛物线在 x 上方一定有交点 Q，连接 AQ，再作∠QAB 平分线 AP 交抛物线于 P，连接 BP、PQ，此 时由“边角边”易得 △ AQP≌△ABP． 【关键词】二次函数、一次函数、解直角三角形及其知识的综合运用 (201 0 年 浙 江 省 绍 兴 市 )如图,设抛物线 C1:   51 2  xay , C2:   51 2  xay ,C1 与 C2 的交点为 A, B,点 A 的坐标是 )4,2( ,点 B 的横坐标是－2. （1）求 a 的值及点 B 的坐标； （2）点D在线段AB上,过D作x轴的垂线,垂足为点H, 在DH的右侧作正三角形DHG. 记过C2顶点Ｍ的 直线为 l ,且 l 与x轴交于点N. ① 若l 过△DHG 的顶点 G,点 D 的坐标为 (1, 2)，求点 N 的横坐标； ② 若l 与△DHG的边DG相交,求点N的横 坐标的取值范围. 【答案】解：（1）∵ 点 A )4,2( 在抛物线 C1 上，∴ 把点 A 坐标代入   51 2  xay 得 a =1. ∴ 抛物线 C1 的解析式为 422  xxy , 设 B(－2,b)， ∴ b＝－4, ∴ B(－2,－4) . （2）①如图 1， ∵ M(1, 5)，D(1, 2), 且 DH⊥x 轴，∴ 点 M 在 DH 上，MH=5. 过点 G 作 GE⊥DH,垂足为 E, 由△DHG 是正三角形,可得 EG= 3 , EH=1， ∴ ME＝4. 设 N ( x, 0 ), 则 NH＝x－1, 由△MEG∽△MHN,得 HN EG MH ME  , ∴ 1 3 5 4  x , ∴ x 134 5  , ∴ 点 N 的横坐标为 134 5  ． ② 当点Ｄ移到与点 A 重合时,如图 2， 直线 l 与 DG 交于点 G,此时点Ｎ的横坐标最大． 过点Ｇ,Ｍ作 x 轴的垂线,垂足分别为点Ｑ,F, 设Ｎ（x，0）， ∵ A (2, 4), ∴ G ( 322  , 2), ∴ NQ= 322 x ，ＮF = 1x , GQ=2, MF =5. ∵ △NGQ∽△NMF， ∴ MF GQ NF NQ  , ∴ 5 2 1 322   x x , ∴ 3 8310 x . 当点 D 移到与点 B 重合时,如图 3， 直线 l 与 DG 交于点 D,即点 B, 此时点 N 的横坐标最小. ∵ B(－2, －4), ∴ H(－2, 0), D(－2, －4), 设 N（x，0）， ∵ △BHN∽△MFN， ∴ MF BH FN NH  ， ∴ 5 4 1 2   x x , ∴ 3 2x . 第 24 题图 第 24 题图 1 第 24 题图 2 第 24 题图 3 图 4 ∴ 点 N 横坐标的范围为 3 2 ≤x≤ 3 8310  . （2010 年宁德市）（本题满分 12 分）如图 1，抛物线 34 1 4 1 2  xxy 与 x 轴交于 A、C 两点，与 y 轴 交于 B 点，与直线 bkxy  交于 A、D 两点。 ⑴直接写出 A、C 两点坐标和直线 AD 的解析式； ⑵如图 2，质地均匀的正四面体骰子的各个面上依次标有数字－1、1、3、4.随机抛掷这枚骰子两次， 把第一次着地一面的数字 m 记做 P 点的横坐标，第二次着地一面的数字 n 记做 P 点的纵坐标.则点  nmP , 落在图 1 中抛物线与直线围成区域内（图中阴影部分，含边界）的概率是多少？ 【答案】解：⑴ A 点坐标：(－3，0)，C 点坐标：C(4，0)； 直线 AD 解析式： 4 3 4 1  xy . ⑵ 所有可能出现的结果如下（用列树状图列举所有可能同样得分）： 第一次 第二次 －1 1 3 4 －1 （－1，－ 1） （－1， 1） （－1，3）（－1，4） 1 （1，－1）（1， 1） （1，3） （1，4） 3 （3，－1）（3， 1）（3， 3）（3， 4） 4 （4，－1）（4， 1）（4， 3）（4， 4） 总共有 16 种结果，每种结果出现的可能性相同，而落在图 1 中抛物线与直线围成区域内的结果有 7 种： （－1，1），（1，－1），（1，1），（1，3），（3，－1），（3，1），（4，－1）. y x0 D(5,-2) C B A 图 1 图 2 -1 3 因此 P（落在抛物线与直线围成区域内）＝ 16 7 . （注：落在抛物线与直线围成区域内的点列举错误 1 个扣 1 分，2 个及 2 个以上扣 2 分。由点列举错误 引起概率计算错误不扣分。） （2010 年宁德市）（本题满分 13 分）如图，在梯形 ABCD 中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB ＝30°.点 E、F 同时从 B 点出发，沿射线 BC 向右匀速移动.已知 F 点移动速度是 E 点移动速度的 2 倍， 以 EF 为一边在 CB 的上方作等边△EFG．设 E 点移动距离为 x（x＞0）. ⑴△EFG 的边长是____（用含有 x 的代数式表示），当 x＝2 时，点 G 的位置在_______； ⑵若△EFG 与梯形 ABCD 重叠部分面积是 y，求 ①当 0＜x≤2 时，y 与 x 之间的函数关系式； ②当 2＜x≤6 时，y 与 x 之间的函数关系式； ⑶探求⑵中得到的函数 y 在 x 取含何值时，存在最大值，并求出最大值. 【答案】解：⑴ x，D 点； ⑵ ①当 0＜x≤2 时，△EFG 在梯形 ABCD 内部，所以 y＝ 4 3 x2； ②分两种情况： Ⅰ.当 2＜x＜3 时，如图 1，点 E、点 F 在线段 BC 上， △EFG 与梯形 ABCD 重叠部分为四边形 EFNM， ∵∠FNC＝∠FCN＝30°,∴FN＝FC＝6－2x.∴GN＝3x－6. 由于在 Rt△NMG 中，∠G＝60°， 所以，此时 y＝ 4 3 x2－ 8 3 （3x－6）2＝ 2 39 2 39 8 37 2  xx . Ⅱ.当 3≤x≤6 时，如图 2，点 E 在线段 BC 上，点 F 在射线 CH 上， △EFG 与梯形 ABCD 重叠部分为△ECP， ∵EC＝6－x, ∴y＝ 8 3 （6－x）2＝ 2 39 2 33 8 3 2  xx . ⑶当 0＜x≤2 时，∵y＝ 4 3 x2 在 x＞0 时，y 随 x 增大而增大， ∴x＝2 时，y 最大＝ 3 ； B E→ F→ C A D G y O B C D 1 M x 2 4 A 当 2＜x＜3 时，∵y＝ 2 39 2 39 8 37 2  xx 在 x＝ 7 18 时，y 最大＝ 7 39 ； 当 3≤x≤6 时，∵y＝ 2 39 2 33 8 3 2  xx 在 x＜6 时，y 随 x 增大而减小， ∴x＝3 时，y 最大＝ 8 39 . 综上所述：当 x＝ 7 18 时，y 最大＝ 7 39 . 21（8 分）（2010 年浙江省东阳市）如图，足球场上守门员在 O 处开出一高球，球从离地面 1 米的 A 处飞 出（ A 在 y 轴上），运动员乙在距O 点 6 米的 B 处发现球在自己头的正上方达到最高点 M ，距地面约 4 米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同， 最大高度减少到原来最大高度的一半． （1）求足球开始飞出到第一次落地时，该 抛物线的表达式． （2）足球第一次落地点C 距守门员多少 米？（取 734  ） （3）运动员乙要抢到第二个落点 D ，他应 再向前跑多少米？（取 562  ） 【关键词】二次函数 【答案】（1）y=－ 4)6(12 1 2 x （3 分） （2）y=0, x=6+4 3 ︽13………………………………………………………………2 分 （3）设 y= 2)(12 1 2  mx m=13+2 6 ︽18 y=0, x=18±2 6 ︽23 ∴ 再向前跑 10 米…………………3 分 23（10 分）（2010 年浙江省东阳市）如图，在一块正方形 ABCD 木板上要贴三种不同的墙纸，正方形 EFCG 部分贴 A 型墙纸，△ABE 部分贴 B 型墙纸，其余部分贴 C 型墙纸。A 型、B 型、C 型三种墙纸的单价分别为 B E F C A D G N M 图 1 B E C F A D G P H 图 2 每平方 60 元、80 元、40 元。 探究 1：如果木板边长为 2 米，FC＝1 米，则一块木板用墙纸的费用需 ▲ 元； 探究 2：如果木板边长为 1 米，求一块木板需用墙纸的最省费用； 探究 3：设木板的边长为 a（a 为整数），当正方形 EFCG 的边长为多少时？墙纸费用最省；如要用这 样的多块木板贴一堵墙（7×3 平方米）进行装饰， 要求每块木板 A 型的墙纸不超过 1 平方米，且尽量 不浪费材料，则需要这样的木板 ▲ 块。 【关键词】二次函数 最值 【答案】（1）220………………………………………………………………… 2 分 （2）y=20x2—20x+60 ……………………………………………………………………2 分 当 x= 2 1 时，y 小=55 元。…………………………………………………………………1 分 （3）y=20x2—20ax+60a2 …………………………………………………………………2 分 当 x= 2 1 a 时，…………………………………………………………………………1 分 21 块 …………………………………………………………………………………2 分 1.（2010 年四川省眉山市）如图，Rt△ABO 的两直角边 OA、OB 分别在 x 轴的负半轴和 y 轴的正半轴上，O 为坐标原点，A、B 两点的坐标分别为（ 3 ，0）、（0，4），抛物线 22 3y x bx c   经过 B 点，且顶点 在直线 5 2x  上． （1）求抛物线对应的函数关系式； （2）若△DCE 是由△ABO 沿 x 轴向右平移得到的，当四边形 ABCD 是菱形时，试判断点 C 和点 D 是否 在该抛物线上，并说明理由； （3）若 M 点是 CD 所在直线下方该抛物线上的一个动点，过点 M 作 MN 平行于 y 轴交 CD 于点 N．设 点 M 的横坐标为 t，MN 的长度为 l．求 l 与 t 之间的函数关系式，并求 l 取最大值时，点 M 的坐 标． 【关键词】抛物线、直线的关系式、菱形的性质 【 答 案 】 解 ：（ 1 ） 由 题 意 ， 可 设 所 求 抛 物 线 对 应 的 函 数 关 系 式 为 22 5( )3 2y x m   ∴ 22 54 ( )3 2 m    ∴ 1 6m   ∴所求函数关系式为： 2 22 5 1 2 10( ) 43 2 6 3 3y x x x      （2）在 Rt△ABO 中，OA=3，OB=4， ∴ 2 2 5AB OA OB   ∵四边形 ABCD 是菱形 ∴BC=CD=DA=AB=5 ∴C、D 两点的坐标分别是（5，4）、（2，0）． 当 5x  时， 22 105 5 4 43 3y       当 2x  时， 22 102 2 4 03 3y       ∴点 C 和点 D 在所求抛物线上． （3）设直线 CD 对应的函数关系式为 y kx b  ，则 5 4 2 0 k b k b      解得： 4 8,3 3k b   ． ∴ 4 8 3 3y x  ∵MN∥y 轴，M 点的横坐标为 t， ∴N 点的横坐标也为 t． 则 22 10 43 3My t t   ， 4 8 3 3Ny t  ， ∴ 2 2 24 8 2 10 2 14 20 2 7 34 ( )3 3 3 3 3 3 3 3 2 2N Ml y y t t t t t t                  ∵ 2 03   ， ∴当 7 2t  时， 3 2l 最大 ， 此时点 M 的坐标为（ 7 2 ， 1 2 ）． 26. (2010 重庆市潼南县)如图, 已知抛物线 cbxxy  2 2 1 与 y 轴相交于 C，与 x 轴相交于 A、B，点 A 的坐标为（2，0），点 C 的坐标为（0，-1）. （1）求抛物线的解析式； （2）点 E 是线段 AC 上一动点，过点 E 作 DE⊥x 轴于点 D，连结 DC，当△DCE 的面积最大时，求点 D 的坐标； （3）在直线 BC 上是否存在一点 P，使△ACP 为等腰三角形，若存在，求点 P 的坐标，若不存在，说 明理由. 解：（1）∵二次函数 cbxxy  2 2 1 的图像经过点 A（2，0）C(0,－1) ∴      1 022 c cb 解得： b=－ 2 1 c=－1-------------------2 分 ∴二次函数的解析式为 12 1 2 1 2  xxy --------3 分 （2）设点 D 的坐标为（m，0） （0＜m＜2） ∴ OD=m ∴AD=2-m 由△ADE∽△AOC 得， OC DE AO AD  --------------4 分 ∴ 12 2 DEm  ∴DE= 2 2 m -----------------------------------5 分 ∴△CDE 的面积= 2 1 × 2 2 m ×m AB C E D x y o 题图26 = 24 2 mm  = 4 1)1(4 1 2  m 当 m=1 时，△CDE 的面积最大 ∴点 D 的坐标为（1，0）--------------------------8 分 （3）存在 由(1)知：二次函数的解析式为 12 1 2 1 2  xxy 设 y=0 则 12 1 2 10 2  xx 解得：x1=2 x2=－1 ∴点 B 的坐标为（－1，0） C（0，－1） 设直线 BC 的解析式为：y=kx＋b ∴      1 0 b bk 解得：k=-1 b=-1 ∴直线 BC 的解析式为: y=－x－1 在 Rt△AOC 中，∠AOC=900 OA=2 OC=1 由勾股定理得：AC= 5 ∵点 B(－1,0) 点 C（0，－1） ∴OB=OC ∠BCO=450 ①当以点 C 为顶点且 PC=AC= 5 时， 设 P(k, －k－1) 过点 P 作 PH⊥y 轴于 H ∴∠HCP=∠BCO=450 CH=PH=∣k∣ 在 Rt△PCH 中 k2+k2=  2 5 解得 k1= 2 10 ， k2=－ 2 10 ∴P1（ 2 10 ，－ 12 10  ） P2（－ 2 10 ， 12 10  ）---10 分 ②以 A 为顶点，即 AC=AP= 5 设 P(k, －k－1) 过点 P 作 PG⊥x 轴于 G AG=∣2－k∣ GP=∣－k－1∣ 在 Rt△APG 中 AG2＋PG2=AP2 （2－k)2+(－k－1)2=5 解得：k1=1,k2=0(舍) ∴P3(1, －2) ----------------------------------11 分 ③以 P 为顶点，PC=AP 设 P(k, －k－1) 过点 P 作 PQ⊥y 轴于点 Q PL⊥x 轴于点 L ∴L(k,0) ∴△QPC 为等腰直角三角形 PQ=CQ=k 由勾股定理知 CP=PA= 2 k ∴AL=∣k-2∣, PL=｜－k－1｜ 在 Rt△PLA 中 ( 2 k)2=(k－2)2＋(k＋1)2 解得：k= 2 5 ∴P4( 2 5 ,－ 2 7 ) ------------------------12 分 综上所述： 存在四个点：P1（ 2 10 ，－ 12 10  ） P2（- 2 10 ， 12 10  ） P3(1, －2) P4( 2 5 ,－ 2 7 ) （2010 年日照市）如图，小明在一次高尔夫球争霸赛中，从山坡下 O 点打出一球向球洞 A 点飞去，球的 飞行路线为抛物线，如果不考虑空气阻力，当球达到最大水平高度 12 米时，球移动的水平距离为 9 米 ．已 知山坡 OA 与水平方向 OC 的夹角为 30o，O、A 两点相距 8 3 米． （1）求出点 A 的坐标及直线 OA 的解析式； （2）求出球的飞行路线所在抛物线的解析式； （3）判断小明这一杆能否把高尔夫球从 O 点直接打 入 球 洞 A 点 ． （本题满分 10 分） 解：（1）在 Rt△AOC 中， ∵∠AOC=30 o ，OA=8 3 ， ∴AC=OA·sin30o=8 3 × 2 1 = 34 ， OC=OA·cos30o=8 3 × 2 3 =12． ∴点 A 的坐标为（12， 34 ）． …………………………………2 分 设 OA 的解析式为 y=kx，把点 A（12， 34 ）的坐标代入得： 34 =12k ， ∴k= 3 3 ， ∴OA 的解析式为 y= 3 3 x； …………………… ……………………4 分 (2) ∵顶点 B 的坐标是（9，12）, 点 O 的坐标是（0，0） ∴设抛物线的解析式为 y=a(x-9) 2 +12，…………………………………6 分[来源:www.shulihua.net] 把点 O 的坐标代入得： 0=a（0-9） 2 +12，解得 a= 27 4 ， ∴抛物线的解析式为 y= 27 4 (x-9) 2 +12 及 y= 27 4 x 2 + 3 8 x； …………………………………………………8 分 (3) ∵当 x=12 时，y= 3 32  34 ， ∴小明这一杆不能把高尔夫球从 O 点直接打入球洞 A 点． （2010 年日照市）如图，是二次函数 y=ax2+bx+c 图象的一部分，其对称轴为直线 x=1，若其与 x 轴一交点 为 A（3，0），则由图象可知，不等式 ax2+bx+c＜0 的解集是 . 答案：－1＜x＜3 ; 25．（2010 年湖北黄冈市）（15 分）已知 抛 物 线 2 ( 0)y ax bx c a    顶点为 C（1，1）且过原点 O.过抛物线上一点 P（x，y）向直线 5 4y  作垂线，垂足为 M，连 FM（如图）. （1）求字母 a，b，c 的值； （2）在直线 x＝1 上有一点 3(1, )4F ，求以 PM 为底边的等腰三角形 PFM 的 P 点的坐标，并证明此时△ PFM 为正三角形； （3）对抛物线上任意一点 P，是否总存在一点 N（1，t），使 PM＝PN 恒成立，若存在请求出 t 值，若不 存在请说明理由. （1）a＝－1，b＝2，c＝0 （2）过 P 作直线 x=1 的垂线，可求 P 的纵坐标为 1 4 ，横坐标为 11 32  .此时，MP＝MF＝PF＝1，故 △MPF 为正三角形. （3）不存在.因为当 t＜ 5 4 ，x＜1 时，PM 与 PN 不可能相等，同理，当 t＞ 5 4 ，x＞1 时，PM 与 PN 不 可能相等. （2010 年湖北黄冈市）（11 分）某同学从家里出发，骑自行车上学时，速度 v（米/秒）与时间 t（秒）的 关系如图 a，A（10，5），B（130，5），C（135，0）. （1）求该同学骑自行车上学途中的速度 v 与时间 t 的函数关系式； （2）计算该同学从家到学校的路程（提示：在 OA 和 BC 段的运动过程中的平均速度分别等于它们中 点时刻的速度，路程＝平均速度×时间）； （3）如图 b，直线 x＝t（0≤t≤135），与图 a 的图象相交于 P、Q，用字母 S 表示图中阴影部分面积， 试求 S 与 t 的函数关系式； （4）由（2）（3），直接猜出在 t 时刻，该同学离开家所超过的路程与此时 S 的数量关系. 图 a 图 b （1） 1 (0 10)2 5 (10 130) 135 (130 135) v t t v t v t t               　　 　　 　　 （2）2.5×10+5×120+2×5＝635（米） （3） 2 2 1 (0 10)4 5 25 (10 130) 1 (130 135)2 S t t S t t S t t                 　　 　　 +135t-8475　　 (4) 相等的关系 （2010 年湖北黄冈市）若函数 2 2 ( 2) 2 x xy x     　　≤ 　（x>2） ，则当函数值 y＝8 时，自变量 x 的值是（ ） A．± 6 B．4 C．± 6 或 4 D．4 或－ 6 14.D 7. （2010 年安徽中考） 若二次函数 52  bxxy 配方后为 kxy  2)2( 则 b 、 k 的值分别 为………………（ ） A）0.5 B）0.1 C）—4.5 D）—4.1 【关键词】二次函数 【答案】D 23．（2010 年浙江省东阳市）（10 分）如图，在一块正方形 ABCD 木板上要贴三种不同的墙纸，正方形 EFCG 部分贴 A 型墙纸，△ABE 部分贴 B 型墙纸，其余部分贴 C 型墙纸。A 型、B 型、C 型三种墙纸的单价分别为 每平方 60 元、80 元、40 元。 探究 1：如果木板边长为 2 米，FC＝1 米，则一块木板用墙纸的费用需 ▲ 元； 探究 2：如果木板边长为 1 米，求一块木板需用墙纸的最省费用； 探究 3：设木板的边长为 a（a 为整数），当正方形 EFCG 的边长为多少时？墙纸费用最省；如要用这 样的多块木板贴一堵墙（7×3 平方米）进行装饰， 要求每块木板 A 型的墙纸不超过 1 平方米，且尽量 不浪费材料，则需要这样的木板 ▲ 块。 【关键词】二次函数、正方形 【答案】 220)1.(23 ………………………………………………………………… 2 分 （2）y=20x2—20x+60 ……………………………………………………………………2 分 当 x= 2 1 时，y 小=55 元。…………………………………………………………………1 分 （3）y=20x2—20ax+60a2 …………………………………………………………………2 分 当 x= 2 1 a 时，…………………………………………………………………………1 分 21 块 …………………………………………………………………………………2 分 22. （2010 年安徽中考）春节期间某水库养殖场为适应市场需求，连续用 20 天时间，采用每天降低水位 以减少捕捞成本的办法，对水库中某种鲜鱼进行捕捞、销售。 九（1）班数学建模兴趣小组根据调查，整理出第 x 天（ 201  x 且 x 为整数）的捕捞与销售的相关 信息如下： ⑴在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的？ ⑵假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出，求第 x 天的收入 y（元）与 x （天）之间的函数关系式？（当天收入＝日销售额—日捕捞成本） 试说明⑵中的函数 y 随 x 的变化情况，并指出在第几天 y 取得最大值，最大值是多少？ 【关键词】二次函数 【答案】 解：（1）解：该养殖场每天的捕捞量与前一天的捕捞量相比每天减少了 10kg. （1） 解：由题意，得 220(950 10 ) (5 )(950 10 ) 2 40 142505 xy x x x x         （3）解：∵ 2 22 0, 2 40 14250 2( 10) 14450y x x x          又1 20x  且 x 为整数， ∴当1 10x  时，y 随 x 的增大而增大 当10 20x  时，y 随 x 的增大而减小 当 x=10 时，即在第 10 天，y 取得最大值，最大值为 14450 元。 1、（2010 年宁波市）如图，已知二次函数 cbxxy  2 2 1 的图象经过 A（2，0）、B（0，－6）两点。 （1）求这个二次函数的解析式 （2）设该二次函数的对称轴与 x 轴交于点 C，连结 BA、BC，求△ABC 的面积。 [来源:www.shulihua.net] 【关键词】二次函数 【答案】解：（1）把 A（2，0）、B（0，－6）代入 cbxxy  2 2 1 得：      6 022 c cb 解得      6 4 c b ∴这个二次函数的解析式为 642 1 2  xxy y xC A O B 第 20 题 （2）∵该抛物线对称轴为直线 4 )2 1(2 4   x ∴点 C 的坐标为（4，0） ∴ 224  OAOCAC ∴ 6622 1 2 1  OBACS ABC 2. (2010 年兰州市)二次函数 23 6 5y x x    的图像的顶点坐标是 A．（-1，8） B．（1，8） C．（-1，2） D．（1，-4） 【关键词】二次函数 【答案】A 3. (2010 年兰州市)抛物线 cbxxy  2 图像向右平移 2 个单位再向下平移 3 个单位，所得图像的解析 式为 322  xxy ，则 b、c 的值为 A . b=2， c=2 B. b=2，c=0 C . b= -2，c=-1 D. b= -3， c=2 【关键词】二次函数 【答案】B 4. (2010 年兰州市)如图，小明的父亲在相距 2 米的两棵树 间拴了一根绳子，给小明做了一个简易的秋千.拴绳子 的地方距地面高都是2.5米，绳子自然下垂呈抛物线状， 身高 1 米的小明距较近的那棵树 0.5 米时，头部刚好接 触到绳子，则绳子的最低点距地面的距离为 米. 【关键词】二次函数 【答案】 2 1 3. (2010 年兰州市)（本题满分 11 分）如图 1，已知矩形 ABCD 的顶点 A 与点 O 重合，AD、AB 分别在 x 轴、 y 轴上，且 AD=2，AB=3；抛物线 cbxxy  2 经过坐标原点 O 和 x 轴上另一点 E（4,0） （1）当 x 取何值时，该抛物线的最大值是多少？ （2）将矩形 ABCD 以每秒1 个单位长度的速度从图 1 所示的位置沿 x 轴的正方向匀速平行移动，同时一 动点 P 也以相同的速度从点 A 出发向 B 匀速移动.设它们运动的时间为 t 秒（0≤t≤3），直线 AB 与 该 抛物线的交点为 N（如图 2 所示）. ① 当 4 11t 时，判断点 P 是否在直线 ME 上，并说明理由； ② 以 P、N、C、D 为顶点的多边形面积是否可能为 5，若有可能，求出此时 N 点的坐标；若无可 能，请说明理由． 图 1 第 28 题图 图 2 【关键词】二次函数 【答案】 解：（1）因抛物线 cbxxy  2 经过坐标原点 O（0,0）和点 E（4,0） 故可得 c=0,b=4 所以抛物线的解析式为 xxy 42  …………………………………………1 分 由 xxy 42   22 4y x   得当 x=2 时，该抛物线的最大值是 4. …………………………………………2 分 （2）① 点 P 不在直线 ME 上. 已知 M 点的坐标为(2,4)，E 点的坐标为(4,0)， 设直线 ME 的关系式为 y=kx+b. 于是得      42 04 bk bk ，解得      8 2 b k 所以直线 ME 的关系式为 y=-2x+8. …………………………………………3 分 由已知条件易得，当 4 11t 时，OA=AP= 4 11 ， )4 11,4 11(P …………………4 分 ∵ P 点的坐标不满足直线 ME 的关系式 y=-2x+8. [来源:www.shulihua.net] ∴ 当 4 11t 时，点 P 不在直线 ME 上. ……………………………………5 分 ②以 P、N、C、D 为顶点的多边形面积可能为 5 ∵ 点 A 在 x 轴的非负半轴上，且 N 在抛物线上， ∴ OA=AP=t. ∴ 点 P，N 的坐标分别为(t,t)、(t,-t 2+4t) …………………………………6 分 ∴ AN=-t 2+4t (0≤t≤3) , ∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t )≥0 , ∴ PN=-t 2+3 t …………………………………………………………………………………7 分 （ⅰ）当 PN=0，即 t=0 或 t=3 时，以点P，N，C，D 为顶点的多边形是三角形，此三角形的高为 AD，∴ S= 2 1 DC·AD= 2 1 ×3×2=3. （ⅱ）当 PN≠0 时，以点 P，N，C，D 为顶点的多边形是四边形 ∵ PN∥CD，AD⊥CD， ∴ S= 2 1 (CD+PN)·AD= 2 1 [3+(-t 2+3 t)]×2=-t 2+3 t+3…………………8 分 当-t 2+3 t+3=5 时，解得 t=1、2…………………………………………………9 分 而 1、2 都在 0≤t≤3 范围内，故以 P、N、C、D 为顶点的多边形面积为 5 综上所述，当 t=1、2 时，以点 P，N，C，D 为顶点的多边形面积为 5， 当 t=1 时，此时 N 点的坐标（1,3）………………………………………10 分 F E G(O) B A C  H K F E G(O) B A C 图① 图② 当 t=2 时，此时 N 点的坐标（2,4）………………………………………11 分 说明：（ⅱ）中的关系式，当 t=0 和 t=3 时也适合.（故在阅卷时没有（ⅰ），只有 1.(2010 福建泉州市惠安县)如图，抛物线 322  xxy 与 x 轴交于 A B， 两点，与 y 轴交于 C 点． （1）求抛物线的顶点坐标； (2) 设直线 3y x   与 y 轴的交点是 D ，在线段 BD 上任取一点 E （不与 B D， 重合），经过 A B E， ， 三点的圆交直线 BC 于点 F ，试判断 AEF△ 的形状，并说明理由. 【关键词】二次函数 【答案】解：（1） 322  xxy = 31122  xx = 4)1( 2 x ∴ （1，-4）； （2）由抛物线 322  xxy 和直线 3y x   可求得： A（-1，0）、B（3，0）、C（0，-3）、D（0，3） ∴OB=OC=OD=3 ∴∠OBD=∠OBC=450 又∵∠OBD=∠AFE，∠OBC=∠AEF ∴∠AFE=∠AEF=450 ∴∠EAF=900，AE=AF ∴△AEF 是等腰直角三角形 2.(2010 福建泉州市惠安县) 如图，把两个全等的等腰直角三角板 ABC 和 EFG（其直角边长均为 4）叠放在 一起，使三角板 EFG 的直角顶点 G 与三角板 ABC 的斜边中点 O 重合（如图①）.现将三角板 EFG 绕 O 点 按顺时针方向旋转（旋转角α满足条件：00＜α＜900），四边形 CHGK 是旋转过程中两三角板的重叠部 分（如图②）. （1）在上述过程中，BH 与 CK 有怎样的数量关系？证明你发现的结论； (2)连接 HK，在上述旋转过程中，设 BH=x，△GKH 的面积为 y, ①求 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围； ②当△GKH 的面积恰好等于△ABC 面积的 5 16 ，求此时 BH 的长. x y O x＝1 第 25 题 A C B 【关键词】二次函数 【答案】（1）BH=CK. 如图 2，∵点 O 是等腰直角三角板 ABC 斜边中点 ∴∠B=∠GCK=450 ，BG=CG 由旋转的性质，知∠BGH=∠CGK ∴△BGH≌△CGK ∴BH=CK. （2）① 由(1)易知 S 四边形 CHGK = S2 1 △ABC =4， ∴S△GKH = S 四边形 CHGK-S△KCH=4- 2 1 CH×CK 得 y = 422 1 2  xx （0＜χ＜4） ②当 y = 5 16 ×8= 2 5 时， 即 422 1 2  xx = 2 5 ，解得χ=1 或χ=3. ∴当△GKH 的面积恰好等于△ABC 面积的 5 16 时，BH=1 或 BH=3. 3.(2010 年山东聊城)如图，已知抛物线 y＝ax2＋bx＋c(a≠0)的对称轴为 x＝1，且抛物线经过 A（—1，0）、 B（0，—3）两点，与 x 轴交于另一点 B． （1）求这条抛物线所对应的函数关系式； （2）在抛物线的对称轴 x＝1 上求一点 M，使点 M 到点 A 的距离与到点 C 的距离之和最小，并求出此 时点 M 的坐标； （3）设点 P 为抛物线的对称轴 x＝1 上的一动点，求使∠PCB＝90°的点 P 的坐标． 【关键词】二次函数 【答案】⑴设抛物线的解析式为 y ＝ax2＋bx＋c，则有：          12 3 0 a b c cba 解得：       3 2 1 c b a ，所以抛物线的解析式为 y ＝x2－2x－3. ⑵令 x2－2x－3＝0，解得 x1＝－１，x2＝3,所以 B 点坐标为（3，0）. 设直线 BC 的解析式为 y ＝kx2＋b, 则    3 03 b bk ，解得    3 1 b k ，所以直线解析式是 y ＝x－3. 当 x＝1 时，y＝－2.所以 M 点的坐标为（1，－2）. ⑶方法一：要使∠PBC＝90°，则直线 PC 过点 C，且与 BC 垂直， 又直线 BC 的解析式为 y ＝x－3， 所以直线 PC 的解析式为 y ＝－x－3，当 x＝1 时，y＝－4， 所以 P 点坐标为（1，－4）. 方法二：设 P 点坐标为（1，y），则 PC2＝12＋（－3－y）2,BC2＝32＋32；PB2＝22＋y2 由∠PBC＝90°可知△PBC 是直角三角形，且 PB 为斜边，则有 PC2＋BC2＝PB2. 所以：[12＋（－3－y）2]＋[32＋32]＝22＋y2；解得 y ＝－4， 所以 P 点坐标为（1，－4）. 1、（2010 福建德化）如图 1，已知抛物线经过坐标原点 O 和 x 轴上另一点 E，顶点 M 的坐标为 (2,4)；矩 形 ABCD 的顶点 A 与点 O 重合，AD、AB 分别在 x 轴、y 轴上，且 AD=2，AB=3. （1）求该抛物线的函数关系式； （2）将矩形 ABCD 以每秒 1 个单位长度的速度从图 1 所示的位置沿 x 轴的正方向匀速平行移动，同时 一动点 P 也以相同的速度．．．．．从点 A 出发向 B 匀速移动，设它们运动的时间为 t 秒（0≤t≤3），直线 AB 与 该 抛物线的交点为 N（如图 2 所示）. ① 当 t= 2 5 时，判断点 P 是否在直线 ME 上，并说明理由； ② 设以 P、N、C、D 为顶点的多边形面积为 S，试问 S 是否存在最大值？若存在，求出这个最大 值；若不存在，请说明理由． 答案：（1） xxy 42  （2）①点 P 不在直线 ME 上 ②依题意可知：P（t ,t ），N（t ， tt 42  ） 当 30  t 时，以 P、N、C、D 为顶点的多边形是四边形 PNCD，依题意可得： PNCPCD SSS   = ODCD  2 1 + BCPN  2 1 = 232 1  +   242 1 2  ttt = 332  tt 图 2 BC O AD E My x P N · 图 1 BC O (A)D E M y x = 4 21)2 3( 2  t ∵抛物线的开口方向：向下，∴当t = 2 3 ，且 32 30  t 时， 最大S = 4 21 当 03或t 时,点 P、N 都重合，此时以 P、N、C、D 为顶点的多边形是三角形 依题意可得， ABCDSS 矩形2 1 = 322 1  =3 综上所述，以 P、N、C、D 为顶点的多边形面积 S 存在最大值 2、（2010 盐城）已知：函数 y=ax2+x+1 的图象与 x 轴只有一个公共点． （1）求这个函数关系式； （2）如图所示，设二次．．函数 y=ax2+x+1 图象的顶点为 B，与 y 轴的交点为 A，P 为图象上的一点，若以 线段 PB 为直径的圆与直线 AB 相切于点 B，求 P 点的坐标； （3）在(2)中，若圆与 x 轴另一交点关于直线 PB 的对称点为 M，试探索点 M 是否在抛物线 y=ax2+x+1 上，若在抛物线上，求出 M 点的坐标；若不在，请说明理由． 关键词：二次函数与圆 答案 ：1）当a=0时，y=x+1，图象与x轴只有一个公共点………(1分) 当a≠0时，△=1-4a=0，a= 1 4 ，此时，图象与x轴只有一个公共点． ∴函数的解析式为：y=x+1 或`y=1 4 x2+x+1……（3 分） （2）设P 为二次函数图象上的一点，过点P 作PC⊥x 轴于点C． ∵y=ax2+x+1 是二次函数，由（1）知该函数关系式为： y=1 4 x2+x+1，则顶点为 B（-2，0），图象与 y 轴的交点 坐标为 A（0，1）………（4 分） ∵以 PB 为直径的圆与直线 AB 相切于点 B ∴PB⊥AB 则∠PBC=∠BAO ∴Rt△PCB∽Rt△BOA ∴ AO BC OB PC  ，故 PC=2BC，……………………………………………………（5 分） 设 P 点的坐标为(x，y)，∵∠ABO 是锐角，∠PBA 是直角，∴∠PBO 是钝角，∴x<-2 ∴BC=-2-x，PC=-4-2x，即 y=-4-2x， P 点的坐标为(x，-4-2x) ∵点 P 在二次函数 y=1 4 x2+x+1 的图象上，∴-4-2x=1 4 x2+x+1…………………（6 分） A x y OB 解之得：x1=-2，x2=-10 ∵x<-2 ∴x=-10，∴P 点的坐标为：(-10，16)…………………………………（7 分） （3）点 M 不在抛物线y=ax2+x+1 上……………………………………………（8 分） 由（2）知：C 为圆与 x 轴的另一交点，连接 CM，CM 与直线 PB 的交点为 Q，过点 M 作 x 轴的垂线， 垂足为 D，取 CD 的中点 E，连接 QE，则 CM⊥PB，且 CQ=MQ ∴QE∥MD，QE=1 2 MD，QE⊥CE ∵CM⊥PB，QE⊥CE PC⊥x 轴 ∴∠QCE=∠EQB=∠CPB ∴tan∠QCE= tan∠EQB= tan∠CPB =1 2 CE=2QE=2×2BE=4BE，又 CB=8，故 BE=8 5 ，QE=16 5 ∴Q 点的坐标为(-18 5 ，16 5 ) 可求得 M 点的坐标为(14 5 ，32 5 )…………………………………………………（11 分） ∵1 4 (14 5 )2+(14 5 )+1 =144 25 ≠32 5 ∴C 点关于直线 PB 的对称点 M 不在抛物线y=ax2+x+1 上……………………（12 分） (其它解法，仿此得分) 8．(2010 年北京崇文区) 函数 y=x2-2x-2 的图象如右图所示，根据其中提供的信息，可求得使 y≥1 成立 的 x 的取值范围是（ ） A． 31  x B． 31  x C． 31  xx 或 D． 31  xx 或 【关键词】二次函数图象及取值范围 【答案】D 23．(2010 年北京崇文区) 已知 P（ 3,m )和 Q（1，m ）是抛 物 线 22 1y x bx   上的两点． （1）求b 的值； （2）判断关于 x 的一元二次方程 22 1x bx  =0 是否有实数根，若有，求出它的实数根；若没有， 请说明理由； （3）将抛物线 22 1y x bx   的图象向上平移 k （ k 是正整数）个单位，使平移后的图象与 x 轴无 交点，求 k 的最小值． 【关键词】求二次函数解析式、与 X 轴交点个数、平移 【答案】解：(1)因为点 P、Q 在抛物线上且纵坐标相同，所以 P、Q 关于抛物线对称轴对称并且到对 称轴距离相等． 所以，抛物线对称轴 3 1 4 2 bx     ，所以， 4b  ．[来源:www.shulihua.net] （2）由（1）可知，关于 x 的一元二次方程为 22 4 1x x  =0． 因为， 2 4b ac  =16-8=8  0． 所以，方程有两个不同的实数根，分别是 1 212 2 bx a      ， 2 212 2 bx a      ． （3）由（1）可知，抛物线 22 4 1y x x   的图象向上平移 k （ k 是正整数）个单位后的解析式为 22 4 1y x x k    ． 若使抛物线 22 4 1y x x k    的图象与 x 轴无交点，只需 22 4 1 0x x k    无实数解即 可． 由 2 4b ac  =16 8(1 )k  =8 8k <0，得 1k  又 k 是正整数，所以 k 得最小值为 2． 2５．(2010 年北京崇文区) 已知抛物线 2 1y ax bx   经过点 A（1，3）和点 B（2，1）． （1）求此抛物线解析式； （2）点 C、D 分别是 x 轴和 y 轴上的动点，求四边形 ABCD 周长的最小值； （3）过点 B 作 x 轴的垂线，垂足为 E 点．点 P 从抛物线的顶点出发，先沿抛物线的对称轴到达 F 点, 再沿 FE 到达 E 点，若 P 点在对称轴上的运动速度是它在直线 FE 上运动速度的 2 倍,试确定点 F 的位置, 使得点 P 按照上述要求到达 E 点所用的时间最短．（要求：简述确定 F 点位置的方法，但不要求证明） 【关键词】二次函数与动点 【答案】解：（1）依题意： 3 1, 1 4 2 1. a b a b        解得 2, 4. a b     抛物线的解析式为 22 4 1y x x    ． （2）点 A（1，3）关于 y 轴的对称点 A的坐标是（-1，3），点 B（2，1）关于 x 轴的对称点 B的坐标 是（2，-1）．由对称性可知 AB BC CD DA   = ' 'AB B C CD DA    AB A B  由勾股定理可求 AB= 5 ， 5A B   ． 所以，四边形 ABCD 周长的最小值是 5 5AB A B    ． （3）确定 F 点位置的方法：过点 E 作直线 EG 使对称轴到直线 EG 成 45角，则 EG 与对称轴的交点为 所求的 F 点． 设对称轴于 x 轴交于点 H，在 Rt HEF 中，由 HE=1， 90 , 45FHE EFH      ，得 HF=1．所以， 点 F 的坐标是（1，1）． 23．（2010 年门头沟区）已知：关于 x 的一元二次方程 01)2()1( 2  xmxm （m 为实数） （1）若方程有两个不相等的实数根，求 m 的取值范围； （2）在（1）的条件下，求证：无论 m 取何值，抛物线 1)2()1( 2  xmxmy 总过 x 轴上的一 个固定点； （3）若 m 是整数，且关于 x 的一元二次方程 01)2()1( 2  xmxm 有两个不相等的整数根，把 抛物线 1)2()1( 2  xmxmy 向右平移 3 个单位长度，求平移后的解析式． 【关键词】二次函数与一元二次方程 【答案】解：（1）△= 22 )1(4)2( mmm  ∵方程有两个不相等的实数根, ∴ 0m .………………………………………………………………………………1 分 ∵ 01 m , ∴m 的取值范围是 1,0  mm 且 .…………………………………………………2 分 （2）证明：令 0y 得， 01)2()1( 2  xmxm . ∴ )1(2 )2( )1(2 )2( 2    m mm m mmx .[来源:www.shulihua.netwww.shulihua.net] ∴ 1)1(2 2 1   m mmx ， 1 1 )1(2 2 2   mm mmx . …………………………………4 分 ∴抛物线与 x 轴的交点坐标为（ 0,1 ），（ 0,1 1 m ）, ∴无论 m 取何值，抛物线 1)2()1( 2  xmxmy 总过定点（ 0,1 ）.…5 分 （3）∵ 1x 是整数 ∴只需 1 1 m 是整数. ∵ m 是整数，且 1,0  mm , ∴ 2m .……………………………………………………………………………6 分 当 2m 时，抛物线为 12  xy ． 把它的图象向右平移 3 个单位长度，得到的抛物线解析式为 861)3( 22  xxxy .……………………………………………………7 分 24．（2010 年门头沟区）如图，已知抛物线 C1： 5)2( 2  xay 的顶点为 P，与 x 轴相交于 A、B 两点（点 A 在点 B 的左边），点 A 的横坐标是 1 ． （1）求 p 点坐标及 a 的值； （2）如图（1），抛物线 C2 与抛物线 C1 关于 x 轴对称，将抛物线 C2 向左平移，平移后的抛物线记为 C3， C3 的 顶 点 为 M ， 当 点 P 、 M 关 于 点 A 成 中 心 对 称 时 ， 求 C3 的 解 析 式 khxay  2)( ； [ 来 源:www.shulihua.netwww.shulihua.net] （3）如图（2），点 Q 是 x 轴负半轴上一动点，将抛物线 C1 绕点 Q 旋转 180° 后得到抛物线 C4．抛物线 C4 的顶点为 N，与 x 轴相交于 E、F 两点（点 E 在点 F 的左边），当以点 P、N、E 为顶点的三角形是直角三 角形时，求顶点 N 的坐标． 【关键词】二次函数、平衡、旋转 【答案】解：（1）由抛物线 C1： 5)2( 2  xay 得顶点 P 的坐标为（2，5）…….1 分 ∵点 A（－1，0）在抛物线 C1 上∴ 9 5a  .………………2 分 （2）连接 PM，作 PH⊥x 轴于 H，作 MG⊥x 轴于 G.. ∵点 P、M 关于点 A 成中心对称, ∴PM 过点 A，且 PA＝MA.. ∴△PAH≌△MAG.. ∴MG＝PH＝5，AG＝AH＝3. ∴顶点 M 的坐标为（ 4 ，5）.…………………3 分 ∵抛物线 C2 与 C1 关于 x 轴对称，抛物线 C3 由 C2 平移得到 ∴抛物线 C3 的表达式 5)4(9 5 2  xy . ………4 分 （3）∵抛物线 C4 由 C1 绕 x 轴上的点 Q 旋转 180°得到 ∴顶点 N、P 关于点 Q 成中心对称. 由（2）得点 N 的纵坐标为 5. 设点 N 坐标为（m，5），作 PH⊥x 轴于 H，作 NG⊥x 轴于 G，作 PR⊥NG 于 R. ∵旋转中心 Q 在 x 轴上, ∴EF＝AB＝2AH＝6. ∴EG＝3，点 E 坐标为（ 3m  ，0），H 坐标为（2，0），R 坐标为（m，－5）. 根据勾股定理，得 ,104m4mPRNRPN 2222  50m10mHEPHPE 2222  G C1 N FE HA BQ y x 3435NE 222  ①当∠PNE＝90º时，PN2+ NE2＝PE2， 解得 m＝ 3 44 ，∴N 点坐标为（ 3 44 ，5） ②当∠PEN＝90º时，PE2+ NE2＝PN2， 解得 m＝ 3 10 ，∴N 点坐标为（ 3 10 ，5）. ③∵PN＞NR＝10＞NE，∴∠NPE≠90º ……7 分 综上所得，当 N 点坐标为（ 3 44 ，5）或（ 3 10 ，5）时，以点 P、N、E 为顶点的三角形是直角三角 形．……………………8 分 说明：点 N 的坐标都求正确给 8 分，不讨论③不扣分． 1. （2010 年山东省济南市）在平面直角坐标系中，抛物线 2 1y x  与 x 轴的交点的个数是（ ） A．3 B．2 C．1 D．0 【关键词】二次函数与坐标轴的交点 【答案】B 2.（2010 年台湾省）坐标平面上有一函数 y=24x248 的图形，其顶点坐标为何？ (A) (0，2) (B) (1，24) (C) (0，48) (D) (2，48) 【关键词】二次函数的顶点 【答案】C 3. （2010 年台湾省）坐标平面上，若移动二次函数 y=2(x175)(x176)6 的图形，使其与 x 轴交于两点， 且此两点的距离为 1 单位，则移动方式可为下列哪一种？ (A) 向上移动 3 单位 (B) 向下移动 3 单位 (C) 向上移勤 6 单位 (D) 向下移动 6 单位 【关键词】二次函数的平移 【答案】D 4.（2010 年山东省济南市）如图，已知抛物线 2y x bx c   经过点（1，-5）和（-2，4） （1）求这条抛物线的解析式． （ 2 ） 设 此 抛 物 线 与 直 线 y x 相 交 于 点 A ， B （ 点 B 在 点 A 的 右 侧 ）， 平 行 于 y 轴 的 直 线  0 5 1x m m    与抛 物线交于点 M，与直线 y x 交于点 N，交 x 轴于点 P，求线段 MN 的长（用 含 m 的代数式表示）． （3）在条件（2）的情 况下，连接 OM、BM，是否 存在 m 的值，使△BOM 的面积 S 最大？若存在，请求 出 m 的值，若不存在， 请说明理由． xO P N M B A y y=x x=m 【关键词】二次函数 【答案】 21．（2010 山东德州）为迎接第四届世界太阳城大会，德州市把主要路段路灯更换为太阳能路灯．已知太 阳能路灯售价为 5000 元/个，目前两个商家有此产品．甲商家用如下方法促销：若购买路灯不超过 100 个，按原价付款；若一次购买 100 个以上，且购买的个数每增加一个，其价格减少 10 元，但太阳能路 灯的售价不得低于 3500 元/个．乙店一律按原价的 80℅销售．现购买太阳能路灯 x 个，如果全部在甲商 家购买，则所需金额为 y1 元；如果全部在乙商家购买，则所需金额为 y2 元. （1）分别求出 y1、y2 与 x 之间的函数关系式； （2）若市政府投资 140 万元，最多能购买多少个太阳能路灯？ 【关键词】二次函数、一次函数、方案设计 【答案】解：（1）由题意可知， 当 x≤100 时，购买一个需 5000 元，故 1 5000y x ； 当 x≥100 时，因为购买个数每增加一个，其价格减少 10 元，但售价不得低于 3500 元/个，所以 x≤ 10 35005000  +100=250． 即 100≤x≤250 时，购买一个需 5000-10(x-100)元，故 y1=6000x-10x2； 当 x>250 时，购买一个需 3500 元，故 1 3500y x ； 所以，     x xx x y 3500 106000 5000 2 1 ).250( )250100( )1000(    x x x ， ， 2 5000 80% 4000y x x   ． (2) 当 0