九下数学直棱柱和圆锥侧面图教学课件 26页

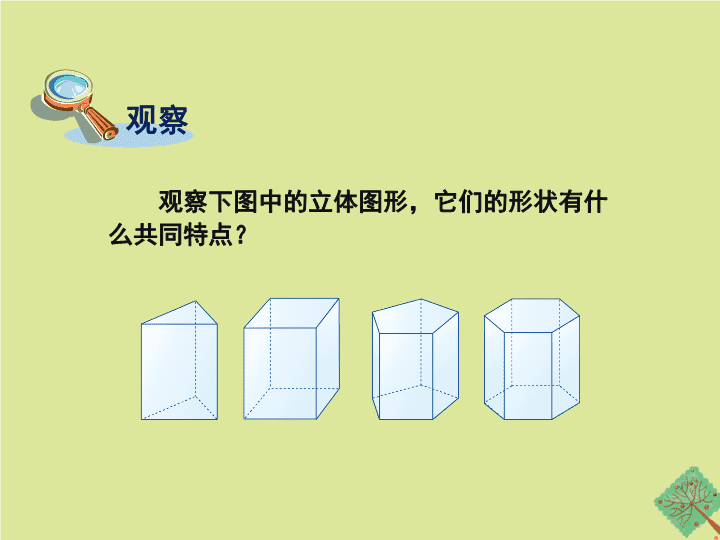
直棱柱和圆锥的侧面展开图 观察下图中的立体图形，它们的形状有什么共同特点？ 观察 在几何中，我们把上述这样的立体图形称为 直棱柱 ，其中“棱”是指两个面的公共边，它具有以下特征： （ 1 ） 有两个面互相平行，称它们为底面； （ 2 ）其余各个面均为矩形，称它们为侧面； （ 3 ）侧棱（指两个侧面的公共边）垂直于底面 . 根据底面图形的边数，我们分别称图中的立体 图形为直三棱柱、直四棱柱、直五棱柱、直六棱柱 . 例如，长方体和正方体都是直四棱柱 . 底面是正多边 形的棱柱叫作正棱柱 . 收集几个直棱柱模型，再把侧面沿 一条侧棱剪开，它们的侧面能否展开成 平面图形，是矩形吗？ 做一做 甲 展开 展开 棱柱的表面展开图 展开 五棱柱 展开 六棱柱 将直棱柱的侧面沿着一条侧棱剪开，可以 展开成平面图形，像这样的平面图形称为 直棱 柱的侧面展开图 . 如下图所示是一个直四棱柱的 侧面展开图 . 直棱柱的侧面展开图是一个矩形，这个 矩形的长是直棱柱的底面周长，宽是直棱柱 的侧棱长（高） . 一个食品包装盒的侧面展开图如图所示，它的 底面是边长为 2 的正六边形，这个包装盒是什么 形状的几何体？试根据已知数据求出它的侧面积 . 举 例 例 1 解 根据图示可知该包装盒的侧面是矩形，又已知上、下底面是正六边形，因此这个几何体是正六棱柱（如图所示） . 由已知数据可知它的底面周长为 2×6=12 ， 因此它的侧面积为 12×6=72. 观察 下图是雕塑与斗笠的形象，它们的形状有什么特点？ 在几何中，我们把上述这样的立体图形称为 圆锥 ，圆锥是由一个底面和一个侧面围成的图形， 它的底面是一个圆，连接顶点与底面圆心的线段 叫作圆锥的 高 ，圆锥顶点与底面圆上任意一点的 连线段都叫作圆锥的 母线 ，母线的长度均相等 . 如图， PO 是圆锥的高， PA 是母线 . 把圆锥沿它的一条母线剪开，它的侧面可以展开成平面图形，像这样的平面图形称为圆锥的侧面展开图，如图所示 . 圆锥的侧面展开图是一个扇形 . 这个扇形的半径是圆锥的母线长 PA ，弧长是圆锥底面圆的周长 . P A 如图，小刚用一张半径为 24cm 的扇形纸板做一个 圆锥形帽子（接缝忽略不计），如果做成的圆锥 形帽子的底面半径为 10cm ，那么这张扇形纸板的 面积 S 是多少？ 举 例 例 2 分析 圆锥形帽子的底面周长就是扇形的弧长 . 解 扇形的弧长（即底面圆周长）为 所以扇形纸板的面积 练习 1. 某个立体图形的侧面展开图如图所示，它的 底面是正三角形，那么这个立体图形是（ ） （ A ）三棱柱 （ B ）四棱柱 （ C ）三棱锥 . A 2. 如图，上面的图形分别是下面哪个立体图形展开的形状？把它们用线连起来。 3. 如图为一直三棱柱，试画出它的侧面展开图， 并求侧面展开图的面积 . 2.5 2 1.5 3 答：它的侧面展开图为 S = 3×(2.5+2+1.5)=18. 4. 如图，圆锥的顶点为 P ， AB 是底面⊙ O 的一条 直径， ∠ APB =90° ，底面半径为 r ，求这个圆 锥的侧面积和表面积 . 解：根据题意易知扇形的弧长（即底面圆周长）为 ； 扇形的半径为 所以圆锥的侧面积 圆锥的表面积 A C B C” （ C ） C’ （ C ） 4cm 如图，有一边长 4 米立方体形的房间，一只蜘蛛在 A 处，一只苍蝇在 B 处。⑴试问，蜘蛛去抓苍蝇需要爬行的最短路程是多少？ ⑵若苍蝇在 C 处，则最短路程是多少？ 4cm 探索 A B C 6cm 4cm 如果换成长方体纸盒又会怎么样呢？ 4cm C ´´ C ´ E F D G ´ H G E ´ 棒 你 太 棒 了 ！ 们 KEY : 如果“你”在前面，那么谁在后面？ 等你来挑战 ! 1. 如图是一个立方体纸盒的展开图，使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数 , 求 : -2 -7 1 当堂训练 2. 利 胜 持 是 就 坚 “坚”在下，“就”在后，胜利在哪里？ “胜”在上， “利”在前！ 如图，长方体的长为 15cm ，宽为 10cm ，高为 20cm ，点 B 到点 C 的距离为 5cm ，一只蚂蚁如果要沿着长方体的表面从 A 点爬到 B 点，需要爬行的最短距离是多少？ 20 10 15 B C A 3 .