2018年四川省自贡市中考数学试卷含答案 20页

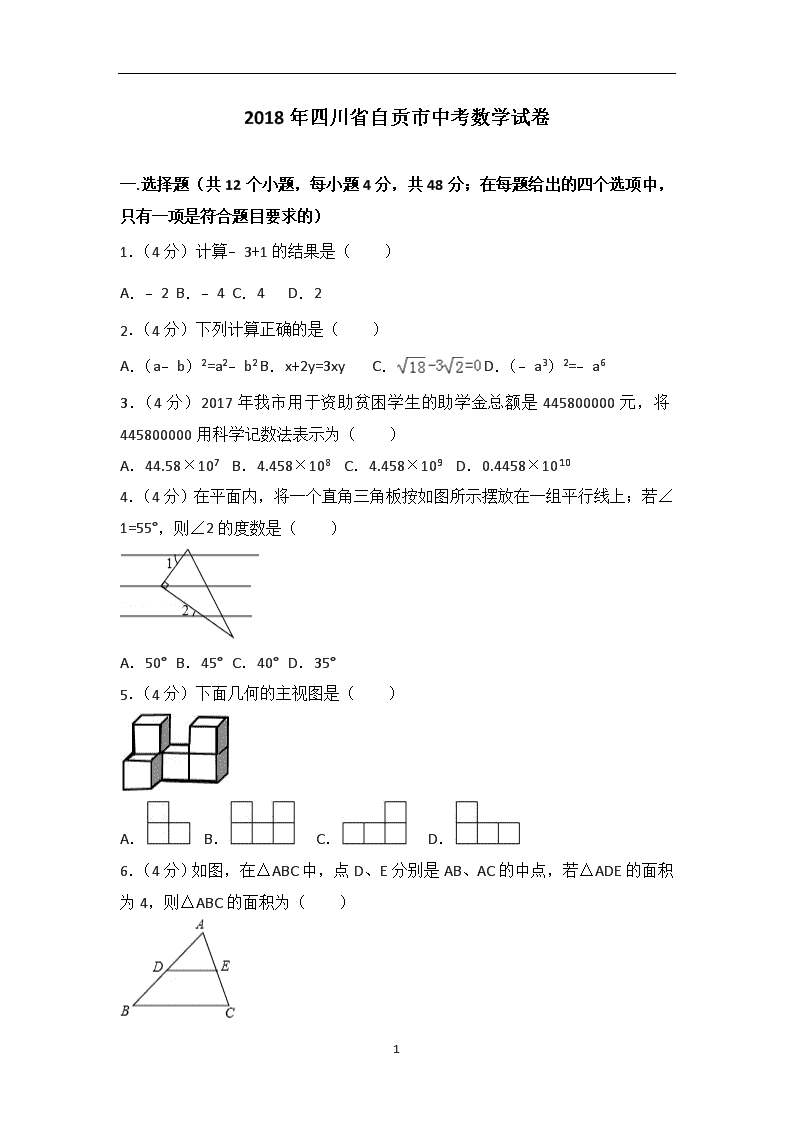
‎2018年四川省自贡市中考数学试卷 ‎　‎ 一.选择题（共12个小题，每小题4分，共48分；在每题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（4分）计算﹣3+1的结果是（　　）‎ A．﹣2 B．﹣4 C．4 D．2‎ ‎2．（4分）下列计算正确的是（　　）‎ A．（a﹣b）2=a2﹣b2 B．x+2y=3xy C． D．（﹣a3）2=﹣a6‎ ‎3．（4分）2017年我市用于资助贫困学生的助学金总额是445800000元，将445800000用科学记数法表示为（　　）‎ A．44.58×107 B．4.458×108 C．4.458×109 D．0.4458×1010‎ ‎4．（4分）在平面内，将一个直角三角板按如图所示摆放在一组平行线上；若∠1=55°，则∠2的度数是（　　）‎ A．50° B．45° C．40° D．35°‎ ‎5．（4分）下面几何的主视图是（　　）‎ A． B． C． D．‎ ‎6．（4分）如图，在△ABC中，点D、E分别是AB、AC的中点，若△ADE的面积为4，则△ABC的面积为（　　）‎ 20‎ A．8 B．12 C．14 D．16‎ ‎7．（4分）在一次数学测试后，随机抽取九年级（3）班5名学生的成绩（单位：分）如下：80、98、98、83、91，关于这组数据的说法错误的是（　　）‎ A．众数是98 B．平均数是90 C．中位数是91 D．方差是56‎ ‎8．（4分）回顾初中阶段函数的学习过程，从函数解析式到函数图象，再利用函数图象研究函数的性质，这种研究方法主要体现的数学思想是（　　）‎ A．数形结合 B．类比 C．演绎 D．公理化 ‎9．（4分）如图，若△ABC内接于半径为R的⊙O，且∠A=60°，连接OB、OC，则边BC的长为（　　）‎ A． B． C． D．‎ ‎10．（4分）从﹣1、2、3、﹣6这四个数中任取两数，分别记为m、n，那么点（m，n）在函数y=图象的概率是（　　）‎ A． B． C． D．‎ ‎11．（4分）已知圆锥的侧面积是8πcm2，若圆锥底面半径为R（cm），母线长为l（cm），则R关于l的函数图象大致是（　　）‎ A． B． C． D．‎ ‎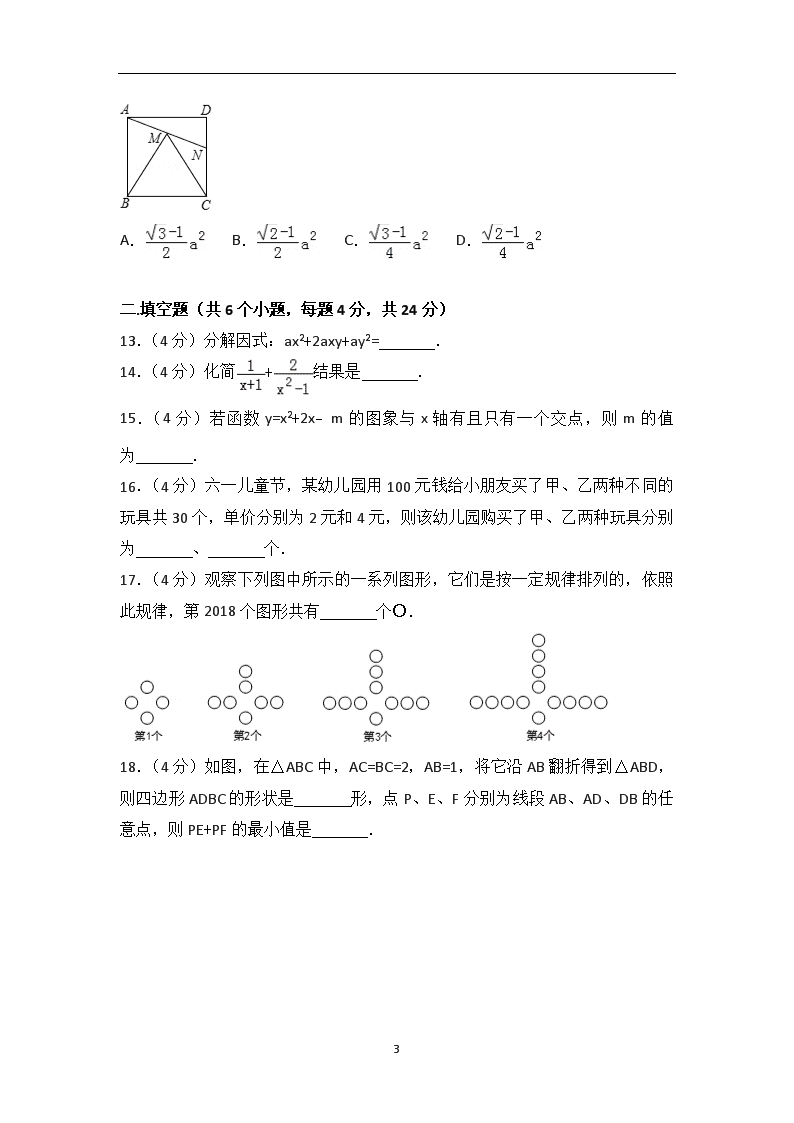12．（4分）如图，在边长为a正方形ABCD中，把边BC绕点B逆时针旋转60°，得到线段BM，连接AM并延长交CD于N，连接MC，则△MNC的面积为（　　）‎ 20‎ A． B． C． D．‎ ‎　‎ 二.填空题（共6个小题，每题4分，共24分）‎ ‎13．（4分）分解因式：ax2+2axy+ay2=　 　．‎ ‎14．（4分）化简+结果是　 　．‎ ‎15．（4分）若函数y=x2+2x﹣m的图象与x轴有且只有一个交点，则m的值为　 　．‎ ‎16．（4分）六一儿童节，某幼儿园用100元钱给小朋友买了甲、乙两种不同的玩具共30个，单价分别为2元和4元，则该幼儿园购买了甲、乙两种玩具分别为　 　、　 　个．‎ ‎17．（4分）观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2018个图形共有　 　个○．‎ ‎18．（4分）如图，在△ABC中，AC=BC=2，AB=1，将它沿AB翻折得到△ABD，则四边形ADBC的形状是　 　形，点P、E、F分别为线段AB、AD、DB的任意点，则PE+PF的最小值是　 　．‎ 20‎ ‎　‎ 三、解答题（共8个题，共78分）‎ ‎19．（8分）计算：|﹣|+（）﹣1﹣2cos45°．‎ ‎20．（8分）解不等式组：，并在数轴上表示其解集．‎ ‎21．（8分）某校研究学生的课余爱好情况吧，采取抽样调查的方法，从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好，并将调查结果绘制成下面两幅不完整的统计图，请你根据图中提供的信息解答下列问题：‎ ‎（1）在这次调查中，一共调查了　 　名学生；‎ ‎（2）补全条形统计图；‎ ‎（3）若该校共有1500名，估计爱好运动的学生有　 　人；‎ ‎（4）在全校同学中随机选取一名学生参加演讲比赛，用频率估计概率，则选出的恰好是爱好阅读的学生的概率是　 　．‎ ‎22．（8分）如图，在△ABC中，BC=12，tanA=，∠‎ 20‎ B=30°；求AC和AB的长．‎ ‎23．（10分）如图，在△ABC中，∠ACB=90°．‎ ‎（1）作出经过点B，圆心O在斜边AB上且与边AC相切于点E的⊙O（要求：用尺规作图，保留作图痕迹，不写作法和证明）‎ ‎（2）设（1）中所作的⊙O与边AB交于异于点B的另外一点D，若⊙O的直径为5，BC=4；求DE的长．（如果用尺规作图画不出图形，可画出草图完成（2）问）‎ ‎24．（10分）阅读以下材料：‎ 对数的创始人是苏格兰数学家纳皮尔（J．Nplcr，1550﹣1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707﹣1783年）才发现指数与对数之间的联系．‎ 对数的定义：一般地，若ax=N（a＞0，a≠1），那么x叫做以a为底N的对数，记作：x=logaN．比如指数式24=16可以转化为4=log216，对数式2=log525可以转化为52=25．‎ 我们根据对数的定义可得到对数的一个性质：loga（M•N）=logaM+logaN（a＞0，a≠1，M＞0，N＞0）；理由如下：‎ 设logaM=m，logaN=n，则M=am，N=an ‎∴M•N=am•an=am+n，由对数的定义得m+n=loga（M•N）‎ 又∵m+n=logaM+logaN ‎∴loga（M•N）=logaM+logaN 解决以下问题：‎ ‎（1）将指数43=64转化为对数式　 　；‎ 20‎ ‎（2）证明loga=logaM﹣logaN（a＞0，a≠1，M＞0，N＞0）‎ ‎（3）拓展运用：计算log32+log36﹣log34=　 　．‎ ‎25．（12分）如图，已知∠AOB=60°，在∠AOB的平分线OM上有一点C，将一个120°角的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E．‎ ‎（1）当∠DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OE+OD与OC的数量关系，并说明理由；‎ ‎（2）当∠DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；‎ ‎（3）当∠DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明．‎ ‎26．（14分）如图，抛物线y=ax2+bx﹣3过A（1，0）、B（﹣3，0），直线AD交抛物线于点D，点D的横坐标为﹣2，点P（m，n）是线段AD上的动点．‎ ‎（1）求直线AD及抛物线的解析式；‎ ‎（2）过点P的直线垂直于x轴，交抛物线于点Q，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？‎ ‎（3）在平面内是否存在整点（横、纵坐标都为整数）R，使得P、Q、D、R为顶点的四边形是平行四边形？若存在，直接写出点R的坐标；若不存在，说明理由．‎ 20‎ ‎　‎ 20‎ ‎2018年四川省自贡市中考数学试卷 参考答案与试题解析 ‎　‎ 一.选择题（共12个小题，每小题4分，共48分；在每题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．‎ ‎【解答】解：﹣3+1=﹣2；‎ 故选：A．‎ ‎　‎ ‎2．‎ ‎【解答】解：（A）原式=a2﹣2ab+b2，故A错误；‎ ‎（B）原式=x+2y，故B错误；‎ ‎（D）原式=a6，故D错误；‎ 故选：C．‎ ‎　‎ ‎3．‎ ‎【解答】解：445800000=4.458×108，‎ 故选：B．‎ ‎　‎ ‎4．‎ ‎【解答】解：由题意可得：∠1=∠3=55°，‎ ‎∠2=∠4=90°﹣55°=35°．‎ 故选：D．‎ ‎　‎ 20‎ ‎5．‎ ‎【解答】解：从几何体正面看，从左到右的正方形的个数为：2，1，2．故选B．‎ ‎　‎ ‎6．‎ ‎【解答】解：∵在△ABC中，点D、E分别是AB、AC的中点，‎ ‎∴DE∥BC，DE=BC，‎ ‎∴△ADE∽△ABC，‎ ‎∵=，‎ ‎∴=，‎ ‎∵△ADE的面积为4，‎ ‎∴△ABC的面积为：16，‎ 故选：D．‎ ‎　‎ ‎7．‎ ‎【解答】解：98出现的次数最多，‎ ‎∴这组数据的众数是98，A说法正确；‎ ‎=（80+98+98+83+91）=90，B说法正确；‎ 这组数据的中位数是91，C说法正确；‎ S2=[（80﹣90）2+（98﹣90）2+（98﹣90）2+（83﹣90）2+（91﹣90）2]‎ ‎=×278‎ ‎=55.6，D说法错误；‎ 故选：D．‎ ‎　‎ ‎8．‎ ‎【解答】‎ 20‎ 解：学习了一次函数、二次函数和反比例函数，都是按照列表、描点、连线得到函数的图象，然后根据函数的图象研究函数的性质，这种研究方法主要体现了数形结合的数学思想．‎ 故选：A．‎ ‎　‎ ‎9．‎ ‎【解答】解：延长BO交⊙O于D，连接CD，‎ 则∠BCD=90°，∠D=∠A=60°，‎ ‎∴∠CBD=30°，‎ ‎∵BD=2R，‎ ‎∴DC=R，‎ ‎∴BC=R，‎ 故选：D．‎ ‎　‎ ‎10．‎ ‎【解答】解：∵点（m，n）在函数y=的图象上，‎ ‎∴mn=6．‎ 列表如下：‎ m ‎﹣1‎ ‎﹣1‎ ‎﹣1‎ ‎2‎ ‎2‎ ‎2‎ ‎3‎ ‎3‎ ‎3‎ ‎﹣6‎ ‎﹣6‎ ‎﹣6‎ n ‎2‎ ‎3‎ ‎﹣6‎ ‎﹣1‎ ‎3‎ ‎﹣6‎ ‎﹣1‎ ‎2‎ ‎﹣6‎ ‎﹣1‎ ‎2‎ ‎3‎ mn ‎﹣2‎ ‎﹣3‎ ‎6‎ ‎﹣2‎ ‎6‎ ‎﹣12‎ ‎﹣3‎ ‎6‎ ‎﹣18‎ ‎6‎ ‎﹣12‎ ‎﹣18‎ mn的值为6的概率是=．‎ 故选：B．‎ ‎　‎ ‎11．‎ ‎【解答】解：由题意得，lR=8π，‎ 20‎ 则R=，‎ 故选：A．‎ ‎　‎ ‎12．‎ ‎【解答】解：作MG⊥BC于G，MH⊥CD于H，‎ 则BG=GC，AB∥MG∥CD，‎ ‎∴AM=MN，‎ ‎∵MH⊥CD，∠D=90°，‎ ‎∴MH∥AD，‎ ‎∴NH=HD，‎ 由旋转变换的性质可知，△MBC是等边三角形，‎ ‎∴MC=BC=a，‎ 由题意得，∠MCD=30°，‎ ‎∴MH=MC=a，CH=a，‎ ‎∴DH=a﹣a，‎ ‎∴CN=CH﹣NH=a﹣（a﹣a）=（﹣1）a，‎ ‎∴△MNC的面积=××（﹣1）a=a2，‎ 故选：C．‎ ‎　‎ 二.填空题（共6个小题，每题4分，共24分）‎ ‎13．‎ ‎【解答】解：原式=a（x2+2xy+y2）…（提取公因式）‎ ‎=a（x+y）2．…（完全平方公式）‎ ‎　‎ 20‎ ‎14．‎ ‎【解答】解：原式=+‎ ‎=‎ 故答案为：‎ ‎　‎ ‎15．‎ ‎【解答】解：∵函数y=x2+2x﹣m的图象与x轴有且只有一个交点，‎ ‎∴△=22﹣4×1×（﹣m）=0，‎ 解得：m=﹣1．‎ 故答案为：﹣1．‎ ‎　‎ ‎16．‎ ‎【解答】解：设甲玩具购买x个，乙玩具购买y个，由题意，得 ‎，‎ 解得，‎ 甲玩具购买10个，乙玩具购买20个，‎ 故答案为：10，20．‎ ‎　‎ ‎17．‎ ‎【解答】解：‎ 观察图形可知：‎ 第1个图形共有：1+1×3，‎ 第2个图形共有：1+2×3，‎ 第3个图形共有：1+3×3，‎ ‎…，‎ 第n个图形共有：1+3n，‎ 20‎ ‎∴第2018个图形共有1+3×2018=6055，‎ 故答案为：6055．‎ ‎　‎ ‎18．‎ ‎【解答】解：∵△ABC沿AB翻折得到△ABD，‎ ‎∴AC=AD，BC=BD，‎ ‎∵AC=BC，‎ ‎∴AC=AD=BC=BD，‎ ‎∴四边形ADBC是菱形，‎ 故答案为菱；‎ 如图 作出F关于AB的对称点M，再过M作ME⊥AD，交ABA于点P，此时PE+PF最小，此时PE+PF=ME，‎ 过点A作AN⊥BC，‎ ‎∵AD∥BC，‎ ‎∴ME=AN，‎ 作CH⊥AB，‎ ‎∵AC=BC，‎ ‎∴AH=，‎ 由勾股定理可得，CH=，‎ ‎∵，‎ 20‎ 可得，AN=，‎ ‎∴ME=AN=，‎ ‎∴PE+PF最小为，‎ 故答案为．‎ ‎　‎ 三、解答题（共8个题，共78分）‎ ‎19．‎ ‎【解答】解：原式=+2﹣2×‎ ‎=+2﹣‎ ‎=2．‎ 故答案为2．‎ ‎　‎ ‎20．‎ ‎【解答】解：解不等式①，得：x≤2；‎ 解不等式②，得：x＞1，‎ ‎∴不等式组的解集为：1＜x≤2．‎ 将其表示在数轴上，如图所示．‎ ‎　‎ ‎21．‎ ‎【解答】解：（1）爱好运动的人数为40，所占百分比为40%‎ ‎∴共调查人数为：40÷40%=100‎ ‎（2）爱好上网的人数所占百分比为10%‎ ‎∴爱好上网人数为：100×10%=10，‎ ‎∴爱好阅读人数为：100﹣40﹣20﹣10=30，‎ 补全条形统计图，如图所示，‎ 20‎ ‎（3）爱好运动所占的百分比为40%，‎ ‎∴估计爱好运用的学生人数为：1500×40%=600‎ ‎（4）爱好阅读的学生人数所占的百分比40%，‎ ‎∴用频率估计概率，则选出的恰好是爱好阅读的学生的概率为 故答案为：（1）100；（3）600；（4）‎ ‎　‎ ‎22．‎ ‎【解答】解：如图作CH⊥AB于H．‎ 在Rt△BCH中，∵BC=12，∠B=30°，‎ ‎∴CH=BC=6，BH==6，‎ 在Rt△ACH中，tanA==，‎ ‎∴AH=8，‎ ‎∴AC==10，‎ ‎∴AB=AH+BH=8+6．‎ ‎　‎ ‎23．‎ ‎【解答】解：（1）⊙O如图所示；‎ 20‎ ‎（2）作OH⊥BC于H．‎ ‎∵AC是⊙O的切线，‎ ‎∴OE⊥AC，‎ ‎∴∠C=∠CEO=∠OHC=90°，‎ ‎∴四边形ECHO是矩形，‎ ‎∴OE=CH=，BH=BC﹣CH=，‎ 在Rt△OBH中，OH==2，‎ ‎∴EC=OH=2，BE==2，‎ ‎∵∠EBC=∠EBD，∠BED=∠C=90°，‎ ‎∴△BCE∽△BED，‎ ‎∴=，‎ ‎∴=，‎ ‎∴DE=．‎ ‎　‎ ‎24．‎ ‎【解答】解：（1）由题意可得，指数式43=64写成对数式为：3=log464，‎ 故答案为：3=log464；‎ ‎（2）设logaM=m，logaN=n，则M=am，N=an，‎ ‎∴==am﹣n，由对数的定义得m﹣n=loga，‎ 又∵m﹣n=logaM﹣logaN，‎ 20‎ ‎∴loga=logaM﹣logaN（a＞0，a≠1，M＞0，N＞0）；‎ ‎（3）log32+log36﹣log34，‎ ‎=log3（2×6÷4），‎ ‎=log33，‎ ‎=1，‎ 故答案为：1．‎ ‎　‎ ‎25．‎ ‎【解答】解：（1）∵OM是∠AOB的角平分线，‎ ‎∴∠AOC=∠BOC=∠AOB=30°，‎ ‎∵CD⊥OA，‎ ‎∴∠ODC=90°，‎ ‎∴∠OCD=60°，‎ ‎∴∠OCE=∠DCE﹣∠OCD=60°，‎ 在Rt△OCD中，OD=OE•cos30°=OC，‎ 同理：OE=OC，‎ ‎∴OD+OD=OC；‎ ‎（2）（1）中结论仍然成立，理由：‎ 过点C作CF⊥OA于F，CG⊥OB于G，‎ ‎∴∠OFC=∠OGC=90°，‎ ‎∵∠AOB=60°，‎ ‎∴∠FCG=120°，‎ 同（1）的方法得，OF=OC，OG=OC，‎ ‎∴OF+OG=OC，‎ ‎∵CF⊥OA，CG⊥OB，且点C是∠AOB的平分线OM上一点，‎ ‎∴CF=CG，‎ 20‎ ‎∵∠DCE=120°，∠FCG=120°，‎ ‎∴∠DCF=∠ECG，‎ ‎∴△CFD≌△CGE，‎ ‎∴DF=EG，‎ ‎∴OF=OD+DF=OD+EG，OG=OE﹣EG，‎ ‎∴OF+OG=OD+EG+OE﹣EG=OD+OE，‎ ‎∴OD+OE=OC；‎ ‎（3）（1）中结论不成立，结论为：OE﹣OD=OC，‎ 理由：过点C作CF⊥OA于F，CG⊥OB于G，‎ ‎∴∠OFC=∠OGC=90°，‎ ‎∵∠AOB=60°，‎ ‎∴∠FCG=120°，‎ 同（1）的方法得，OF=OC，OG=OC，‎ ‎∴OF+OG=OC，‎ ‎∵CF⊥OA，CG⊥OB，且点C是∠AOB的平分线OM上一点，‎ ‎∴CF=CG，∵∠DCE=120°，∠FCG=120°，‎ ‎∴∠DCF=∠ECG，‎ ‎∴△CFD≌△CGE，‎ ‎∴DF=EG，‎ ‎∴OF=DF﹣OD=EG﹣OD，OG=OE﹣EG，‎ ‎∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD，‎ 20‎ ‎∴OE﹣OD=OC．‎ ‎　‎ ‎26．‎ ‎【解答】解：（1）把（1，0），（﹣3，0）代入函数解析式，得 ‎，‎ 解得，‎ 抛物线的解析式为y=x2+2x﹣3；‎ 当x=﹣2时，y=（﹣2）2+2×（﹣2）﹣3，解得y=﹣3，‎ 即D（﹣2，﹣3）．‎ 设AD的解析式为y=kx+b，将A（1，0），D（﹣2，﹣3）代入，得 ‎，‎ 解得，‎ 直线AD的解析式为y=x﹣1；‎ ‎（2）设P点坐标为（m，m﹣1），Q（m，m2+2m﹣3），‎ l=（m﹣1）﹣（m2+2m﹣3）‎ 化简，得 l=﹣m2﹣m+2‎ 配方，得 l=﹣（m+）2+，‎ 当m=﹣时，l最大=；‎ ‎（3）DR∥PQ且DR=PQ时，PQDR是平行四边形，‎ 由（2）得0＜PQ≤，‎ 又PQ是正整数，‎ ‎∴PQ=1，或PQ=2．‎ 20‎ 当PQ=1时，DR=1，﹣3+1=﹣2，即R（﹣2，﹣2），‎ ‎﹣3﹣1=﹣4，即R（﹣2，﹣4）；‎ 当PQ=2时，DR=2，﹣3+2=﹣1，即R（﹣2，﹣1），‎ ‎﹣3﹣2=﹣5，即R（﹣2，﹣5），‎ 综上所述：R点的坐标为（﹣2，﹣2），（﹣2，﹣4），（﹣2，﹣1）（﹣2，﹣5），使得P、Q、D、R为顶点的四边形是平行四边形．‎ ‎　‎ 20‎