鄂尔多斯专版2020中考数学复习方案选择填空限时练06试题 9页

选择填空限时练(六)‎ 限时:35分钟　满分:48分 一、选择题(每小题3分,共30分)‎ ‎1.四个实数-2,0,-‎2‎,-1中,最大的实数是(　　)‎ A.-2 B.0‎ C.-‎2‎ D.-1‎ ‎2.某种生物孢子的直径为0.00063 m,这个数据用科学记数法表示为 (　　)‎ A.0.63×10-3 m B.6.3×10-4 m C.6.3×10-3 m D.63×10-5 m ‎3.如图X6-1,在△ABC中,∠A=30°,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E,则下列结论错误的是 (　　)‎ 图X6-1‎ A.DE=DC B.AD=DB C.AD=BC D.BC=AE ‎4.某单位组织职工开展植树活动,植树量与人数之间关系如图X6-2所示,下列说法不正确的是 (　　)‎ 图X6-2‎ A.参加本次植树活动共有30人 B.每人植树量的众数是4棵 C.每人植树量的中位数是5棵 D.每人植树量的平均数是5棵 ‎5.用直尺和圆规作Rt△ABC斜边AB上的高线CD,如图X6-3所示四个作图中,作法错误的是 (　　)‎ 9‎ 图X6-3‎ ‎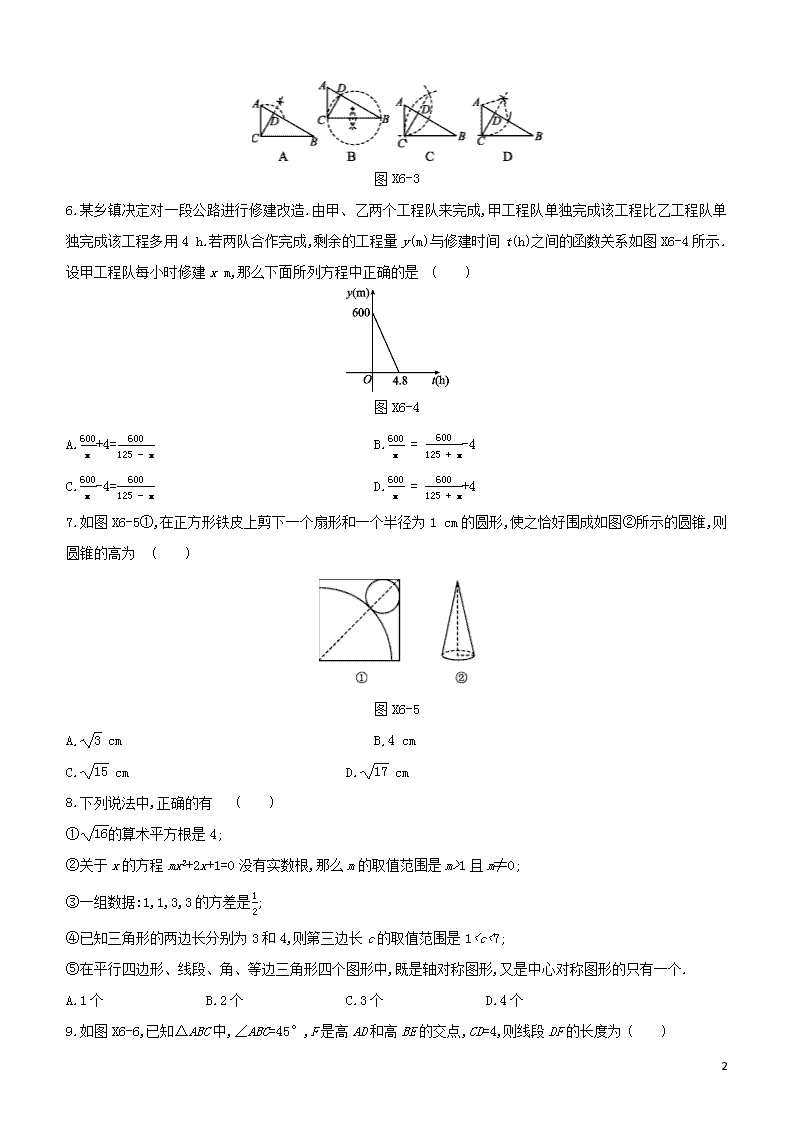6.某乡镇决定对一段公路进行修建改造.由甲、乙两个工程队来完成,甲工程队单独完成该工程比乙工程队单独完成该工程多用4 h.若两队合作完成,剩余的工程量y(m)与修建时间t(h)之间的函数关系如图X6-4所示.设甲工程队每小时修建x m,那么下面所列方程中正确的是 (　　)‎ ‎ 图X6-4 ‎ A.‎600‎x+4=‎600‎‎125-x B.‎600‎x‎=‎‎600‎‎125+x-4‎ C.‎600‎x-4=‎600‎‎125-x D.‎600‎x‎=‎‎600‎‎125+x+4‎ ‎7.如图X6-5①,在正方形铁皮上剪下一个扇形和一个半径为1 cm的圆形,使之恰好围成如图②所示的圆锥,则圆锥的高为 (　　)‎ 图X6-5‎ A.‎3‎ cm B.4 cm C.‎15‎ cm D.‎17‎ cm ‎8.下列说法中,正确的有 (　　)‎ ‎①‎16‎的算术平方根是4;‎ ‎②关于x的方程mx2+2x+1=0没有实数根,那么m的取值范围是m>1且m≠0;‎ ‎③一组数据:1,1,3,3的方差是‎1‎‎2‎;‎ ‎④已知三角形的两边长分别为3和4,则第三边长c的取值范围是1‎ 9‎ ‎0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,则AF·BE=　　　　. ‎ 图X6-10‎ ‎16.如图X6-11,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为　　　　. ‎ 图X6-11‎ 附加训练 ‎ ‎17.解分式方程:‎3‎x-2‎‎-x‎2x-4‎=‎‎1‎‎2‎.‎ ‎18.小李经营一家水果店,某日到水果批发市场批发一种水果,经了解,一次性批发这种水果不得少于100千克,超过300千克时,所有这种水果的批发单价均为3元/千克,图X6-12中折线表示批发单价y(元/千克)与质量x(千克)的函数关系.‎ ‎(1)求图中线段AB所在直线的函数表达式;‎ ‎(2)小李用800元一次可以批发这种水果的质量是多少?‎ 图X6-12‎ 9‎ 基础解答组合限时练(一)‎ 限时:20分钟　满分:20分 ‎17.(8分)(1)计算:(-3)0-‎12‎+|1-‎3‎|-(-1)-2.‎ ‎(2)先化简,再求值:xx-1‎-x÷x-2‎x‎2‎‎-2x+1‎,其中x的值是方程x2-x-2=0的根.‎ ‎18.(4分)解不等式组‎5x-1‎‎6‎‎+2>x+5‎‎4‎,‎‎2x+5≤3(5-x),‎并找出所有整数解.‎ ‎19.(8分)某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.‎ 9‎ 初始位置如图J1-1①,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图②).工作时如图J1-1③,动臂BC会绕点B转动,当点A,B,C在同一直线上时,斗杆顶点D升至最高点(示意图④).‎ ‎(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数;‎ ‎(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?‎ ‎(参考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,‎3‎≈1.73)‎ 图J1-1‎ 9‎ ‎【参考答案】‎ ‎1.B　2.B　3.C　4.D　5.D ‎6.C　[解析]由题意可知两个工程队合作每小时的工作量为600÷4.8=125(m),甲工程队每小时修建x m,所以乙工程队每小时修建(125-x)m,列方程,得‎600‎x-4=‎600‎‎125-x.故选C.‎ ‎7.C ‎8.B　[解析]①‎16‎=4,4的算术平方根是2,故此说法错误;‎ ‎②关于x的方程mx2+2x+1=0没有实数根,那么m的取值范围是m>1,故此说法错误;‎ ‎③平均数是2,方差是‎1‎‎4‎[(1-2)2+(1-2)2+(3-2)2-(3-2)2]=1,故此说法错误;‎ ‎④已知三角形的两边长分别为3和4,则第三边长c的取值范围是1-3　12.k>-1且k≠0　13.‎2‎‎3‎　‎ ‎14.(-‎2‎,0)　15.8‎ ‎16.1或‎9‎‎4‎　[解析]如图①所示,当∠CFE=90°时,△ECF是直角三角形.‎ 由折叠,可得∠PFE=∠A=90°,AE=FE=DE.‎ ‎∴∠CFP=180°,即点P,F,C在一条直线上.‎ 在Rt△CDE和Rt△CFE中,‎CE=CE,‎ED=EF,‎ ‎∴Rt△CDE≌Rt△CFE(HL).∴CF=CD=4.‎ 设AP=FP=x,则BP=4-x,CP=x+4.‎ 在Rt△BCP中,由BP2+BC2=PC2,得 ‎(4-x)2+62=(x+4)2,解得x=‎9‎‎4‎,即AP=‎9‎‎4‎.‎ 如图②所示,当∠CEF=90°时,△ECF是直角三角形,‎ 过点F作FH⊥AB于点H,作FQ⊥AD于点Q,则∠FQE=∠D=90°.‎ 又∵∠FEQ+∠CED=90°=∠ECD+∠CED,‎ ‎∴∠FEQ=∠ECD.∴△FEQ∽△ECD.‎ ‎∴FQED‎=QEDC=‎EFCE,即FQ‎3‎‎=QE‎4‎=‎‎3‎‎5‎.‎ 解得FQ=‎9‎‎5‎,QE=‎12‎‎5‎.‎ ‎∴AQ=HF=‎3‎‎5‎,AH=‎9‎‎5‎.‎ 设AP=FP=x,则HP=‎9‎‎5‎-x.‎ 在Rt△PFH中,HP2+HF2=PF2,‎ 9‎ 即‎9‎‎5‎-x2+‎3‎‎5‎2=x2,‎ 解得x=1,即AP=1.‎ 综上所述,AP的长为1或‎9‎‎4‎.‎ ‎17.解:去分母得:6-x=x-2,解得:x=4,‎ 经检验x=4是分式方程的解.‎ ‎18.解:(1)设直线AB的函数表达式为y=kx+b,由图可得,点A的坐标为(100,5),B的坐标为(300,3),则‎5=100k+b,‎‎3=300k+b,‎解得:‎k=-0.01,‎b=6,‎ ‎∴图中线段AB所在直线的函数表达式为y=-0.01x+6.‎ ‎(2)设批发x kg,∵800<300×3,∴x<300.则单价为(-0.01x+6)元/千克,‎ 根据题意可列方程:(-0.01x+6)x=800,‎ 解得:x1=200,x2=400(舍去),‎ ‎∴小李用800元一次可以批发这种水果200千克.‎ 9‎