中考数学解题指导专题18：动态几何之和差问题探讨 58页

1 【2013 年中考攻略】专题 18：动态几何之和差问题探讨 动态题是近年来中考的的一个热点问题，动态包括点动、线动和面动三大类，解这类题目要“以静制 动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况。常见的题型包括最值问 题、面积问题、和差问题、定值问题和存在性问题等。前面我们已经对最值问题、面积问题进行了探讨， 本专题对和差问题进行探讨。 结合 2011 年和 2012 年全国各地中考的实例，我们从四方面进行动态几何之和差问题的探讨：（1）静 态和差问题；（2）和差为定值问题；（3）和差最大问题；（ 4）和差最小问题。 一、静态和差问题： 典型例题： 例 1：（2012 海南省 3 分）如图，在△ABC 中，∠B 与∠C 的平分线交于点 O. 过 O 点作 DE∥BC，分别交 AB、AC 于 D、E．若 AB=5，AC=4，则△ADE 的周长是 ▲ . 【答案】9。 【考点】角平分线定义，平行线的性质，等腰三角形的判定。 【分析】∵OB 是∠B 的平分线，∴∠DBO=∠OBC。 又∵DE∥BC，∴∠OBC =∠BOD。∴∠DBO=∠BOD。∴DO=DB。 同理，EO=EC。 又∵AB=5，AC=4， ∴△ADE 的周长=AD＋DE＋AE=AD＋DO＋EO＋AE=AD＋DB＋EC＋AE=AB＋AC=5＋4=9。 例 2：（2012 湖北荆门 3 分）如图，已知正方形 ABCD 的对角线长为 2 ，将正方形 ABCD 沿直线 EF 折 叠，则图中阴影部分的周长为【 】 A． 8 B． 4 C． 8 D． 6 2 【答案】C。 【考点】翻折变换（折叠问题），折叠的对称性质，正方形的性质，勾股定理。 【分析】如图，∵正方形 ABCD 的对角线长为 2 2 ，即 BD=2 ，∠A=90°，AB=AD，∠ABD=45°， ∴AB=BD•cos∠ABD=BD•cos45°=2 22 =22 。 ∴AB=BC=CD=AD=2。 由折叠的性质：A′M=AM，D′N=DN，A′D′=AD， ∴图中阴影部分的周长为 A′M+BM+BC+CN+D′N+A′D′=AM+BM+BC+CN+DN+AD=AB+BC+CD+AD=2+2+2+2=8。 故选 C。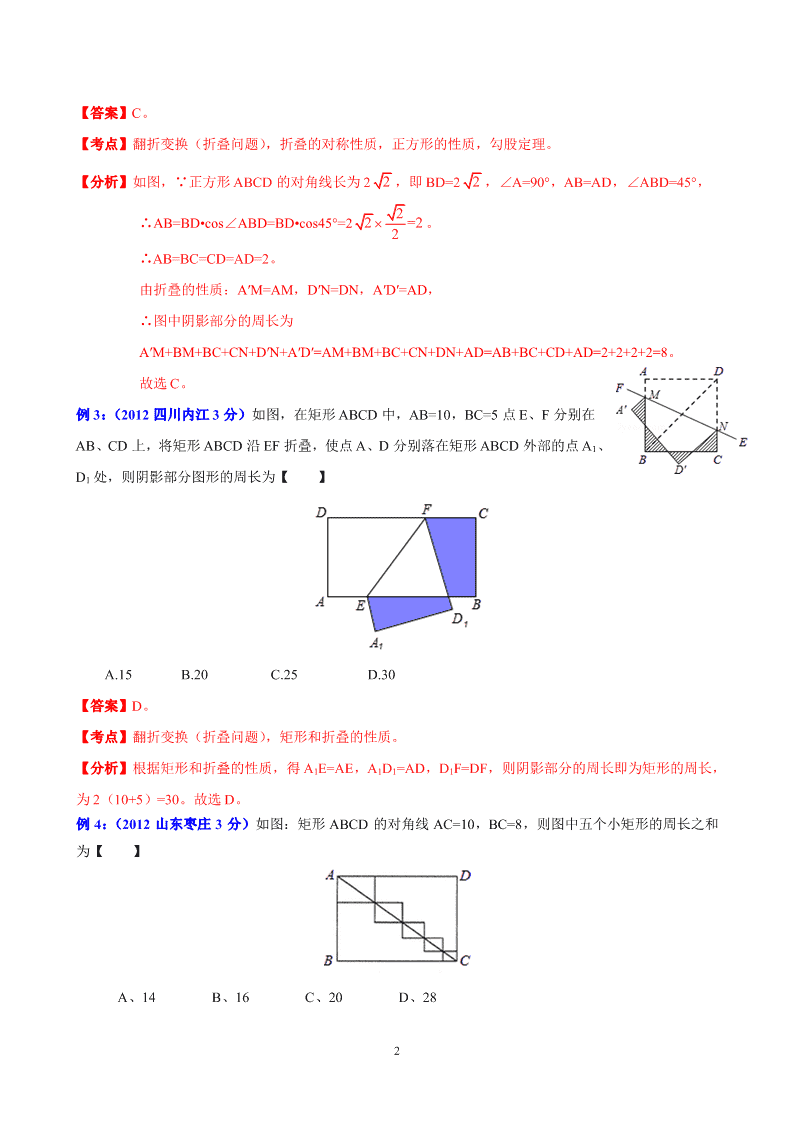 例 3：（2012 四川内江 3 分）如图，在矩形 ABCD 中，AB=10，BC=5 点 E、F 分别在 AB、CD 上，将矩形 ABCD 沿 EF 折叠，使点 A、D 分别落在矩形 ABCD 外部的点 A1、 D1 处，则阴影部分图形的周长为【 】 A.15 B.20 C.25 D.30 【答案】D。 【考点】翻折变换（折叠问题），矩形和折叠的性质。 【分析】根据矩形和折叠的性质，得 A1E=AE，A1D1=AD，D1F=DF，则阴影部分的周长即为矩形的周长， 为 2（10+5）=30。故选 D。 例 4：（2012 山东枣庄 3 分）如图：矩形 ABCD 的对角线 AC=10，BC=8，则图中五个小矩形的周长之和 为【 】 A、14 B、16 C、20 D、28 3 【答案】D。 【考点】平移的性质，勾股定理。 【分析】由勾股定理，得 AB= 2 2 2 2AC BC 10 8 6    ，将五个小矩形的所有上边平移至 AD，所有下 边平移至 BC，所有左边平移至 AB，所有右边平移至 CD， ∴五个小矩形的周长之和=2（AB+CD）=2×（6+8）=28。故选 D。 例 5：（2012 湖北武汉 3 分）在面积为 15 的平行四边形 ABCD 中，过点 A 作 AE 垂直于直线 BC 于点 E， 作 AF 垂直于直线 CD 于点 F，若 AB＝5，BC＝6，则 CE＋CF 的值为【 】 A．11＋11 3 2 B．11－ C．11＋ 或 11－ D．11－ 或1＋ 3 2 【答案】C。 【考点】平行四边形的性质和面积，勾股定理。 【分析】依题意，有如图的两种情况。设 BE=x，DF=y。 如图 1，由 AB＝5，BE=x，得 2 2 2AE AB BE 25 x    。 由平行四边形 ABCD 的面积为 15，BC＝6，得 26 25 x =15 ， 解得 53x= 2 （负数舍去）。 由 BC＝6，DF=y，得 2 2 2AF AD DF 36 y    。 由平行四边形 ABCD 的面积为 15，AB＝5，得 25 36 y =15 ， 解得 y= 3 3 （负数舍去）。 ∴CE＋CF=（6－ 53 2 ）＋（5－33）=11－11 3 2 。 如图 2，同理可得 BE= 53 2 ，DF= 。 ∴CE＋CF=（6＋ ）＋（5＋ ）=11＋ 。 故选 C。 例 6：（2012 山东枣庄 8 分）已知：如图，在四边形 ABCD 中，∠ABC＝90°，CD⊥AD，AD2＋CD2＝2AB2． （1）求证：AB＝BC； （2）当 BE⊥AD 于 E 时，试证明：BE＝AE＋CD． 4 【答案】解：（1）证明：连接 AC。 ∵∠ABC＝90°，∴AB2＋BC2＝AC2。 ∵CD⊥AD，∴AD2＋CD2＝AC2。 ∵AD2＋CD2＝2AB2，∴AB2＋BC2＝2AB2。 ∴AB＝BC。 （2）证明：过 C 作 CF⊥BE 于 F。 ∵BE⊥AD，∴四边形 CDEF 是矩形。∴CD＝EF。 ∵∠ABE＋∠BAE＝90°，∠ABE＋∠CBF＝90°，∴∠BAE＝∠CBF。 又∵AB＝BC，∠BEA＝∠CFB，∴△BAE≌△CBF（AAS）。 ∴AE＝BF。 ∴BE＝BF＋EF ＝AE＋CD。 【考点】勾股定理，矩形的性质，全等三角形的判定和性质。 【分析】（1）题目中存在直角，垂直，含线段平方的等式，因此考虑连接 AC，构造直角三角形，利用勾 股定理证明。 （2）可采用“截长”法证明，过点 C 作 CF⊥BE 于 F，易证 CD=EF，只需再证明 AE=BF 即可，这 一点又可通过全等三角形获证. 例 7：（2012 内蒙古呼和浩特 7 分）如图，四边形 ABCD 是正方形，点 G 是 BC 边上任意一点，DE⊥AG 于 E，BF∥DE，交 AG 于 F． （1）求证：AF﹣BF=EF； （2）将△ABF 绕点 A 逆时针旋转，使得 AB 与 AD 重合，记此时点 F 的对应点为点 F′，若正方形边长为 3，求点 F′与旋转前的图中点 E 之间的距离． 5 【答案】（1）证明：如图，∵正方形 ABCD，∴AB=AD，∠BAD=∠BAG+∠EAD=90°。 ∵DE⊥AG，∴∠AED=90°。∴∠EAD+∠ADE=90°。∴∠ADE=∠BAF。 又∵BF∥DE，∴∠AEB=∠AED=90°。 在△AED 和△BFA 中，∵∠AEB=∠AED，∠ADE=∠BAF，AD = AB。 ∴△AED≌△BDA（AAS）。 ∴BF=AE。 ∵AF﹣AE=EF，∴AF﹣BF=EF。 （2）解：如图， 根据题意知：∠FAF′=90°，DE=AF′=AF， ∴∠F′AE=∠AED=90°，即∠F′AE+∠AED=180°。 ∴AF′∥ED。∴四边形 AEDF′为平行四边形。 又∵∠AED=90°，∴四边形 AEDF′是矩形。 ∴EF′=AD=3。 ∴点 F′与旋转前的图中点 E 之间的距离为 3。 【考点】正方形的性质，旋转的性质，全等三角形的判定和性质，矩形的判定和性质。 【分析】（1）由四边形 ABCD 为正方形，可得出∠BAD 为 90°，AB=AD，进而得到∠BAG 与∠EAD 互余， 又 DE 垂直于 AG，得到∠EAD 与∠ADE 互余，根据同角的余角相等可得出∠ADE=∠BAF，利用 AAS 可 得出三角形 ABF 与三角形 ADE 全等，利用全等三角的对应边相等可得出 BF=AE，由 AF﹣AE=EF，等量 代换可得证。 （2）将△ABF 绕点 A 逆时针旋转，使得 AB 与 AD 重合，记此时点 F 的对应点为点 F′，连接 EF′， 如图所示，由旋转的性质可得出∠FAF′为直角，AF=AF′，由（1）的全等可得出 AF=DE，等量代换可得出 DE=AF′=AF，再利用同旁内角互补两直线平行得到 AF′与 DE 平行，根据一组对边平行且相等的四边形为 平行四边形可得出 AEDF′为平行四边形，再由一个角为直角的平行四边形为矩形可得出 AEDF′为矩形，根 据矩形的对角线相等可得出 EF′=AD，由 AD 的长即可求出 EF′的长。 例 8：（2012 重庆市 10 分）已知：如图，在菱形 ABCD 中，F 为边 BC 的中点，DF 与对角线 AC 交于点 M， 过 M 作 ME⊥CD 于点 E，∠1=∠2． （1）若 CE=1，求 BC 的长； （2）求证：AM=DF+ME． 6 【答案】解：（1）∵四边形 ABCD 是菱形，∴AB∥CD。∴∠1=∠ACD。 ∵∠1=∠2，∴∠ACD=∠2。∴MC=MD。 ∵ME⊥CD，∴CD=2CE。 ∵CE=1，∴CD=2。∴BC=CD=2。 （2）证明：∵F 为边 BC 的中点，∴BF=CF= 1 2 BC。∴CF=CE。 ∵在菱形 ABCD 中，AC 平分∠BCD，∴∠ACB=∠ACD。 在△CEM 和△CFM 中，∵CE=CF，∠ACB=∠ACD，CM=CM， ∴△CEM≌△CFM（SAS）， ∴ME=MF。 延长 AB 交 DF 于点 G， ∵AB∥CD，∴∠G=∠2。 ∵∠1=∠2，∴∠1=∠G。 ∴AM=MG。 在△CDF 和△BGF 中， ∵∠G=∠2，∠BFG=∠CFD，BF=CF，∴△CDF≌△BGF（AAS）。 ∴GF=DF。 由图形可知，GM=GF+MF，∴AM=DF+ME。 【考点】菱形的性质，平行的性质，等腰三角形的判定和性质，全等三角形的判定和性质。 【分析】（1）根据菱形的对边平行可得 AB∥D，再根据两直线平行，内错角相等可得∠1=∠ACD，所以 ∠ACD=∠2，根据等角对等边的性质可得 CM=DM，再根据等腰三角形三线合一的性质可得 CE=DE，然 后求出 CD 的长度，即为菱形的边长 BC 的长度。 （2）先利用 SAS 证明△CEM 和△CFM 全等，根据全等三角形对应边相等可得 ME=MF，延长 AB 交 DF 于点 G，然后证明∠1=∠G，根据等角对等边的性质可得 AM=GM，再利用 AAS 证明△CDF 和 △BGF 全等，根据全等三角形对应边相等可得 GF=DF，最后结合图形 GM=GF+MF 即可得证。 例 9：（2012 湖北天门、仙桃、潜江、江汉油田 3 分）如图，线段 AC=n+1（其中 n 为正整数），点 B 在线 段 AC 上，在线段 AC 同侧作正方形 ABMN 及正方形 BCEF，连接 AM、ME、EA 得到△AME．当 AB=1 7 时，△AME 的面积记为 S1；当 AB=2 时，△AME 的面积记为 S2；当 AB=3 时，△AME 的面积记为 S3；…； 当 AB=n 时，△AME 的面积记为 Sn．当 n≥2 时，Sn﹣Sn﹣1= ▲ ． 例 10：（2012 贵州铜仁 4 分）如图，在△ABC 中，∠ABC 和∠ACB 的平分线交于点 E，过点 E 作 MN∥BC 交 AB 于 M，交 AC 于 N，若 BM+CN=9，则线段 MN 的长为【 】 A．6 B．7 C．8 D．9 【答案】D。 【考点】角平分线的定义，平行线的性质，等腰三角形的判定和性质。 【分析】∵∠ABC、∠ACB 的平分线相交于点 E，∴∠MBE=∠EBC，∠ECN=∠ECB， ∵MN∥BC，∴∠EBC=∠MEB，∠NEC=∠ECB。∴∠MBE=∠MEB，∠NEC=∠ECN。 ∴BM=ME，EN=CN。∴MN=ME+EN，即 MN=BM+CN。 ∵BM+CN=9∴MN=9。故选 D。 8 例 11：（2012 广东梅州 3 分）如图，在折纸活动中，小明制作了一张△ABC 纸片，点 D、E 分别是边 AB、 AC 上，将△ABC 沿着 DE 折叠压平，A 与 A′重合，若∠A=75°，则∠1+∠2=【 】 A．150° B．210° C．105° D．75° 【答案】A。 【考点】翻折变换（折叠问题），三角形内角和定理。 【分析】∵△A′DE 是△ABC 翻折变换而成，∴∠AED=∠A′ED，∠ADE=∠A′DE，∠A=∠A′=75°。 ∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°，∴∠1+∠2=360°﹣2×105°=150°。 故选 A。 例 12：（2012 湖北孝感 3 分）已知∠α 是锐角，∠α 与∠β 互补，∠α 与∠γ 互余，则∠β－∠γ 的值是【 】 A．45º B．60º C．90º D．180º 【答案】C。 【考点】余角和补角、 【分析】根据互余两角之和为 90°，互补两角之和为 180°，结合题意即可得出答案： 由题意得，∠α＋∠β=180°，∠α＋∠γ=90°， 两式相减可得：∠β－∠γ=90°。故选 C。 例 13：（ 2012 湖南长沙 3 分）如图，AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF= ▲ 度． 【答案】360。 【考点】平行线的性质。 【分析】∵AB∥CD，∴∠BAC+∠ACD=180°…①。 ∵CD∥EF，∴∠CEF+∠ECD=180°…②。 ①+②得，∠BAC+∠ACD+∠CEF+∠ECD=180°+180°=360°，即∠BAC+∠ACE+∠CEF=3 60°。 9 练习题： 1. （2012 辽宁本溪 3 分）如图 在直角△ABC 中，∠BAC=90°，AB=8，AC=6，DE 是 AB 边的垂直平分 线，垂足为 D，交边 BC 于点 E，连接 AE，则△ACE 的周长为【 】 A、16 B、15 C、14 D、13 2. （2012 吉林省 3 分）如图，在等边△ABC 中，D 是边 AC 上一点，连接 BD．将△BCD 绕点 B 逆时 针旋转 60°得到△BAE，连接 ED．若 BC=10，BD=9，则△AED 的周长是_ ▲____. 3. （2012 福建龙岩 3 分）如图，Rt△ABC 中，∠C=90°，AC = BC = 6，E 是斜边 AB 上任意一点，作 EF⊥AC 于 F，EG⊥BC 于 G，则矩形 CFEG 的周长是 ▲ ． 4. （2012 福建宁德 4 分）如图，在矩形 ABCD 中，AB＝2，BC＝3，点 E、F、G、H 分别在矩形 ABCD 的各边上，EF∥HG，EH∥FG，则四边形 EFGH 的周长是【 】 A． 10 B． 13 C．2 10 D．2 13 5. （2012 内蒙古包头 10 分）如图，已知 AB 为⊙O 的直径，过⊙O 上的点 C 的切线交 AB 的延长线于点 E , AD⊥EC 于点 D 且交⊙O 于点 F ，连接 BC , CF , AC 。 （1）求证：BC=CF； 10 （2）若 AD=6 , DE=8 ，求 BE 的长； （3）求证：AF + 2DF = AB。 6. （2012 山东东营 10 分） （1）如图 1，在正方形 ABCD 中，E 是 AB 上一点，F 是 AD 延长线上一点，且 DF＝BE．求证：CE＝CF； （2）如图 2，在正方形 ABCD 中，E 是 AB 上一点，G 是 AD 上一点，如果∠GCE＝45°，请你利用（1） 的结论证明：GE＝BE＋GD． （3）运用（1）（ 2）解答中所积累的经验和知识，完成下题： 如图 3，在直角梯形 ABCD 中，AD∥BC（BC＞AD）， ∠B＝90°，AB＝BC，E 是 AB 上一点，且∠DCE ＝45°，BE＝4，DE=10, 求直角梯形 ABCD 的面积． 7. （2012黑龙江牡丹江8分）如图①，△ABC中。AB=AC，P 为底边BC上一点，PE⊥AB，PF⊥AC， CH⊥AB， 垂足分别为 E、F、H．易证 PE+PF=CH．证明过程如下： 11 （1）如图②，P 为 BC 延长线上的点时，其它条件不变，PE、PF、CH 又有怎样的数量网]关系?请写出你的 猜想，并加以证明： （2）填空：若∠A=300，△ABC 的面积为 49，点 P 在直线 BC上，且 P 到直线 AC 的距离为 PF，当 PF=3 时，则 AB 边上的高 CH= ．点 P 到 AB 边的距离 PE= 8. （2012 江苏南通 3 分）如图，在△ABC 中，∠C＝70º，沿图中虚线截去∠C，则∠1＋∠2＝【 】 A．360º B．250º C．180º D．140º 9.（2012 江苏南京 2 分）如图， 1 、 2 、 3 、 4 是五边形 ABCDE 的 4 个外角，若 2A 10  ，则 1 2 3 4     ▲ 12 10.（2012 四川绵阳 3 分）如图，将等腰直角三角形虚线剪去顶角后，∠1+∠2=【 】。 A．225° B．235° C．270° D．与虚线的位置有关 11.（2012 四川凉山 4 分）如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β 的度数是【 】 A．180 B． 220 C． 240 D．300 二、和差为定值问题： 典型例题： 例 1： （2012 广西崇左 10 分）如图所示，在正方形 ABCD 中，点 E、F 分别在 BC、CD 上移动，但点 A 到 EF 的距离 AH 始终保持与 AB 的长度相等，问在点 E、F 移动过程中； （1）∠EAF 的大小是否发生变化？请说明理由. （2）△ECF 的周长是否发生变化？请说明理由. 【答案】解：（1）∠EAF 的大小不会发生变化。理由如下： 在正方形 ABCD 中，∵AH⊥EF，∴∠AHF=∠D=90°， 13 ∵AF=AF，AH=AD，∴Rt△AHF≌Rt△ADF(HL)。∴∠HAF=∠DAF。 同理 Rt△AHE≌Rt△ABE，∠HAE=∠BAE。 ∵∠HAF+∠DAF+∠HAE+∠BAE=90°，∴∠EAF=∠HAF+∠HAE=45°。 ∴∠EAF 的大小不会发生变化。 （2）△ECF 的周长不会发生变化。理由如下： 由（1）知：Rt△AHF≌Rt△ADF， Rt△AHE≌Rt△ABE， ∴FH=FD，EH=EB。∴EF=EH+FH=EB+FD。 ∴CE+CF+EF= CE+CF+ EB+FD=BC+CD。 ∴CE+CF+EF= CE+CF+ EB+FD=BC+CD。 【考点】正方形的性质，动点和定值问题，全等三角形的判定和性质。 【分析】（1）由 HL 证得 Rt△AHF≌Rt△ADF 和 Rt△AHE≌Rt△ABE 即可得∠EAF=∠HAF+∠HAE=45°， 即∠EAF 的大小不会发生变化。 （2）由（1）两个全等即可得 CE+CF+EF= CE+CF+ EB+FD=BC+CD，即 CE+CF+EF= CE+CF+ EB+FD=BC+CD。 【点评】第二问，△ECF 的周长即 CE+CF+EF 为定值：正方形 ABCD 边长的 2 倍。 例 2：（2012 山东德州 12 分）如图所示，现有一张边长为 4 的正方形纸片 ABCD，点 P 为正方形 AD 边上 的一点（不与点 A、点 D 重合）将正方形纸片折叠，使点 B 落在 P 处，点 C 落在 G 处，PG 交 DC 于 H， 折痕为 EF，连接 BP、BH． （1）求证：∠APB=∠BPH； （2）当点 P 在边 AD 上移动时，△PDH 的周长是否发生变化？并证明你的结论； （3）设 AP 为 x，四边形 EFGP 的面积为 S，求出 S 与 x 的函数关系式，试问 S 是否存在最小值？若存在， 求出这个最小值；若不存在，请说明理由． 【答案】解：（1）如图 1，∵PE=BE，∴∠EBP=∠EPB． 又∵∠EPH=∠EBC=90°， 14 ∴∠EPH﹣∠EPB=∠EBC﹣∠EBP，即∠PBC=∠BPH。 又∵AD∥BC，∴∠APB=∠PBC。∴∠APB=∠BPH。 （2）△PHD 的周长不变为定值 8。证明如下： 如图 2，过 B 作 BQ⊥PH，垂足为 Q。 由（1）知∠APB=∠BPH， 又∵∠A=∠BQP=90°，BP=BP， ∴△ABP≌△QBP（AAS）。 ∴AP=QP，AB=BQ。 又∵AB=BC，∴BC=BQ。 又∵∠C=∠BQH=90°，BH=BH， ∴△BCH≌△BQH（HL）。 ∴CH=QH。 ∴△PHD 的周长为： PD+DH+PH=AP+PD+DH+HC=AD+CD=8。 （3）如图 3，过 F 作 FM⊥AB，垂足为 M，则 FM=BC=AB。 又∵EF 为折痕，∴EF⊥BP。 ∴∠EFM+∠MEF=∠ABP+∠BEF=90°。 ∴∠EFM=∠ABP。 又∵∠A=∠EMF=90°，AB=ME， ∴△EFM≌△BPA（ASA）。 ∴EM=AP=x． ∴在 Rt△APE 中，（4﹣BE）2+x2=BE2，即 2xBE 2+ 8 。 ∴ 2xCF BE EM 2+ x8    。 又∵四边形 PEFG 与四边形 BEFC 全等， ∴     2 221 1 x 1 1S BE CF BC= 4+ x 4= x 2x+8= x 2 +62 2 4 2 2          。 ∵ 1042<<，∴当 x=2 时，S 有最小值 6。 【考点】翻折变换（折叠问题），正方形的性质，折叠的性质，全等三角形的判定和性质，勾股定理，二 次函数的最值。 【分析】（1）根据翻折变换的性质得出∠PBC=∠BPH，进而利用平行线的性质得出∠APB=∠PBC 即可得 出答案。 15 （2）先由 AAS 证明△ABP≌△QBP，从而由 HL 得出△BCH≌△BQH，即可得 CH=QH。因此， △PDH 的周长=PD+DH+PH=AP+PD+DH+HC=AD+CD=8 为定值。 （3）利用已知得出△EFM≌△BPA，从而利用在 Rt△APE 中，（4﹣BE）2+x2=BE2，利用二次函数 的最值求出即可。 例 3：（2012 黑龙江绥化 8 分）如图，点 E 是矩形 ABCD 的对角线 BD 上的一点，且 BE=BC，AB=3，BC=4， 点 P 为直线 EC 上的一点，且 PQ⊥BC 于点 Q，PR⊥BD 于点 R． （1）如图 1，当点 P 为线段 EC 中点时，易证：PR+PQ= 5 12 （不需证明）． （2）如图 2，当点 P 为线段 EC 上的任意一点（不与点 E、点 C 重合）时，其它条件不变，则（1）中的 结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由． （3）如图 3，当点 P 为线段 EC 延长线上的任意一点时，其它条件不变，则 PR 与 PQ 之间又具有怎样的 数量关系？请直接写出你的猜想． 【答案】解：（2）图 2 中结论 PR＋PQ=12 5 仍成立。证明如下： 连接 BP，过 C 点作 CK⊥BD 于点 K。 ∵四边形 ABCD 为矩形，∴∠BCD=90°。 又∵CD=AB=3，BC=4，∴ 2 2 2 2BD CD BC 3 4 5     。 ∵S△BCD= 1 2 BC•CD= BD•CK，∴3×4=5CK，∴CK= 。 ∵S△BCE= BE•CK，S△BEP= PR•BE，S△BCP= PQ•BC，且 S△BCE=S△BEP＋S△BCP， ∴ BE•CK= PR•BE＋ PQ•BC。 又∵BE=BC，∴ CK= PR＋ PQ。∴CK=PR＋PQ。 又∵CK= ，∴PR＋PQ= 。 16 （3）图 3 中的结论是 PR－PQ=12 5 ． 【考点】矩形的性质，三角形的面积，勾股定理。 【分析】（2）连接 BP，过 C 点作 CK⊥BD 于点 K．根据矩形的性质及勾股定理 求出 BD 的长，根据三角形面积相等可求出 CK 的长，最后通过等量代换即可证 明。 （3）图 3 中的结论是 PR－PQ=125 。 连接 BP，S△BPE－S△BCP=S△BEC，S△BEC 是固定值，BE=BC 为两个 底，PR，PQ 分别为高，从而 PR－PQ= 。 例 4：（2012 山东潍坊 11 分）如图，已知抛物线与坐标轴分别交于 A(－2，O)、B(2，0)、C(0，－l)三点， 过坐标原点 O 的直线 y=kx 与抛物线交于 M、N 两点．分别过点 C、D(0，－ 2)作平行于 x 轴的直线 1l 、 2l ． (1)求抛物线对应二次函数的解析式； (2)求证以 ON 为直径的圆与直线 相切； (3)求线段 MN 的长(用 k 表示)，并证明 M、N 两点到直线 的距离之和等于线段 MN 的长． 【答案】解：（1）设抛物线对应二次函数的解析式为 y=ax2＋bx＋c， 则 4a 2b+c=0 4a+2b+c=0 c= 1     解得 1a= 4 b=0 c= 1        。 ∴抛物线对应二次函数的解析式 所以 21y= x 14  。 （2）设 M(x1，y1)，N(x2，y2)，因为点 M、N 在抛物线上， ∴ 22 1 1 2 2 11y = x 1 y = x 144， ，∴x2 2=4(y2+1)。 17 又∵    22 2 2 2 2 2 2 2 2ON x y 4 y 1 y y 2       ，∴ 2ON y 2。 又∵y2≥－l，∴ON=2＋y2。 设 ON 的中点 E，分别过点 N、E 向直线 1l 作垂线，垂 足为 P、F， 则 22yOC NPEF 22 ， ∴ON=2EF， 即 ON 的中点到直线 的距离等于 ON 长度的一半， ∴以 ON 为直径的圆与 相切。 （3）过点 M 作 MH⊥NP 交 NP 于点 H，则    222 2 2 2 1 2 1MN MH NH x x y y      ， 又∵y1=kx1，y2=kx2，∴（y2－y1)2=k2(x2－x1)2。∴MN2=(1+k2)(x2 一 xl)2。 又∵点 M、N 既在 y=kx 的图象上又在抛物线上， ∴ 21kx= x 14  ，即 x2－4kx－4=0，∴x2＋x1=4k，x2·x 1=－4。 ∴MN2=(1+k2)(x2 一 xl)2=(1+k2)[ (x2＋xl)2－4x2·x l] =16(1+k2)2。∴MN=4(1+k2)。 延长 NP 交 2l 于点 Q，过点 M 作 MS⊥ 交 于点 S， 则 MS＋NQ=y1＋2＋y2＋2= 22 12 11x 1+ x 1+444        22 2 2 2 2 1 2 1 2 1 2 1 1 1= x +x +2= x +x 2x x +2= 16k +8 +2=4k +4=4 1+k4 4 4  ∴MS+NQ=MN，即 M、N 两点到 距离之和等于线段 MN 的长。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，中点坐标的求法，直线与圆相切 的条件，一元二次方程根与系数的关系，勾股定理。 【分析】（1）根据点在曲线上，点的坐标满足方程的关系，用待定系数法即可求出抛物线对应二次函数的 解析式。 （2）要证以 ON 为直径的圆与直线 1l 相切，只要证 ON 的中点到直线 的距离等于 ON 长的一半 即可。 （3）运用一元二次方程根与系数的关系，求出 MN 和 M、N 两点到直线 2l 的距离之和，相比较即 可。 例 5：（2012 江苏苏州 9 分）如图，正方形 ABCD 的边 AD 与矩形 EFGH 的边 FG 重合，将正方形 ABCD 18 以 1cm/s 的速度沿 FG 方向移动，移动开始前点 A 与点 F 重合.在移动过程中，边 AD 始终与边 FG 重合， 连接 CG，过点 A 作 CG 的平行线交线段 GH 于点 P，连接 PD.已知正方形 ABCD 的边长为 1cm，矩形 EFGH 的边 FG、GH 的长分别为 4cm、3cm.设正方形移动时间为 x（s），线段 GP 的长为 y（cm），其中 0≤x≤2.5. ⑴试求出 y 关于 x 的函数关系式，并求出 y =3 时相应 x 的值； ⑵记△DGP 的面积为 S1，△CDG 的面积为 S2．试说明 S1－S2 是常数； ⑶当线段 PD 所在直线与正方形 ABCD 的对角线 AC 垂直时，求线段 PD 的长. 【答案】解：（1）∵CG∥AP，∴∠CGD=∠PAG，则 tan CGD=tan PAG。∴ CD PG=GD AG 。 ∵GF=4，CD=DA=1，AF=x，∴GD=3－x，AG=4－x。 ∴ 1y=3 x 4 x ，即 4xy= 3x   。∴y 关于 x 的函数关系式为 。 当 y =3 时， 4x3= 3x   ，解得:x=2.5。 （2）∵    12 1 1 4 x 1 1 1 1 3S = GP GD= 3 x x+2 S = GD CD= 3 x 1 x+2 2 3 x 2 2 2 2 2               ， ， ∴ 12 1 1 3 1S S = x+2 x+2 2 2 2               为常数。 （3）延长 PD 交 AC 于点 Q. ∵正方形 ABCD 中，AC 为对角线，∴∠CAD=45°。 ∵PQ⊥AC，∴∠ADQ=45°。 ∴∠GDP=∠ADQ=45°。 ∴△DGP 是等腰直角三角形，则 GD=GP。 ∴ 4x3 x= 3x   ，化简得： 2x 5x+5=0 ，解得： 55x= 2  。 ∵0≤x≤2.5，∴ 55x= 2  。 19 在 Rt△DGP 中，  0 GD 5 5 2+ 10PD= = 2 3 x = 2 3 =22cos45  。 【考点】正方形的性质，一元二次方程的应用，等腰直角三角形的性质，矩形的性质，解直角三角形，锐 角三角函数定义，特殊角的三角函数值。 【分析】（1）根据题意表示出 AG、GD 的长度，再由 tan CGD=tan PAG可解出 x 的值。 （2）利用（1）得出的 y 与 x 的关系式表示出 S1、S2，然后作差即可。 （3）延长 PD 交 AC 于点 Q，然后判断△ DGP 是等腰直角三角形，从而结合 x 的范围得出 x 的 值，在 Rt△DGP 中，解直角三角形可得出 PD 的长度。 练习题： 1. （广东广州 14 分）已知关于 x 的二次函数  2 0y ax bx c a  ＝ 的图象经过点 C（0，1），且与 轴交 于不同的两点 A、B，点 A 的坐标是（1，0） （1）求 c 的值； （2）求 a 的取值范围； （3）该二次函数的图象与直线 y ＝1 交于 C、D 两点，设 A、B、C、D 四点构成的四边形的对角线相交于 点 P，记△PCD 的面积为 S1，△PAB 的面积为 S2，当 0＜ ＜1 时，求证：S1﹣S2 为常数，并求出该常数． 2. （2011 湖南岳阳 8 分）如图①，将菱形纸片 AB（E）CD（F）沿对角线 BD（EF）剪开，得到△ABD 和△ECF，固定△ABD，并把△ABD 与△ECF 叠放在一起． （1）操作：如图②，将△ECF 的顶点 F 固定在△ABD 的 BD 边上的中点处，△ECF 绕点 F 在 BD 边上方 左右旋转，设旋转时 FC 交 BA 于点 H（H 点不与 B 点重合），FE 交 DA 于点 G（G 点不与 D 点重合）． 求证：BH•GD=BF2 （2）操作：如图③，△ECF 的顶点 F 在△ABD 的 BD 边上滑动（F 点不与 B、D 点重合），且 CF 始终经 过点 A，过点 A 作 AG∥CE，交 FE 于点 G，连接 DG． 探究：FD+DG= ．请予证明． 20 3. （2011 福建莆田 10 分） 如图，将—矩形 OABC 放在直角坐际系中，O 为坐标原点．点 A 在 x 轴正半 轴上．点 E 是边 AB 上的—个动点(不与点 A、N 重合)，过点 E 的反比例函数 ( 0)kyxx的图象与边 BC 交于点 F。 （1）(4 分)若△OAE、△OCF 的而积分别为 S1、S2．且 S1＋S2=2，求 k 的值： （2）(6 分) 若 OA=2．0C=4．问当点 E 运动到什么位置时，四边形 OAEF 的面积最大．其最大值为多少? 4. （2011 黑龙江龙东五市 8 分）如图，点 E 是矩形 ABCD 的对角线 BD 上的一点，且 BE=BC，AB=3， BC=4，点 P 为直线 EC 上的一点，且 PQ⊥BC 于点 Q，PR⊥BD 于点 R。 （1）如图 1，当点 P 为线段 EC 中点时，易证：PR+PQ= 5 12 （不需证明）。 （2）如图 2，当点 P 为线段 EC 上的任意一点（不与点 E、点 C 重合）时，其它条件不变，则（1）中 的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由。 （3）如图 3，当点 P 为线段 EC 延长线上的任意一点时，其它条件不变，则 PR 与 PQ 之间又具有怎样 的数量关系？请直接写出你的猜想。 5. （2011 湖南永州 10 分）探究问题： ⑴方法感悟：如图①，在正方形 ABCD 中，点 E，F 分别为 DC，BC 边上的点，且满足∠EAF=45°，连接 EF，求证 DE+BF=EF． 感悟解题方法，并完成下列填空： 将△ADE 绕点 A 顺时针旋转 90°得到△ABG，此时 AB 与 AD 重合，由旋转可得： AB=AD，BG=DE, ∠1=∠2，∠ABG=∠D=90°，∴∠ABG+∠ABF=90°＋90°=180°， 21 因此，点 G，B，F 在同一条直线上． ∵∠EAF=45° ∴∠2＋∠3=∠BAD－∠EAF=90°－45°=45°． ∵∠1=∠2， ∴∠1＋∠3=45°．即∠GAF=∠_________． 又 AG=AE，AF=AF∴△GAF≌_______．∴_________=EF，故 DE＋BF=EF． ⑵方法迁移： 如图②，将 Rt△ABC 沿斜边翻折得到△ADC，点 E，F 分别为 DC，BC 边上的点，且∠EAF= 2 1 ∠DAB．试 猜想 DE，BF，EF 之间有何数量关系，并证明你的猜想． ⑶问题拓展： 如图③，在四边形 ABCD 中，AB=AD，E，F 分别为 DC,BC 上的点，满足∠EAF= ∠DAB,试猜想当∠B 与∠D 满足什么关系时，可使得 DE+BF=EF．请直接写出你的猜想（不必说明理由）． 6.（2011 福建莆田 14 分）已知菱形 ABCD 的边长为 1．∠ADC=60°，等边△AEF 两边分别交边 DC、CB 于点 E、F。 （1）（ 4 分）特殊发现：如图 1，若点 E、F 分别是边 DC、CB 的中点．求证：菱形 ABCD 对角线 AC、 BD 交点 O 即为等边△AEF 的外心； （2）若点 E、F 始终分别在边 DC、CB 上移动．记等边△AEF 的外心为点 P． ①（4 分）猜想验证：如图 2．猜想△AEF 的外心 P 落在哪一直线上，并加以证明； ②（6 分）拓展运用：如图 3，当△AEF 面积最小时，过点 P 任作一直线分别交边 DA 于点 M，交边 DC 的延长线于点 N，试判断 11 DM DN 是否为定值．若是．请求出该定值；若不是．请说明理由。 22 三、和差最大问题： 典型例题： 例 1： （2012 广西崇左 10 分）如图所示，抛物线 cbxaxy  2 （a≠0）的顶点坐标为点 A（－2，3）， 且抛物线 与 y 轴交于点 B（0，2）. （1）求该抛物线的解析式； （2）是否在 x 轴上存在点 P 使△PAB 为等腰三角形，若存在，请求出点 P 的坐标；若不存在，请说 明理由； （3）若点 P 是 x 轴上任意一点，则当 PA－PB 最大时，求点 P 的坐标. 【答案】解：（1）∵抛物线的顶点坐标为 A(－2，3)，∴可设抛物线的解析式为 2y a(x 2) 3   。 由题意得 2a(0 2) 3 2   ，解得 1a 4 。 ∴物线的解析式为 21y (x 2) 34    ，即 21y x x 24    。 （2）设存在符合条件的点 P，其坐标为（p，0），则 PA 2 = 22( 2 p) 3   ，PB= 22p2 ，AB = 22(3 2) 2 5   当 PA=PB 时， = ，解得 9p 4 ； 当 PA=PB 时， =5，方程无实数解； 当 PB=AB 时， =5，解得 p1 。 ∴x 轴上存在符合条件的点 P，其坐标为（ 9 4 ，0）或（-1,0）或（1,0）。 （3）∵PA－PB≤AB，∴当 A、B、P 三点共线时，可得 PA－PB 的最大值，这个最大值等于 AB， 此时点 P 是直线 AB 与 x 轴的交点。 设直线 AB 的解析式为 y=kx+b，则 23 b2 2k b 3     ，解得 1k 2 b2     。∴直线 AB 的解析式为 1y x 22   ， 当 =0 时，解得 x4 。 ∴当 PA－PB 最大时，点 P 的坐标是（4，0）。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，等腰三角形的判定和性质。 【分析】（1）由已知用待定系数法，设顶点式求解。 （2）分 PA=PB、PA=PB、PB=A 三种情况讨论即可。 （3）求得 PA－PB 最大时的位置，即可求解。 例 3：（2012 广东广州 14 分）如图，在平行四边形 ABCD 中，AB=5，BC=10，F 为 AD 的中点，CE⊥AB 于 E，设∠ABC=α（60°≤α＜90°）． （1）当 α=60°时，求 CE 的长； （2）当 60°＜α＜90°时， ①是否存在正整数 k，使得∠EFD=k∠AEF？若存在，求出 k 的值；若不存在，请说明理由． 24 ②连接 CF，当 CE2﹣CF2 取最大值时，求 tan∠DCF 的值． 【答案】解：（1）∵α=60°，BC=10，∴sinα= CE BC ，即 sin60°= CE 3 10 2 ，解得 CE=53。 （2）①存在 k=3，使得∠EFD=k∠AEF。理由如下： 连接 CF 并延长交 BA 的延长线于点 G， ∵F 为 AD 的中点，∴AF=FD。 在平行四边形 ABCD 中，AB∥CD，∴∠G=∠DCF。 在△AFG 和△CFD 中， ∵∠G=∠DCF， ∠G=∠DCF，AF=FD， ∴△AFG≌△CFD（AAS）。 ∴CF=GF，AG=CD。 ∵CE⊥AB，∴EF=GF。∴∠AEF=∠G。 ∵AB=5，BC=10，点 F 是 AD 的中点，∴AG=5，AF= 1 2 AD= BC=5。∴AG=AF。 ∴∠AFG=∠G。 在△AFG 中，∠EFC=∠AEF+∠G=2∠AEF， 又∵∠CFD=∠AFG，∴∠CFD=∠AEF。 ∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF， 因此，存在正整数 k=3，使得∠EFD=3∠AEF。 ②设 BE=x，∵AG=CD=AB=5，∴EG=AE+AG=5﹣x+5=10﹣x， 在 Rt△BCE 中，CE2=BC2﹣BE2=100﹣x2。 在 Rt△CEG 中，CG2=EG2+CE2=（10﹣x）2+100﹣x2=200﹣20x。 ∵CF=GF（①中已证），∴CF2=（ CG）2= 1 4 CG2= （200﹣20x）=50﹣5x。 ∴CE2﹣CF2=100﹣x2﹣50+5x=﹣x2+5x+50=﹣（x﹣ 5 2 ）2+50+ 25 4 。 ∴当 x= ，即点 E 是 AB 的中点时，CE2﹣CF2 取最大值。 此时，EG=10﹣x=10﹣ 5 15=22 ，CE= 2 25 5 15100 x = 100 =42 ， 25 ∴ 5 15 CG 152tan DCF tan G 15EG 3 2       。 【考点】锐角三角函数定义，特殊角的三角函数值，平行四边形的性质，对顶角的性质，全等三角形的判 定和性质，直角三角形斜边上的中线性质，等腰三角形的性质，二次函数的最值，勾股定理。 【分析】（1）利用 60°角的正弦值列式计算即可得解。 （2）①连接 CF 并延长交 BA 的延长线于点 G，利用“角边角”证明△AFG 和△CFD 全等，根据全 等三角形对应边相等可得 CF=GF，AG=CD，再利用直角三角形斜边上的中线等于斜边的一半可得 EF=GF， 再根据 AB、BC 的长度可得 AG=AF，然后利用等边对等角的性质可得∠AEF=∠G=∠AFG，根据三角形 的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G，然后推出∠EFD=3∠AEF，从而得解。 ②设 BE=x，在 Rt△BCE 中，利用勾股定理表示出 CE2，表示出 EG 的长度，在 Rt△CEG 中， 利用勾股定理表示出 CG2，从而得到 CF2，然后相减并整理，再根据二次函数的最值问题解答。 例 4：（2012 河北省 12 分）如图 1 和 2，在△ABC 中，AB=13，BC=14，cos∠ABC= 5 13 ． 探究：如图 1，AH⊥BC 于点 H，则 AH= ，AC= ，△ABC 的面积 S△ABC= ； 拓展：如图 2，点 D 在 AC 上（可与点 A，C 重合），分别过点 A、C 作直线 BD 的垂线，垂足为 E，F， 设 BD=x，AE=m，CF=n（当点 D 与点 A 重合时，我们认为 S△ABD=0） （1）用含 x，m，n 的代数式表示 S△ABD 及 S△CBD； （2）求（m+n）与 x 的函数关系式，并求（m+n）的最大值和最小值； （3）对给定的一个 x 值，有时只能确定唯一的点 D，指出这样的 x 的取值范围． 发现：请你确定一条直线，使得 A、B、C 三点到这条直线的距离之和最小（不必写出过程），并写出这个 最小值． 【答案】解：探究：12；15；84。 拓展：（1）由三角形面积公式，得 26 ABD 11S BD AE xm22    ， CBD 11S BD CF xn22    。 （2）由（1）得 ABD2Sm x  ， CBD2Sn x  ， ∴ CBD ABCABD 2S 2S2S 168m+n +x x x x    ∵△ABC 中 AC 边上的高为 ABC2S 168 56==AC 15 5  ， ∴x 的取值范围为 56 x 145  。 ∵ m+n 随 x 的增大而减小， ∴当 56x= 5 时， 的最大值为 15，当 x=14 时， 的最小值为 12。 （3）x 的取值范围为 或13 x 14<  。 发现：直线 AC，A、B、C 三点到这条直线的距离之和最小，最小值为 56 5 。 【考点】动点问题，锐角三角函数定义，特殊角有三角函数值，勾股定理， 垂直线段的性质，反比例函 数的性质。 【分析】探究：在 Rt△ABH 中，AB=13， 5cos ABC 13，∴BH=AB 5cos ABC 13 513     。 ∴根据勾股定理，得 2 2 2 2AH AB BH 13 5 12     。 ∵BC=14，∴HC=BC－BH=9。∴根据勾股定理，得 2 2 2 2AC AB +HC 12 +9 15   。 ∴ ABC 11S BC AH 14 12 8422       。 拓展：（1）直接由三角形面积公式可得。 （2）由（1）和 ABC ABD CBDS S +S   即可得到 关于 x 的反比例函数关系式。根据垂 直线段最短的性质，当 BD⊥AC 时，x 最小，由面积公式可求得；因为 AB=13，BC=14，所以当 BD=BC=14 时，x 最大。从而根据反比例函数的性质求出 m+n）的最大值和最小值。 （3）当 时，此时 BD⊥AC，在线段 AC 上存在唯一的点 D；当 56 x 135 <  时，此 时在线段 AC 上存在两点 D；当 时，此时在线段 AC 上存在唯一的点 D。因此 x 的取值范围为 或 。 发现：由拓展（2）知，直线 AC，A、B、C 三点到这条直线的距离之和（即△ABC 中 AC 边上的 高）最小，最小值为 （它小于 BC 边上的高 12 和 AB 边上的高 ABC2S 168=AB 13  ）。 27 练习题： 1. （2011 内蒙古乌兰察布 4 分）如图，BE 是半径为 6 的⊙D 的 4 1 圆周，C 点是 上的任意一点， △ABD 是等边三角形,则四边形 ABCD 的周长 P 的取值范围是 ▲ 2.（2011 四川广安 12 分）如图所示，在平面直角坐标系中，四边形 ABCD 是直角梯形，BC∥AD，∠BAD=90°， BC 与 y 轴相交于点 M，且 M 是 BC 的中点，A、B、D 三点的坐标分别是 A（ 1 0 ， ）， B（ 1 2 ， ）， D（3，0）．连接 DM，并把线段 DM 沿 DA 方向平移到 ON．若抛物线 2y ax bx c   经过点 D、M、N． （1）求抛物线的解析式． （2）抛物线上是否存在点 P，使得 PA=PC，若存在，求出点 P 的坐标；若不存在，请说明理由． （3）设抛物线与 x 轴的另一个交点为 E，点 Q 是抛物线的对称轴上的一个动点，当点 Q 在什么位置时有 |QE-QC|最大？并求出最大值． 3. （2011 河南省 11 分）如图，在平面直角坐标系中，直线 33 42yx与抛物线 21 4y x bx c    交于 A、B 两点，点 A 在 x 轴上，点 B 的横坐标为﹣8． （1）求该抛物线的解析式； （2）点 P 是直线 AB 上方的抛物线上一动点（不与点 A、B 重合），过点 P 作 x 轴的垂线，垂足为 C，交 直线 AB 于点 D，作 PE⊥AB 于点 E． ①设△PDE 的周长为l ，点 P 的横坐标为 x ，求l 关于 x 的函数关系式，并求出l 的最大值； ②连接 PA，以 PA 为边作图示一侧的正方形 APFG．随着点 P 的运动，正方形的大小、位置也随之改变．当 顶点 F 或 G 恰好落在 y 轴上时，直接写出对应的点 P 的坐标． 28 4. （2011 山东青岛 10 分）)问题提出：我们在分析解决某些数学问题时，经常要比较两个数或代数式的大 小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是 通过作差、变形，并利用差的符号确定他们的大小，即要比较代数式 M、N 的大小，只要作出它们的差 M －N，若 M－N＞0，则 M＞N；若 M－N＝0，则 M＝N；若 M－N＜0，则 M＜N． 问题解决：如图 1，把边长为 a ＋b( ≠b)的大正方形分割成两个边长分别是 、b 的小正方形 及两个矩形，试比较两个小正方形面积之和 M 与两个矩形面积之和 N 的大小． 解：由图可知：M＝ 2＋ b 2，N＝2 ．∴M－N＝ 2＋ 2－2 ＝( － )2． ∵ ≠ ，∴( － )2＞0．∴M－N＞0．∴M＞N． 类别应用：(1)已知小丽和小颖购买同一种商品的平均价格分别为 2 ab 元/千克和 2ab ab 元/千克 ( 、 是正数，且 ≠ )，试比较小丽和小颖所购买商品的平均价格的高低． (2)试比较图 2 和图 3 中两个矩形周长 M1、N1 的大小( ＞ c )． 联系拓广：小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图 4 所示(其中 b＞a＞c＞0)，售货员分别可按图 5、图 6、图 7 三种方法进行捆绑，问哪种方法用绳最短？哪 种方法用绳最长？请说明理由． 29 四、和差最小问题： 典型例题： 例 1：（2012 浙江台州 4 分）如图，菱形 ABCD 中，AB=2，∠A=120°，点 P，Q，K 分别为线段 BC，CD， BD 上的任意一点，则 PK+QK 的最小值为【 】 A． 1 B． 3 C． 2 D． 3 ＋1 【答案】B。 【考点】菱形的性质，线段中垂线的性质，三角形三边关系，垂直线段的性质，矩形的判定和性质，锐角 三角函数定义，特殊角的三角函数值。 【分析】分两步分析： （1）若点 P，Q 固定，此时点 K 的位置：如图，作点 P 关于 BD 的对 称点 P1，连接 P1Q，交 BD 于点 K1。 由线段中垂线上的点到线段两端距离相等的性质，得 P1K1 = P K1，P1K=PK。 由三角形两边之和大于第三边的性质，得 P1K＋QK＞P1Q= P1K1＋Q K1= P K1＋Q K1。 ∴此时的 K1 就是使 PK+QK 最小的位置。 （2）点 P，Q 变动，根据菱形的性质，点 P 关于 BD 的对称点 P1 在 AB 上，即不论点 P 在 BC 上 任一点，点 P1 总在 AB 上。 因此，根据直线外一点到直线的所有连线中垂直线段最短的性 质，得，当 P1Q⊥AB 时 P1Q 最短。 过点 A 作 AQ1⊥DC 于点 Q1。 ∵∠A=120°，∴∠DA Q1=30°。 30 又∵AD=AB=2，∴P1Q=AQ1=AD·cos300= 3233。 综上所述，PK+QK 的最小值为 3 。故选 B。 例 2：（2012 四川攀枝花 4 分）如图，正方形 ABCD 中，AB=4，E 是 BC 的中点，点 P 是对角线 AC 上一 动点，则 PE+PB 的最小值为 ▲ ． 【答案】 25。 【考点】轴对称（最短路线问题），正方形的性质，勾股定理。 【分析】连接 DE，交 BD 于点 P，连接 BD。 ∵点 B 与点 D 关于 AC 对称，∴DE 的长即为 PE+PB 的最小值。 ∵AB=4，E 是 BC 的中点，∴CE=2。 在 Rt△CDE 中， 2 2 2 2DE= CD +CE 4 +2 2 5。 例 3：（2012 福建莆田 4 分）点 A、Ｂ均在由面积为 1 的相同小矩形组成的网格的格点上，建立平面直角 坐标系如图所示．若 P 是 x 轴上使得 PA PB 的值最大的点，Q 是 y 轴上使得 QA 十 QB 的值最小的点， 则 OP OQ ＝ ▲ ． 【答案】5。 【考点】轴对称（最短路线问题），坐标与图形性质，三角形三边关系，待定系数法，直线上点的坐标与 方程的关系。 【分析】连接 AB 并延长交 x 轴于点 P，作 A 点关于 y 轴的对称点 A′连接 A′B 交 y 轴于点 Q，求出点 Q 与 y 轴的交点坐标即可得出结论： 31 连接 AB 并延长交 x 轴于点 P， 由三角形的三边关系可知，点 P 即为 x 轴上使得|PA－PB|的值最大的点。 ∵点 B 是正方形 ADPC 的中点， ∴P（3，0）即 OP=3。 作 A 点关于 y 轴的对称点 A′连接 A′B 交 y 轴于点 Q，则 A′B 即为 QA+QB 的最小值。 ∵A′（-1，2），B（2，1）， 设过 A′B 的直线为：y=kx+b， 则 2 k b 1 2k b      ，解得 1k 3 5b 3     。∴Q（0， 5 3 ），即 OQ= 5 3 。 ∴OP•OQ=3× 5 3 =5。 例 4：（2012 湖北鄂州 3 分）在锐角三角形 ABC 中，BC= 24 ，∠ABC=45°，BD 平分∠ABC，M、 N 分 别是 BD、BC 上的动点，则 CM+MN 的最小值是 ▲ 。 [ 【答案】4。 【考点】最短路线问题，全等三角形的判定和性质，三角形三边关系，垂直线段的性质，锐角三角函数定 义，特殊角的三角函数值。 【分析】如图，在 BA 上截取 BE=BN，连接 EM。 ∵∠ABC 的平分线交 AC 于点 D，∴∠EBM=∠NBM。 在△AME 与△AMN 中，∵BE=BN ，∠EBM=∠NBM，BM=BM， ∴△BME≌△BMN（SAS）。 ∴ME=MN。∴CM+MN=CM+ME≥CE。 又∵CM+MN 有最小值，∴当 CE 是点 C 到直线 AB 的距离时，CE 取最小值。 ∵BC= 42，∠ABC=45°，∴CE 的最小值为 sin450=4。 ∴CM+MN 的最小值是 4。 例 5：（2012 广西贵港 2 分）如图，MN 为⊙O 的直径，A、B 是 O 上的两点，过 A 作 AC⊥MN 于点 C， 32 过 B 作 BD⊥MN 于点 D，P 为 DC 上的任意一点，若 MN＝20，AC＝8，BD＝6，则 PA＋PB 的最小值是 ▲ 。 例 6：（2012 内蒙古赤峰 14 分）阅读材料： （1）对于任意两个数ab、 的大小比较，有下面的方法： 当 a b 0时，一定有ab ； 当 a b 0时，一定有ab ； 当 a b 0时，一定有ab ． 反过来也成立．因此，我们把这种比较两个数大小的方法叫做“求差法”． （2）对于比较两个正数 ab、 的大小时，我们还可以用它们的平方进行比较： ∵ 22a b (a b)(a b)    ，a b 0 ∴（ 22ab ）与（ ab ）的符号相同 33 当 22ab ＞0 时，ab ＞0，得ab 当 22ab =0 时，ab =0，得ab 当 22ab ＜0 时，ab ＜0，得ab 解决下列实际问题： （1）课堂上，老师让同学们制作几种几何体，张丽同学用了 3 张 A4 纸，7 张 B5 纸；李明同学用了 2 张 A4 纸，8 张 B5 纸．设每张 A4 纸的面积为 x，每张 B5 纸的面积为 y，且 x＞y，张丽同学的用纸总面积为 W1，李明同学的用纸总面积为 W2．回答下列问题： ①W1= （用 x、y 的式子表示） W2= （用 x、y 的式子表示） ②请你分析谁用的纸面积最大． （2）如图 1 所示，要在燃气管道 l 上修建一个泵站，分别向 A．B 两镇供气，已知 A．B 到 l 的距离分别 是 3km、4km（即 AC=3km，BE=4km）， AB=xkm，现设计两种方案： 方案一：如图 2 所示，AP⊥l 于点 P，泵站修建在点 P 处，该方案中管道长度 a1=AB+AP． 方案二：如图 3 所示，点 A′与点 A 关于 l 对称，A′B 与 l 相交于点 P，泵站修建在点 P 处，该方案中管道 长度 a2=AP+BP． ①在方案一中，a1= km（用含 x 的式子表示）； ②在方案二中，a2= km（用含 x 的式子表示）； ③请你分析要使铺设的输气管道较短，应选择方案一还是方案二． 【答案】解：（1）①3x+7y；2x+8y。 ②W1﹣W2=（3x+7y）﹣（2x+8y）=x﹣y， ∵x＞y，∴x﹣y＞0。∴W1﹣W2＞0。 ∴W1＞W2，所以张丽同学用纸的总面积大。 （2）①x+3。 34 ② 2x 48 。 ③∵    222 2 2 2 2 12a a = x+3 x +48 =x +6x+9 x 48=6x 39     ∴当 22 12aa ＞0（即 a1﹣a2＞0，a1＞a2）时，6x﹣39＞0，解得 x＞6.5； 当 22 12aa =0（即 a1﹣a2=0，a1=a2）时，6x﹣39=0，解得 x=6.5； 当 22 12aa ＜0（即 a1﹣a2＜0，a1＜a2）时，6x﹣39＜0，解得 x＜6.5。 综上所述，当 x＞6.5 时，选择方案二，输气管道较短， 当 x=6.5 时，两种方案一样， 当 0＜x＜6.5 时，选择方案一，输气管道较短。 例 7：（2012 山东滨州 10 分）如图，在平面直角坐标系中，抛物线 y=ax2+bx+c 经过 A（﹣2，﹣4）， O（0， 0）， B（2，0）三点． （1）求抛物线 y=ax2+bx+c 的解析式； （2）若点 M 是该抛物线对称轴上的一点，求 AM+OM 的最小值． 【答案】解：（1）把 A（﹣2，﹣4）， O（0，0）， B（2，0）三点的坐标代入 y=ax2+bx+c 中，得 35 4a+2b+c=0 4a 2b+c= 4 c=0     ，解这个方程组，得 1a= 2 b=1 c=0        。 ∴抛物线的解析式为 y=﹣ 1 2 x2+x。 （2）由 y=﹣ 1 2 x2+x=﹣ 1 2 （x﹣1）2+ 1 2 ，可得 抛物线的对称轴为 x=1，并且对称轴垂直平分线段 OB。 ∴OM=BM。∴OM+AM=BM+AM。 连接 AB 交直线 x=1 于 M 点，则此时 OM+AM 最小。 过点 A 作 AN⊥x 轴于点 N， 在 Rt△ABN 中， 2 2 2 2AB= AN +BN 4 +4 4 2， 因此 OM+AM 最小值为 42。 【考点】二次函数综合题，曲线上点的坐标与方程的关系，解方程组，二次函数的性质，线段中垂线的性 质，三角形三边关系，勾股定理。 【分析】（1）已知抛物线上不同的三点坐标，利用待定系数法可求出该抛物线的解析。 （2）根据 O、B 点的坐标发现：抛物线上，O、B 两点正好关于抛物线的对称轴对称，那么只需 连接 A、B，直线 AB 和抛物线对称轴的交点即为符合要求的 M 点，而 AM+OM 的最小值正好是 AB 的长。 对 x=1 上其它任一点 M′，根据三角形两边之和大于第三边的性质，总有： O M′+A M′= B M′+A M′＞AB=OM+AM， 即 OM+AM 为最小值。 例 8：（2012 山西省 14 分）综合与实践：如图，在平面直角坐标系中，抛物线 y=﹣x2+2x+3 与 x 轴交于 A．B 两点，与 y 轴交于点 C，点 D 是该抛物线的顶点． （1）求直线 AC 的解析式及 B．D 两点的坐标； 36 （2）点 P 是 x 轴上一个动点，过 P 作直线 l∥AC 交抛物线于点 Q，试探究：随着 P 点的运动，在抛物线 上是否存在点 Q，使以点 A．P、Q、C 为顶点的四边形是平行四边形？若存在，请直接写出符合条件的点 Q 的坐标；若不存在，请说明理由． （3）请在直线 AC 上找一点 M，使△BDM 的周长最小，求出 M 点的坐标． 【答案】解：（1）当 y=0 时，﹣x2+2x+3=0，解得 x1=﹣1，x2=3。 ∵点 A 在点 B 的左侧，∴A．B 的坐标分别为（﹣1，0），（3，0）。 当 x=0 时，y=3。∴C 点的坐标为（0，3）。 设直线 AC 的解析式为 y=k1x+b1（k1≠0），则 1 11 b =3 k +b =0   ，解得 1 1 k =3 b =3    。 ∴直线 AC 的解析式为 y=3x+3。 ∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点 D 的坐标为（1，4）。 （2）抛物线上有三个这样的点 Q。如图， ①当点 Q 在 Q1 位置时，Q1 的纵坐标为 3，代入抛物线可得点 Q1 的坐标为（2，3）； ②当点 Q 在点 Q2 位置时，点 Q2 的纵坐标为﹣3，代入抛物线 可得点 Q2 坐标为（1+ 7 ，﹣3）； ③当点 Q 在 Q3 位置时，点 Q3 的纵坐标为﹣3，代入抛物线解 析式可得，点 Q3 的坐标为（1﹣ ，﹣3）。 综上可得满足题意的点 Q 有三个，分别为：Q1（2，3）， Q2（1+ ，﹣3）， Q3（1﹣ ，﹣3）。 （3）点 B 作 BB′⊥AC 于点 F，使 B′F=BF，则 B′为点 B 关于直线 AC 的对称点．连接 B′D 交直线 AC 与点 M，则点 M 为所求。 过点 B′作 B′E⊥x 轴于点 E。 37 ∵∠1 和∠2 都是∠3 的余角，∴∠1=∠2。 ∴Rt△AOC∽Rt△AFB。∴ CO CA=BF AB 。 由 A（﹣1，0）， B（3，0）， C（0，3）得 OA=1，OB=3，OC=3， ∴AC= 10 ，AB=4。 ∴ 3 10=BF 4 ，解得 6 10BF= 5 。∴BB′=2BF= 12 10 5 ， 由∠1=∠2 可得 Rt△AOC∽Rt△B′EB，∴ AO CO CA==B E BE BB 。 ∴ 1 3 10==B E BE 12 10 5  。∴B′E=12 5 ，BE= 36 5 。∴OE=BE﹣OB= ﹣3= 21 5 ． ∴B′点的坐标为（﹣ ， ）。 设直线 B′D 的解析式为 y=k2x+b2（k2≠0），则 22 22 k +b =4 21 12k +b =55  ，解得 2 2 4k=13 48b=13     。 ∴直线 B'D 的解析式为： 4 48y= x+13 13 。 联立 B'D 与 AC 的直线解析式可得： y 3x 3 4 48y= x+13 13   ，解得 9x= 35 132y= 35     。 ∴M 点的坐标为（ 9 132 35 35 ， ）。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，二次函数的性质，平行四边形的 性质，轴对称的性质，直角三角形两锐角的关系，三角形三边关系，勾股定理，相似三角形的判定和性质， 解二元一次方程组。 【分析】（1）根据点在曲线上，点的坐标满足方程的关系，由抛物线 y=﹣x2+2x+3 与 x 轴交于 A．B 两点 可求得 A．B 两点的坐标，同样，由由抛物线 y=﹣x2+2x+3 与 y 轴交于点 C 可求得 C 点的坐标。用待定系 数法，可求得直线 AC 的解析式。由 y=﹣x2+2x+3=﹣（x﹣1）2+4 可求得顶点 D 的坐标。 （2）由于点 P 在 x 轴上运动，故由平行四边形对边平行的性质求得点 Q 的坐标。 （3）点 B 作 BB′⊥AC 于点 F，使 B′F=BF，则 B′为点 B 关于直线 AC 的对称点．连接 B′D 交直 38 线 AC 与点 M，则根据轴对称和三角形三边关系，知点 M 为所求。 因此，由勾股定理求得 AC= 10 ，AB=4。由 Rt△AOC∽Rt△AFB 求得 6 10BF= 5 ，从而得 到 BB′=2BF= 12 10 5 。由 Rt△AOC∽Rt△B′EB 得到 B′E=12 5 ，BE= 36 5 ，OE=BE﹣OB= ﹣3= 21 5 ，从 而得到点 B′的坐标。用待定系数法求出线 B′D 的解析式，与直线 AC 的解析式即可求得点 M 的坐标。 例 9：（2012 湖北恩施 8 分）如图，已知抛物线 y=﹣x2+bx+c 与一直线相交于 A（﹣1，0）， C（2，3）两 点，与 y 轴交于点 N．其顶点为 D． （1）抛物线及直线 AC 的函数关系式； （2）设点 M（3，m），求使 MN+MD 的值最小时 m 的值； （3）若抛物线的对称轴与直线 AC 相交于点 B，E 为直线 AC 上的任意一点，过点 E 作 EF∥BD 交抛物线于 点 F，以 B，D，E，F 为顶点的四边形能否为平行四边形？若能，求点 E 的坐标；若不能，请说明理由； （4）若 P 是抛物线上位于直线 AC 上方的一个动点，求△APC 的面积的最大值． 【答案】解：（1）由抛物线 y=﹣x2+bx+c 过点 A（﹣1，0）及 C（2，3）得， 1 b+c=0 4+2b+c=3   ，解得 b=2 c=3    。∴抛物线的函数关系式为 2y x 2x 3    。 设直线 AC 的函数关系式为 y=kx+n，由直线 AC 过点 A（﹣1，0）及 C（2，3）得 k+n=0 2k+n=3    ，解得 k=1 n=1    。∴直线 AC 的函数关系式为 y=x+1。 （2）作 N 点关于直线 x=3 的对称点 N′， 令 x=0，得 y=3，即 N（0，3）。 39 ∴N′（6，3） 由  22y x 2x 3= x 1 +4      得 D（1，4）。 设直线 DN′的函数关系式为 y=sx+t，则 6s+t=3 s+t=4    ，解得 1s= 5 21t= 5     。 ∴故直线 DN′的函数关系式为 1 21yx55   。 根据轴对称的性质和三角形三边关系，知当 M（3，m）在直线 DN′上时，MN+MD 的值 最小， ∴ 1 21 18m 3 =5 5 5    。 ∴使 MN+MD 的值最小时 m 的值为18 5 。 （3）由（1）、（ 2）得 D（1，4）， B（1，2）， ①当 BD 为平行四边形对角线时，由 B、C、D、N 的坐标知，四边形 BCDN 是平行四 边形，此时，点 E 与点 C 重合，即 E（2，3）。 ②当 BD 为平行四边形边时， ∵点 E 在直线 AC 上，∴设 E（x，x+1），则 F（x， 2x 2x 3   ）。 又∵BD=2 ∴若四边形 BDEF 或 BDFE 是平行四边形时，BD=EF。 ∴  2x 2x 3 x 1 =2     ，即 2x x 2 =2   。 若 2x x 2=2   ，解得，x=0 或 x=1（舍去），∴E（0，1）。 若 2x x 2= 2    ，解得， 1 17x= 2  ，∴E 1+ 17 3+ 17 22   ， 或 E 1 17 3 17 22  ， 。 综上，满足条件的点 E 为（2，3）、（ 0，1）、 、 。 （4）如图，过点 P 作 PQ⊥x 轴交 AC 于点 Q；过点 C 作 CG⊥x 轴于点 G， 40 设 Q（x，x+1），则 P（x，﹣x2+2x+3）。 ∴ 22PQ x 2x 3 x 1 x x 2         （ ）（ ） 。 ∴ APC APQ CPQ 1S S +S PQ AG2     221 3 1 27x x 2 3 x2 2 2 8        （ ） （ ） 。 ∵ 3 02 < ， ∴当 1x= 2 时，△APC 的面积取得最大值，最大值为 27 8 。 例10：（2012湖北黄冈14分）如图，已知抛物线的方程C1:    1y x 2 (x m) m 0m     与x 轴相交于 点B、 C，与y 轴相交于点E，且点B 在点C 的左侧. (1)若抛物线C1过点M(2，2)，求实数m 的值． (2)在(1)的条件下，求△BCE的面积． (3)在(1)的条件下，在抛物线的对称轴上找一点H，使BH+EH最小，并求出点H的坐标． (4)在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似?若存在， 求m的值；若不存在，请说明理由． 41 【答案】解：（1）∵抛物线 C1 过点 M(2，2)，∴  12 2 2 (2 m)m    ，解得 m=4。 （2）由（1）得  1y x 2 (x 4)4    。 令 x=0，得 y2 。∴E（0，2）， OE=2。 令 y=0，得  10 x 2 (x 4)4    ，解得 x1=－2，x=4。 ∴B（－2，， 0）， C（4，0）， BC=6。 ∴△BCE 的面积= 1 6 2 62    。 （3）由（2）可得 的对称轴为 x=1。 连接 CE，交对称轴于点 H，由轴对称的性质和两点之间线段 最短的性质，知此时 BH+EH 最小。 设直线 CE 的解析式为 y kx+b ，则 4k+b=0 b=2    ，解得 1k= 2 b=2    。∴直线 CE 的解析式为 1y x+22 。 当 x=1 时， 3y 2 。∴H（1， 3 2 ）。 （4）存在。分两种情形讨论： ①当△BEC∽△BCF 时，如图所示。 则 BE BC BC BF ，∴BC2=BE•BF。 由（2）知 B（－2，0）， E（0，2），即 OB=OE， ∴∠EBC=45°，∴∠CBF=45°。 作 FT⊥x 轴于点 F，则 BT=TF。 ∴令 F（x，－x－2）（ x＞0）， 又点 F 在抛物线上，∴－x－2=  1 x 2 (x m)m   ， ∵x+2＞0（∵x＞0）， ∴x=2m，F（2m，－2m－2）。 此时 22BF (2m 2) ( 2m 2) 2 2 m 1 BE 2 2 BC m 2         （ ）， ， ， 又 BC2=BE•BF，∴（m+2）2= 22 • 2 2 m 1（ ），解得 m=2± 。 ∵m＞0，∴m= +2。 42 ②当△BEC∽△FCB 时，如图所示。 则 BC EC BF BC ，∴BC2=EC•BF。 同①，∵∠EBC=∠CFB，△BTF∽△COE， ∴ TF OE 2 BT OC m。 ∴令 F（x，－ 2 m （x+2））（x＞0）， 又点 F 在抛物线上，∴－ （x+2）=  1 x 2 (x m)m   。 ∵x+2＞0（∵x＞0）， ∴x=m+2。∴F（m+2，－ （m+4））， 2EC m 4，BC=m+2。 又 BC2=EC•BF，∴（m+2）2=    2 22 2 4 m+4m 4 m+2+2 + m  . 整理得：0=16，显然不成立。 综合①②得，在第四象限内，抛物线上存在点 F，使得以点 B、C、F 为顶点的三角形 与△BCE 相似，m= 22+2。 【考点】二次函数综合题，曲线上点的坐标与方程的关系，二次函数的性质，轴对称的性质，两点之间线 段最短的性质，相似三角形的判定和性质。 【分析】（1）将点（2，2）的坐标代入抛物线解析式，即可求得 m 的值。 （2）求出 B、C、E 点的坐标，从而求得△BCE 的面积。 （3）根据轴对称以及两点之间线段最短的性质，可知点 B、C 关于对称轴 x=1 对称，连接 EC 与 对称轴的交点即为所求的 H 点。 （4）分两种情况进行讨论： ①当△BEC∽△BCF 时，如图所示，此时可求得 +2。 ②当△BEC∽△FCB 时，如图所示，此时得到矛盾的等式，故此种情形不存在。 例 11：（2012 黑龙江黑河、齐齐哈尔、大兴安岭、鸡西 6 分） 如图，抛物线 21y x=x2 bc 与 x 轴交 于 A、B 两点，与 y 轴交于点 C，且 OA=2，OC=3． (1)求抛物线的解析式． (2)若点 D(2，2)是抛物线上一点，那么在抛物线的对称轴上，是否存在一点 P，使得△BDP 的周长最小， 若存在，请求出点 P 的坐标，若不存在，请说明理由． 43 注：二次函数 2y ax bx c   （a ≠0）的对称轴是直线x = b 2a 【答案】解：（1）∵OA=2，OC=3，∴A（－2，0）， C（0，3）。 将 C（0，3）代入 21y= x bx c2   得 c=3。 将 A（－2，0）代入 21y= x bx 32   得，    210= 2 2 b 32      ，解得 b= 1 2 。 ∴抛物线的解析式为 211y= x x 322   。 （2）如图：连接 AD，与对称轴相交于 P，由于点 A 和点 B 关于对称轴对称，则即 BP+DP=AP+DP，当 A、P、D 共线时 BP+DP=AP+DP 最小。 设 AD 的解析式为 y=kx+b， 将 A（-2，0）， D（2，2）分别代入解析式得， 2k b 0 2k b 2      ，解得， 1k 2 b1     ，∴直线 AD 解析式为 y= 1 2 x+1。 ∵二次函数的对称轴为 1 12x 1 22 2     ， ∴当 x= 时，y= × +1= 5 4 。∴P（ ， ）。 【考点】曲线上点的坐标与方程的关系，轴对称（最短路线问题）。 【分析】（1）根据 OC=3，可知 c=3，于是得到抛物线的解析式为 21y= x bx 32   ，然后将 A（－2，0） 代入解析式即可求出 b 的值，从而得到抛物线的解析式。 （2）由于 BD 为定值，则△BDP 的周长最小，即 BP＋DP 最小，由于点 A 和点 B 关于对称轴对 称，则即 BP+DP=AP+DP，当 A、P、D 共线时 BP+DP=AP+DP 最小。 例 12：（2012 湖南郴州 10 分）如图，已知抛物线 2y ax bx c   经过 A（4，0）， B（2，3）， C（0，3） 三点． 44 （1）求抛物线的解析式及对称轴． （2）在抛物线的对称轴上找一点 M，使得 MA+MB 的值最小，并求出点 M 的坐标． （3）在抛物线上是否存在一点 P，使得以点 A、B、C、P 四点为顶点所构成的四边形为梯形？若存在， 请求出点 P 的坐标；若不存在，请说明理由． 【答案】解：（1）∵抛物线 2y ax bx c   经过 A（4，0）， B（2，3）， C（0，3）三点， ∴ 16a 4b c 0 4a 2b c 3 c 3          ，解得 3a 8 3b 4 c3        。 ∴抛物线的解析式为： 233y x x 384    ，其对称轴为： bx12a   。 （2）由 B（2，3）， C（0，3），且对称轴为 x=1，可知点 B、 C 是关于对称轴 x=1 的对称点。 如图 1 所示，连接 AC，交对称轴 x=1 于点 M，连接 MB，则 MA＋MB=MA＋MC=AC，根据两点之间线段最短可知此时 MA ＋MB 的值最小。 设直线 AC 的解析式为 y=kx＋b， ∵A（4，0）， C（0，3）， ∴ 4k b 0 b 3    ，解得 3k 4 b3     。 ∴直线 AC 的解析式为：y= 3 4 x＋3。 令 x=1，得 y= 9 4 。∴M 点坐标为（1， ）。 （3）结论：存在。 45 如图 2 所示，在抛物线上有两个点 P 满足题意： ①若 BC∥AP1，此时梯形为 ABCP1。 由 B（2，3）， C（0，3），可知 BC∥x 轴，则 x 轴与 抛物线的另一个交点 P1 即为所求。 在 233y x x 384    中令 y=0，解得 x1=-2，x2=4。 ∴P1（－2，0）。 ∵P1A=6，BC=2，∴P1A≠BC。 ∴四边形 ABCP1 为梯形。 ②若 AB∥CP2，此时梯形为 ABCP2。 设 CP2 与 x 轴交于点 N， ∵BC∥x 轴，AB∥CP2，∴四边形 ABCN 为平行四边形。∴AN=BC=2。∴N（2，0）。 设直线 CN 的解析式为 y=k1x+b1，则有： 11 1 2k b 0 b 3    ，解得 3k 2 b3     。 ∴直线 CN 的解析式为：y= 3 2 x+3。 ∵点 P2 既在直线 CN：y= x+3 上，又在抛物线： 上， ∴ x+3= 233 x x 384   ，化简得：x2－6x=0，解得 x1=0（舍去），x2=6。 ∴点 P2 横坐标为 6，代入直线 CN 解析式求得纵坐标为－6。∴P2（6，－6）。 ∵ ABCN，∴AB=CN，而 CP2≠CN，∴CP2≠AB。∴四边形 ABCP2 为梯形。 综上所述，在抛物线上存在点 P，使得以点 A、B、C、P 四点为顶点所构成的四边形为 梯形，点 P 的坐标为（－2，0）或（6，－6）。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，二次函数的性质，轴对称的性质， 线段最短的性质，梯形的判定。 【分析】（1）已知抛物线上三点 A、B、C 的坐标，利用待定系数法即可求出抛物线的解析式，再由对称 轴公式 bx 2a 求出对称轴。 （2）如图 1 所示，连接 AC，则 AC 与对称轴的交点即为所求之 M 点；已知点 A、C 的坐标，利 用待定系数法求出直线 AC 的解析式，从而求出点 M 的坐标。 （3）根据梯形定义确定点 P，如图 2 所示：①若 BC∥AP 1，确定梯形 ABCP1．此时 P1 为抛物线 46 与 x 轴的另一个交点，解一元二次方程即可求得点 P1 的坐标；②若 AB∥CP2，确定梯形 ABCP2．此时 P2 位于第四象限，先确定 CP2 与 x 轴交点 N 的坐标，然后求出直线 CN 的解析式，再联立抛物线与直线解析 式求出点 P2 的坐标。 例 13：（2012 四川凉山 8 分）在学习轴对称的时候，老师让同学们思考课本中的探究题。 如图（1），要在燃气管道 l 上修建一个泵站，分别向 A、B 两镇供气．泵站修在管道的什么地方， 可使所用的输气管线最短？ 你可以在 l 上找几个点试一试，能发现什么规律？你可以在l 上找几个点试一试，能发现什么规 律？ 聪明的小华通过独立思考，很快得出了解决这个问题的正确办法．他把管道 l 看成一条直线（图（2）），问 题就转化为，要在直线 l 上找一点 P，使 AP 与 BP 的和最小．他的做法是这样的： ①作点 B 关于直线 l 的对称点 B′． ②连接 AB′交直线 l 于点 P，则点 P 为所求． 请你参考小华的做法解决下列问题．如图在△ABC 中，点 D、E 分别是 AB、AC 边的中点，BC=6，BC 边上的高为 4，请你在 BC 边上确定一点 P，使△PDE 得周长最小． （1）在图中作出点 P（保留作图痕迹，不写作法）． （2）请直接写出△PDE 周长的最小值： ． 【答案】解：（1）作 D 点关于 BC 的对称点 D′，连接 D′E，与 BC 交于点 P，P 点即为所求。 47 （2）8． 【考点】轴对称（最短路线问题），三角形三边关系，三角形中位线定理，勾股定理。 【分析】（1）根据提供材料 DE 不变，只要求出 DP+PE 的最小值即可，作 D 点关于 BC 的对称点 D′，连 接 D′E，与 BC 交于点 P，P 点即为所求。 （2）利用中位线性质以及勾股定理得出 D′E 的值，即可得出答案： ∵点 D、E 分别是 AB、AC 边的中点，∴DE 为△ABC 中位线。 ∵BC=6，BC 边上的高为 4，∴DE=3，DD′=4。 ∴ 2 2 2 2D E DE DD 3 4 5       。 ∴△PDE 周长的最小值为：DE+D′E=3＋5=8。 例 14：（2012 湖北十堰 6 分）阅读材料： 例：说明代数式 22x 1 (x 3) 4   ＋ 的几何意义，并求它的最小值． 解： 2 2 2 2 2 2x 1 (x 3) 4 (x 0) 1 (x 3) 2          ，如图，建立平面直角坐标系，点 P（x，0） 是 x 轴上一点，则 22(x 0) 1可以看成点 P 与点 A（0，1）的距离， 22(x 3) 2可以看成点 P 与点 B（3，2）的距离，所以原代数式的值可以看成线段 PA 与 PB 长度之和，它的最小值就是 PA＋PB 的最小 值． 设点 A 关于 x 轴的对称点为 A′，则 PA=PA′，因此，求 PA＋PB 的最小值，只需求 PA′＋PB 的最小值，而 点 A′、B 间的直线段距离最短，所以 PA′＋PB 的最小值为线段 A′B 的长度．为此，构造直角三角形 A′CB， 因为 A′C=3，CB=3，所以 A′B=3 2 ，即原式的最小值为 3 。 48 根据以上阅读材料，解答下列问题： （1）代数式 22(x 1) 1 (x 2) 9     的值可以看成平面直角坐标系中点 P（x，0）与点 A（1，1）、点 B 的距离之和．（填写点 B 的坐标） （2）代数式 22x 49 x 12x 37    的最小值为 ． 【答案】解：（1）（ 2，3）。 （2）10。 【考点】坐标与图形性质，轴对称（最短路线问题）。 【分析】（1）∵原式化为 2 2 2 2(x 1) 1 (x 2) 3     的形式， ∴代数式 22(x 1) 1 (x 2) 9     的值可以看成平面直角坐标系中点 P（x，0）与点 A （1，1）、点 B（2，3）的距离之和。 （2）∵原式化为 2 2 2 2(x 0) 7 (x 6) 1     的形式， ∴所求代数式的值可以看成平面直角坐标系中点 P（x，0）与点 A（0，7）、点 B（6，1） 的距离之和。 如图所示：设点 A 关于 x 轴的对称点为 A′，则 PA=PA′， ∴求 PA＋PB 的最小值，只需求 PA′＋PB 的最小值，而点 A′、B 间的直线段距离最短。 ∴PA′＋PB 的最小值为线段A′B 的长度。 ∵A（0，7）， B（6，1）， ∴A′（0，－7）， A′C=6，BC=8。 ∴ 2 2 2 2A B A C BC 6 8 =10      。 例 15：（2012 甘肃兰州 12 分）如图，Rt△ABO 的两直角边 OA、OB 分别在 x 轴的负半轴和 y 轴的正半轴 上，O 为坐标原点，A、B 两点的坐标分别为(－3，0)、(0，4)，抛物线 y＝ 2 3 x2＋bx＋c 经过点 B，且顶点 在直线 x＝ 5 2 上． (1)求抛物线对应的函数关系式； 49 (2)若把△ABO 沿 x 轴向右平移得到△DCE，点 A、B、O 的对应点分别是 D、C、E，当四边形 ABCD 是 菱形时，试判断点 C 和点 D 是否在该抛物线上，并说明理由； (3)在(2)的条件下，连接 BD，已知对称轴上存在一点 P 使得△PBD 的周长最小，求出 P 点的坐标； (4)在(2)、(3)的条件下，若点 M 是线段 OB 上的一个动点(点 M 与点 O、B 不重合)，过点 M 作∥BD 交 x 轴于点 N，连接 PM、PN，设 OM 的长为 t，△PMN 的面积为 S，求 S 和 t 的函数关系式，并写出自变量 t 的取值范围，S 是否存在最大值？若存在，求出最大值和此时 M 点的坐标；若不存在，说明理由． 【答案】解：（1）∵抛物线 y＝ 2 3 x2＋bx＋c 经过点 B(0，4)，∴c＝4。 ∵顶点在直线 x＝ 5 2 上，∴ b5=2 22 3   ，解得 10b= 3 。 ∴所求函数关系式为 22 10y= x x+433 。 （2）在 Rt△ABO 中，OA＝3，OB＝4，∴ 22AB OA OB 5= 。 ∵四边形 ABCD 是菱形，∴BC＝CD＝DA＝AB＝5。 ∴C、D 两点的坐标分 别是(5，4)、(2，0)， 当 x＝5 时， 22 10y= 5 5+4=433   ； 当 x＝2 时， 22 10y= 2 2+4=033   。 ∴点 C 和点 D 都在所求抛物线上。 （3）设 CD 与对称轴交于点 P，则 P 为所求的点， 设直线 CD 对应的函数关系式为 y＝kx＋b， 则 5k+b=4 2k+b=0    ，解得， 4k= 3 8b= 3     。∴直线 CD 对应的函数关系式为 48y= x33 。 50 当 x＝ 5 2 时， 4 5 8 2y= =3 2 3 3 。∴P( 52 23 ， )。 （4）∵MN∥BD，∴△OMN∽△OBD。 ∴ OM ON OB OD ，即 t ON 42 ，得 tON 2 。 设对称轴交 x 于点 F，则  PFOM 1 1 2 5 5 5S PF OM OF= +t = t+2 2 3 2 4 6      梯形 。 ∵ 2 MON 1 1 1 1S OM ON= t t= t2 2 2 4      ， PME 1 1 5 1 2 1 5S NF PF= t = t+2 2 2 2 3 6 6        ， MON PMEPFOMS=S S S梯形 225 5 1 1 5 1 17t+ t t+ t + t4 6 4 6 6 4 12       (0＜t＜4)。 ∵ 2 21 17 1 17 289S= t + t= t +4 12 4 6 144    ， 1 04 < ，0＜17 6 ＜4， ∴当 17t= 6 时，S 取最大值是 289 144 。此时，点 M 的坐标为(0， )。 【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，二次函数的性质，菱形的性质， 相似三角形的判定和性质。 【分析】（1）根据抛物线 y＝ 2 3 x2＋bx＋c 经过点 B(0，4)，以及顶点在直线 x＝ 上，得出 b，c 即可。 （2）根据菱形的性质得出 C、D 两点的坐标分别是(5，4)、(2，0)，利用图象上点的性质得出 x＝ 5 或 2 时，y 的值即可。 （3）首先设直线 CD 对应的函数关系式为 y＝kx＋b，求出解析式，当 x＝ 时，求出 y 即可。 （4）利用 MN∥BD，得出△OMN∽△OBD，进而得出 ，得到 ，从而表示出△PMN 的面积，利用二次函数最值求出即可。 例 16：（2012 甘肃兰州 4 分）如图，四边形 ABCD 中，∠BAD＝120°，∠B＝∠D＝90°，在 BC、CD 上分 别找一点 M、N，使△AMN 周长最小时，则∠AMN＋∠ANM 的度数为【 】 51 A．130° B．120° C．110° D．100° 练习题： 1. （2011 福建福州 14 分）已知，如图，二次函数 2 23y ax ax a ( 0)a  图象的顶点为 H，与 x 轴交于 A、B 两点（B 在 A 点右侧），点 H、B 关于直线l ： 3 33yx对称． （1）求 A、B 两点坐标，并证明点 A 在直线 l 上； （2）求二次函数解析式； （3）过点 B 作直线 BK∥AH 交直线 于 K 点，M、N 分别为直线 AH 和直线 上的两个动点，连接 HN、NM、MK，求 HN+NM+MK 和的最小值． 52 2. （2011 贵州黔南 12 分）如图，在平面直角坐标系中，点 A 的坐标为（1， 3 ）， △AOB 的面积是 ． （1）求点 B 的坐标； （2）求过点 A、O、B 的抛物线的解析式； （3）在（2）中抛物线的对称轴上是否存在点 C，使△AOC 的周长最小？若存在，求出点 C 的坐标；若 不存在，请说明理由； （4）在（2）中 x 轴下方的抛物线上是否存在一点 P，过点 P 作 轴的垂线，交直线 AB 于点 D，线段 OD 把△AOB 分成两个三角形．使其中一个三角形面积与四边形 BPOD 面积比为 2：3？若存在，求出点 P 的 坐标；若不存在，请说明理由． 3. （四川雅安 12 分）如图，已知二次函数 cxaxy  22 )0( a 图像的顶点 M 在反比例函数 xy 3 上， 且与 x 轴交于 A，B 两点。 （1）若二次函数的对称轴为 2 1x ，试求 ca, 的值； （2）在（1）的条件下求 AB 的长； （3）若二次函数的对称轴与 x 轴的交点为 N，当 NO+MN 取最小值时，试求二次函数的解析式。 53 4. （2011 四川乐山 13 分）已知顶点为 A(1,5)的抛物线 2y ax bx c   经过点 B(5,1). (1)求抛物线的解析式; (2)如图（1）,设 C,D 分别是 x 轴、 y 轴上的两个动点，求四边形 ABCD 周长的最小值； （3）在（2）中，当四边形 ABCD 的周长最小时，作直线 CD.设点 P( xy， )( 0x  )是直线 yx 上的一个 动点，Q 是 OP 的中点，以 PQ 为斜边按图（2）所示构造等腰直角三角形 PRQ. ①当△PBR 与直线 CD 有公共点时,求 的取值范围； ②在①的条件下，记△PBR 与△COD 的公共部分的面积为 S.求 S 关于 的函数关系式，并求 S 的最大值。 5. （2011 山东莱芜 12 分）如图，在平面直角坐标系中，己知点 A（－2，－ 4 ) , OB＝2。抛物线 2y ax bx c   经过 A、O、B 三点。 （1）求抛物线的函数表达式； （2）若点 M 是抛物线对称轴上的一点，试求 MO＋MA 的最小值； （3）在此抛物线上，是否存在一点 P，使得以点 P 与点 O、A、B 为顶点的四边形是梯形。若存在，求点 P 的坐标；若不存在，请说明理由。 54 6. （2011 湖北黄石 3 分）初三年级某班有 54 名学生，所在教室有 6 行 9 列座位，用( , )mn 表示第 m 行第 n 列的座位，新学期准备调整座位，设某个学生原来的座位为 ，如果调整后的座位为( , )ij，则称该 生作了平移[ ,ab] ,m i n j   ,并称 ab 为该生的位置数。若某生的位置数为 10，则当 mn 取最小值 时， mn 的最大值为 ▲ . 7. （2011 四川南充 8 分）如图，等腰梯形 ABCD 中，AD∥BC，AD=AB=CD=2，∠C=60°，M 是 BC 的 中点． （1）求证：△MDC 是等边三角形； （2）将△MDC 绕点 M 旋转，当 MD（即 MD′）与 AB 交于一点 E，MC（即 MC′）同时与 AD 交于一点 F 时，点 E，F 和点 A 构成△AEF．试探究△AEF 的周长是否存在最小值．如果不存在，请说明理由；如果 存在，请计算出△AEF 周长的最小值． 8. （2011 四川眉山 11 分）如图，在直角坐标系中，已知点 A（0，1）， B（－4，4），将点 B 绕点 A 顺时 针方向旋转 90°得到点 C；顶点在坐标原点的拋物线经过点 B． （1）求抛物线的解析式和点 C 的坐标； （2）抛物线上一动点 P，设点 P 到 x 轴的距离为 d1，点 P 到点 A 的距离为 d2，试说明 d2=d1＋1； （3）在（2）的条件下，请探究当点 P 位于何处时，△PAC 的周长有最小值，并求出△PAC 的周长的最小 值． 55 9. （2011 辽宁本溪 3 分）如图，正方形 ABCD 的边长是 4，∠DAC 的平分线交 DC 于点 E，若点 P、Q 分别是 AD 和 AE 上的动点，则 DQ+PQ 的最小值【 】 A、2 B、4 C、 22 D、 42 10.（2011 辽宁阜新 3 分）如图，在矩形 ABCD 中，AB＝6，BC＝8，点 E 是 BC 中点，点 F 是边 CD 上的 任意一点，当△AEF 的周长最小时，则 DF 的长为【 】 A．1 B．2 C．3 D．4 11. （2011 贵州六盘水 3 分）如图，在菱形 ABCD 中，对角线 AC=6，BD=8，点 E、F 分别是边 AB、BC 的中点，点 P 在 AC 上运动，在运动过程中，存在 PE+PF 的最小值，则这个最小值是 【 】 A．3 B．4 C．5 D．6 12. （2011 甘肃天水 4 分）如图，在梯形 ABCD 中，AB∥CD，∠BAD=90°，AB=6，对角线 AC 平分∠BAD， 56 点 E 在 AB 上，且 AE=2（AE＜AD），点 P 是 AC 上的动点，则 PE+PB 的最小值是 ▲ ． 13. （2011 四川资阳 9 分）在一次机器人测试中，要求机器人从 A 出发到达 B 处．如图 1，已知点 A 在 O 的正西方 600cm 处，B 在 O 的正北方 300cm 处，且机器人在射线 AO 及其右侧(AO 下方)区域的速度为 20cm/ 秒，在射线 AO 的左侧(AO 上方)区域的速度为 10cm/秒． (1) 分别求机器人沿 A→O→B 路线和沿 A→B 路线到达 B 处所用的时间(精确到秒)；(3 分) (2) 若∠OCB=45°，求机器人沿 A→C→B 路线到达 B 处所用的时间(精确到秒)；(3 分) (3) 如图 2,作∠OAD=30°，再作 BE⊥AD 于 E,交 OA 于 P．试说明：从 A 出发到达 B 处，机器人沿 A→P→B 路线行进所用时间最短．(3 分) 14. （广东深圳 9 分）如图 1，抛物线  2 0y ax bx c a    的顶点为（1，4），交 x 轴于 A、B，交 y 轴 于 D，其中 B 点的坐标为（3，0） （1）求抛物线的解析式 （2）如图 2，过点 A 的直线与抛物线交于点 E，交 轴于点 F，其中 E 点的横坐标为 2，若直线 PQ 为抛 物线的对称轴，点 G 为 PQ 上一动点，则 轴上是否存在一点 H，使 D、G、F、H 四点围成的四边形周长 最小.若存在，求出这个最小值及 G、H 的坐标；若不存在，请说明理由. （3）如图 3，抛物线上是否存在一点 T，过点 T 作 的垂线，垂足为 M，过点 M 作直线 MN∥BD，交线 段 AD 于点 N，连接 MD，使△DNM∽△BMD，若存在，求出点 T 的坐标；若不存在，说明理由. 57 15. （2011 湖北咸宁 12 分）如图，在平面直角坐标系中，直线 43 4  xy 分别交 x 轴，y 轴于 A，B 两点， 点 C 为 OB 的中点，点 D 在第二象限，且四边形 AOCD 为矩形． （1）直接写出点 A，B 的坐标，并求直线 AB 与 CD 交点的坐标； （2）动点 P 从点 C 出发，沿线段 CD 以每秒 1 个单位长度的速度向终点 D 运动；同时，动点 M 从点 A 出发，沿线段 AB 以每秒 3 5 个单位长度的速度向终点 B 运动，过点 P 作 PH⊥OA，垂足为 H，连接 MP， MH．设点 P 的运动时间为t 秒． ①若△MPH 与矩形 AOCD 重合部分的面积为 1，求 的值； ②点 Q 是点 B 关于点 A 的对称点，问 BP+PH+HQ 是否有最小值，如果有，求出相应的点 P 的坐标；如果 没有，请说明理由． 16. （2011 云南昆明 12 分）如图，在 Rt△ABC 中，∠C=90°，AB=10cm，AC：BC=4：3，点 P 从点 A 出 发沿 AB 方向向点 B 运动，速度为 1cm/s，同时点 Q 从点 B 出发沿 B→C→A 方向向点 A 运动，速度为 2cm/s， 当一个运动点到达终点时，另一个运动点也随之停止运动． （1）求 AC、BC 的长； （2）设点 P 的运动时间为 x（秒），△PBQ 的面积为 y（cm2），当△PBQ 存在时，求 y 与 x 的函数关系式， 并写出自变量 x 的取值范围； （3）当点 Q 在 CA 上运动，使 PQ⊥AB 时，以点 B、P、Q 为定点的三角形与△ABC 是否相似，请说明 理由； （4）当 x=5 秒时，在直线 PQ 上是否存在一点 M，使△BCM 得周长最小，若存在，求出最小周长，若不 58 存在，请说明理由． 17. （2011 贵州安顺 12 分）如图，抛物线 y= 1 2 x2+bx﹣2 与 x 轴交于 A，B 两点，与 y 轴交于 C 点，且 A（﹣1，0）． （1）求抛物线的解析式及顶点 D 的坐标； （2）判断△ABC 的形状，证明你的结论； （3）点 M（m，0）是 x 轴上的一个动点，当 MC+MD 的值最小时，求 m 的值．