2010中考数学台州考试试题 12页

‎ 2010年台州市初中学业水平考试 数学试题卷 亲爱的考生：‎ 欢迎参加考试！请你认真审题，仔细答题，发挥最佳水平。请注意以下几点：‎ ‎1.全卷共6页，满分150分，考试时间120分钟。‎ ‎2.答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上无效。‎ ‎3.答题前，请认真阅读答题纸上的《注意事项》，按规定答题。本次考试不得使用计算器。‎ ‎ 祝你成功！　‎ 一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）‎ ‎1．的绝对值是(▲)‎ ‎ A．4 B． C． 　D．‎ ‎2．下列立体图形中，侧面展开图是扇形的是(▲)‎ A．‎ B．‎ C．‎ D．‎ C A B P ‎ ‎ ‎（第3题）‎ ‎3．如图，△ABC中，∠C=90°，AC=3，点P是边BC上的动点，‎ 则AP长不可能是(▲)‎ A．2.5 B．‎3 C．4 D．5 ‎ ‎4．下列运算正确的是(▲)‎ ‎（第5题）‎ A B O C D A． B． C． 　D． ‎ ‎5．如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠CDB大小为 (▲)‎ A．25° B．30° C．40° D．50°‎ ‎6．下列说法中正确的是(▲)‎ ‎ A．“打开电视，正在播放《新闻联播》”是必然事件；‎ ‎ B．某次抽奖活动中奖的概率为，说明每买100张奖券，一定有一次中奖；‎ ‎ C．数据1，1，2，2，3的众数是3；‎ ‎ D．想了解台州市城镇居民人均年收入水平，宜采用抽样调查．‎ ‎7．梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，则下底BC的长是(▲)‎ A．3 B．‎4 ‎‎ C． 2 D．2+2 ‎ ‎8．反比例函数图象上有三个点，，，其中 ‎，‎ 则，，的大小关系是(▲)‎ ‎ ‎ ‎ A． B．　　 C．　　 D．‎ ‎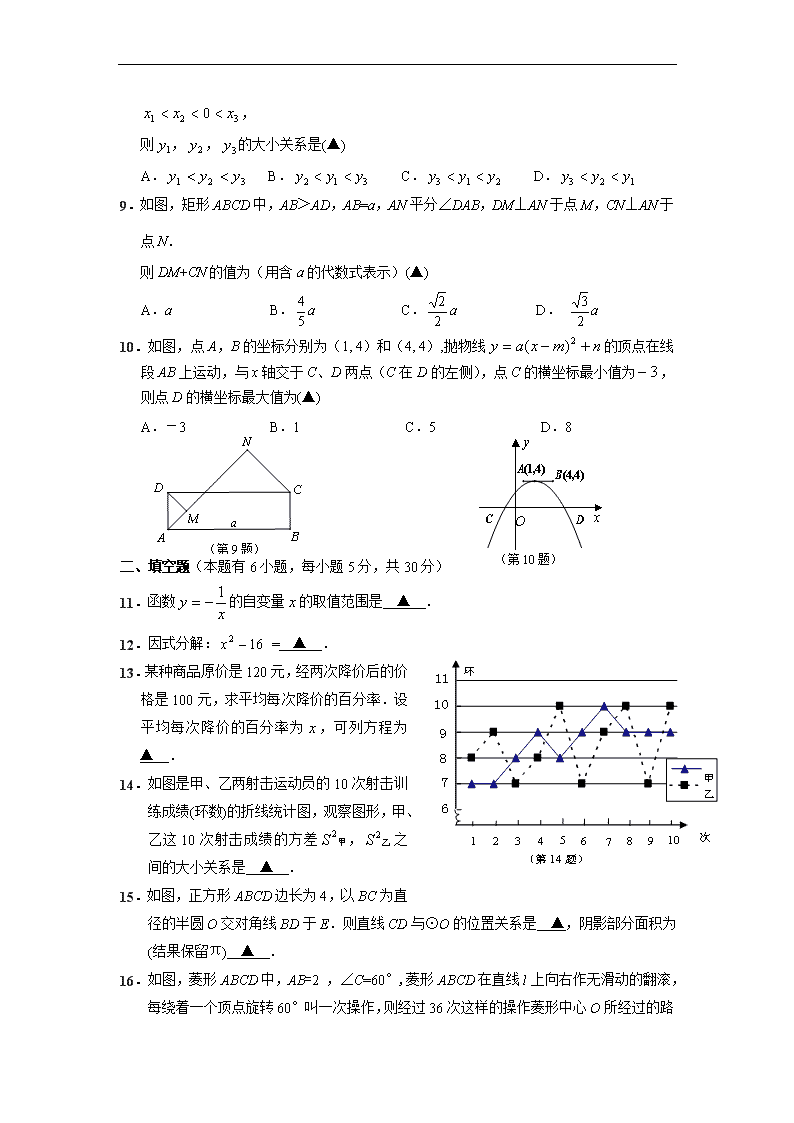9．如图，矩形ABCD中，AB＞AD，AB=a，AN平分∠DAB，DM⊥AN于点M，CN⊥AN于点N．‎ 则DM+CN的值为（用含a的代数式表示）(▲)‎ ‎ A．a B． 　 C． D． ‎ ‎10．如图，点A，B的坐标分别为（1, 4）和（4, 4）,抛物线的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为，则点D的横坐标最大值为(▲)‎ y x O ‎（第10题）‎ ‎（第9题）‎ ‎ A．－3 　 B．‎1 ‎‎ C．5 D．8 ‎ 二、填空题（本题有6小题，每小题5分，共30分）‎ ‎11．函数的自变量的取值范围是 ▲ ．‎ ‎12．因式分解： = ▲ ．‎ ‎13．某种商品原价是120元，经两次降价后的价格是100元，求平均每次降价的百分率．设平均每次降价的百分率为，可列方程为 ▲ ． ‎ ‎14．如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图，观察图形，甲、乙这10次射击成绩的方差，之间的大小关系是 ▲ ．‎ ‎15．如图，正方形ABCD边长为4，以BC为直径的半圆O交对角线BD于E．则直线CD与⊙O的位置关系是 ▲ ，阴影部分面积为(结果保留π) ▲ ． ‎ ‎16．如图，菱形ABCD中，AB=2 ，∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过36次这样的操作菱形中心O 所经过的路径总长为(结果保留π) ▲ ．‎ A B C D O E ‎（第15题）‎ O A B C ‎(第16题)‎ l D 三、解答题（本题有8小题，第17~20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）‎ ‎17．（1）计算：； ‎ ‎（2）解方程： ．‎ 参考数据 cos20°0.94，‎ sin20°0.34，‎ sin18°0.31，‎ cos18°0.95‎ ‎18．解不等式组，并把解集在数轴上表示出来．‎ ‎19．施工队准备在一段斜坡上铺上台阶方便通行．现测得斜坡上铅垂的两 棵树间水平距离AB=‎4米‎，‎斜面距离BC=‎4.25米‎，‎斜坡总长DE‎=‎85米．‎ ‎（1）求坡角∠D的度数（结果精确到1°）；‎ ‎（2）若这段斜坡用厚度为‎17cm的长方体台阶来铺，需要铺几级台阶?‎ ‎17cm ‎（第19题）‎ A B C D E F ‎20．A，B两城相距600千米，甲、乙两车同时从A城出发驶向B城，甲车到达B城后立即返回．如图是它们离A城的距离y（千米）与行驶时间 x（小时）之间的函数图象．‎ ‎（1）求甲车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；‎ x/小时 y/千米 ‎600‎ ‎14‎ ‎6‎ O F E C D ‎（第20题）‎ ‎（2）当它们行驶7了小时时，两车相遇，求乙车速度．‎ ‎21．果农老张进行杨梅科学管理试验．把一片杨梅林分成甲、乙两部分，甲地块用新技术管理，乙地块用老方法管理，管理成本相同．在甲、乙两地块上各随机选取20棵杨梅树，根据每棵树产量把杨梅树划分成A，B，C，D，E五个等级（甲、乙的等级划分标准相同，每组数据包括左端点不包括右端点）．画出统计图如下：‎ 乙地块杨梅等级分布扇形统计图 甲地块杨梅等级频数分布直方图 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ 产量/kg 频数 A B C D E ‎(第21题)‎ ‎0‎ ‎（1）补齐直方图，求的值及相应扇形的圆心角度数；‎ ‎（2）选择合适的统计量，比较甲乙两地块的产量水平，并说明试验结果；‎ ‎（3）若在甲地块随机抽查1棵杨梅树，求该杨梅树产量等级是B的概率．‎ ‎22．类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（）=1．‎ ‎ 　　若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为．‎ ‎ 解决问题：（1）计算：{3，1}+{1，2}；{1，2}+{3，1}．‎ ‎ （2）①动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”‎ ‎{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”‎ ‎{3，1}平移，最后的位置还是点B吗? 在图1中画出四边形OABC.‎ ‎②证明四边形OABC是平行四边形.‎ ‎（3）如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O. 请用“平移量”加法算式表示它的航行过程．‎ ‎（第22题）‎ y O 图2‎ Q（5, 5）‎ P（2, 3）‎ y O 图1‎ ‎1‎ ‎1‎ x x ‎23．如图1，Rt△ABC≌Rt△EDF，∠ACB=∠F=90°，∠A=∠E=30°．△EDF绕着边AB的中点D旋转， DE，DF分别交线段AC于点M，K．‎ ‎ （1）观察： ①如图2、图3，当∠CDF=0° 或60°时，AM+CK_______MK(填“>”，“<”或“=”)．‎ ‎②如图4，当∠CDF=30° 时，AM+CK___MK(只填“>”或“<”)．‎ ‎（2）猜想：如图1，当0°＜∠CDF＜60°时，AM+CK_______MK，证明你所得到的结论．‎ 图1‎ 图2‎ 图3‎ ‎（第23题）‎ 图4‎ ‎（3）如果，请直接写出∠CDF的度数和的值．‎ ‎（第24题）‎ H ‎24．如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B以Q，P为对称中心的对称点， HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．‎ ‎（1）求证：△DHQ∽△ABC；‎ ‎（2）求y关于x的函数解析式并求y的最大值；‎ ‎（3）当x为何值时，△HDE为等腰三角形？‎ ‎ ‎ ‎2010年台州市初中学业水平考试 数学参考答案和评分细则 一、选择题（本题有10小题，每小题4分，共40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A ‎ B A C A D B B C D 二、填空题(本题有6小题，每小题5分，共30分)‎ ‎11． 12． 13． ‎ ‎14．＜ 15．相切（2分），π （3分） 16．（8+4）π 三、解答题(本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分)‎ ‎17．（8分）（1）解：原式=2+1+1　…………………………………………………………3分 ‎ =4 ………………………………………………………………1分 ‎（2）解： ‎ ‎ 　　． ……………………………………………………………………3分 ‎①②‎ 经检验：是原方程的解．…………………………………………………………1分 所以原方程的解是．‎ ‎18．（8分）‎ 解①得，＜3， ……………………………………………………………………2分 解②得，＞1， ………………………………………………………………………2分 ‎∴不等式组的解集是1＜＜3． ……………………………………………………2分 在数轴上表示 ………………………………………………………………………2分 ‎19．（8分）(1) cos∠D=cos∠ABC==0.94， ………………………………… 3分 ‎∴∠D20°． ………………………………………………………………………1分 ‎（2）EF=DEsin∠D=85sin20°85×0.34=28.9(米) ， ……………………………3分 共需台阶28.9×100÷17=170级． ………………………………………………1分 ‎20．（8分）（1）①当0≤≤6时， ………………………………………………………1分 ‎； ………………………………………………………………………………2分 ‎②当6＜≤14时， ……………………………………………………………………1分 设，‎ ‎∵图象过（6，600），（14，0）两点，‎ ‎∴ 解得 ‎ ‎∴． ‎ ‎∴ …………………………………………………………2分 ‎（2）当时，， ……………………………………1分 ‎（千米/小时）． ………………………………………………………1分 ‎21．（10分）（1）画直方图 …………………………………………………………………2分 ‎=10， 相应扇形的圆心角为：360°×10%=36°． ………………………………2分 ‎（2），‎ ‎， …………………………………2分 ‎＞，由样本估计总体的思想，说明通过新技术管理甲地块杨梅产量高于乙地 块杨梅产量． ……………………………………………………………………………1分 ‎（若没说明“由样本估计总体”不扣分）‎ ‎　（3）P=． ………………………………………………………………………3分 ‎22．（12分）（1）{3，1}+{1，2}={4，3}． ……………………………………………2分 y O ‎1‎ ‎1‎ x A B C ‎{1，2}+{3，1}={4，3}． …………………………………………………………………2分 ‎（2）①画图 …………………………………………………2分 ‎ 最后的位置仍是B．……………………………………1分 ‎② 证明：由①知，A（3，1），B(4，3)，C（1，2）‎ ‎∴OC=AB==，OA=BC==，‎ ‎ ∴四边形OABC是平行四边形．…………………………3分 ‎（3）{2，3}+{3，2}+{-5，-5}={0, 0}．……………………2分 ‎23．（12分）（1）① = ………………………………………………………………………2分 ‎② ＞ …………………………………………………………………………………2分 ‎（2）＞………………………………………………………………………………………2分 证明：作点C关于FD的对称点G，‎ 连接GK，GM，GD，‎ 则CD=GD ，GK = CK，∠GDK=∠CDK，‎ ‎∵D是AB的中点，∴AD=CD=GD．‎ ‎∵30°，∴∠CDA=120°，‎ ‎∵∠EDF=60°，∴∠GDM+∠GDK=60°，‎ ‎∠ADM+∠CDK =60°．‎ ‎∴∠ADM=∠GDM，………………………………………………………………………3分 ‎∵DM=DM， ‎ ‎∴△ADM≌△GDM，∴GM=AM．‎ ‎∵GM+GK＞MK，∴AM+CK＞MK．……………………………………………………1分 ‎（3）∠CDF=15°，．…………………………………………………………2分 ‎24．（14分）（1）∵A、D关于点Q成中心对称，HQ⊥AB，‎ ‎∴=90°，HD=HA，‎ ‎∴，…………………………………………………………………………3分 ‎（图1）‎ ‎（图2）‎ ‎∴△DHQ∽△ABC． ……………………………………………………………………1分 ‎（2）①如图1，当时， ‎ ED=，QH=，‎ 此时． …………………………………………3分 当时，最大值．‎ ‎②如图2，当时，‎ ED=，QH=，‎ 此时． …………………………………………2分 当时，最大值．‎ ‎∴y与x之间的函数解析式为 y的最大值是．……………………………………………………………………1分 ‎（3）①如图1，当时，‎ 若DE=DH，∵DH=AH=， DE=，‎ ‎∴=，．‎ 显然ED=EH，HD=HE不可能； ……………………………………………………1分 ‎②如图2，当时，‎ 若DE=DH，=，； …………………………………………1分 若HD=HE，此时点D，E分别与点B，A重合，； ………………………1分 若ED=EH，则△EDH∽△HDA，‎ ‎∴，，． ……………………………………1分 ‎∴当x的值为时，△HDE是等腰三角形.‎ ‎（其他解法相应给分）‎