2012年上海市中考数学试题（含答案） 10页

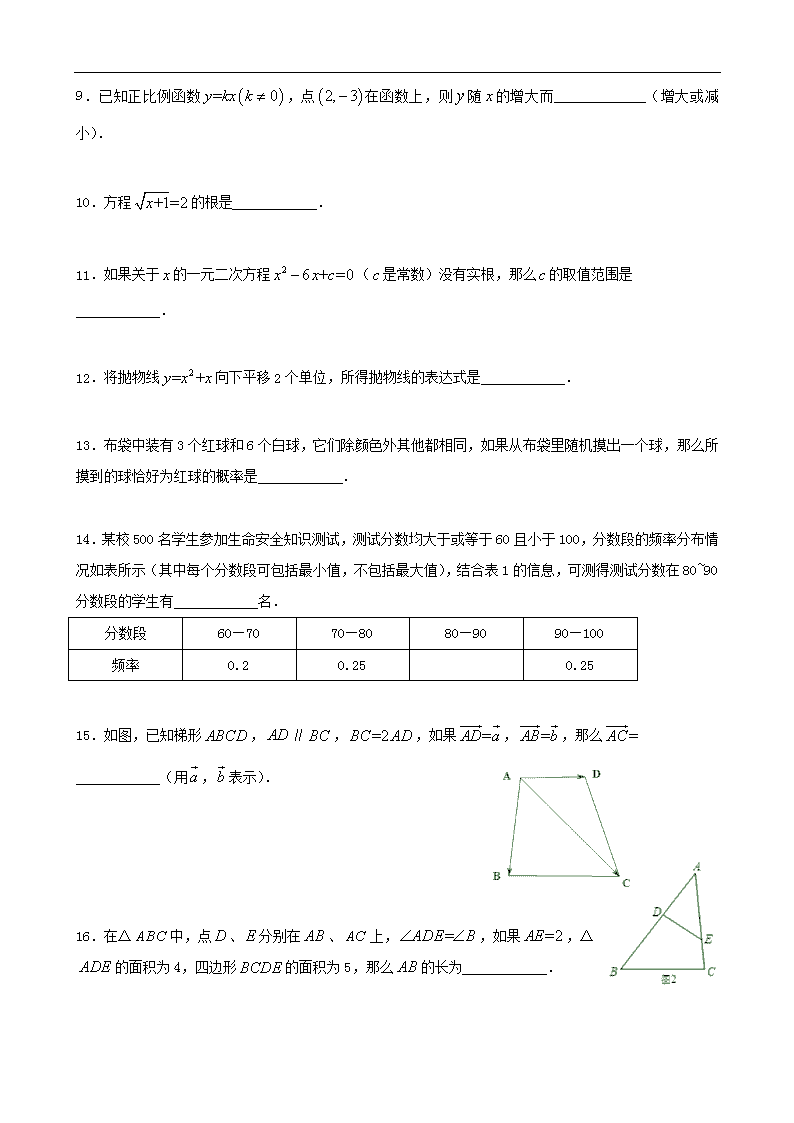
‎2012年上海中考数学试题 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．在下列代数式中，次数为3的单项式是（ ）‎ ‎； ； ．； ．．‎ ‎2数据5,7,5,8,6,13,5的中位数是（ ）‎ ‎．5； ．6； ．7 ； ．8．‎ ‎3．不等式组的解集是（ ）‎ ‎．； ．； ．； ．．‎ ‎4．在下列各式中，二次根式的有理化因式（ ）‎ ‎．； ．； ．； ．．‎ ‎5在下列图形中，为中心对称图形的是（ ）‎ ‎．等腰梯形； ．平行四边形； ．正五边形； ．等腰三角形．‎ ‎6如果两圆的半径长分别为6和2，圆心距为3，那么这两个圆的位置关系是（ ）‎ ‎．外离； ．相切； ．相交； ．内含．‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．计算 ．‎ ‎8．因式分解 ．‎ ‎9．已知正比例函数，点在函数上，则随的增大而 （增大或减小）．‎ ‎10．方程的根是 ．‎ ‎11．如果关于的一元二次方程（是常数）没有实根，那么的取值范围是 ‎ ．‎ ‎12．将抛物线向下平移2个单位，所得抛物线的表达式是 ．‎ ‎13．布袋中装有3个红球和6个白球，它们除颜色外其他都相同，如果从布袋里随机摸出一个球，那么所摸到的球恰好为红球的概率是 ．‎ ‎14．某校500名学生参加生命安全知识测试，测试分数均大于或等于60且小于100，分数段的频率分布情况如表所示（其中每个分数段可包括最小值，不包括最大值），结合表1的信息，可测得测试分数在80~90分数段的学生有 名．‎ 分数段 ‎60—70‎ ‎70—80‎ ‎80—90‎ ‎90—100‎ 频率 ‎0.2‎ ‎0.25‎ ‎0.25‎ ‎15．如图，已知梯形，∥，，如果，，那么 ‎ （用，表示）．‎ ‎16．在△中，点、分别在、上，，如果，△的面积为4，四边形的面积为5，那么的长为 ．‎ ‎17．我们把两个三角形的中心之间的距离叫做重心距，在同一个平面内有两个边长相等的等边三角形，如果当它们的一边重合时，重心距为2，那么当它们的一对角成对顶角时，重心距为 ．‎ ‎18．如图，在△中，，，，点在上，将△沿直线翻折后，将点落在点处，如果，那么线段的长为 ．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ ‎．‎ ‎20．（本题满分10分）‎ 解方程：．‎ ‎21．(本题满分10分，第（1）小题满分4分．第（2）小题满分6分）‎ 如图在△中，∠，是边的中点，⊥，垂足为点．己知，． ‎ ‎（1）求线段的长；‎ ‎（2）求∠的值．‎ ‎22．‎ 某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本（万元/吨）与生产数量（吨）的函数关系式如图所示．‎ ‎（1）求关于的函数解析式，并写出它的定义域；‎ ‎（2）当生产这种产品的总成本为280万元时，求该产品的生产数量．‎ ‎ （注：总成本=每吨的成本×生产数量）‎ ‎23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）‎ 己知：如图，在菱形中，点、分别在边、，∠ =∠，与交于点． ‎ ‎（1）求证：‎ ‎（2）当要=时，求证：四边形是平行四边形．‎ ‎24．（本题满分12分，第（1）小题满分3分，第（2）小题满分5分，第（3）小题满分4分）‎ 如图，在平面直角坐标系中，二次函数的图像经过点、，与轴交于点，点在线段上，，点在第二象限，∠，‎ ‎，，垂足为．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）求线段、的长（用含的代数式表示）；‎ ‎（3）当∠ =∠时，求的值．‎ ‎25．（本题满分14分，第（1）小题满分3分，第（2）小题满分5分，第（3）小题满分6分）‎ 如图，在半径为2的扇形中，∠，点是弧上的一个动点（不与点、重合）⊥，⊥，垂足分别为、．‎ ‎（1）当时，求线段的长；‎ ‎（2）在△中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；‎ ‎（3）设，△的面积为，求关于的函数关系式，并写出它的定义域．‎ ‎ ‎ ‎ 答案 ‎1．．‎ ‎2．．‎ ‎3．．‎ ‎4．．‎ ‎5．． ‎ ‎6．．‎ ‎7．．‎ ‎8． ．‎ ‎9．减小． ‎ ‎10．． ‎ ‎11．． ‎ ‎12．．‎ ‎13．． ‎ ‎14．150． ‎ ‎15．． ‎ ‎16．3． ‎ ‎17．4． ‎ ‎18．．‎ ‎19．3． ‎ 解 ：原式=‎ ‎ =‎ ‎ =3．‎ 20. ‎．．‎ 解：x(x-3)+6=x-3‎ ‎ x-4x+3=0‎ ‎ x1=2或x2=3 ‎ ‎ 经检验:x=3是方程的增根 x=1是原方程的根 ‎21．（或12.5）； ．‎ ‎22．① y=－x+11（10x50)‎ ‎ ② 40．‎ ‎23．‎ ‎ ‎ ‎24．‎ ‎ ‎ ‎25．‎ ‎ ‎ ‎ ‎ ‎ ‎