人教版九年级下册数学导学案 第二十九章 投影与视图 6页

第二十九章 投影与视图 第一课时 投 影 课前自习 1. 同学们，我们几千年前的古人就已经对物体的影子进行了研究和利用，例如河南的皮影戏，古 代人用来计时的日晷（ gui  ）,课本 P101 图。这一节课，我们来学习图形的投影。 2. 用光线照射物体，在某一个平面内形成的影子称为投影，照射光线称为：投影所在的平面称 为： 。 3. 投影分为两种 A：一种是平行光线所成的投影它称为： ，例如：太阳光线下物体所成的影子。 B：还有一种是由同一点发出的光线形成的投影叫做例如放影机的投影，小灯泡发光成的影子， 其实这种投影形成的影子与实物是成位似变换的。当然这一章我们主要学习平行投影中的平行 正投影。 4.正投影是指投影线投影面产生的投影。 练习： P101 练习 5.如图 P102 探究 第一种情况： 当铁丝平行于投影面时，这时，我们可得： 1 1 1 1 1 1 1 1 1 1 / / , AA //BB AA B B AA B B = AB A B AB A B      而光线是平行光线 四边形 是平行四边形 在 中 第二种情况 当铁丝不平行于投影面时，这时，我们可得： 2 2 2 2 2 2 2 AC BB AA B C AC=A B R ACB AB>AC AB(_____)A B t        作 由第一种情况可得： 为平行四边形 又 在 中 第三种情况： 当 AB 的倾斜角慢慢增大，最后和投影面垂直时，这时的正投影就只是一个点了。 6.P103 探究， 对于一个平面图形来讲，也有一种这样的关系，当物体与投影面垂直时，影子和物体是全等的。 例 P104 例题由同学们自学习。 练习 P105 练习题 第一种情况： 这时的正投影形状应该是一个矩形。这个好多同学都明白，但是在画图时，我们需注意，我们画 出的长方形的长应该等于圆柱的长，我们画出的长方形的宽应该等于圆柱的直径。 第二种情况： 此时的投影应是一个圆，注意这个圆的半径应该等于半径。 课后巩固练习： A 组 P105 习题 29.1 第 1、2、3、4、5、6 题。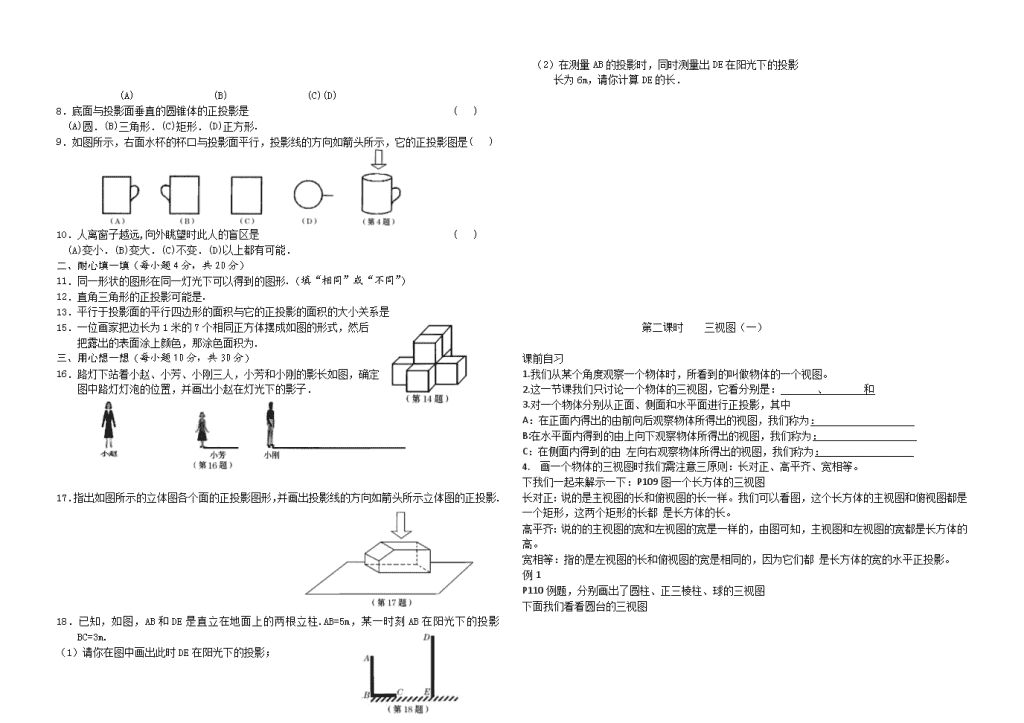 B 组 1．下面四幅图是两个物体不同时刻在太阳光下的影子，按照时间的先后顺序正确的是 ( ) (A)A→B→C→D． (B)D→B→C→A． (C)C→D→A→B． (D)A→C→B→D． 2．球的正投影是 ( ) (A)圆面． (B)椭圆面． (C)点． (D)圆环. 3.在同一时刻，两根长度不等的竿子置于阳光之下，但看到它们的影长相等，那么这两根竿子的相 对位置是 ( ) (A)两竿都垂直于地面． (B)两竿平行斜插在地上． (C)两根竿子不平行． (D)一根竿倒在地上． 4．平行投影中的光线是 ( ) (A)平行的． (B)聚成一点的． (C)不平行的． (D)向四面发散的． 5．两个不同长度的的物体在同一时刻同一地点的太阳光下得到的投影是 ( ) (Ａ)相等．(B)长的较长．(C)短的较长．(D)不能确定． 6．正方形在太阳光的投影下得到的几何图形一定是 ( ) (A)正方形．(B)平行四边形或一条线段．(C)矩形．(D)菱形． 7．下列图中是太阳光下形成的影子是 ( ) (A) (B) (C)(D) 8．底面与投影面垂直的圆锥体的正投影是 ( ) (A)圆．(B)三角形．(C)矩形．(D)正方形. 9．如图所示，右面水杯的杯口与投影面平行，投影线的方向如箭头所示，它的正投影图是( ) 10．人离窗子越远,向外眺望时此人的盲区是 ( ) (A)变小．(B)变大．(C)不变．(D)以上都有可能． 二、耐心填一填（每小题 4 分，共 20 分） 11．同一形状的图形在同一灯光下可以得到的图形.（填“相同”或“不同”） 12．直角三角形的正投影可能是. 13．平行于投影面的平行四边形的面积与它的正投影的面积的大小关系是 15．一位画家把边长为 1 米的 7 个相同正方体摆成如图的形式，然后 把露出的表面涂上颜色，那涂色面积为. 三、用心想一想（每小题 10 分，共 30 分） 16．路灯下站着小赵、小芳、小刚三人，小芳和小刚的影长如图，确定 图中路灯灯泡的位置，并画出小赵在灯光下的影子． 17．指出如图所示的立体图各个面的正投影图形，并画出投影线的方向如箭头所示立体图的正投影. 18．已知，如图，AB 和 DE 是直立在地面上的两根立柱.AB=5m，某一时刻 AB 在阳光下的投影 BC=3m. （1）请你在图中画出此时 DE 在阳光下的投影； （2）在测量 AB 的投影时，同时测量出 DE 在阳光下的投影 长为 6m，请你计算 DE 的长． 第二课时 三视图（一） 课前自习 1.我们从某个角度观察一个物体时，所看到的叫做物体的一个视图。 2.这一节课我们只讨论一个物体的三视图，它看分别是： 、 和 3.对一个物体分别从正面、侧面和水平面进行正投影，其中 A：在正面内得出的由前向后观察物体所得出的视图，我们称为： B:在水平面内得到的由上向下观察物体所得出的视图，我们称为： C：在侧面内得到的由 左向右观察物体所得出的视图，我们称为： 4. 画一个物体的三视图时我们需注意三原则：长对正、高平齐、宽相等。 下我们一起来解示一下：P109 图一个长方体的三视图 长对正：说的是主视图的长和俯视图的长一样。我们可以看图，这个长方体的主视图和俯视图都是 一个矩形，这两个矩形的长都 是长方体的长。 高平齐：说的的主视图的宽和左视图的宽是一样的，由图可知，主视图和左视图的宽都是长方体的 高。 宽相等：指的是左视图的长和俯视图的宽是相同的，因为它们都 是长方体的宽的水平正投影。 例 1 P110 例题，分别画出了圆柱、正三棱柱、球的三视图 下面我们看看圆台的三视图 主视图：形状是左视图：形状是：俯视图形状是： 下面我们可以画出它的三视图，但有一点必须符合三原由、则： 主视图和左视图两个等腰梯形应是全等的。它们的上和下底分别是圆台的上底圆和下底圆直径， 它们的腰应该是圆台的母线长。 俯视图应该两个同心圆，而且大、小圆直径应该的下、上底圆直径一样。 如图： 主视图： 左视图： 俯视图： 请同学们注意：里面的小圆是实线，因为我们从上向下看时能看见这个圆，那如果不能看见但又 是实际存在的呢？那我们就用虚线表示： 例如： 这时虽然还是同一个圆台，但是它的主视图、左视图和俯视图就会变化了如图： 主视图： 左视图： 俯视图： 例 2.P111 例 2、3，这些是组合图形，注意能看见的用实线。不能看见的用虚线。 练习： 请同学们画出下面图形的三视图 主视图： 左视图： 俯视图： 练习： P112 第 1、2、3 题 课后巩固练习： A 组 P116 第 1、2、3、6、7 题 P125 复习题第 1、2、4 题 B 组 1.小琳过 14 周岁生日，父母为她预定的生日蛋糕如图所示，它的主视图应该是 ( ) 2、如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵 住方形空洞的是 ( ) 3、有一实物如图，那么它的主视图是 ( ) 4.如图是正三菱柱，它的主视图正确的是( ) 5、画出如图所示中立体图形的三视图. 6、画出下面实物的三视图： 第三课时 三视图（二） 课前自习 1. 这一节课，我们不仅需要由一个立体图形得出它的三视图，还必须能由一个几何图形的三视图 得出这个几何图形的形状。 例如：P113 例 4、5 练习：P114 练习 2. 要得出一个立体图形的展开图，需要对这个几何体有几个面有所了解，这些面中有些是全等的， 有些不全等例如正四面体、四棱锥等等。 正四面体就是我们说的直三棱锥： 它的展开图为： 下面我们看看三棱柱的展开图： 它是三个矩形+两个全等的三角形 例：P114 例 6 练习：P115 练习 课后巩固练习： A 组 P116 第 4、5、8 题 P125 第 3、5、6、7、8 题 B 组 1、某物体三视图如图，则该物体形状可能是 ( ) (A)长方体． (B)圆锥体． (C)立方体． (D)圆柱体． 2、下图是由一些相同的小正方形构成的几何体的三视图，这些相同的小正方形的个数是( ) (A)4 个． (B)5 个． (C)6 个． (D)7 个． 3、由若干个同样大小的正方体堆积成一个实物，不同侧面观察到如下投影图，则构成该 实物的小正方体个数为 4．一个几何体的三视图如下,那么这个几何体是. 5．如果某物体的三视图如图所示，那么该物体的形状是______． 第 5 题图 6．一空间几何体的三视图如图所示，则这个几何体的表面积是______cm2． 7．如图是一个几何体的主视图和俯视图，求该几何体的体积(取 3.14)．