初中数学竞赛辅导讲义及习题解答 第25讲 辅助圆 5页

1 第二十五讲 辅助圆 在处理平面几何中的许多问题时，常需要借助于圆的性质，问题才得以解决． 而我们需要的圆并不存在(有时题设中没有涉及圆；有时虽然题设涉及圆，但是此圆并 不是我们需要用的圆)，这就需要我们利用已知条件，借助图形把需要的实际存在的圆找出 来，添补辅助圆的常见方法有： 1．利用圆的定义添补辅助圆； 2．作三角形的外接圆； 3．运用四点共圆的判定方法： (1)若一个四边形的一组对角互补，则它的四个顶点共圆． (2)同底同侧张等角的三角形，各顶点共圆． (3)若四边形 ABCD 的对角线相交于 P，且 PA·PC=PB·PD，则它的四个顶点共圆． (4)若四边形 ABCD 的一组对边 AB、DC 的延长线相交于 P，且 PA·PB＝PC·PD，则它 的四个顶点共圆． 【例题求解】 【例 1】如图，直线 AB 和 AC 与⊙O 分别相切于 B、C，P 为圆上一点，P 到 AB、AC 的距 离分别为 4cm、6cm，那么 P 到 BC 的距离为 ． 思路点拨 连 DF，EF，寻找 PD、PE、PF 之间的关系，证明△PDF∽△PFE，而发现 P、D、 B、F 与 P、E、C、F 分别共圆，突破角是解题的关键． 注：圆具有丰富的性质： (1)圆的对称性； (2)等圆或同圆中不同名称量的转化； (3)与圆相关的角； (4)圆中比例线段． 适当发现并添出辅助圆，就为圆的丰富性质的运用创造了条件，由于图形的复杂性， 有时在图中并不需画出圆，可谓“图中无圆，心中有圆”． 【例 2】 如图，若 PA=PB，∠APB=2∠ACB，AC 与 PB 交于点 P，且 PB=4，PD=3，则 AD·DC 等于( ) A．6 B．7 C．12 D．16 思路点拨 作出以 P 点为圆心、PA 长为半径的圆，为相交弦定理的应用创设了条件． 2 注：到一个定点等距离的几个点在同一个圆上，这是利用圆的定义添辅助圆的最基本方法． 【例 3】 如图，在△ABC 中，AB=AC，任意延长 CA 到 P，再延长 AB 到 Q，使 AP=BQ， 求证：△ABC 的外心 O 与 A，P，Q 四点共圆． 思路点拨 先作出△ABC 的外心 O，连 PO、OQ，将问题转化为证明角相等． 【例 4】 如图，P 是⊙O 外一点，PA 切⊙O 于 A，PBC 是⊙O 的割线，AD⊥PO 于 D．求 证： CD PC PD PB  ． 思路点拨 因所证比例线段不是对应边，故不能通过判定△PBD 与△PCD 相似证 明．PA2=PD·PO=PB·PC，B、C、O、D 共圆，这样连 OB，就得多对相似三角形，以此 达到证明的目的． 注：四点共圆既是一类问题，又是平面几何中一个重要的证明方法，它和证明三角形全等和 相似三角形有着同等重要的地位，这是因为，某四点共圆，不但与这四点相联系的条件集中 或转移，而且可直接运．用圆的性质为解题服务． 【例 5】如图，在△ABC 中，高 BE、CF 相交于 H，且∠BHC=135°，G 为△ABC 内的一 点，且 GB=GC，∠BGC＝3∠A，连结 HG，求证：HG 平分∠BHF． 思路点拨 经计算可得∠A=45°，△ABE，△BFH 皆为等腰直角三角形，只需证∠GHB= ∠GHF=22.5°． 由∠BGC=3∠A=135°=∠GHC，得 B、G、H、C 四点共圆，运用圆中角转化灵活的特点 证明． 3 注：许多直线形问题借助辅助圆，常能降低问题的难度，使问题获得简解、巧解或新解． 学力训练 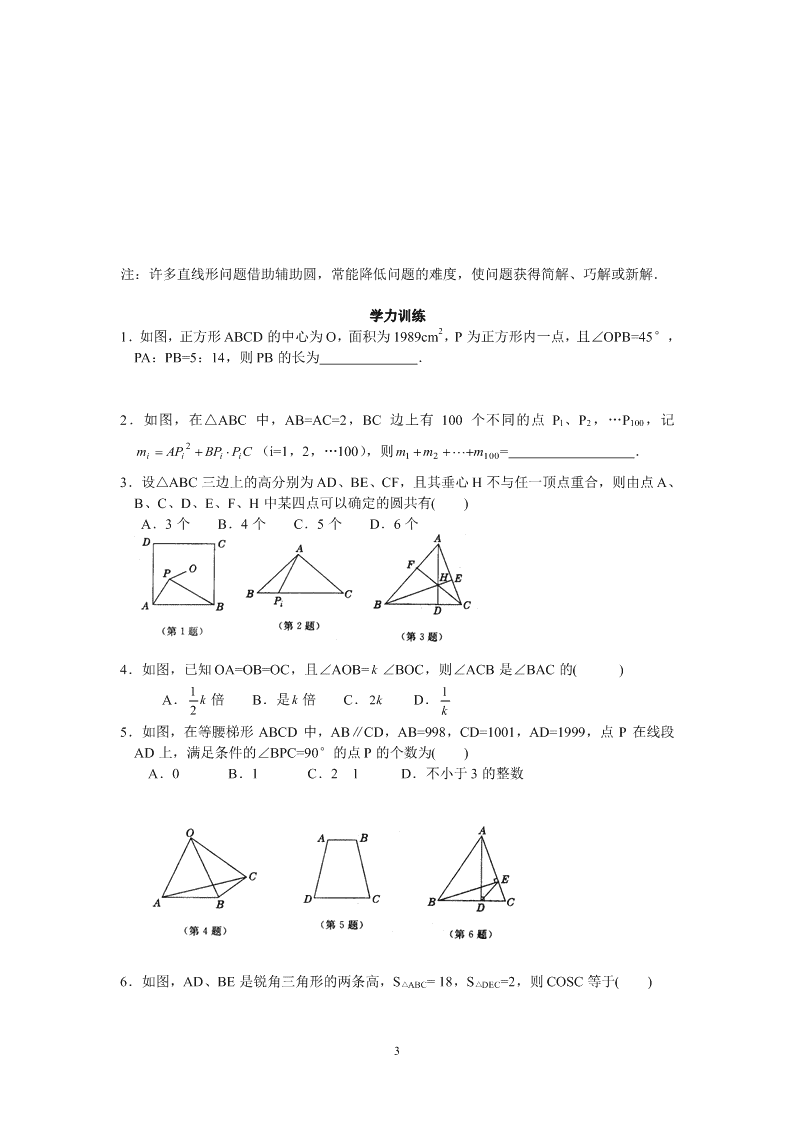1．如图，正方形 ABCD 的中心为 O，面积为 1989cm2，P 为正方形内一点，且∠OPB=45°， PA：PB=5：14，则 PB 的长为 ． 2．如图，在△ABC 中，AB=AC=2，BC 边上有 100 个不同的点 Pl、P2，…P100，记 CPBPAPm iiii  2 （i=1，2，…100），则 10021 mmm   = ． 3．设△ABC 三边上的高分别为 AD、BE、CF，且其垂心 H 不与任一顶点重合，则由点 A、 B、C、D、E、F、H 中某四点可以确定的圆共有( ) A．3 个 B．4 个 C．5 个 D．6 个 4．如图，已知 OA=OB=OC，且∠AOB= k ∠BOC，则∠ACB 是∠BAC 的( ) A． k2 1 倍 B．是 k 倍 C． k2 D． k 1 5．如图，在等腰梯形 ABCD 中，AB∥CD，AB=998，CD=1001，AD=1999，点 P 在线段 AD 上，满足条件的∠BPC=90°的点 P 的个数为( ) A．0 B．1 C．2 1 D．不小于 3 的整数 6．如图，AD、BE 是锐角三角形的两条高，S△ABC= 18，S△DEC=2，则 COSC 等于( ) 4 A．3 B． 3 1 C． 3 2 D． 4 3 7．如图；已知 H 是△ABC 三条高的交点，连结 DF，DE，EF，求证：H 是△DEF 的内心． 8．如图，已知△ABC 中，AH 是高，AT 是角平分线，且 TD⊥AB，TE⊥AC． 求证：(1)∠AHD=∠AHE；(2) CE CH BD BH  9 ． 如 图 ， 已 知 在 凸 四 边 形 ABCDE 中 ， ∠BAE=3  ， BC=CD=DE ，且∠BCD= ∠ CDE= 2180  ．求证：∠BAC=∠CAD=∠DAK， 10．如图，P 是⊙O 外一点，PA 和 PB 是⊙O 的切线，A，B 为切点，P O 与 AB 交于点 M， 过 M 任作⊙O 的弦 CD．求证：∠CPO=∠DPO． 11．如图，已知点 P 是⊙O 外一点，PS、PT 是⊙O 的两条切线，过点 P 作⊙O 的割线 PAB， 交⊙O A、B 两点，与 ST 交于点 C．求证： )11(2 11 PBPAPC  5 参考答案