中考压轴题专题辅助圆的应用 3页

‎ ‎ 辅助圆的应用 ‎【学习目标】1、熟练掌握利用圆构造等腰三角形和直角三角形；‎ ‎ 2、学会在恰当的时候利用圆为辅助线解决实际问题.‎ ‎【重点难点】利用圆为辅助线解决实际问题.‎ ‎【学习过程】‎ 一、 利用“两圆一中垂线”构造等腰三角形 如图，已知抛物线（a≠0）与轴交于点A(1，0)和点B (－3，0)与y轴交于点C．‎ ‎(1)抛物线的解析式为 ；‎ ‎(2) 设抛物线的对称轴与轴交于点M ，问在对称轴上是否存在点P，使△CAP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标．‎ 二、 利用“两垂线一圆”构造直角三角形 如图，已知抛物线（a≠0）与轴交于点A(1，0)和点B (－3，0)，与y轴交于点C．在抛物线的对称轴上是否存在点Q，使△CBQ是直角三角形，若存在，请直接写出所有符合条件的点Q的坐标．‎ 三、 利用圆求线段的最值 ‎1. 如图①，菱形ABCD的边长为2，∠ABC=60°，点E是AD边的中点，F是CD上的动点，将△DEF沿EF折叠，点D落在P处,则线段BP最短时的长度为 .‎ 图②‎ 图①‎ 图③‎ ‎2. 如图②，在Rt△ABC中，∠CAB=90°，AC=AB=1，以AC上动点O为圆心，以AO为半径作圆O，交AC于点D，连接BD交圆O于点E，则CE的最小值为 ‎ ‎3.如图③，⊙O的半径为5，OP=3，经过点P的最长弦为 ，最短弦为 .‎ 四、 三点及三点以上到同一点距离相等，作辅助圆 如图，四边形ABCD中，DC∥AB，BC=2，AB=AC=AD=4．则BD的长为 . 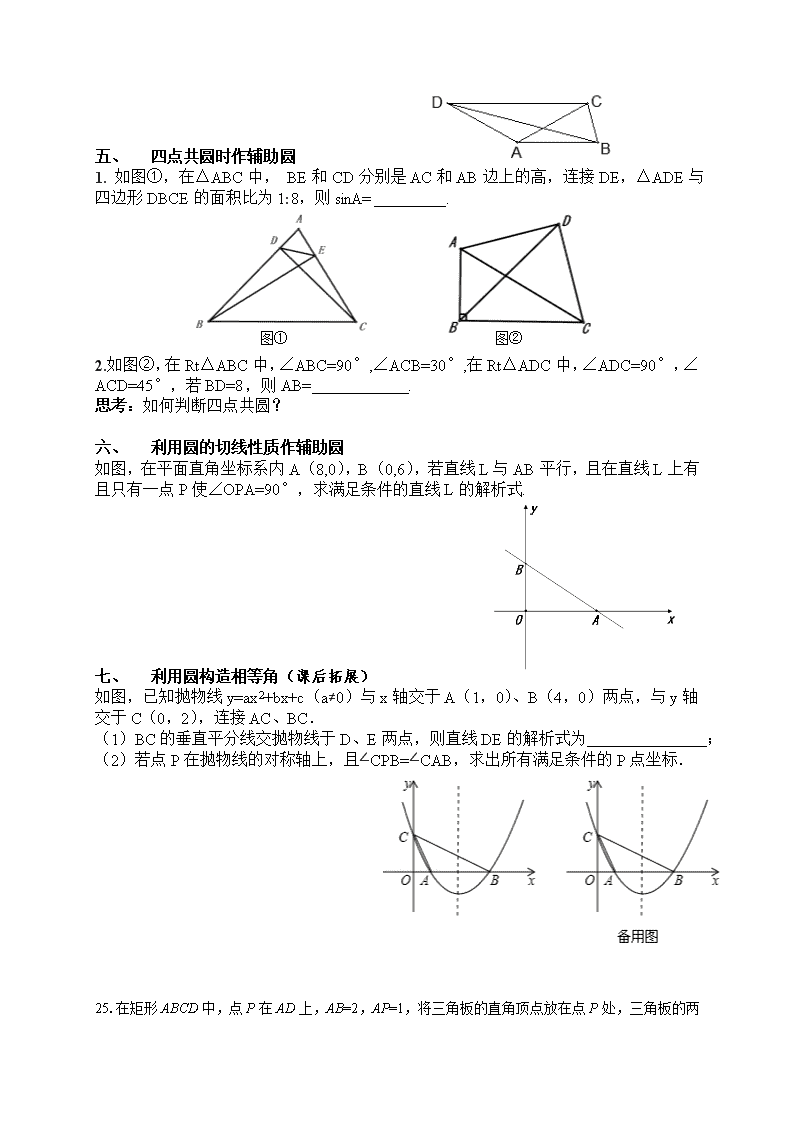‎ 一、 四点共圆时作辅助圆 ‎1. 如图①，在△ABC中， BE和CD分别是AC和AB边上的高，连接DE，△ADE与四边形DBCE的面积比为1:8，则sinA= .‎ 图①‎ 图②‎ ‎2.如图②，在Rt△ABC中，∠ABC=90°,∠ACB=30°,在Rt△ADC中，∠ADC=90°，∠ACD=45°，若BD=8，则AB= .‎ 思考：如何判断四点共圆？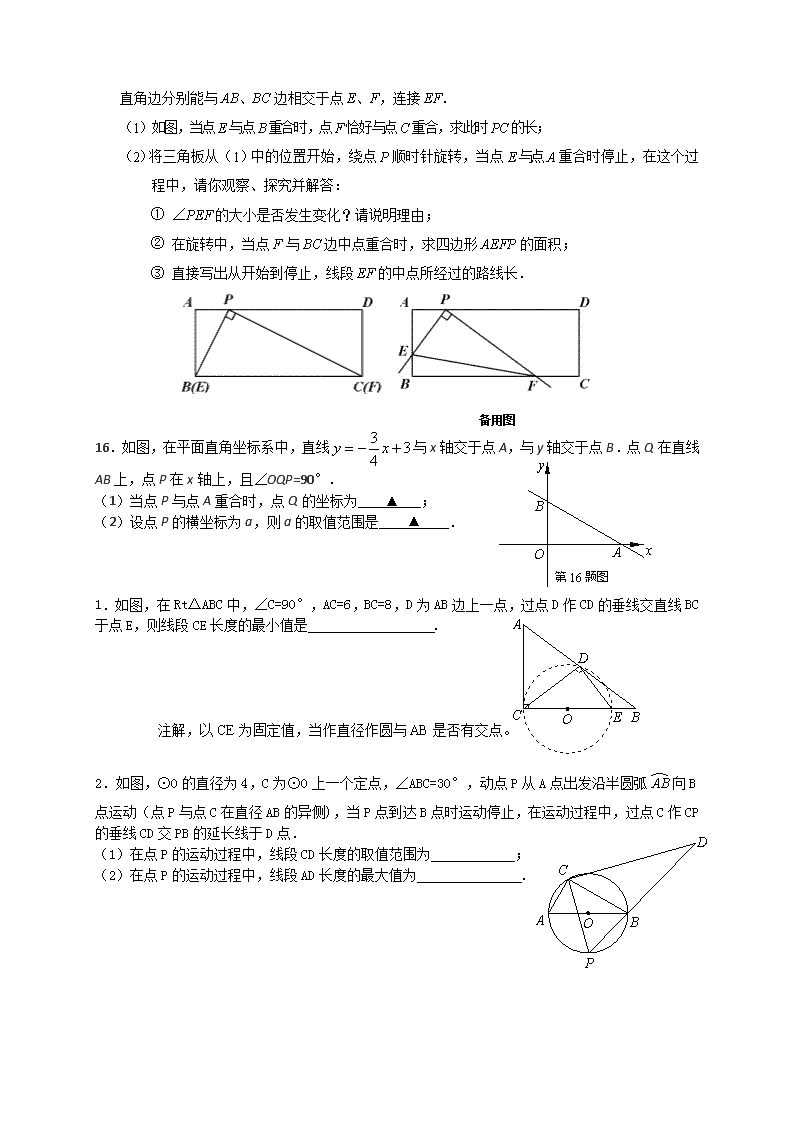‎ 二、 利用圆的切线性质作辅助圆 如图，在平面直角坐标系内A（8,0），B（0,6），若直线L与AB平行，且在直线L上有且只有一点P使∠OPA=90°，求满足条件的直线L的解析式.‎ 三、 利用圆构造相等角（课后拓展）‎ 如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于A（1，0）、B（4，0）两点，与y轴交于C（0，2），连接AC、BC．‎ ‎（1）BC的垂直平分线交抛物线于D、E两点，则直线DE的解析式为 ；‎ ‎（2）若点P在抛物线的对称轴上，且∠CPB=∠CAB，求出所有满足条件的P点坐标．‎ ‎25. 在矩形ABCD中，点P在AD上，AB=2，AP=1，将三角板的直角顶点放在点P 处，三角板的两直角边分别能与AB、BC边相交于点E、F，连接EF．‎ ‎（1）如图，当点E与点B重合时，点F恰好与点C重合，求此时PC的长；‎ ‎（2）将三角板从（1）中的位置开始，绕点P顺时针旋转，当点E与点A重合时停止，在这个过程中，请你观察、探究并解答：‎ ‎① ∠PEF的大小是否发生变化？请说明理由；‎ ‎② 在旋转中，当点F与BC边中点重合时，求四边形AEFP的面积；‎ ‎③ 直接写出从开始到停止，线段EF的中点所经过的路线长．‎ 备用图 O A B y x 第16题图 ‎16．如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B．点Q在直线AB上，点P在x轴上，且∠OQP=90°．‎ ‎（1）当点P与点A重合时，点Q的坐标为 ▲ ；‎ ‎（2）设点P的横坐标为a，则a的取值范围是 ▲ ．‎ ‎1．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，D为AB边上一点，过点D作CD的垂线交直线BC于点E，则线段CE长度的最小值是 .‎ 注解，以CE为固定值，当作直径作圆与AB是否有交点。‎ ‎2．如图，⊙O的直径为4，C为⊙O上一个定点，∠ABC=30°，动点P从A点出发沿半圆弧向B点运动（点P与点C在直径AB的异侧)，当P点到达B点时运动停止，在运动过程中，过点C作CP的垂线CD交PB的延长线于D点．‎ ‎（1）在点P的运动过程中，线段CD长度的取值范围为 ；‎ ‎（2）在点P的运动过程中，线段AD长度的最大值为 .‎ ‎ ‎