嘉兴市中考数学试卷含答案解析 24页

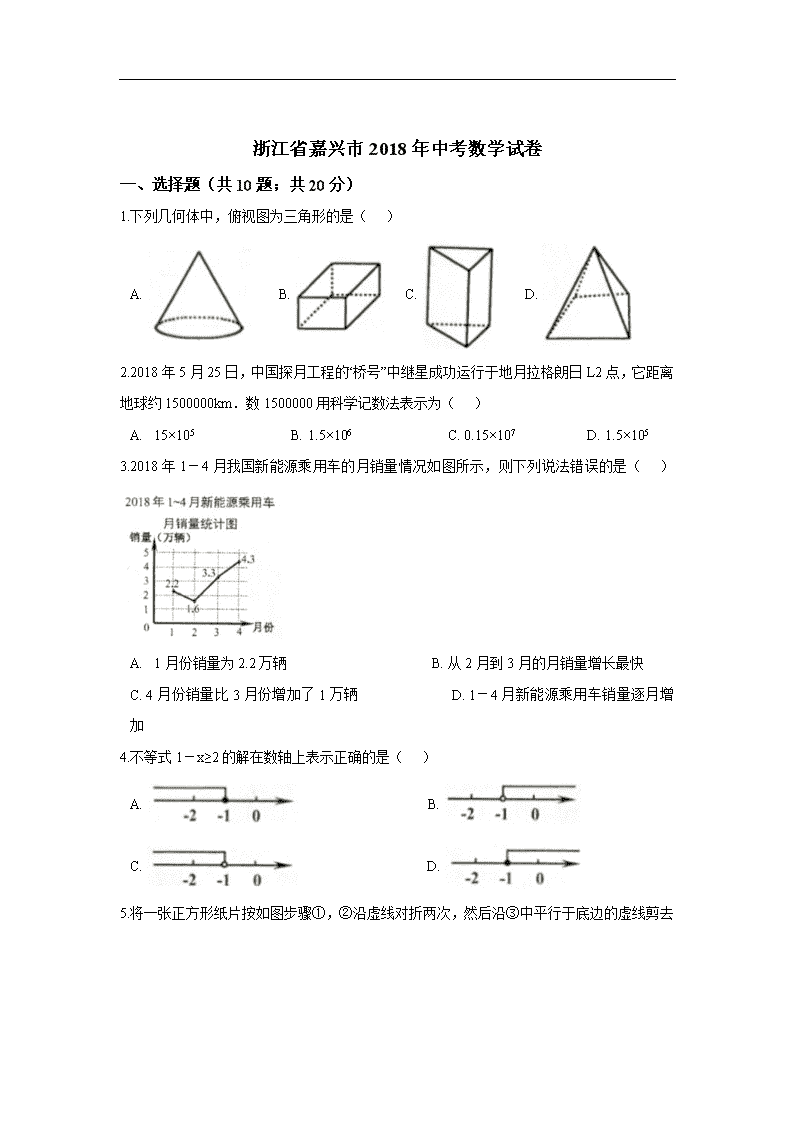
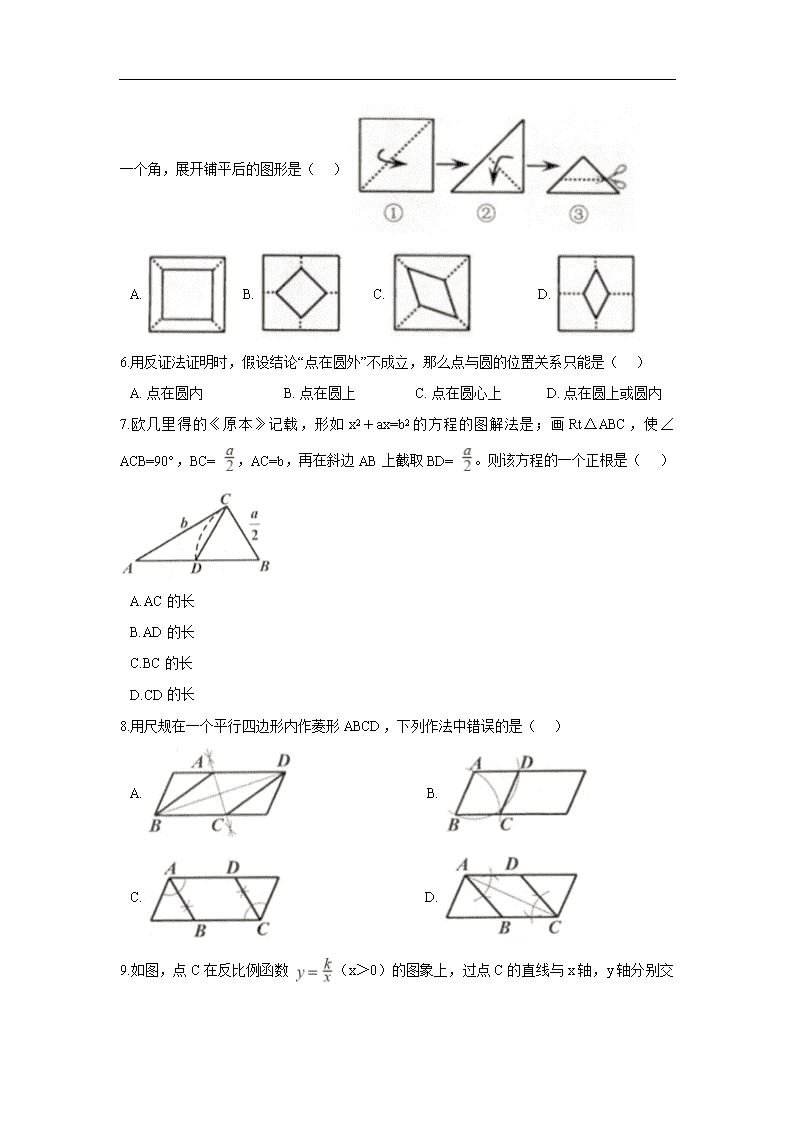
浙江省嘉兴市 2018 年中考数学试卷 一、选择题（共 10 题；共 20 分） 1.下列几何体中，俯视图为三角形的是（ ） A. B. C. D. 2.2018 年 5 月 25 日，中国探月工程的“桥号”中继星成功运行于地月拉格朗日 L2 点，它距离 地球约 1500000km．数 1500000 用科学记数法表示为（ ） A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105 3.2018 年 1－4 月我国新能源乘用车的月销量情况如图所示，则下列说法错误的是（ ） A. 1 月份销量为 2.2 万辆 B. 从 2 月到 3 月的月销量增长最快 C. 4 月份销量比 3 月份增加了 1 万辆 D. 1－4 月新能源乘用车销量逐月增 加 4.不等式 1－x≥2 的解在数轴上表示正确的是（ ） A. B. C. D. 5.将一张正方形纸片按如图步骤①，②沿虚线对折两次，然后沿③中平行于底边的虚线剪去 一个角，展开铺平后的图形是（ ） A. B. C. D. 6.用反证法证明时，假设结论“点在圆外”不成立，那么点与圆的位置关系只能是（ ） A. 点在圆内 B. 点在圆上 C. 点在圆心上 D. 点在圆上或圆内 7.欧几里得的《原本》记载，形如 x2＋ax=b2 的方程的图解法是；画 Rt△ABC，使∠ ACB=90°，BC= ，AC=b，再在斜边 AB 上截取 BD= 。则该方程的一个正根是（ ） A.AC 的长 B.AD 的长 C.BC 的长 D.CD 的长 8.用尺规在一个平行四边形内作菱形 ABCD，下列作法中错误的是（ ） A. B. C. D. 9.如图，点 C 在反比例函数 （x＞0）的图象上，过点 C 的直线与 x 轴，y 轴分别交 于点 A，B，且 AB=BC，△AOB 的面积为 1，则 k 的值为（ ） A. 1 B. 2 C. 3 D. 4 10.某届世界杯的小组比赛规则：四个球队进行单循环比赛（每两队赛一场），胜一场得 3 分，平一场得 1 分，负一场得 0 分，某小组比赛结束后，甲、乙，丙、丁四队分别获得第一， 二，三，四名，各队的总得分恰好是四个连续奇数，则与乙打平的球队是（ ） A.甲 B.甲与丁 C.丙 D.丙与丁 二、填空题（共 6 题；共 7 分） 11.分解因式 m2-3m=________。 12.如图，直线 l1∥l2∥l3 ， 直线 AC 交 l1 ， l2 ， l3 ， 于点 A，B，C；直线 DF 交 l1 ， l2 ， l3 于点 D，E，F，已知 ，则 =________。 13.小明和小红玩抛硬币游戏，连续抛两次，小明说：“如果两次都是正面，那么你赢；如果 两次是一正一反，则我赢，”小红赢的概率是________，据此判断该游戏________（填“公平” 或“不公平”）。 14.如图，量角器的 0 度刻度线为 AB，将一矩形直尺与量角器部分重叠，使直尺一边与量角 器相切于点 C，直尺另一边交量角器于点 A，D，量得 AD=10cm，点 D 在量角器上的读数 为 60°，则该直尺的宽度为________ cm。 15.甲、乙两个机器人检测零件，甲比乙每小时多检测 20 个，甲检测 300 个比乙检测 200 个 所用的时间少 10％，若设甲每小时检 x 个，则根据题意，可列处方程：________。 16.如图，在矩形 ABCD 中，AB=4，AD=2，点 E 在 CD 上，DE=1，点 F 是边 AB 上一动点， 以 EF 为斜边作 Rt△EFP．若点 P 在矩形 ABCD 的边上，且这样的直角三角形恰好有两个， 则 AF 的值是________。 三、解答题（共 8 题；共 90 分） 17. （1）计算：2（ －1）＋|-3|-（ -1）0； （2）化简并求值 ，其中 a=1，b=2。 18. 用 消 元 法 解 方 程 组 时 ， 两 位 同 学 的 解 法 如 下 ： （1）反思：上述两个解题过程中有无计算错误？若有误，请在错误处打“×”。 （2）请选择一种你喜欢的方法，完成解答。 19.已知：在△ABC 中，AB=AC，D 为 AC 的中点，DE⊥AB，DF⊥BC，垂足分别为点 E， F，且 DE=DF。 求证：△ABC 是等边三角形。 20.某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为 176mm-185mm 的产品为合格），随机各轴取了 20 个样品进行测，过程如下：收集数据（单位：mm）： 甲车间：168，175，180，185，172，189，185，182，185，174，192，180，185，178， 173，185，169，187，176，180。 乙车间：186，180，189，183，176，173，178，167，180，175，178，182，180，179， 185，180，184，182，180，183。 整理数据： 分析数据： 应用数据： （1）计算甲车间样品的合格率。 （2）估计乙车间生产的 1000 个该款新产品中合格产品有多少个？ （3）结合上述数据信息，请判断个车间生产的新产品更好，并说明理由， 21.小红帮弟弟荡秋千（如图 1），秋千离地面的高度 h（m）与动时间 t（s）之间的关系如 图 2 所示。 （1）根据函数的定义，请判断变量 h 是否为关于 t 的函数？ （2）结合图象回答：①当 t=0.7s 时，h 的值是多少？并说明它的实际意义， ②秋千摆动第一个来回需多少时间？ 22.如图 1，滑动调节式遮阳伞的立柱 AC 垂直于地面 AB，P 为立柱上的滑动调节点，伞体 的截面示意图为△PDE，F 为 PD 中点，AC=2.8m，PD=2m，CF=1m，∠DPE=20°。当点 P 位于初始位置 P0 时，点 D 与 C 重合（图 2），根据生活经验，当太阳光线与 PE 垂直时， 遮阳效果最佳。 （1）上午 10：00 时，太阳光线与地面的夹角为 65°（图 3），为使遮阳效果最佳，点 P 需 从 P0 上调多少距离？（结果精确到 0.1m） （2）中午 12：00 时，太阳光线与地面垂直（图 4），为使遮阳效果最佳，点 P 在（1）的 基础上还需上调多少距离？（结果精确到 0.1m）（参考数：sin70°≈0.94，cos70°≈0.34， tan70°≈2.75， ≈1.41， ≈1.73） 23.已知，点 M 为二次函数 y=-（x-b）2＋4b＋1 图象的顶点，直线 y=mx＋5 分别交 x 轴正半 轴，y 轴于点 A，B。 （1）判断顶点 M 是否在直线 y=4x＋1 上，并说明理由。 （2）如图 1，若二次函数图象也经过点 A，B，且 mx＋5＞-（x-b）2＋4b＋1，根据图象， 写出 x 的取值范围。 （3）如图 2，点 A 坐标为（5，0），点 M 在△AOB 内，若点 C（ ，y1），D（ ，y2） 都在二次函数图象上，试比较 y1 与 y2 的大小。 24.我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三 角形，这条边叫做这个三角形的“等底”。 （1）概念理解：如图 1，在△ABC 中，AC=6，BC=3，∠ACB=30°，试判断△ABC 是否是 “等高底”三角形请说明理由。 （2）问题探究：如图 2，△ABC 是“等高底”三角形，BC 是“等底”，作△ABC 关于 BC 所 在直线的对称图形得到△A'BC，连结 AA'交直线 BC 于点 D．若点 B 是△AA'C 的重心，求 的值． （3）应用拓展：如图 3．已知 l1∥l2 ， l1 与 l2 之间的距离为 2．“等高底”△ABC 的“等底”BC 在直线 l1 上，点 A 在直线 l2 上，有一边的长是 BC 的 倍．将△ABC 绕点 C 按顺时针方 向旋转 45°得到△A'B'C，AC 所在直线交 l2 于点 D．求 CD 的值。 答案解析部分 一、选择题 1.【答案】C 【考点】简单几何体的三视图 【解析】【解答】Ａ、圆锥的俯视图是一个圆并用圆心，故Ａ不符合题意； Ｂ、长方体的俯视图是一个长方形，故Ｂ不符合题意； Ｃ、直三棱柱的俯视图是三角形，故Ｃ符合题意； Ｄ、四棱锥的俯视图是一个四边形，故Ｄ不符合题意； 故答案为 C。 【分析】俯视图指的是在水平投影面上的正投影，通俗的讲是从上面往下面看到的图形． 2.【答案】B 【考点】科学记数法—表示绝对值较大的数 【解析】【解答】解：1500000=1.5×1000000=1.5×106 故答案为 B。 【分析】考查用科学记数表示绝对值较大的数，将数表示形 a×10n ， 其中 1≤|a|<10，n 是 正整数． 3.【答案】D 【考点】折线统计图 【解析】【解答】解：A、显然正确，故 A 不符合题意； B、2 月份到 3 月份的线段最陡，所以 2 月到 3 月的月销量增长最快，说法正确，故 B 不符 合题意； C、4 月份销量为 4.3 万辆，3 月份销量为 3.3 万量，4.3-3.3=1（万辆），说法正确，故不符 合题意； D、1 月到 2 月是减少的，说法错误，故 D 符合题意； 故答案为 D 【分析】A、正确读取 1 月份的数据，即可知；B、根据折线统计图看增长快慢，只需要看 各线段的陡的程度，线段越陡，则越快；C、正确读取 4 月、3 月的数据，即可知；D、观 察折线的趋势，逐月增加的应该是上升的折线，而图中有下降。 4.【答案】A 【考点】解一元一次不等式 【解析】【解答】解：因为 1－x≥2，3≥x， 所以不等式的解为 x≤3， 故答案为 A。 【分析】解在不等式的解，并在数轴上表示，不等号是“≥”或“≤”的时候，点要打实心 5.【答案】A 【考点】剪纸问题 【解析】【解答】解：沿虚线剪开以后，剩下的图形先向右上方展开，缺失的部分是一个等 腰直角三角形，用直角边与正方形的边是分别平行的，再沿着对角线展开，得到图形 A。 故答案为 A。 【分析】根据对称的性质，用倒推法去展开这个折纸。 6.【答案】D 【考点】点与圆的位置关系，反证法 【解析】【解答】解：点与圆的位置关系只有三种：点在圆内、点在圆上、点在圆外， 如果点不在圆外，那么点就有可能在圆上或圆内 故答案为 D 【分析】运用反证法证明，第一步就要假设结论不成立，即结论的反面，要考虑到反面所有 的情况。 7.【答案】B 【考点】一元二次方程的根，勾股定理 【解析】【解答】解：在 Rt△ABC 中，由勾股定理可得 AC2+BC2=AB2=（AD+BD）2 ， 因为 AC=b，BD=BC= ， 所以 b2+ = ， 整理可得 AD2+aAD=b2 ， 与方程 x2＋ax=b2 相同， 因为 AD 的长度是正数，所以 AD 是 x2＋ax=b2 的一个正根 故答案为 B。 【分析】由勾股定理不难得到 AC2+BC2=AB2=（AD+BD）2 ， 代入 b 和 a 即可得到答案 8.【答案】C 【考点】平行四边形的性质，菱形的判定，作图—尺规作图的定义 【解析】【解答】解：A、作的辅助线 AC 是 BD 的垂直平分线，由平行四边形中心对称图 形的性质可得 AC 与 BD 互相平分且垂直，则四边形 ABCD 是菱形，故 A 不符合题意； B、由辅助线可得 AD=AB=BC，由平行四边形的性质可得 AD//BC，则四边形 ABCD 是菱 形，故 B 不符合题意； C、辅助线 AB、CD 分别是原平行四边形一组对角的角平分线，只能说明四边形 ABCD 是 平行四边形，故 C 符合题意； D、此题的作法是：连接 AC，分别作两个角与已知角∠CAD、∠ACB 相等的角，即∠BAC= ∠DAC，∠ACB=∠ACD， 由 AD//BC，得∠BAD+∠ABC=180°， ∠BAC=∠DAC=∠ACB=∠ACD， 则 AB=BC，AD =CD,∠BAD=∠BCD， 则∠BCD+∠ABC=180°， 则 AB//CD， 则四边形 ABCD 是菱形 故 D 不符合题意； 故答案为 C 【分析】首先要理解每个图的作法，作的辅助线所具有的性质，再根据平行四边形的性质和 菱形的判定定理判定 9.【答案】D 【考点】反比例函数系数 k 的几何意义 【解析】【解答】解：过点 C 作 CD 垂直于 y 轴，垂足为 D，作 CE 垂直于 x 轴，垂足为 E，则∠AOB=∠CDB=∠CEA=90° 又因为 AB=BC，∠ABO=∠CBD， 所以△ABO≅△CBD， 所以 S△CBD=S△ABO=1， 因为∠CDB=∠CEA=90°，∠BAO=∠CAE, 所以△ABO~△ACE， 所以 ，则 S△ACE=4， 所以 S 矩形 ODCE=S△CBD+S 四边形 OBCE=S△ACE=4， 则 k=4， 故答案为 D 【分析】根据反比例函数 k 的几何意义，可过 C 点作 CD 垂直于 y 轴，垂足为 D，作 CE 垂 直于 x 轴，垂足为 E，即求矩形 ODCE 的面积 10.【答案】B 【考点】推理与论证 【解析】【解答】解：小组赛一共需要比赛 场， 由分析可知甲是最高分，且可能是 9 或 7 分， 当甲是 9 分时，乙、丙、丁分别是 7 分、5 分、3 分， 因为比赛一场最高得分 3 分， 所以 4 个队的总分最多是 6×3=18 分， 而 9+7+5+3>18，故不符合； 当甲是 7 分时，乙、丙、丁分别是 5 分、3 分、1 分，7+5+3+1<18，符合题意， 因为每人要参加 3 场比赛， 所以甲是 2 胜一平，乙是 1 胜 2 平，丁是 1 平 2 负， 则甲胜丁 1 次，胜丙 1 次，与乙打平 1 次， 因为丙是 3 分，所以丙只能是 1 胜 2 负， 乙另外一次打平是与丁， 则与乙打平的是甲、丁 故答案是 B。 【分析】需要推理出甲、乙、丙、丁四人的分数：每个人都要比赛 3 场，要是 3 场全胜得最 高 9 分，根据已知“甲、乙，丙、丁四队分别获得第一，二，三，四名”和“各队的总得分恰 好是四个连续奇数”，可推理出四人的分数各是多少，再根据胜、平、负一场的分数去讨论 打平的场数。 二、填空题 11.【答案】m（m-3） 【考点】提公因式法因式分解 【解析】【解答】解：原式=m2-3m=m·m-3·m=m(m-3) 故答案为 m（m-3） 【分析】提取公因式 m 即可 12.【答案】2 【考点】平行线分线段成比例 【解析】【解答】解：由 和 BC=AC-AB， 则 , 因为直线 l1∥l2∥l3 ， 所以 =2 故答案为 2 【分析】由 和 BC=AC-AB，可得 的值；由平行线间所夹线段对应成比例可得 13.【答案】 ；不公平 【考点】游戏公平性，概率公式 【解析】【解答】解：抛硬币连续抛两次可能的情况：（正面，正面），（正面，反面）， （反面，正面），（反面，反面），一共有 4 种， 而两次都是正面的只有一次，则 P（两次都是正面）= < 所以该游戏是不公平的。 故答案为 ；不公平 【分析】可列举抛硬币连续抛两次可能的情况，得出两次都是正面的情况数，可求得小红赢 的概率；游戏的公平是双方赢的概率都是 14.【答案】 【考点】垂径定理，切线的性质 【解析】【解答】解：如图，连结 OD，OC，OC 与 AD 交于点 G,设直尺另一边为 EF， 因为点 D 在量角器上的读数为 60°， 所以∠AOD=120°， 因为直尺一边 EF 与量角器相切于点 C， 所以 OC⊥EF， 因为 EF//AD， 所以 OC⊥AD， 由垂径定理得 AG=DG= AD=5 cm，∠AOG= ∠AOD=60°， 在 Rt△AOG 中，AG=5 cm，∠AOG=60°， 则 OG= cm,OC=OA= cm 则 CG=OC-OG= cm. 【分析】因为直尺另一边 EF 与圆 O 相切于点 C，连接 OC，可知求直尺的宽度就是求 CG=OC-OG，而 OC=OA；OG 和 OA 都在 Rt△AOG 中，即根据解直角三角形的思路去做： 由垂定理可知 AG=DG= AD=5cm，∠AOG= ∠AOD=60°，从而可求答案。 15.【答案】 【考点】列分式方程 【解析】【解答】解：设甲每小时检 x 个，则乙每小时检测（x-20）个， 甲检测 300 个的时间为 , 乙检测 200 个所用的时间为 由等量关系可得 故答案为 【分析】根据实际问题列方程，找出列方程的等量关系式：甲检测 300 个的时间=乙检测 200 个所用的时间×（1-10%），分别用未知数 x 表示出各自的时间即可 16.【答案】0 或 1＜AF＜ 或 4 【考点】矩形的性质，圆周角定理，切线的性质，直角三角形的性质 【解析】【解答】解：以 EF 为斜边的直角三角形的直角顶点 P 是以 EF 为直径的圆与矩形 边的交点，取 EF 的中点 O， （1）如图 1，当圆 O 与 AD 相切于点 G 时，连结 OG，此时点 G 与点 P 重合，只有一个点， 此时 AF=OG=DE=1； （2）如图 2，当圆 O 与 BC 相切于点 G，连结 OG，EG，FG，此时有三个点 P 可以构成 Rt △EFP， ∵OG 是圆 O 的切线， ∴OG⊥BC ∴OG//AB//CD ∵OE=OF， ∴BG=CG， ∴OG= （BF+CE）， 设 AF=x，则 BF=4-x，OG= (4-x+4-1)= (7-x)， 则 EF=2OG=7-x，EG2=EC2+CG2=9+1=10,FG2=BG2+BF2=1+(4-x)2 在 Rt△EFG 中，由勾股定理得 EF2=EG2+FG2 ， 得（7-x）2=10+1+（4-x）2,解得 x= 所以当 1＜AF＜ 时，以 EF 为直径的圆与矩形 ABCD 的交点（除了点 E 和 F）只有两个； （3）因为点 F 是边 AB 上一动点： 当点 F 与 A 点重合时，AF=0，此时 Rt△EFP 正好有两个符合题意； 当点 F 与 B 点重合时，AF=4，此时 Rt△EFP 正好有两个符合题意； 故答案为 0 或 1＜AF＜ 或 4 【分析】学习了圆周角的推论：直径所对的圆周角是直角，可提供解题思路，不妨以 EF 为 直径作圆，以边界值去讨论该圆与矩形 ABCD 交点的个数 三、解答题 17.【答案】（1）原式=4 -2+3-1=4 （2）原式= =a-b 当 a=1，b=2 时，原式=1-2=-1 【考点】实数的运算，利用分式运算化简求值 【解析】【分析】（1）按照实数的运算法则计算即可； （2）分式的化简当中，可先运算括号里的，或都运用乘法分配律计算都可 18.【答案】（1）解法一中的计算有误（标记略） （2）由①-②，得-3x=3，解得 x=-1， 把 x=-1 代入①，得-1-3y=5，解得 y=-2， 所以原方程组的解是 【考点】解二元一次方程组 【解析】【分析】（1）解法一运用的是加减消元法，要注意用①-②，即用方程①左边和右 边的式子分别减去方程②左边和右边的式子； （2）解法二运用整体代入的方法达到消元的目的 19.【答案】∵AB=AC， ∴∠B=∠C． ∵DE⊥AB，DF⊥BC ∴∠DEA=∠DFC=Rt∠ ∴D 为 AC 的中点， ∴DA=DC 又∴DF=DF ∴Rt△ADE≌Rt△CDF（HL） ∴∠A=∠C． ∴∠A=∠B=∠C． ∴△ABC 是等边三角形． 【考点】全等三角形的判定与性质，等腰三角形的性质，等边三角形的判定 【解析】【分析】根据 AB=AC，可得出∠B=∠C．根据垂直的定义，可证得∠DEA=∠ DFC，根据中点的定义可得出 DA=DC，即可证明 Rt△ADE≌Rt△CDF，就可得出∠A=∠ C．从而可证得∠A=∠B=∠C，即可求证结论。 20.【答案】（1）甲车间样品的合格率为 ×100％=55％ （2）∵乙车间样品的合格产品数为 20-（1＋2＋2）=15（个）， ∴乙车间样品的合格率为 ×100％=75％。 ∴乙车间的合格产品数为 1000×75％=750（个）． （3）①从样品合格率看，乙车间合格率比甲车间高，所以乙车间生产的新产品更好。②从 样品的方差看，甲、乙平均数相等，且均在合格范围内，而乙的方差小于甲的方差，说明乙 比甲稳定，所以乙车间生产的新产品更好． 【考点】数据分析 【解析】【分析】（1）由题意可知，合格的产品的条件为尺寸范围为 176mm-185mm 的产 品，所以甲车间合格的产品数是（5+6），再除总个数即可； （2）需要先求出乙车间的产品的合格率；而合格产品数（a+b）的值除了可以样品数据中里 数出来，也可以由 20-（1＋2＋2）得到； （3）分析数据中的表格提供了甲、乙车间的平均数、众数、中位数和方差数据，根据它们 的特点结合数据的大小进行比较及评价即可 21.【答案】（1）∵对于每一个摆动时间 t，都有一个唯一的 h 的值与其对应， ∴变量 h 是关于 t 的函数。 （2）①h=0.5m，它的实际意义是秋千摆动 0.7s 时，离地面的高度为 0.5m ②2.8s． 【考点】函数的概念，函数值 【解析】【分析】（1）从函数的定义出发：一般地，在某个变化过程中，设有两个变量 x， y，如果对于 x 的每个确定的值，y 都有唯一确定的值，那么就说 y 是 x 的函数，x 是自变量。 h 是否为关于 t 的函数：即表示 t 为自变量时，每一个 t 的值是否只对应唯一一个 h 的值， 从函数的图象中即可得到答案； （2）①结合实际我们知道在 t=0 的时刻，秋千离地面最高；t=0.7 的时刻，观察该点的纵坐 标 h 的值即可；结合 h 表示高度的实际意义说明即可； ②结合荡秋千的经验，秋千先从一端的最高点下落到最低点，再荡到另一端的最高点，再返 回到最低点，最后回到开始的一端，符合这一过程的即是 0~2.8s。 22.【答案】（1）如图 2，当点 P 位于初始位置 P0 时，CP0=2m。 如图 3，10：00 时，太阳光线与地面的夹角为 65°，点 P 上调至 P1 处， ∠1=90°，∠CAB=90°， ∴∠AP1E=115°， ∴∠CPE=65°． ∵∠DP1E=20°， ∴∠CP1F=45° ∵CF=P1F=1m， ∴∠C=∠CP1F=45°， ∴△CP1F 为等腰直角三角形， ∴CP1= m， P0P1=CP0-CP1=2- ≈0.6m， 即点 P 需从 P0 上调 0.6m （2）如图 4，中午 12：00 时，太阳光线与 PE，地面都垂直，点 P 上调至 P2 处， ∴P2E∥AB ∵∠CAB=90°， ∴∠CP2E=90° ∵∠DP2E=20°， ∴∠CP2F=∠CP2E-∠DP2E=70° ∵CF=P2F=1m，得△CP2F 为等腰三角形， ∴∠C=∠CP2F=70 过点 F 作 FG⊥CP2 于点 G， ∴GP2=P2F·cos70°=1×0.34=0.34m ∴CP2=2GP2=0.68m， ∴P1P2=CP1-CP2= -0.68≈0.7 即点 P 在（1）的基础上还需上调 0.7m。 【考点】等腰三角形的判定与性质，解直角三角形 【解析】【分析】（1）求 P 上升的高度，设上升后的点 P 为 P1 ， 即求 P0P1=CP0-CP1 的 值，其中 CP0=2，即求 CP1 的长度，由已知可得 P1F=CF=1，且可已知求出∠C=45°，从而可 得△CP1F 为等腰直角三角形，由勾股定理求出 CP1 即可； （2）与（1）同理即求 CP2 的长度，因为△CP1F 为等腰三角形，由三线合一定理，作底中 的垂线，根据解直角三角形的方法求出底边的长即可 23.【答案】（1）∵点 M 坐标是（b，4b＋1）， ∴把 x=b 代入 y=4x＋1，得 y=4b＋1， ∴点 M 在直线 y=4x＋1 上。 （2）如图 1，∵直线 y=mx＋5 与 y 轴交于点为 B， ∴点 B 坐标为（0，5） 又∵B（0，5）在抛物线上， ∴5=-（0-b）2＋4b＋1，解得 b=2 ∴二次函数的表达式为 y=-（x-2）2＋9 ∴当 y=0 时，得 x1=5，x2=-1， ∴A（5，0）． 观察图象可得，当 mx＋5＞-（x-b）2＋4b＋1 时， x 的取值范围为 x＜0 或 x＞5． （3）如图 2，∵直线 y=4x＋1 与直线 AB 交于点 E，与 y 轴交于点 F，而直线 AB 表达式为 y=-x＋5， 解方程组 ，得 ∴点 E（ ， ），F（0，1） ∵点 M 在△AOB 内， ∴0y2 ， 当 y1=y2 ， 当 y1