九年级数学上册第二十四章 三角形的内切圆圆24-2点和圆直线和圆的位置关系24-2 16页

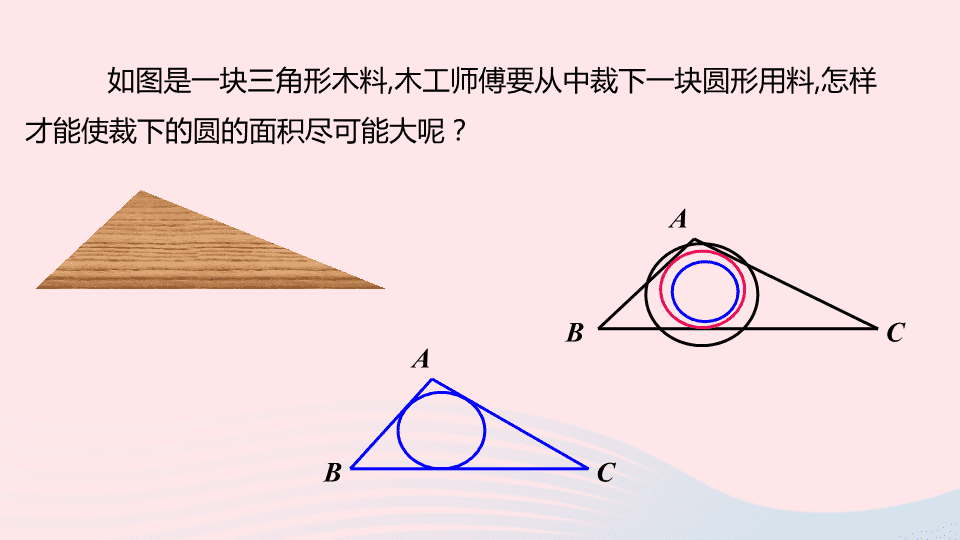
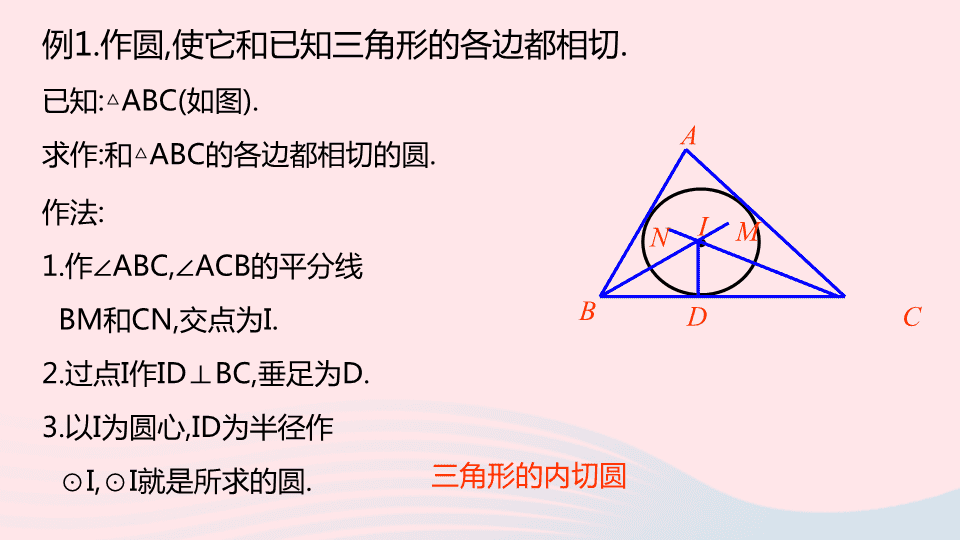
第 24 章 三角形的内切圆 24.2.2 直线与圆（ 3 ） 如图是一块三角形木料 , 木工师傅要从中裁下一块圆形用料 , 怎样才能使裁下的圆的面积尽可能大呢？ A B C A B C 例 1. 作圆 , 使它和已知三角形的各边都相切 . 已知 :△ABC( 如图 ). 求作 : 和△ ABC 的各边都相切的圆 . 作法 : 1. 作∠ ABC,∠ACB 的平分线 BM 和 CN, 交点为 I. 2. 过点 I 作 ID⊥BC, 垂足为 D. 3. 以 I 为圆心 ,ID 为半径作 ⊙ I,⊙I 就是所求的圆 . C B M I A N D 三角形的内切圆 1. 如图 1,△ABC 是⊙ O 的 三角形 .⊙O 是△ ABC 的 圆 , 点 O 叫△ ABC 的 , 它是三角形 的交点 . 外接 内接 外心 三边中垂线 1 2. 定义 : 和三角形各边都相切的圆叫做 ______________, 内切圆的圆心叫做三角形的 __________________ , 这个三角形叫做 . A B C O ． 图 1 三角形的内切圆 内心 圆的外切三角形 3. 如图 2,△DEF 是⊙ I 的 三角形 , ⊙I 是△ DEF 的 圆 , 点 I 是△ DEF 的 ___________ 心 , 它是 的交点 . I D E F ． 图 2 外切 内切 内 角平分线 I 三角形内心的性质： 1. 三角形的内心到三角形各边的距离相等 ; 2. 三角形的内心在三角形的角平分线上 ; 1. 三角形的外心到三角形各个顶点的距离相等 ; 2. 三角形的外心在三角形三边的垂直平分 ; 线上 三角形外心的性质： C A B ． I. D E F ． .O 定义 : 和多边形各边都相切的圆叫做 , 这个多边形叫做 . 多边形的内切圆 圆的外切多边形 内切 外切 如上图 , 四边形 DEFG 是⊙ O 的 四 边形 ,⊙O 是四边形 DEFG 的 圆 . D E F G .O 如图 , 四边形 ABCD 的边 AB,BC,CD,DA 和⊙ O 分别相切于 L,M,N,P. (1) 图中有几对相等的线段 ? A D L M N P O C B (2) 由此你能发现什么结论 ? 为什么 ? ∵ AB,BC,CD,DA 都与⊙ O 相切 , L,M,N,P 是切点 , ∴ AL=AP,LB=MB, DN=DP,NC=MC ∴ AL+ LB+DN+ NC = AP+ MB+DP+MC 即 AB+ CD = AD+BC 圆的外切四边形的两组对边的和相等（可做定理用） 定理：圆的外切四边形的两组对边和相等 . 比较圆的内接四边形的性质： 圆的内接四边形：角的关系 圆的外切四边形：边的关系 练习 : 已知圆外切四边形 ABCD 中 , AB∶BC∶CD= 4∶3∶2, 它的周长为 24cm. 则 AB= ,BC= ; CD= ,DA= . A D O C B 8cm 6cm 4cm 6cm 等腰梯形各边都与⊙ O 相切 , ⊙ O 的直径为 6cm, 等腰梯形的腰等于 8cm, 则梯形的面积为 _______. 8 6 8 48cm 2 判断题： 1. 三角形的内心到三角形各个顶点的距离相等 .( ) 2. 三角形的外心到三角形各边的距离相等 .( ) 3. 等边三角形的内心和外心重合 . ( ) 4. 三角形的内心一定在三角形的内部 . ( ) 5. 菱形一定有内切圆 . ( ) 6. 矩形一定有内切圆 . ( ) 错 错 对 对 错 对 A B C O (2) 若∠ A =80°, 则∠ BOC = _________ 度 . (3) 若∠ BOC =100°, 则∠ A = ________ 度 . 130 20 例 2. 如图 , 在△ ABC 中 , 点 O 是内心 . (1) 若∠ ABC=50°,∠ACB=70°, 求∠ BOC 的度数 . O 是内心 ,∠A 与∠ BOC 之间存在怎样的数量关系 ? 请说明理由 . 理由 :∵ 点 O 是△ ABC 的内心 , 答 :∠BOC=90 °+ 1/2∠A ∴ ∠ OBC= 1/2 ∠ABC, ∠OCB= 1/2 ∠ACB ∴ ∠ OBC ＋∠ OCB = 1/2(∠ABC+∠ACB) = 1/2 （ 180° － ∠ A ） = 90 ° － 1/2 ∠ A ∴ ∠ BOC =180 ° － ( ∠OBC ＋ ∠ OCB ) =180° － ( 90° － 1/2 ∠ A )= 90°+ 1/2 ∠A △ ABC 中 ,AB=50,BC=40,AC=30, 求 三角形内切圆的半径 . O B D E A C F 设 O 是△ ABC 的内心 ,⊙O 的半径为 r 米 , 连接 AO 、 BO 、 CO,⊙O 分别切 AC 、 BC 、 AB 于点 D 、 E 、 F,MD⊥AC,OE⊥BC,OF⊥AB, 则 OD= OE= OF=r, ∵AC=30,BC=40,AB=50 ∴AD=AF=30-r, BE=BF=40-r ∵AB=AF+BF ∴(30+r)+(40-r)=50 ∴ 解 : 已知 : 如图 , ⊙O 是 Rt△ABC 的内切圆 ,∠C 是直角 , 三边长分别是 a,b,c. 求 ⊙ O 的半径 r . A B C ● ┗ ┏ ┓ O D E F ┗ 直角三角形的三边长与其内切圆半径间的关系 . 1. 三角形内切圆的作法 ; 2. 类比三角形的外接圆与圆的内接三角形概念与三角形的内切圆 , 圆的外切三角形概念 . 要明确“接”和“切”的含义 , 弄清“内心”与“外心”的区别 ; 3. 直角三角形内切圆半径的公式 , 以及圆的外切四边形的性质 . 谈谈你的收获