2010中考数学济宁考试试题 13页

‎☆绝密级　　 试卷类型A 济宁市二○一○年高中阶段学校招生考试 数 学 试 题 注意事项：‎ ‎1.本试题分第Ⅰ卷和第Ⅱ卷两部分，共10页.第Ⅰ卷2页为选择题，30分；第Ⅱ卷8页为非选择题，70分；共100分.考试时间为120分钟.‎ ‎2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上. 每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑，如需改动，必须先用橡皮擦干净，再改涂其他答案.‎ ‎3.答第Ⅱ卷时，将密封线内的项目填写清楚，并将座号填写在第8页右侧，用钢笔或圆珠笔直接答在试卷上.考试结束，试题和答题卡一并收回.‎ 第Ｉ卷(选择题　共30分)‎ 一、选择题（下列各题的四个选项中，只有一顶符合题意，每小题3分，共30分）‎ ‎1. 4的算术平方根是 A. 2 B. －‎2 C. ±2 D. 4‎ ‎2. 据统计部门报告，我市去年国民生产总值为238 770 000 000元， 那么这个数据用科学记数法表示为 A. 2. 3877×10 12元 B. 2. 3877×10 11元 C. 2 3877×10 7元 D. 2387. 7×10 8元 ‎3．若一个三角形三个内角度数的比为2︰3︰4，那么这个三角形是 A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 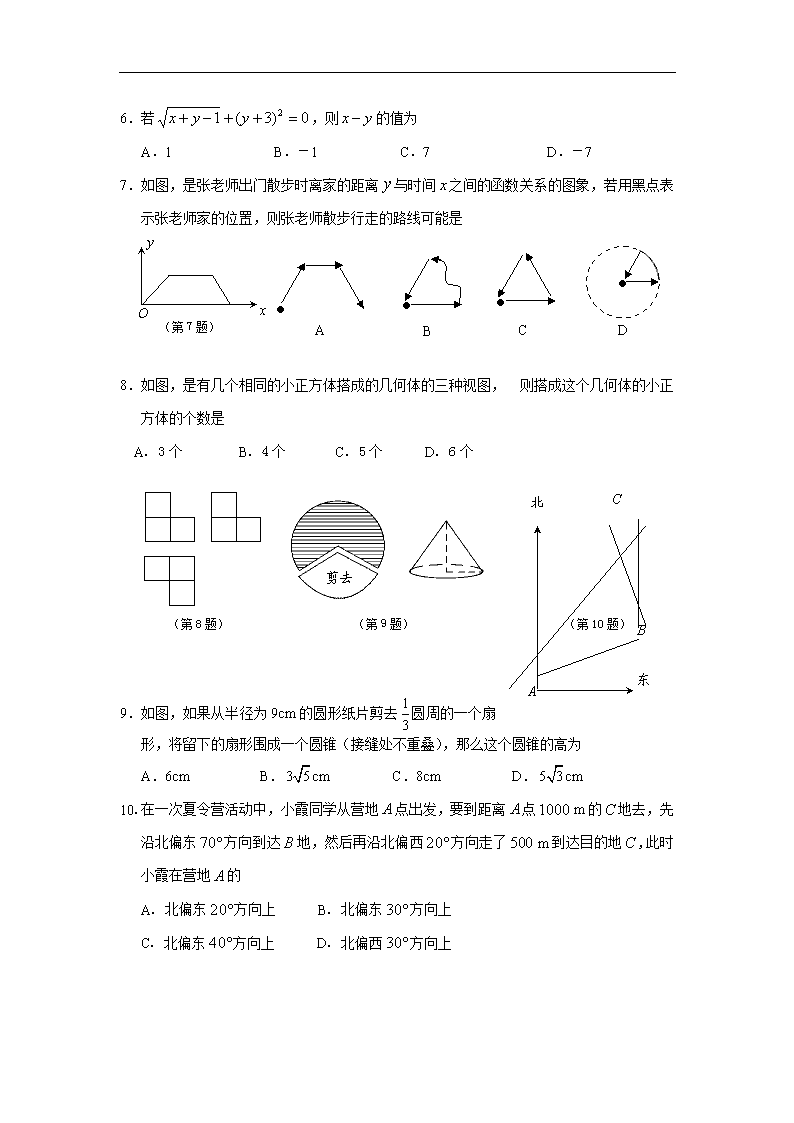等边三角形 ‎ ‎4．把代数式 分解因式，结果正确的是 A． B． ‎ C． D．‎ ‎5．已知⊙O1与⊙O2相切，⊙O1的半径为‎3 cm，⊙O2的半径为‎2 cm，则O1O2的长是 A．‎1 cm B．‎5 cm C．‎1 cm或‎5 cm D．‎0.5cm或‎2.5cm ‎6．若，则的值为 ‎ A．1 B．－‎1 ‎C．7 D．－7‎ ‎7．如图，是张老师出门散步时离家的距离与时间之间的函数关系的图象，若用黑点表示张老师家的位置，则张老师散步行走的路线可能是 ‎（第7题）‎ A B C D ‎8．如图，是有几个相同的小正方体搭成的几何体的三种视图， 则搭成这个几何体的小正方体的个数是 ‎ A. 3个 B. 4个 C. 5个 D. 6个 北 东 ‎（第10题）‎ ‎（第8题）‎ ‎（第9题）‎ 剪去 ‎9．如图，如果从半径为‎9cm的圆形纸片剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为 A．‎6cm B．cm C．‎8cm D．cm ‎10. 在一次夏令营活动中，小霞同学从营地点出发，要到距离点的地去，先沿北偏东方向到达地，然后再沿北偏西方向走了到达目的地,此时小霞在营地的 A. 北偏东方向上 B. 北偏东方向上 ‎ C. 北偏东方向上 D. 北偏西方向上 ‎☆绝密级　　 试卷类型A 济宁市二○一○年高中阶段学校招生考试 数 学 试 题 第Ⅱ卷(非选择题　共70分)‎ 得分 评卷人 ‎ ‎ 二、填空题(每小题3分，共15分；只要求填写最后结果)‎ ‎11．在函数中, 自变量的取值范围是 .‎ ‎12．若代数式可化为，则的值是 ．‎ ‎(第13题)‎ ‎13. 如图，是经过某种变换后得到的图形.如果中任意一点的坐标为（，），那么它的对应点的坐标为 .‎ ‎·‎ ‎·‎ ‎(第15题)‎ ‎14．某校举行以“保护环境，从我做起”为主题的演讲比赛．经预赛，七、八年级各有一名同学进入决赛，九年级有两名同学进入决赛．前两名都是九年级同学的概率是 .‎ ‎15．如图，是一张宽的矩形台球桌，一球从点（点在长边上）出发沿虚线射向边，然后反弹到边上的点. 如果，.那么点与点的距离为 .‎ 三、解答题（共55分，解答应写出文字说明、证明过程或推演步骤）‎ 得分 评卷人 ‎ ‎ ‎16．（5分）‎ 计算：‎ 得分 评卷人 ‎ ‎ ‎17．（5分）‎ 上海世博会自‎2010年5月1日到‎10月31日，历时184天.预测参观人数达7000万人次.如图是此次盛会在5月中旬入园人数的统计情况.‎ ‎（1）请根据统计图完成下表．‎ 众数 中位数 极差 入园人数/万 ‎（2）推算世博会期间参观总人数与预测人数相差多少？‎ 得分 评卷人 ‎ ‎ ‎18．（6分）‎ 观察下面的变形规律：‎ ‎ ＝1－； ＝－；＝－；……‎ 解答下面的问题：‎ ‎（1）若n为正整数，请你猜想＝ ；‎ ‎（2）证明你猜想的结论；‎ ‎（3）求和：＋＋＋…＋ .‎ 得分 评卷人 ‎ ‎ ‎19．（6分）‎ 如图，为外接圆的直径，，垂足为点，的平分线交于点，连接，.‎ ‎(1) 求证：； ‎ ‎(第19题)‎ ‎(2) 请判断，，三点是否在以为圆心，以为半径的圆上？并说明理由.‎ 得分 评卷人 ‎ ‎ ‎20．（7分）‎ 如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为1.‎ ‎（1）求反比例函数的解析式；‎ ‎(第20题)‎ ‎（2）如果为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小.‎ 得分 评卷人 ‎ ‎ ‎21．（8分）‎ 某市在道路改造过程中，需要铺设一条长为‎1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设‎20米，且甲工程队铺设‎350米所用的天数与乙工程队铺设‎250米所用的天数相同.‎ ‎（1）甲、乙工程队每天各能铺设多少米？‎ ‎（2）如果要求完成该项工程的工期不超过10天，那么为两工程队分配工程量（以百米为单位）的方案有几种？请你帮助设计出来.‎ 得分 评卷人 ‎ ‎ ‎22．（8分）‎ ‎(第22题)‎ 数学课上，李老师出示了这样一道题目：如图，正方形的边长为，为边延长线上的一点，为的中点，的垂直平分线交边于，交边的延长线于.当时，与的比值是多少？‎ 经过思考，小明展示了一种正确的解题思路：过作直线平行于交，分别于，，如图，则可得：，因为，所以.可求出和的值，进而可求得与的比值.‎ ‎(1) 请按照小明的思路写出求解过程.‎ ‎(2) 小东又对此题作了进一步探究，得出了 的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.‎ 得分 评卷人 ‎ ‎ ‎23．（10分）‎ 如图，在平面直角坐标系中，顶点为（，）的抛物线交轴于点，交轴于，两点（点在点的左侧）. 已知点坐标为（，）.‎ ‎（1）求此抛物线的解析式；‎ ‎（2）过点作线段的垂线交抛物线于点， 如果以点为圆心的圆与直线相切，请判断抛物线的对称轴与⊙有怎样的位置关系，并给出证明；‎ ‎(第23题)‎ ‎（3）已知点是抛物线上的一个动点，且位于，两点之间，问：当点运动到什么位置时，的面积最大？并求出此时点的坐标和的最大面积.‎ ‎☆绝密级 试卷类型A 济宁市二○一○年高中阶段学校招生考试 数学试题参考答案及评分标准 说明：‎ 解答题各小题只给出了一种解法及评分标准．其他解法，只要步骤合理，解答正确，均应给出相应的分数．‎ 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A B B D C C D B B C 二、填空题 ‎11．； 12．5； 13．（，）； 14．； 15．．‎ 三、解答题 ‎16．解：原式 4分 ‎ 5分 ‎17．（1）24，24，16 3分 ‎（2）解：‎ ‎(万)‎ 答：世博会期间参观总人数与预测人数相差2418.4万 5分 ‎18．（1） 1分 ‎（2）证明：－＝－＝＝. 3分 ‎（3）原式＝1－＋－＋－＋…＋－‎ ‎ ＝. 5分 ‎19．（1）证明：∵为直径，，‎ ‎∴.∴. 3分 ‎（2）答：，，三点在以为圆心，以为半径的圆上. 4分 理由：由（1）知：，∴.‎ ‎∵，，，‎ ‎∴.∴. 6分 由（1）知：.∴.‎ ‎∴，，三点在以为圆心，以为半径的圆上. 7分 ‎20．解：（1） 设点的坐标为（，），则.∴.‎ ‎∵,∴.∴.‎ ‎∴反比例函数的解析式为. 3分 ‎(2) 由 得 ∴为（，）. 4分 设点关于轴的对称点为，则点的坐标为（，）.‎ 令直线的解析式为.‎ ‎∵为（，）∴∴‎ ‎∴的解析式为. 6分 当时，.∴点为（，）. 7分 ‎21.（1）解：设甲工程队每天能铺设米，则乙工程队每天能铺设（）米.‎ 根据题意得：. 2分 解得.‎ 检验: 是原分式方程的解.‎ 答：甲、乙工程队每天分别能铺设米和米. 4分 ‎（2）解：设分配给甲工程队米，则分配给乙工程队（）米.‎ 由题意，得解得． 6分 所以分配方案有3种．‎ 方案一：分配给甲工程队米，分配给乙工程队米；‎ 方案二：分配给甲工程队米，分配给乙工程队米；‎ 方案三：分配给甲工程队米，分配给乙工程队米． 8分 ‎22．（1）解：过作直线平行于交，分别于点，， ‎ 则，，.‎ ‎∵，∴. 2分 ‎∴，.‎ ‎∴. 4分 ‎（2）证明：作∥交于点， 5分 则，.‎ ‎∵，‎ ‎∴.‎ ‎∵，，‎ ‎∴.∴. 7分 ‎(第23题)‎ ‎∴. 8分 ‎(第22题)‎ ‎23．（1）解：设抛物线为.‎ ‎∵抛物线经过点（0，3），∴.∴.‎ ‎∴抛物线为. ……………………………3分 ‎ (2) 答：与⊙相交. …………………………………………………………………4分 证明：当时，，.‎ ‎ ∴为（2，0），为（6，0）.∴.‎ 设⊙与相切于点，连接，则.‎ ‎∵，∴.‎ 又∵，∴.∴∽.‎ ‎∴.∴.∴.…………………………6分 ‎∵抛物线的对称轴为，∴点到的距离为2.‎ ‎∴抛物线的对称轴与⊙相交. ……………………………………………7分 ‎(3) 解：如图，过点作平行于轴的直线交于点.‎ 可求出的解析式为.…………………………………………8分 设点的坐标为（，），则点的坐标为（，）.‎ ‎ ∴.‎ ‎ ∵,‎ ‎ ∴当时，的面积最大为.‎ ‎ 此时，点的坐标为（3，）. …………………………………………10分 ‎ ‎