中考九年级数学学练测93弧长及扇形的面积 48页

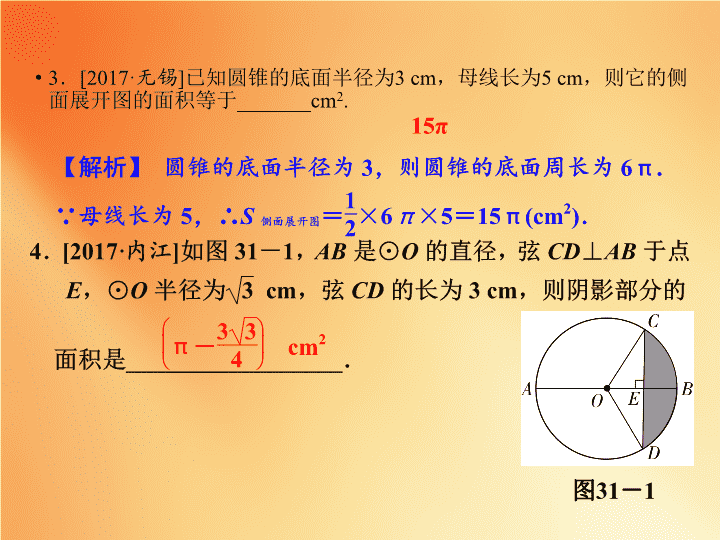
弧长及扇形的面积、圆锥的侧面积和全面积 1 ． [2017· 泰州 ] 扇形的半径为 3 cm ，弧长为 2 π cm ，则该扇形的面积为 _______cm 2 . 2 ． [2017· 温州 ] 已知扇形的面积为 3 π ，圆心角为 120° ，则它的半径为 ______ ． 小题热身 3 π 3 3 ． [2017· 无锡 ] 已知圆锥的底面半径为 3 cm ，母线长为 5 cm ，则它的侧面展开图的面积等于 _______cm 2 . 图 31 － 1 15 π 5 ． [2016· 盐城 ] 如图 31 － 2 ，正六边形 ABCDEF 内接于半径为 4 的圆，则 B ， E 两点间的距离为 _____ ． 图 31 － 2 8 一、必知 4 知识点 1 ．正多边形和圆 正多边形：各边相等，各内角也相等的多边形叫做正多边形． 正多边形的外接圆：经过一个正多边形的各个顶点的圆叫做这个正多边形的 __________ ． 圆内接正多边形：这个正多边形叫做圆内接正多边形． 正多边形的对称性：正多边形是轴对称图形． 考点管理 外接圆 【 智慧锦囊 】 正多边形的有关计算： 2 ．圆的周长与弧长公式 圆的周长：若圆的半径是 R ，则圆的周长 C ＝ ______ ． 弧长公式：若一条弧所对的圆心角是 n ° ，半径是 R ，则弧 长 l ＝ __________ ． 3 ．扇形的面积公式 (1) 对于半径是 R ，圆心角是 n ° 的扇形的面积是 S ＝ ________ ①； (2) 对于弧长是 l ，半径是 R 的扇形的面积是 S ＝ ________②. 说明：当已知半径 R 和圆心角的度数求扇形的面积时，选用公式 ① ；当已知半径 R 和弧长求扇形的面积时，应选用公式 ②. π R 4 ．圆锥的侧面积和全面积 圆锥侧面展开图：沿着圆锥的母线，把圆锥的侧面展开，得到一个扇形，这个扇形的弧长等于圆锥底面的周长，而扇形的半径等于圆锥的 ________ 长． 圆锥侧面积与全面积：如图 31 － 3 ，若圆锥 的底面半径为 r ，母线长为 l ，则它的侧面 积 S 侧 ＝ _______ ；全面积 S 全 ＝ __________ ． 图 31 － 3 【 智慧锦囊 】 圆锥的基本特征： (1) 圆锥的母线长都相等； (2) 圆锥的侧面展开图是半径等于母线长，弧长等于圆锥底面周长的扇形． 母线 π rl π r 2 ＋ π rl 二、必会 2 方法 1 ．三招教你求阴影部分的面积 思路： (1) 将所求阴影部分的面积转化为已学过的易求图形的面积和差； (2) 适当作辅助线，将所求阴影部分面积割补为学过易求图形的面积． 方法： (1) 作差法； (2) 割补法； (3) 等积变形法． 2 ．解圆锥 ( 柱 ) 题的 “ 四字诀 ”—— 展，围，转，剖 展：把一个圆锥 ( 柱 ) 的侧面沿着它的一条母线剪开后展在一个平面上； 围：将扇形围成圆锥侧面或矩形卷成圆柱的侧面； 转：圆锥 ( 柱 ) 可以看成是由一个直角三角形 ( 矩形 ) 旋转得到的； 剖：对圆锥 ( 柱 ) 沿着它的轴将其一分为二，所得到的截面一般是等腰三角形 ( 矩形 ) ，这个等腰三角形的腰长等于圆锥的母线长，底边长等于圆锥的底面直径 ( 矩形的一边长等于圆柱的母线长，另一边长等于圆柱的底面直径 ) ． 正多边形的性质 [2017· 达州 ] 以半径为 2 的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是 ( 　 　 ) A 例 1 答图 1 ． [2017· 滨州 ] 若正方形的外接圆半径为 2 ，则其内切圆半径为 ( 　 　 ) 变式跟进 1 答图 A A ． 3 B ． 4 C ． 5 D ． 6 C 图 31 － 4 变式跟进 2 答图 3 ． [2016· 威海 ] 如图 31 － 5 ，正方形 ABCD 内接于 ⊙ O ，其边长 为 4 ，则 ⊙ O 的内接正三角形 △ EFG 的边长为 ________ ． 图 31 － 5 变式跟进 3 答图 弧长计算 图 31 － 6 20 π 1 ． [2016· 兰州 ] 如图 31 － 7 ，用一个半径为 5 cm 的定滑轮带动重物上升，滑轮上一点 P 旋转了 108° ，假设绳索 ( 粗细不计 ) 与滑轮之间没有滑动，则重物上升了 ( 　 　 ) A ． π cm B ． 2π cm C ． 3π cm D ． 5π cm 图 31 － 7 C 2 ． [2017· 菏泽 ] 一个扇形的圆心角为 100° ，面积为 15π cm 2 ， 则此扇形的半径长为 _______cm. 3 ．已知扇形的圆心角为 120° ，弧长为 2π ，则它的半径为 _____ ． 3 扇形的面积计算 　 [2017· 丽水 ] 如图 31 － 8 ，点 C 是以 AB 为直径的半圆 O 的三等分点， AC ＝ 2 ，则图中阴影部分的面积是 ( 　 　 ) 图 31 － 8 A 例 3 答图 图 31 － 9 (48 π ＋ 32)cm 2 变 式跟进 1 答图 2 ． [2016· 宁波 ] 如图 31 － 10 ，半圆 O 的直径 AB ＝ 2 ，弦 CD ∥ AB ，∠ COD ＝ 90° ，则图中阴影部分的面积为 ____ ． 图 31 － 10 3 ．如图 31 － 11 ，在 △ ABC 中， AB ＝ AC ，以 AB 为直径的 ⊙ O 分别与 BC ， AC 交于点 D ， E ，过点 D 作 ⊙ O 的切线 DF ，交 AC 于点 F . (1) 求证： DF ⊥ AC ； (2) 若 ⊙ O 的半径为 4 ，∠ CDF ＝ 22.5° ，求阴影部分的面积． 图 31 － 11 解 ： (1) 证明：如答图，连结 OD . ∵ OB ＝ OD ，∴∠ ABC ＝ ∠ ODB . ∵ AB ＝ AC ，∴∠ ABC ＝ ∠ ACB . ∴∠ ODB ＝ ∠ ACB .∴ OD ∥ AC . ∵ DF 是 ⊙ O 的切线， ∴ DF ⊥ OD ，∴ DF ⊥ AC ； (2) 如答图，连结 OE . ∵ DF ⊥ AC ，∠ CDF ＝ 22.5° ， ∴∠ ABC ＝ ∠ ACB ＝ 67.5° ， ∴∠ BAC ＝ 45°. ∵ OA ＝ OE ，∴∠ AOE ＝ 90°. 变式跟进 3 答图 ∵⊙ O 的半径为 4 ，∴ S 扇形 AOE ＝ 4π ， S △ AOE ＝ 8. ∴ S 阴影 ＝ S 扇形 AOE － S △ AOE ＝ 4π － 8. 【 点悟 】 　求不规则图形的面积，常转化为易解决问题的基本图形，然后求出各图形的面积，通过面积的和差求出结果． 圆锥 ( 柱 ) 侧面展开图和全面积的计算 [2017· 杭州 ] 如图 31 － 12 ，在 Rt △ ABC 中， ∠ ABC ＝ 90° ， AB ＝ 2 ， BC ＝ 1. 把 △ ABC 分 别绕直线 AB 和 BC 旋转一周，所得几何体的 底面圆的周长分别记做 l 1 ， l 2 ，侧面积分别 记做 S 1 ， S 2 ，则 ( 　 　 ) A ． l 1 ∶ l 2 ＝ 1∶2 ， S 1 ∶ S 2 ＝ 1∶2 B ． l 1 ∶ l 2 ＝ 1∶4 ， S 1 ∶ S 2 ＝ 1∶2 C ． l 1 ∶ l 2 ＝ 1∶2 ， S 1 ∶ S 2 ＝ 1∶4 D ． l 1 ∶ l 2 ＝ 1∶4 ， S 1 ∶ S 2 ＝ 1∶4 图 31 － 12 A 1 ． [2017· 南充 ] 如图 31 － 13 ，在 Rt △ ABC 中， AC ＝ 5 cm ， BC ＝ 12 cm ，∠ ACB ＝ 90° ，把 Rt △ ABC 绕 BC 所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为 ( 　 　 ) A ． 60π cm 2 B ． 65π cm 2 C ． 120π cm 2 D ． 130π cm 2 图 31 － 13 B 2 ． [2016· 宁波 ] 如图 31 － 14 ，圆锥的底面半径 r 为 6 cm ，高 h 为 8 cm ，则圆锥的侧面积为 ( 　 　 ) A ． 30π cm 2 B ． 48π cm 2 C ． 60π cm 2 D ． 80π cm 2 图 31 － 14 C 3 ． [2017· 绵阳 ]“ 赶陀螺 ” 是一项深受人们喜爱的运动．如图 31 － 15 所示是一个陀螺的立体结构图．已知底面圆的直径 AB ＝ 8 cm ，圆柱体部分的高 BC ＝ 6 cm ，圆锥体部分的高 CD ＝ 3 cm ，则这个陀螺的表面积是 ( 　 　 ) A ． 68π cm 2 B ． 74π cm 2 C ． 84π cm 2 D ． 100π cm 2 图 31 － 15 C 【 解析 】 圆锥的表面积加上圆柱的侧面积及底面圆的面积即可求得其表面积． ∵ 底面圆的直径为 8 cm ，锥高为 3 cm ，∴圆锥的母线长为 5 cm ，∴表面积＝ π×4×5 ＋ 8π×6 ＋ 16π ＝ 84π(cm 2 ) ，故选 C. 平面图形的滚动问题 　 [2017· 达州 ] 如图 31 － 16 ，将矩形 ABCD 绕其右下角的顶点按顺时针方向旋转至 ① 位置，继续绕右下角的顶点按顺时针方向旋转至 ② 位置，以此类推，这样连续旋转 2 017 次．若 AB ＝ 4 ， AD ＝ 3 ，则顶点 A 在整个旋转过程中所经过的路径总长为 ( 　 　 ) A ． 2 017π B ． 2 034π C ． 3 024π D ． 3 026π 图 31 － 16 D 图 31 － 17 A 2 ． [2016· 烟台 ] 如图 31 － 18 ， C 为半圆内一点， O 为圆心，直径 AB 长为 2 cm ， ∠ BOC ＝ 60° ，∠ BCO ＝ 90° ，将 △ BOC 绕圆心 O 逆时针旋转至△ B ′ OC ′ ，点 C ′ 在 OA 上，则边 BC 扫过区域 ( 图中阴影 部分 ) 的面积为 ______cm 2 . 图 31 － 18 图 31 － 19 4 ．如图 31 － 20 ，半径为 5 的半圆的初始状态是直径平行于桌面上的直线 b ，然后把半圆沿直线 b 进行无滑动滚动，使半圆的直径与直线 b 重合为止，则圆心 O 运动路径的长度等于 ______ ． 图 31 － 20 5 π 变式跟进 4 答图 必明 2 易错点 2 ． (1) 圆锥有无数条母线，圆锥的母线长不等于圆锥的高； (2) 圆锥的母线长为侧面展开后所得扇形的半径，注意与圆锥底面半径区分开． “圆锥底面圆半径 ” 不同于 “ 展开图扇形的半径 ” 已知圆锥的侧面展开图的圆心角是 180° ，底面积为 15 cm 2 ， 则圆锥的侧面积为 ________ ． 【 错因 】 把圆锥底面圆的半径当成展开图的扇形半径，混淆了 对应关系． 【 点悟 】 　圆锥的侧面积等于展开后扇形的面积，扇形的半径 为圆锥的母线长，弧长为圆锥的底面圆的周长．