2019年山东省潍坊市中考数学试卷含答案 29页

‎2019年山东省潍坊市中考数学试卷 一、选择题（本大题共12小题，共36分。在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得3分，错选、不选或选出的答案超过一个均记0分）‎ ‎1．（3分）2019的倒数的相反数是（　　）‎ A．﹣2019 B．‎-‎‎1‎‎2019‎ C．‎1‎‎2019‎ D．2019‎ ‎2．（3分）下列运算正确的是（　　）‎ A．3a×2a＝6a B．a8÷a4＝a2 ‎ C．﹣3（a﹣1）＝3﹣3a D．（‎1‎‎3‎a3）2‎=‎‎1‎‎9‎a9‎ ‎3．（3分）“十三五”以来，我国启动实施了农村饮水安全巩固提升工程．截止去年9月底，各地已累计完成投资1.002×1011元．数据1.002×1011可以表示为（　　）‎ A．10.02亿 B．100.2亿 C．1002亿 D．10020亿 ‎4．（3分）如图是由10个同样大小的小正方体摆成的几何体．将小正方体①移走后，则关于新几何体的三视图描述正确的是（　　）‎ A．俯视图不变，左视图不变 ‎ B．主视图改变，左视图改变 ‎ C．俯视图不变，主视图不变 ‎ D．主视图改变，俯视图改变 ‎5．（3分）利用教材中时计算器依次按键下：‎ 则计算器显示的结果与下列各数中最接近的一个是（　　）‎ A．2.5 B．2.6 C．2.8 D．2.9‎ ‎6．（3分）下列因式分解正确的是（　　）‎ A．3ax2﹣6ax＝3（ax2﹣2ax） B．x2+y2＝（﹣x+y）（﹣x﹣y） ‎ C．a2+2ab﹣4b2＝（a+2b）2 D．﹣ax2+2ax﹣a＝﹣a（x﹣1）2‎ ‎7．（3分）小莹同学10个周综合素质评价成绩统计如下：‎ 成绩（分）‎ ‎94‎ ‎95‎ ‎97‎ ‎98‎ ‎100‎ 周数（个）‎ ‎1‎ ‎2‎ ‎2‎ ‎4‎ ‎1‎ 这10个周的综合素质评价成绩的中位数和方差分别是（　　）‎ A．97.5 2.8 B．97.5 3 ‎ C．97 2.8 D．97 3‎ ‎8．（3分）如图，已知∠AOB．按照以下步骤作图：‎ ‎①以点O为圆心，以适当的长为半径作弧，分别交∠AOB的两边于C，D两点，连接CD．‎ ‎②分别以点C，D为圆心，以大于线段OC的长为半径作弧，两弧在∠AOB内交于点E，连接CE，DE．‎ ‎③连接OE交CD于点M．‎ 下列结论中错误的是（　　）‎ A．∠CEO＝∠DEO B．CM＝MD ‎ C．∠OCD＝∠ECD D．S四边形OCED‎=‎‎1‎‎2‎CD•OE ‎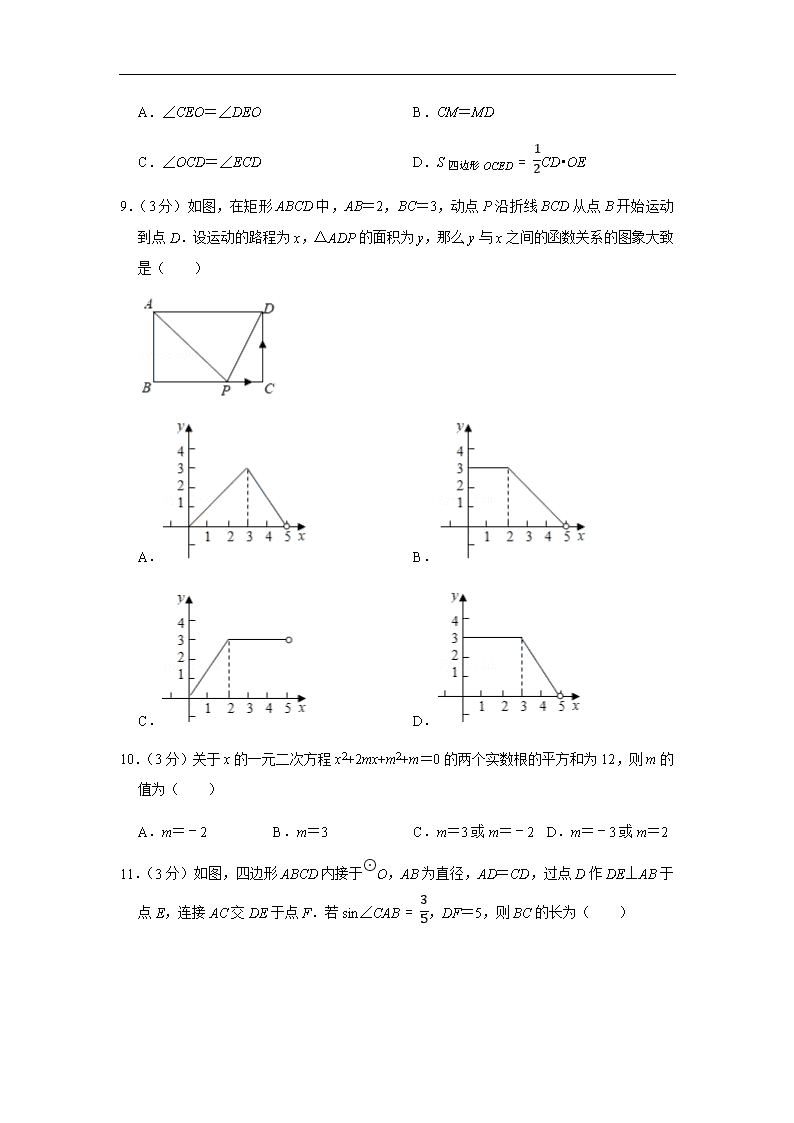9．（3分）如图，在矩形ABCD中，AB＝2，BC＝3，动点P沿折线BCD从点B开始运动到点D．设运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是（　　）‎ A． B． ‎ C． D．‎ ‎10．（3分）关于x的一元二次方程x2+2mx+m2+m＝0的两个实数根的平方和为12，则m的值为（　　）‎ A．m＝﹣2 B．m＝3 C．m＝3或m＝﹣2 D．m＝﹣3或m＝2‎ ‎11．（3分）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过点D作DE⊥AB于点E，连接AC交DE于点F．若sin∠CAB‎=‎‎3‎‎5‎，DF＝5，则BC的长为（　　）‎ A．8 B．10 C．12 D．16‎ ‎12．（3分）抛物线y＝x2+bx+3的对称轴为直线x＝1．若关于x的一元二次方程x2+bx+3﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数根，则t的取值范围是（　　）‎ A．2≤t＜11 B．t≥2 C．6＜t＜11 D．2≤t＜6‎ 二、填空题（本题共6小题，满分18分。只要求填写最后结果，每小题填对得3分。）‎ ‎13．（3分）若2x＝3，2y＝5，则2x+y＝　 　．‎ ‎14．（3分）当直线y＝（2﹣2k）x+k﹣3经过第二、三、四象限时，则k的取值范围是　 　．‎ ‎15．（3分）如图，Rt△AOB中，∠AOB＝90°，顶点A，B分别在反比例函数y‎=‎‎1‎x（x＞0）与y‎=‎‎-5‎x（x＜0）的图象上，则tan∠BAO的值为　 　．‎ ‎16．（3分）如图，在矩形ABCD中，AD＝2．将∠A向内翻折，点A落在BC上，记为A′，折痕为DE．若将∠B沿EA′向内翻折，点B恰好落在DE上，记为B′，则AB＝　 　．‎ ‎17．（3分）如图，直线y＝x+1与抛物线y＝x2﹣4x+5交于A，B两点，点P是y轴上的一个动点，当△PAB的周长最小时，S△PAB＝　 　．‎ ‎18．（3分）如图所示，在平面直角坐标系xoy中，一组同心圆的圆心为坐标原点O，它们的半径分别为1，2，3，…，按照“加1”依次递增；一组平行线，l0，l1，l2，l3，…都与x轴垂直，相邻两直线的间距为l，其中l0与y轴重合若半径为2的圆与l1在第一象限内交于点P1，半径为3的圆与l2在第一象限内交于点P2，…，半径为n+1的圆与ln在第一象限内交于点Pn，则点Pn的坐标为　 　．（n为正整数）‎ 三、解答题（本题共7小题，共66分。解答应写出文字说明、证明过程或推演步骤。）‎ ‎19．（5分）己知关于x，y的二元一次方程组‎2x-3y=5‎x-2y=k的解满足x＞y，求k的取值范围．‎ ‎20．（6分）自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多，为方便群众步行健身，某地政府决定对一段如图1所示的坡路进行改造．如图2所示，改造前的斜坡AB＝200米，坡度为1：‎3‎；将斜坡AB的高度AE降低AC＝20米后，斜坡AB改造为斜坡CD，其坡度为1：4．求斜坡CD的长．（结果保留根号）‎ ‎21．（9分）如图所示，有一个可以自由转动的转盘，其盘面分为4等份，在每一等份分别标有对应的数字2，3，4，5．小明打算自由转动转盘10次，现已经转动了8次，每一次停止后，小明将指针所指数字记录如下：‎ 次数 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次 数字 ‎3‎ ‎5‎ ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎3‎ ‎5‎ ‎（1）求前8次的指针所指数字的平均数．‎ ‎（2）小明继续自由转动转盘2次，判断是否可能发生“这10次的指针所指数字的平均数不小于3.3，且不大于3.5”的结果？若有可能，计算发生此结果的概率，并写出计算过程；若不可能，说明理由．（指针指向盘面等分线时为无效转次．）‎ ‎22．（10分）如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M．‎ ‎（1）求证：△AHF为等腰直角三角形．‎ ‎（2）若AB＝3，EC＝5，求EM的长．‎ ‎23．（10分）扶贫工作小组对果农进行精准扶贫，帮助果农将一种有机生态水果拓宽了市场．与去年相比，今年这种水果的产量增加了1000千克，每千克的平均批发价比去年降低了1元，批发销售总额比去年增加了20%．‎ ‎（1）已知去年这种水果批发销售总额为10万元，求这种水果今年每千克的平均批发价是多少元？‎ ‎（2）某水果店从果农处直接批发，专营这种水果．调查发现，若每千克的平均销售价为41元，则每天可售出300千克；若每千克的平均销售价每降低3元，每天可多卖出180千克，设水果店一天的利润为w元，当每千克的平均销售价为多少元时，该水果店一天的利润最大，最大利润是多少？（利润计算时，其它费用忽略不计．）‎ ‎24．（13分）如图1，菱形ABCD的顶点A，D在直线上，∠BAD＝60°，以点A为旋转中心将菱形ABCD顺时针旋转α（0°＜α＜30°），得到菱形AB′C′D′，B′C′交对角线AC于点M，C′D′交直线l于点N，连接MN．‎ ‎（1）当MN∥B′D′时，求α的大小．‎ ‎（2）如图2，对角线B′D′交AC于点H，交直线l与点G，延长C′B′交AB于点E，连接EH．当△HEB′的周长为2时，求菱形ABCD的周长．‎ ‎25．（13分）如图，在平面直角坐标系xoy中，O为坐标原点，点A（4，0），点B（0，4），△ABO的中线AC与y轴交于点C，且⊙M经过O，A，C三点．‎ ‎（1）求圆心M的坐标；‎ ‎（2）若直线AD与⊙M相切于点A，交y轴于点D，求直线AD的函数表达式；‎ ‎（3）在过点B且以圆心M为顶点的抛物线上有一动点P，过点P作PE∥y轴，交直线AD于点E．若以PE为半径的⊙P与直线AD相交于另一点F．当EF＝4‎5‎时，求点P的坐标．‎ ‎2019年山东省潍坊市中考数学试卷 参考答案与试题解析 一、选择题（本大题共12小题，共36分。在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得3分，错选、不选或选出的答案超过一个均记0分）‎ ‎1．（3分）2019的倒数的相反数是（　　）‎ A．﹣2019 B．‎-‎‎1‎‎2019‎ C．‎1‎‎2019‎ D．2019‎ ‎【解答】解：2019的倒数是‎1‎‎2019‎，再求‎1‎‎2019‎的相反数为‎-‎‎1‎‎2019‎；‎ 故选：B．‎ ‎2．（3分）下列运算正确的是（　　）‎ A．3a×2a＝6a B．a8÷a4＝a2 ‎ C．﹣3（a﹣1）＝3﹣3a D．（‎1‎‎3‎a3）2‎=‎‎1‎‎9‎a9‎ ‎【解答】解：A、3a×2a＝6a2，故本选项错误；‎ B、a8÷a4＝a4，故本选项错误；‎ C、﹣3（a﹣1）＝3﹣3a，正确；‎ D、（‎1‎‎3‎a3）2‎=‎‎1‎‎9‎a6，故本选项错误．‎ 故选：C．‎ ‎3．（3分）“十三五”以来，我国启动实施了农村饮水安全巩固提升工程．截止去年9月底，各地已累计完成投资1.002×1011元．数据1.002×1011可以表示为（　　）‎ A．10.02亿 B．100.2亿 C．1002亿 D．10020亿 ‎【解答】解：‎ ‎1.002×1011＝1 002 000 000 00＝1002亿 故选：C．‎ ‎4．（3分）如图是由10个同样大小的小正方体摆成的几何体．将小正方体①移走后，则关于新几何体的三视图描述正确的是（　　）‎ A．俯视图不变，左视图不变 ‎ B．主视图改变，左视图改变 ‎ C．俯视图不变，主视图不变 ‎ D．主视图改变，俯视图改变 ‎【解答】解：将正方体①移走后，‎ 新几何体的三视图与原几何体的三视图相比，俯视图和左视图没有发生改变；‎ 故选：A．‎ ‎5．（3分）利用教材中时计算器依次按键下：‎ 则计算器显示的结果与下列各数中最接近的一个是（　　）‎ A．2.5 B．2.6 C．2.8 D．2.9‎ ‎【解答】解：∵‎7‎‎≈‎2.646，‎ ‎∴与‎7‎最接近的是2.6，‎ 故选：B．‎ ‎6．（3分）下列因式分解正确的是（　　）‎ A．3ax2﹣6ax＝3（ax2﹣2ax） B．x2+y2＝（﹣x+y）（﹣x﹣y） ‎ C．a2+2ab﹣4b2＝（a+2b）2 D．﹣ax2+2ax﹣a＝﹣a（x﹣1）2‎ ‎【解答】解：A、3ax2﹣6ax＝3ax（x﹣2），故此选项错误；‎ B、x2+y2，无法分解因式，故此选项错误；‎ C、a2+2ab﹣4b2，无法分解因式，故此选项错误；‎ D、﹣ax2+2ax﹣a＝﹣a（x﹣1）2，正确．‎ 故选：D．‎ ‎7．（3分）小莹同学10个周综合素质评价成绩统计如下：‎ 成绩（分）‎ ‎94‎ ‎95‎ ‎97‎ ‎98‎ ‎100‎ 周数（个）‎ ‎1‎ ‎2‎ ‎2‎ ‎4‎ ‎1‎ 这10个周的综合素质评价成绩的中位数和方差分别是（　　）‎ A．97.5 2.8 B．97.5 3 ‎ C．97 2.8 D．97 3‎ ‎【解答】解：这10个周的综合素质评价成绩的中位数是‎97+98‎‎2‎‎=‎97.5（分），‎ 平均成绩为‎1‎‎10‎‎×‎（94+95×2+97×2+98×4+100）＝97（分），‎ ‎∴这组数据的方差为‎1‎‎10‎‎×‎[（94﹣97）2+（95﹣97）2×2+（97﹣97）2×2+（98﹣97）2×4+（100﹣97）2]＝3（分2），‎ 故选：B．‎ ‎8．（3分）如图，已知∠AOB．按照以下步骤作图：‎ ‎①以点O为圆心，以适当的长为半径作弧，分别交∠AOB的两边于C，D两点，连接CD．‎ ‎②分别以点C，D为圆心，以大于线段OC的长为半径作弧，两弧在∠AOB内交于点E，连接CE，DE．‎ ‎③连接OE交CD于点M．‎ 下列结论中错误的是（　　）‎ A．∠CEO＝∠DEO B．CM＝MD ‎ C．∠OCD＝∠ECD D．S四边形OCED‎=‎‎1‎‎2‎CD•OE ‎【解答】解：由作图步骤可得：OE是∠AOB的角平分线，‎ ‎∴∠CEO＝∠DEO，CM＝MD，S四边形OCED‎=‎‎1‎‎2‎CD•OE，‎ 但不能得出∠OCD＝∠ECD，‎ 故选：C．‎ ‎9．（3分）如图，在矩形ABCD中，AB＝2，BC＝3，动点P沿折线BCD从点B开始运动到点D．设运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：由题意当0≤x≤3时，y＝3，‎ 当3＜x＜5时，y‎=‎1‎‎2‎×‎3×（5﹣x）‎=-‎‎3‎‎2‎x‎+‎‎15‎‎2‎．‎ 故选：D．‎ ‎10．（3分）关于x的一元二次方程x2+2mx+m2+m＝0的两个实数根的平方和为12，则m的值为（　　）‎ A．m＝﹣2 B．m＝3 C．m＝3或m＝﹣2 D．m＝﹣3或m＝2‎ ‎【解答】解：设x1，x2是x2+2mx+m2+m＝0的两个实数根，‎ ‎∴△＝﹣4m≥0，‎ ‎∴m≤0，‎ ‎∴x1+x2＝﹣2m，x1•x2＝m2+m，‎ ‎∴x12+x22＝（x1+x2）2﹣2x1•x2＝4m2﹣2m2﹣2m＝2m2﹣2m＝12，‎ ‎∴m＝3或m＝﹣2；‎ ‎∴m＝﹣2；‎ 故选：A．‎ ‎11．（3分）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过点D作DE⊥AB于点E，连接AC交DE于点F．若sin∠CAB‎=‎‎3‎‎5‎，DF＝5，则BC的长为（　　）‎ A．8 B．10 C．12 D．16‎ ‎【解答】解：连接BD，如图，‎ ‎∵AB为直径，‎ ‎∴∠ADB＝∠ACB＝90°，‎ ‎∵∠AD＝CD，‎ ‎∴∠DAC＝∠DCA，‎ 而∠DCA＝∠ABD，‎ ‎∴∠DAC＝∠ABD，‎ ‎∵DE⊥AB，‎ ‎∴∠ABD+∠BDE＝90°，‎ 而∠ADE+∠BDE＝90°，‎ ‎∴∠ABD＝∠ADE，‎ ‎∴∠ADE＝∠DAC，‎ ‎∴FD＝FA＝5，‎ 在Rt△AEF中，∵sin∠CAB‎=EFAF=‎‎3‎‎5‎，‎ ‎∴EF＝3，‎ ‎∴AE‎=‎5‎‎2‎‎-‎‎3‎‎2‎=‎4，DE＝5+3＝8，‎ ‎∵∠ADE＝∠DBE，∠AED＝∠BED，‎ ‎∴△ADE∽△DBE，‎ ‎∴DE：BE＝AE：DE，即8：BE＝4：8，‎ ‎∴BE＝16，‎ ‎∴AB＝4+16＝20，‎ 在Rt△ABC中，∵sin∠CAB‎=BCAB=‎‎3‎‎5‎，‎ ‎∴BC＝20‎×‎3‎‎5‎=‎12．‎ 故选：C．‎ ‎12．（3分）抛物线y＝x2+bx+3的对称轴为直线x＝1．若关于x的一元二次方程x2+bx+3﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数根，则t的取值范围是（　　）‎ A．2≤t＜11 B．t≥2 C．6＜t＜11 D．2≤t＜6‎ ‎【解答】解：∵y＝x2+bx+3的对称轴为直线x＝1，‎ ‎∴b＝﹣2，‎ ‎∴y＝x2﹣2x+3，‎ ‎∴一元二次方程x2+bx+3﹣t＝0的实数根可以看做y＝x2﹣2x+3与函数y＝t的有交点，‎ ‎∵方程在﹣1＜x＜4的范围内有实数根，‎ 当x＝﹣1时，y＝6；‎ 当x＝4时，y＝11；‎ 函数y＝x2﹣2x+3在x＝1时有最小值2；‎ ‎∴2≤t＜11；‎ 故选：A．‎ 二、填空题（本题共6小题，满分18分。只要求填写最后结果，每小题填对得3分。）‎ ‎13．（3分）若2x＝3，2y＝5，则2x+y＝　15　．‎ ‎【解答】解：∵2x＝3，2y＝5，‎ ‎∴2x+y＝2x•2y＝3×5＝15．‎ 故答案为：15．‎ ‎14．（3分）当直线y＝（2﹣2k）x+k﹣3经过第二、三、四象限时，则k的取值范围是　1＜k＜3　．‎ ‎【解答】解：y＝（2﹣2k）x+k﹣3经过第二、三、四象限，‎ ‎∴2﹣2k＜0，k﹣3＜0，‎ ‎∴k＞1，k＜3，‎ ‎∴1＜k＜3；‎ 故答案为1＜k＜3；‎ ‎15．（3分）如图，Rt△AOB中，∠AOB＝90°，顶点A，B分别在反比例函数y‎=‎‎1‎x（x＞0）与y‎=‎‎-5‎x（x＜0）的图象上，则tan∠BAO的值为　‎5‎　．‎ ‎【解答】解：过A作AC⊥x轴，过B作BD⊥x轴于D，‎ 则∠BDO＝∠ACO＝90°，‎ ‎∵顶点A，B分别在反比例函数y‎=‎‎1‎x（x＞0）与y‎=‎‎-5‎x（x＜0）的图象上，‎ ‎∴S△BDO‎=‎‎5‎‎2‎，S△AOC‎=‎‎1‎‎2‎，‎ ‎∵∠AOB＝90°，‎ ‎∴∠BOD+∠DBO＝∠BOD+∠AOC＝90°，‎ ‎∴∠DBO＝∠AOC，‎ ‎∴△BDO∽△OCA，‎ ‎∴S‎△BODS‎△OAC‎=‎（OBOA）2‎=‎5‎‎2‎‎1‎‎2‎=‎5，‎ ‎∴OBOA‎=‎‎5‎，‎ ‎∴tan∠BAO‎=OBOA=‎‎5‎，‎ 故答案为：‎5‎．‎ ‎16．（3分）如图，在矩形ABCD中，AD＝2．将∠A向内翻折，点A落在BC上，记为A′，折痕为DE．若将∠B沿EA′向内翻折，点B恰好落在DE上，记为B′，则AB＝　‎3‎　．‎ ‎【解答】解：∵四边形ABCD为矩形，‎ ‎∴∠ADC＝∠C＝∠B＝90°，AB＝DC，‎ 由翻折知，△AED≌△A'ED，△A'BE≌△A'B'E，∠A'B'E＝∠B＝∠A'B'D＝90°，‎ ‎∴∠AED＝∠A'ED，∠A'EB＝∠A'EB'，BE＝B'E，‎ ‎∴∠AED＝∠A'ED＝∠A'EB‎=‎1‎‎3‎×‎180°＝60°，‎ ‎∴∠ADE＝90°﹣∠AED＝30°，∠A'DE＝90°﹣∠A'EB＝30°，‎ ‎∴∠ADE＝∠A'DE＝∠A'DC＝30°，‎ 又∵∠C＝∠A'B'D＝90°，DA'＝DA'，‎ ‎∴△DB'A'≌△DCA'（AAS），‎ ‎∴DC＝DB'，‎ 在Rt△AED中，‎ ‎∠ADE＝30°，AD＝2，‎ ‎∴AE‎=‎2‎‎3‎=‎‎2‎‎3‎‎3‎，‎ 设AB＝DC＝x，则BE＝B'E＝x‎-‎‎2‎‎3‎‎3‎ ‎∵AE2+AD2＝DE2，‎ ‎∴（‎2‎‎3‎‎3‎）2+22＝（x+x‎-‎‎2‎‎3‎‎3‎）2，‎ 解得，x1‎=-‎‎3‎‎3‎（负值舍去），x2‎=‎‎3‎，‎ 故答案为：‎3‎．‎ ‎17．（3分）如图，直线y＝x+1与抛物线y＝x2﹣4x+5交于A，B两点，点P是y轴上的一个动点，当△PAB的周长最小时，S△PAB＝　‎12‎‎5‎　．‎ ‎【解答】解：y=x+1‎y=x‎2‎-4x+5‎，‎ 解得，x=1‎y=2‎或x=4‎y=5‎，‎ ‎∴点A的坐标为（1，2），点B的坐标为（4，5），‎ ‎∴AB‎=‎(5-2‎)‎‎2‎+(4-1‎‎)‎‎2‎=‎3‎2‎，‎ 作点A关于y轴的对称点A′，连接A′B与y轴的交于P，则此时△PAB的周长最小，‎ 点A′的坐标为（﹣1，2），点B的坐标为（4，5），‎ 设直线A′B的函数解析式为y＝kx+b，‎ ‎-k+b=2‎‎4k+b=5‎‎，得k=‎‎3‎‎5‎b=‎‎13‎‎5‎，‎ ‎∴直线A′B的函数解析式为y‎=‎‎3‎‎5‎x‎+‎‎13‎‎5‎，‎ 当x＝0时，y‎=‎‎13‎‎5‎，‎ 即点P的坐标为（0，‎13‎‎5‎），‎ 将x＝0代入直线y＝x+1中，得y＝1，‎ ‎∵直线y＝x+1与y轴的夹角是45°，‎ ‎∴点P到直线AB的距离是：（‎13‎‎5‎‎-‎1）×sin45°‎=‎8‎‎5‎×‎2‎‎2‎=‎‎4‎‎2‎‎5‎，‎ ‎∴△PAB的面积是：‎3‎2‎×‎‎4‎‎2‎‎5‎‎2‎‎=‎‎12‎‎5‎，‎ 故答案为：‎12‎‎5‎．‎ ‎18．（3分）如图所示，在平面直角坐标系xoy中，一组同心圆的圆心为坐标原点O，它们的半径分别为1，2，3，…，按照“加1”依次递增；一组平行线，l0，l1，l2，l3，…都与x轴垂直，相邻两直线的间距为l，其中l0与y轴重合若半径为2的圆与l1在第一象限内交于点P1，半径为3的圆与l2在第一象限内交于点P2，…，半径为n+1的圆与ln在第一象限内交于点Pn，则点Pn的坐标为　（n，‎2n+1‎）　．（n为正整数）‎ ‎【解答】解：连接OP1，OP2，OP3，l1、l2、l3与x轴分别交于A1、A2、A3，如图所示：‎ 在Rt△OA1P1中，OA1＝1，OP1＝2，‎ ‎∴A1P1‎=OP‎1‎‎2‎-OA‎1‎‎2‎=‎2‎‎2‎‎-‎‎1‎‎2‎=‎‎3‎，‎ 同理：A2P2‎=‎3‎‎2‎‎-‎‎2‎‎2‎=‎‎5‎，A3P3‎=‎4‎‎2‎‎-‎‎3‎‎2‎=‎‎7‎，……，‎ ‎∴P1的坐标为（ 1，‎3‎），P2的坐标为（ 2，‎5‎），P3的坐标为（3，‎7‎），……，‎ ‎…按照此规律可得点Pn的坐标是（n，‎(n+1‎)‎‎2‎-‎n‎2‎），即（n，‎2n+1‎）‎ 故答案为：（n，‎2n+1‎）．‎ 三、解答题（本题共7小题，共66分。解答应写出文字说明、证明过程或推演步骤。）‎ ‎19．（5分）己知关于x，y的二元一次方程组‎2x-3y=5‎x-2y=k的解满足x＞y，求k的取值范围．‎ ‎【解答】解：‎‎2x-3y=5①‎x-2y=k②‎ ‎①﹣②得：x﹣y＝5﹣k，‎ ‎∵x＞y，‎ ‎∴x﹣y＞0．‎ ‎∴5﹣k＞0．‎ 解得：k＜5．‎ ‎20．（6分）自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多，为方便群众步行健身，某地政府决定对一段如图1所示的坡路进行改造．如图2所示，改造前的斜坡AB＝200米，坡度为1：‎3‎；将斜坡AB的高度AE降低AC＝20米后，斜坡AB改造为斜坡CD，其坡度为1：4．求斜坡CD的长．（结果保留根号）‎ ‎【解答】解：∵∠AEB＝90°，AB＝200，坡度为1：‎3‎，‎ ‎∴tan∠ABE‎=‎1‎‎3‎=‎‎3‎‎3‎，‎ ‎∴∠ABE＝30°，‎ ‎∴AE‎=‎‎1‎‎2‎AB＝100，‎ ‎∵AC＝20，‎ ‎∴CE＝80，‎ ‎∵∠CED＝90°，斜坡CD的坡度为1：4，‎ ‎∴CEDE‎=‎‎1‎‎4‎，‎ 即‎80‎ED‎=‎‎1‎‎4‎，‎ 解得，ED＝320，‎ ‎∴CD‎=‎8‎0‎‎2‎+32‎‎0‎‎2‎=80‎‎17‎米，‎ 答：斜坡CD的长是‎80‎‎17‎米．‎ ‎21．（9分）如图所示，有一个可以自由转动的转盘，其盘面分为4等份，在每一等份分别标有对应的数字2，3，4，5．小明打算自由转动转盘10次，现已经转动了8次，每一次停止后，小明将指针所指数字记录如下：‎ 次数 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 第9次 第10次 数字 ‎3‎ ‎5‎ ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎3‎ ‎5‎ ‎（1）求前8次的指针所指数字的平均数．‎ ‎（2）小明继续自由转动转盘2次，判断是否可能发生“这10次的指针所指数字的平均数不小于3.3，且不大于3.5”的结果？若有可能，计算发生此结果的概率，并写出计算过程；若不可能，说明理由．（指针指向盘面等分线时为无效转次．）‎ ‎【解答】解：（1）前8次的指针所指数字的平均数为‎1‎‎8‎‎×‎（3+5+2+3+3+4+3+5）＝3.5；‎ ‎（2）∵这10次的指针所指数字的平均数不小于3.3，且不大于3.5，‎ ‎∴后两次指正所指数字和要满足不小于5且不大于7，‎ 画树状图如下：‎ 由树状图知共有16种等可能结果，其中符合条件的有9种结果，‎ 所以此结果的概率为‎9‎‎16‎．‎ ‎22．（10分）如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M．‎ ‎（1）求证：△AHF为等腰直角三角形．‎ ‎（2）若AB＝3，EC＝5，求EM的长．‎ ‎【解答】证明：（1）∵四边形ABCD，四边形ECGF都是正方形 ‎∴DA∥BC，AD＝CD，FG＝CG，∠B＝∠CGF＝90°‎ ‎∵AD∥BC，AH∥DG ‎∴四边形AHGD是平行四边形 ‎∴AH＝DG，AD＝HG＝CD ‎∵CD＝HG，∠ECG＝∠CGF＝90°，FG＝CG ‎∴△DCG≌△HGF（SAS）‎ ‎∴DG＝HF，∠HFG＝∠HGD ‎∴AH＝HF，‎ ‎∵∠HGD+∠DGF＝90°‎ ‎∴∠HFG+∠DGF＝90°‎ ‎∴DG⊥HF，且AH∥DG ‎∴AH⊥HF，且AH＝HF ‎∴△AHF为等腰直角三角形．‎ ‎（2）∵AB＝3，EC＝5，‎ ‎∴AD＝CD＝3，DE＝2，EF＝5‎ ‎∵AD∥EF ‎∴EMDM‎=EFAD=‎‎5‎‎3‎，且DE＝2‎ ‎∴EM‎=‎‎5‎‎4‎ ‎23．（10分）扶贫工作小组对果农进行精准扶贫，帮助果农将一种有机生态水果拓宽了市场．与去年相比，今年这种水果的产量增加了1000千克，每千克的平均批发价比去年降低了1元，批发销售总额比去年增加了20%．‎ ‎（1）已知去年这种水果批发销售总额为10万元，求这种水果今年每千克的平均批发价是多少元？‎ ‎（2）某水果店从果农处直接批发，专营这种水果．调查发现，若每千克的平均销售价为41元，则每天可售出300千克；若每千克的平均销售价每降低3元，每天可多卖出180千克，设水果店一天的利润为w元，当每千克的平均销售价为多少元时，该水果店一天的利润最大，最大利润是多少？（利润计算时，其它费用忽略不计．）‎ ‎【解答】解：‎ ‎（1）由题意，设这种水果今年每千克的平均批发价是x元，则去年的批发价为（x+1）元 今年的批发销售总额为10（1+20%）＝12万元 ‎∴‎‎120000‎x‎-‎100000‎x+1‎=1000‎ 整理得x2﹣19x﹣120＝0‎ 解得x＝24或x＝﹣5（不合题意，舍去）‎ 故这种水果今年每千克的平均批发价是24元．‎ ‎（2）设每千克的平均售价为m元，依题意 由（1）知平均批发价为24元，则有 w＝（m﹣24）（‎41-m‎3‎‎×‎180+300）＝﹣60m2+4200m﹣66240‎ 整理得w＝﹣60（m﹣35）2+7260‎ ‎∵a＝﹣60＜0‎ ‎∴抛物线开口向下 ‎∴当m＝35元时，w取最大值 即每千克的平均销售价为35元时，该水果店一天的利润最大，最大利润是7260元 ‎24．（13分）如图1，菱形ABCD的顶点A，D在直线上，∠BAD＝60°，以点A 为旋转中心将菱形ABCD顺时针旋转α（0°＜α＜30°），得到菱形AB′C′D′，B′C′交对角线AC于点M，C′D′交直线l于点N，连接MN．‎ ‎（1）当MN∥B′D′时，求α的大小．‎ ‎（2）如图2，对角线B′D′交AC于点H，交直线l与点G，延长C′B′交AB于点E，连接EH．当△HEB′的周长为2时，求菱形ABCD的周长．‎ ‎【解答】解：（1）∵四边形AB′C′D′是菱形，‎ ‎∴AB′＝B′C′＝C′D′＝AD′，‎ ‎∵∠B′AD′＝∠B′C′D′＝60°，‎ ‎∴△AB′D′，△B′C′D′是等边三角形，‎ ‎∵MN∥B′C′，‎ ‎∴∠C′MN＝∠C′B′D′＝60°，∠CNM＝∠C′D′B′＝60°，‎ ‎∴△C′MN是等边三角形，‎ ‎∴C′M＝C′N，‎ ‎∴MB′＝ND′，‎ ‎∵∠AB′M＝∠AD′N＝120°，AB′＝AD′，‎ ‎∴△AB′M≌△AD′N（SAS），‎ ‎∴∠B′AM＝∠D′AN，‎ ‎∵∠CAD‎=‎‎1‎‎2‎∠BAD＝30°，‎ ‎∠DAD′＝15°，‎ ‎∴α＝15°．‎ ‎（2）∵∠C′B′D′＝60°，‎ ‎∴∠EB′G＝120°，‎ ‎∵∠EAG＝60°，‎ ‎∴∠EAG+∠EB′G＝180°，‎ ‎∴四边形EAGB′四点共圆，‎ ‎∴∠AEB′＝∠AGD′，‎ ‎∵∠EAB′＝∠GAD′，AB′＝AD′，‎ ‎∴△AEB′≌△AGD′（AAS），‎ ‎∴EB′＝GD′，AE＝AG，‎ ‎∵AH＝AH，∠HAE＝∠HAG，‎ ‎∴△AHE≌△AHG（SAS），‎ ‎∴EH＝GH，‎ ‎∵△EHB′的周长为2，‎ ‎∴EH+EB′+HB′＝B′H+HG+GD′＝B′D′＝2，‎ ‎∴AB′＝AB＝2，‎ ‎∴菱形ABCD的周长为8．‎ ‎25．（13分）如图，在平面直角坐标系xoy中，O为坐标原点，点A（4，0），点B（0，4），△ABO的中线AC与y轴交于点C，且⊙M经过O，A，C三点．‎ ‎（1）求圆心M的坐标；‎ ‎（2）若直线AD与⊙M相切于点A，交y轴于点D，求直线AD的函数表达式；‎ ‎（3）在过点B且以圆心M为顶点的抛物线上有一动点P，过点P作PE∥y轴，交直线AD于点E．若以PE为半径的⊙P与直线AD相交于另一点F．当EF＝4‎5‎时，求点P的坐标．‎ ‎【解答】解：（1）点B（0，4），则点C（0，2），‎ ‎∵点A（4，0），则点M（2，1）；‎ ‎（2）∵⊙P与直线AD，则∠CAD＝90°，‎ 设：∠CAO＝α，则∠CAO＝∠ODA＝∠PEH＝α，‎ tan∠CAO‎=OCOA=‎1‎‎2‎=‎tanα，则sinα‎=‎‎1‎‎5‎，cosα‎=‎‎2‎‎5‎，‎ AC‎=‎‎10‎，则CD‎=ACsin∠CDA=‎10‎sinα=‎10，‎ 则点D（0，﹣8），‎ 将点A、D的坐标代入一次函数表达式：y＝mx+n并解得：‎ 直线AD的表达式为：y＝2x﹣8；‎ ‎（3）抛物线的表达式为：y＝a（x﹣2）2+1，‎ 将点B坐标代入上式并解得：a‎=‎‎3‎‎4‎，‎ 故抛物线的表达式为：y‎=‎‎3‎‎4‎x2﹣3x+4，‎ 过点P作PH⊥EF，则EH‎=‎‎1‎‎2‎EF＝2‎5‎，‎ cos∠PEH‎=EHPE=‎2‎‎5‎PE=cosα=‎‎2‎‎5‎，‎ 解得：PE＝5，‎ 设点P（x，‎3‎‎4‎x2﹣3x+4），则点E（x，2x﹣8），‎ 则PE‎=‎‎3‎‎4‎x2﹣3x+4﹣2x+8＝5，‎ 解得x‎=‎‎14‎‎3‎或2，‎ 则点P（‎14‎‎3‎，‎19‎‎3‎）或（2，1）．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:56:34；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎