比例的基本性质黄金分割教案(2) 2页

课题 比例的基本性质黄金分割 第 1 课时 总序第 　 个教案 课型 新授 编写时间 年 月 日 执行时间 年 月 日 教学目标 ‎1、进一步巩固比例的有关性质，培养学生解决问题的能力。‎ ‎2、了解黄金分割。‎ ‎3、此外，通过黄金分割的内容的学习，联系工厂普遍应用的“0.618法”，让学生真正体会到数学来源于实践，数学服务于生产，使学生更喜欢数学 。‎ 教学重点 比例的性质应用 教学难点 黄金分割的意义 教学用具 幻灯、三角尺 教学方法 自学、合作探究、练习与讲授相结合 教学过程 一、复习引入：‎ ‎⑴、已知：如图5－6，点C、D在线段AB上，AC∶CD=CD∶DB，且AC=2.5cm，DB=10cm，则CD= cm，AB= cm，CD是线段 和 的比例中项。‎ ‎⑵、若已知线段AC是线段AB、BC的比例中项，请用式子表示出来。‎ ‎⑶、说出比例的有关性质。‎ 二、新授：‎ 一、阅读课本 第207－208页 ，思考并回答下列问题：‎ ‎1、如图5－4，把AB分成两条线段AC和BC（AC＞BC），且使 是 比例中项，叫做把线段AB黄金分割， 叫做 黄金分割点。‎ ‎2、已知AC＝AB≈0.618AB，则点C是AB的黄金分割点。‎ ‎3、长为1的线段的黄金分割点，大约在距一个端点的 处。‎ 二、例题评析： ‎ 例2：已知：如图5－4，AB=1，AC＝。求证：。‎ 例3：已知：线段AB=10cm，点C是AB的黄金分割点，且AC＞BC，求AC和BC的长。‎ 课堂练习：课本例5后练习第1、2、3题 ‎ 三、巩固练习 ‎1、填空： ‎ ‎1）已知：a、b、c为△ABC的三边，并且a+b+c=60cm,，则△ABC的面积为 。‎ ‎2）把长为10cm的线段黄金分割，则较短的线段的长是 ‎ 2‎ ‎3）若c是线段a、b的比例中项，a=4,b=9,那么，2a、b、的第四比例项是 。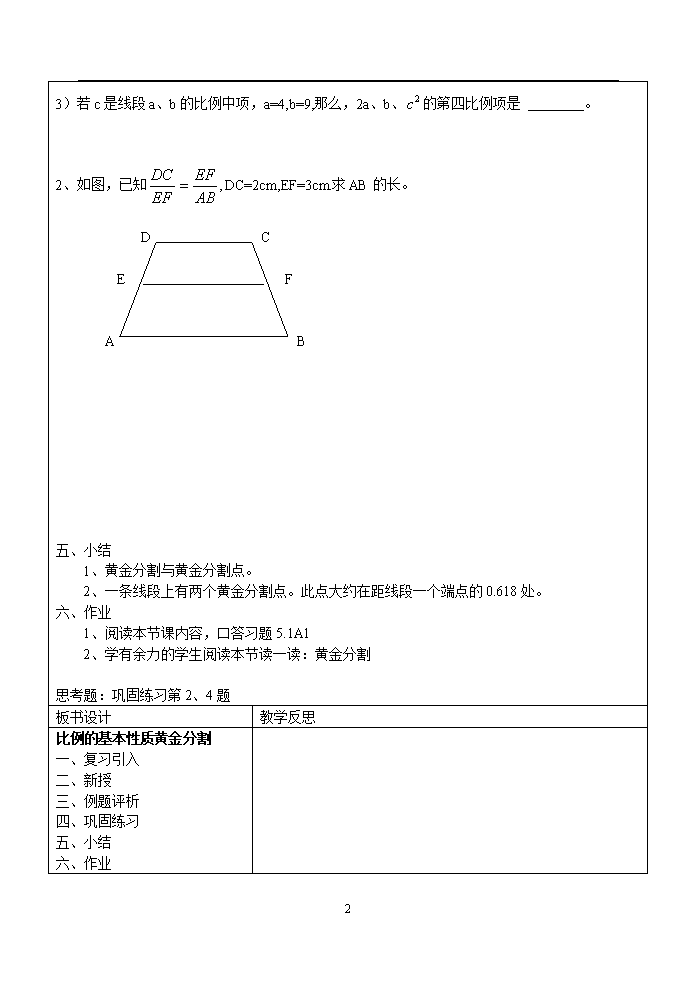‎ ‎ ‎ ‎2、如图，已知DC=2cm,EF=3cm.求AB的长。‎ ‎ ‎A D C B E F 五、小结 ‎1、黄金分割与黄金分割点。‎ ‎2、一条线段上有两个黄金分割点。此点大约在距线段一个端点的0.618处。‎ 六、作业 ‎1、阅读本节课内容，口答习题5.1A1‎ ‎2、学有余力的学生阅读本节读一读：黄金分割 ‎ ‎ 思考题：巩固练习第2、4题 板书设计 教学反思 比例的基本性质黄金分割 一、复习引入 二、新授 三、例题评析 四、巩固练习 五、小结 六、作业 2‎