中考数学一轮复习知识点+题型专题讲义06 二元一次方程（组）（教师版） 25页

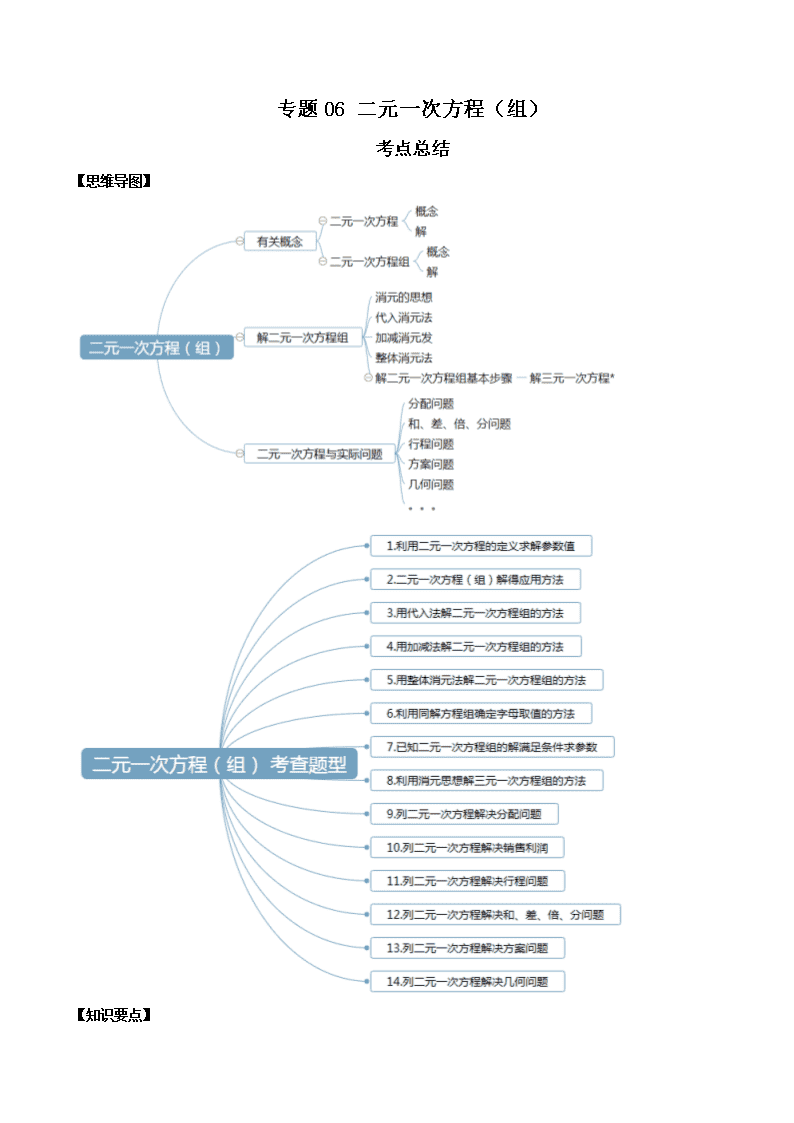
专题 06 二元一次方程（组） 考点总结 【思维导图】 【知识要点】 知识点一 二元一次方程（组）有关概念 二元一次方程的概念：含有两个未知数，并且未知数的项的次数都是 1，像这样的方程叫做二元一次方程。 【注意】 1） 二元：含有两个未知数； 2）一次：所含未知数的项的次数都是 1。 例如：xy=1，xy 的次数是二，属于二元二次方程。 2） 方程：方程的左右两边必须都是整式（分母不能出现未知数）。 二元一次方程的解：一般地，使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解． 【注意】 1） 在二元一次方程中，给定其中一个未知数的值，就可以求出另一个未知数的值。 2） 二元一次方程有无数个解，满足二元一次方程使得方程左右相等都是这个方程的解，但并不是说任意一 对数值就是它的解。 二元一次方程组的概念：含有两个未知数的两个一次方程所组成的一组方程，叫做二元一次方程组． 【注意】 1）二元一次方程组的“二元”和“一次”都是针对整个方程组而言的，组成方程组的各个方程不必同时含有两 个未知数，如 2x＋1＝0， x＋2y＝2 也是二元一次方程组。这两个一次方程不一定都是二元一次方程，但这两个一 次方程必须一共含有两个未知数。 3） 方程组中的各个方程中，相同字母必须代表同一未知量。 4） 二元一次方程组中的各个方程应是整式方程。 二元一次方程组的解：一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解。 【注意】 1）二元一次方程组的解是方程中每个方程的解。 2）一般情况下二元一次方程组的解是唯一的，但是有的方程组有无数个解或无解。 如： x＋y＝5， 4x＋4y＝20. 有的方程组无解，如： x＋y＝5， x＋y＝2. 【典型例题】 1．（2019·天津中考模拟）方程组 1 2 5 x y x y      的解是（ ） A． 1 2 x y     B． 2 1 x y     C． 1 2 x y    D． 2 1 x y    【答案】D 【解析】 A． 1 2 x y     不满足方程组 1 2 5 x y x y      ，故不符合题意；B， 2 1 x y     不满足方程组 1 2 5 x y x y      ，故不符 合题意；C， 1 2 x y    不满足方程组 1 2 5 x y x y      ，故不符合题意；D， 2 1 x y    满足方程组 1 2 5 x y x y      ，故符 合题意，故选 D． 2．（2019·湖北中考真题）把一根长 9m 的钢管截成 1m 长和 2m 长两种规格均有的短钢管，且没有余料，设 某种截法中 1m 长的钢管有 a 根，则 a 的值可能有（ ） A．3 种 B．4 种 C．5 种 D．9 种 【答案】B 【详解】 解：设 2m 的钢管b 根，根据题意得： 2 9a b  ， a 、b 均为整数， 1 4 a b   ， 3 3 a b    ， 5 2 a b    ， 7 1 a b    ． 故选：B． 考查题型一 利用二元一次方程的定义求解参数值 1．（2017·山东中考模拟）已知关于 x、y 的方程 2 2 1 6m n m nx y     是二元一次方程，则 m、n 的值为（ ） A．m=1，n=-1 B．m=-1,n=1 C．m= 1 3 ,n= 4 3  D．m= 1 3  ，n= 4 3 【答案】A 【详解】 ∵方程 2 2 14 6m n m nx y     是二元一次方程，∴ 2 3 0 m n m n      ，解得： 1 1 m n     ．故选 A． 2．（2016·贵州中考真题）已知关于 的方程 是二元一次方程，则 的值为（ ） A． B． 【【详解 【答案】D A．4 B．2 C．1 D．0 ，则 m n 的值为（ ）    y x 2 的解是 0      x ny m mx y n 2 2．（2019·辽宁中考真题）关于 x，y 的二元一次方程组 故选 C 解得：m=2. 将 x=4，y=2 代入方程组得：4m+2=10， 【解析】 【答案】C A．3 B．-3 C．2 D．-2 ，则 m 的值是（ ）    y x 2   的解是 4   x y mx y 1．（2017·湖北中考模拟）方程组 10{ 6 考查题型二 二元一次方程（组）解得应用方法 故选 B. 解这个方程组得 a=3，b=2． ＝ ， ＝    a b a b 1{ 4 1 【解析】试题解析：依题意，得 【答案】B A．3、1 B．3、2 C．2、1 D．2、-1 3．（2017·江苏中考模拟）如果 42 10a b a bx y    是二元一次方程，那么 a 、b 的值分别是( ) 解得：m=1，n=-1. ， 뀰 ൅ 삸 ൅ 灰 ٍ 灰 灰 ٍ ذ 삸 ذ 뀰 二元一次方程是指含有两个未知数，且未知数的次数都是一次的整式方程，依题意，有： 【解析】 【答案】A C． D． 解：把 0 2 x y    代入得： 2 2 2 n n m    ，解得： 2 2 m n     ，∴ 0m n  ， 故选：D． 3．（2012·山东中考真题）关于 x、y 的方程组 3{ x y m x my n     的解是 1 1 x y    ，则 m n 的值是（ ） A．5 B．3 C．2 D．1 【答案】D 【详解】 解：∵方程组 3x y m x my n     的解是 1 1 x y   ， ∴ 3 1 1 m m n      解得 2 3 m n    所以，|m-n|=|2-3|=1． 故选 D． 4．（2012·山东中考真题）已知 =2{ =1 x y 是二元一次方程组 + =8{   =1 mx ny nx my 的解，则 2m n 的算术平方根为（ ） A．±2 B． C．2 D．4 【答案】C 【解析】 ∵ =2{ =1 x y 是二元一次方程组 + =8{   =1 mx ny nx my 的解，∴ 2 + =8{2 =1 m n n m ，解得 =3{ =2 m n 。 ∴ 2 = 2 3 2= 4=2m n   。即 2m n 的算术平方根为 2。故选 C。 知识点二 解二元一次方程组 消元的思想：二元一次方程组中有两个未知数，如果消去其中一个未知数，将二元一次方程组转化为熟悉 的一元一次方程，即可先求出一个未知数，然后再求另一个未知数。这种将未知数的个数由多化少、逐一 解决的思想，叫做消元的思想。 代入消元法：把二元一次方程组中一个方程的未知数用含另一个未知数的式子表示出来，再代入另一个方 程，实现消元，进而求得这个二元一次方程组的解。这个方法叫做代入消元法，简称代入法。 基本思路：未知数由多变少。 代入消元法解二元一次方程组的一般步骤： 1.变：将其中一个方程变形，使一个未知数用含有另一个的未知数的代数式表示。 2.代：用这个代数式代替另一个方程中的相应未知数，得到一元一次方程。 3.解：解一元一次方程 4.求：把求得的未知数的值带入代数式或原方程组中的任意一个方程中，求得另一个未知数的值。 5.写：写出方程组的解。 6.验：将方程组的解带入到原方程组中的每个方程中，若各方程均成立，则这对数值就是原方程组的解，负 责解题有误。 考查题型三 用代入法解二元一次方程组的方法 1．（2019·北京中考模拟）二元一次方程组 2 2 4 x y x y      的解是 ( ) A． 0 2 x y    B． 2 0 x y    C． 3 1 x y     D． 1 1 x y    【答案】B 【详解】 2 2 4 x y x y      ① ② ， ①+②得：3x=6，即 x=2， 把 x=2 代入①得：y=0， 则方程组的解为 2 0 x y    ， 故答案选 B. 2．（2019·丹东市第十四中学中考模拟）以方程组 2 1 y x y x       的解为坐标的点(x，y)在平面直角坐标系中的 位置是( ) A．第一象限 B．第二象限 C．第三象限 D．第四象限 【答案】A 【解析】 2 , 1 . y x y x       ① ② ， ①+②得，2y=1， 解得,y= 1 2 . 把 y= 1 2 代入①得, 1 2 =−x+2， 解得 x= 3 2 . ∵ 3 2 >0, 1 2 >0，根据各象限内点的坐标特点可知， 点(x,y)在平面直角坐标系中的第一象限。 故选：A. 3．（2017·内蒙古中考模拟）已知一个等腰三角形的两边长 x，y 满足方程组 2 3{3 2 8 x y x y     ，则此等腰三角形 的周长为（ ） A．5 B．4 C．3 D．5 或 4 【答案】A 【解析】 先解二元一次方程组 2 3 3 2 8 x y x y      ,解得 2 1 x y    ,所以等腰三角形的两边长为 2,1.若腰长为 1,底边长为 2,由三 角形三边关系可知这样的三角形不存在,若腰长为 2,底边长为 1,根据三边关系可知可以构成三角形,所以这个 等腰三角形的周长为 5. 加减消元法：两个二元一次方程中同一个未知数的系数相反或相等时，把这两个方程的两边分别相加或相 减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法，简称加减法。 加减消元法解二元一次方程组的一般步骤： 1.变形：将两个方程中其中一个未知数的系数化为相同（或互为相反数）。 2.加减：通过相减（或相加）消去这个未知数，得到一个一元一次方程。 3.求解：解这个一元一次方程，得到一个未知数的值。 4.回代：将求得的未知数的值代入原方程组中的任意一个方程，求出另一个未知数的值。 ．故选 B 则 a+b=4， ①+②：4a+4b=16 ， ͷ ٍ e ذ ൅ ͷ ٍ 灰 试题解析： 【解析】 【答案】B A．﹣4 B．4 C．﹣2 D．2 则 a+b 的值为（ ） ͷ ٍ e ذ ൅ ͷ ٍ 灰 2．（2019·广东华南师大附中中考模拟）已知 a，b 满足方程组 故选：D． ．    y x 1 ∴方程组的解为 1 把 x=1 代入①得，3-2y=1，解得 y=1， ①+②×2 得，5x=5，解得 x=1， ② ， ①    x y x y =2 将方程组变形为 3 2 =1 ＝ ＝      x y x y 2 0 ∴ 3 2 1 0 ∵ 3 2 1 2 0x y x y      ， 【解析】 【答案】D    y x 1 D． 1    y x 2 C． 0    y x 0 B． 2    y x 4 A． 1 1．（2018·广西中考真题）若| 3 2 1| 2 0x y x y      ，则 x，y 的值为（ ） 考查题型四 用加减法解二元一次方程组的方法 负责解题有误。 6.检验：将方程组的解带入到原方程组中的每个方程中，若各方程均成立，则这对数值就是原方程组的解， 写解：写出方程组的解。.5 3．（2019·黑龙江中考模拟）由方程组 + =4 3 x m y m     可得出 x 与 y 之间的关系是( )． A．x＋y＝1 B．x＋y＝－1 C．x＋y＝7 D．x＋y＝－7 【答案】C 【详解】 原方程可化为 4 3 x m y m ＝ ① ＝ ②    ， ①+②得，x+y=7． 故选 C． 整体消元法：根据方程组各系数的特点，可将方程组中的一个方程或方程的一部分看成一个整体，带入另 一个方程中，从而达到消去其中一个未知数的目的，并求得方程的解。 例         5 4 8 5 4 4 x y x y           令 x+5=m，y-4=n 原方程可写为 8 m 4 m n n        解得 m=6，n=2，所以 x+5=6,y-4=2， 所以 1 6 x y      特点：两方程中都含有相同的代数式，如题中的 x+5,y-4 之类，换元后可简化方程也是主要原因。 考查题型五 用整体消元法解二元一次方程组的方法 1．（2017·浙江中考真题）若二元一次方程组 的解为 则 （ ） A． B． C． D． 【答案】D 【解析】 ∵x+y=3，3x-5y=4， ∴两式相加可得：（x+y）+（3x-5y）=3+4， ∴4x-4y=7， ∴x-y= ， ∵x=a，y=b， ∴a-b=x-y= 故选 D. 2．（2018·河北中考模拟）若方程组 2 3 7 3 5 1 m n m n      的解是 2 1 m n     ，则方程组         2 1 3 2 7 3 1 5 2 1 x y x y          的解 是（ ） A． 1 1 x y    B． 1 1 x y     C． 3 1 x y    D． 3 3 x y     【答案】A 【解析】 解：令 x+1=m，y﹣2=n，∴方程组 2 1 3 2 7 3 1 5 2 1 x y x y          （ ） （ ） （ ） （ ） 可化为 2 3 7 3 5 1 m n m n      ．∵方程组 2 3 7 3 5 1 m n m n      的 解是 2 1 m n     ，∴x+1=2，y﹣2=﹣1，解得： 1 1 x y    ．故选 A． 考查题型六 利用同解方程组确定字母取值的方法 1．（2019·杭州绿城育华学校中考模拟）若关于 x，y 的二元一次方程组 5 9 x y k x y k      的解也是二元一次方程 2x+3y＝6 的解，则 k 的值为（ ） A． 3 4 B． 4 3 C．﹣ 3 4 D．﹣ 4 3 【答案】A 【详解】 解： 5 9 x y k x y k      ① ② ， ①+②得：2x＝14k， 解得：x＝7k， ①﹣②得：2y＝﹣4k， 解得：y＝﹣2k， 把 x＝7k，y＝﹣2k 代入方程得：14k﹣6k＝6， 解得：k＝ 3 4 ， 故选：A． 2．（2018·天津中考模拟）已知关于 x，y 的方程组 2 3 4 2 x y ax by      ，与 3 5 6 4 x y bx ay       ，有相同的解，则 a， b 的值为（ ） A． 2 1 a b     B． 1 2 a b     C． 1 2 a b    D． 1 2 a b      【答案】B 【解析】 关于 x,y 的方程组 2 3 4 2 x y ax by      与 3 5 6 4 x y bx ay       ,有相同的解,所以 2 3 4 3 5 6 x y x y      ,解得 2 0 x y    ,将 2 0 x y    代 入 2 4 ax by bx ay       可得 2 2 2 4 a b     ,解得 1 2 a b     ,故选 B. 3.（2015·广东中考模拟）方程 5x＋2y＝－9 与下列方程构成的方程组的解为 2 1 2 x y    的是( ) A．x＋2y＝1 B．3x＋2y＝－8 C．5x＋4y＝－3 D．3x－4y＝－8 【答案】D 【解析】 解：方程 5x+2y=﹣9 与下列方程构成的方程组的解为 的是 3x﹣4y=﹣8． 故选 D． 4．（2019·河北中考模拟）关于 x、y 的方程组 2 3 9 x y m x y m      的解是方程 3x+2y＝34 的一组解，那么 m 的值 是( ) A．﹣2 B．﹣1 C．1 D．2 【答案】D 【详解】 2 3 9 x y m x y m      ① ② ， ①﹣②得，3y＝﹣6m， 解得，y＝﹣2m， 把 y＝﹣2m 代入②得，x＝7m， 由题意得，3×7m﹣2×2m＝34， 解得，m＝2， 故选：D． 5．（2019·江苏中考模拟）关于 x，y 的方程组 3 2 2 x y x y k       的解满足 x＝y，则 k 的值是（ ） A．﹣1 B．0 C．1 D．2 【答案】B 【详解】 解方程组 3 2 2 x y x y k       得： 4 4 3 34 kx ky      ， ∵x＝y， ∴ k 4 3k 14 4    ， 解得：k＝0． 故选 B． 6．（2019·北京青云店中学中考模拟）若方程 x﹣y＝﹣1 的一个解与方程组 2 2 1 x y k x y      的解相同，则 k 的值 为_____． 【答案】-4 【详解】 （ ）解为 2x y   ，则 m 的最小整数 的解满足 3        x y m x y 2 3 2 1．（2019·山东中考模拟）若关于 x，y 的方程组 2 4 考查题型七 已知二元一次方程组的解满足条件求参数 故答案为：6． 则 mn=6， ， 灰 ＝ 삸 灰 ＝ 뀰 解得： ， ذ 삸 ＝ 灰 灰 ＝ 뀰 得：， ذ 삸 ＝ 삸͵ ذ ݔ 灰 ＝ 뀰ݔ ൅ 삸͵ 将 x=2、y=0 代入 ， ＝ ͵ ＝ ݔ 则 解得：y=0， 将 x=2 代入①，得：6-y=6， 解得：x=2， ①×2+②，得：10x=20， ， ＝ eݔ ൅ ͵ ͳ ＝ ͵ ذ ݔ 联立得： 【详解】 【答案】6 的解， 则 mn 的值为_____． 有相同 eݔ ൅ ͵ ٍ ذ 삸͵ ٍ 삸 ذ ݔ 与 ͳ ٍ ͵ ذ ݔ 뀰ݔ ൅ 삸͵ ٍ 灰 7．（2018·江苏中考模拟）若两个关于 x，y 的二元一次方程组 故答案为﹣4 解得：k＝﹣4， 代入方程得：2﹣6＝k， ，    y x 3 解得： 2 ，       x y x y 2 1 解：联立方程得： 1 A．﹣3 B．﹣2 C．﹣1 D．0 【答案】B 【详解】 解： 2 4 2 3 2 x y x y m      ＝ ① ＝ ② ， ①-②得：x-y=3m+2， ∵关于 x，y 的方程组 2 4 2 3 2 x y x y m      ＝ ＝ 的解满足 x-y＞- 3 2 ， ∴3m+2＞- 3 2 ， 解得：m＞ 7 6  ， ∴m 的最小整数解为-1， 故选 B． 2．（2017·广东中考模拟）已知方程组 3 1 3 2 x y m x y m       的解 x，y 满足 x+2y≥0，则 m 的取值范围是 （ ）. A．m≥ 1 3 B． 1 3 ≤m≤1 C．m≤1 D．m≥-1 【答案】C 【解析】 详解： 3 1 3 2 x y m x y m       ① ②， ①-②，得 2 4 1 ,x y m   12 ,2 mx y   2 0,x y  1 0,2 m  解得： 1.m  故选 C. 3．（2018·江苏中考模拟）已知 x 2y 4k{2x y 2k 1      ，且 1 x y 0    ，则 k 的取值范围为 A． 11 k 2     B． 10 k 2   C． 0 k 1  D． 1 k 12   【答案】D 【详解】 ∵ x+2y=4k 2x+y=2k+1    ① ② ∴②－①，得 x y 2k 1    将 x y 2k 1    代入 1 x y 0    ，得： 11 2k 1 0 2 2k 1 k 12               故选 D 4.（2018·江苏中考模拟）方程组 2 1 2 1 x y a x y a        的解 x、y 满足不等式 2x﹣y＞1，则 a 的取值范围为（ ） A．a≥ 1 2 B．a＞ 1 3 C．a≤ 2 3 D．a＞ 3 2 【答案】B 【详解】 2 1 2 1 x y a x y a        ① ② ①+②得： 2 - 3 1x y a  ， 解得： 1 3a  ． 故选：B． 解二元一次方程的基本步骤： 1.消元 2.求解 3.回代 4.写解 5.检验 解三元一次方程的基本步骤 1.变形（变三元一次为二元一次） 2.求解：解二元一次方程组 3.回代：将求得的未知数的值代入原方程组的一个适当的方程中，得到一个一元一次方程 4.求解：解一元一次方程，求出第三个未知数 5.写解：用大括号将所求的的三个未知数的值联立起来，即得原方程组的解。 考查题型八 利用消元思想解三元一次方程组的方法 1．（2018·江苏中考模拟）已知 4 3 3 0{ 3 0 x y z x y z       ，那么 x：y：z 为（ ） A．2：（﹣1）：3 B．6：1：9 C．6：（﹣1）：9 D． 2 1: :13 9     【答案】C 【解析】 方程组整理得： 4 3 3 3 x y z x y z    ＝ ① ＝ ② , ①-②得：3x=2z，即 x= 2 3 z， 将 x= 2 3 z 代入②得：y=- 1 9 z， 则 x：y：z= 2 3 z：（- 1 9 z）：z=6：（-1）：9． 故选 C． 2．（2017·四川中考模拟）三元一次方程组 的解为（ ） A． B． C． D． 【答案】C 【解析】 解方程组得 C. 知识点三 列二元一次方程组解应用题 列二元一次方程组解应用题的一般步骤： 1. 审：审题，明确各数量之间的关系。 2. 设：设未知数 3. 找：找题中的等量关系 4. 列：根据等量关系列出两个方程，组成方程组 5. 解：解方程组，求出未知数的值 6. 答：检验方程组的解是否符合题意，写出答案。 考查题型九 列二元一次方程解决分配问题 1．（2019·浙江中考模拟）某旅店一共 70 个房间，大房间每间住 8 个人，小房间每间住 6 个人，一共 480 个学生刚好住满，设大房间有 x 个，小房间有 y 个.下列方程正确的是( ) A． 70 8 6 480 x y x y      B． 70 6 8 480 x y x y      C． 480 6 8 70 x y x y      D． 480 8 6 70 x y x y      【答案】A 【详解】大房间有 x 个，小房间有 y 个， 由题意得： 70 8 6 480 x y x y      ， 故选 A. 2．（2018·河南中考真题）《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三,问人 数、羊价各几何？”其大意是：今有人合伙买羊，若每人出 5 钱，还差 45 钱；若每人出 7 钱，还差 3 钱， 问合伙人数、羊价各是多少？设合伙人数为 x 人，羊价为 y 钱，根据题意，可列方程组为（ ） A． 5 45 7 3 y x y x      B． 5 45 7 3 y x y x      C． 5 45 7 3 y x y x      D． 5 45 7 3 y x y x      【答案】A 【解析】 设合伙人数为 x 人，羊价为 y 钱，根据题意，可列方程组为： 5 45 7 3 y x y x      ． 故选 A． 3．（2018·湖北中考真题）我国古代数学著作《九章算术》卷七有下列问题：“今有共买物，人出八，盈三： 人出七，不足四，问人数、物价几何？”意思是：现在有几个人共同出钱去买件物品，如果每人出 8 钱，则 剩余 3 钱：如果每人出 7 钱，则差 4 钱．问有多少人，物品的价格是多少？设有 x 人，物品的价格为 y 元， 可列方程（组）为（ ） A． 8 3 7 4 x y x y      B． 8 3 7 4 x y x y      C． 3 4 8 7 x x  D． 3 4 8 7 y y  【答案】A 【详解】 设有 x 人，物品的价格为 y 元， 根据题意，可列方程： 8 3 7 4 x y x y      ， 故选 A． 考查题型十 列二元一次方程解决销售利润 1．（2018·山东中考真题）夏季来临，某超市试销 A 、 B 两种型号的风扇，两周内共销售 30 台，销售收入 5300 元， A 型风扇每台 200 元， B 型风扇每台 150 元，问 A 、 B 两种型号的风扇分别销售了多少台？若设 A 型风扇销售了 x 台， B 型风扇销售了 y 台，则根据题意列出方程组为（ ） A． 5300 200 150 30 x y x y      B． 5300 150 200 30 x y x y      C． 30 200 150 5300 x y x y      D． 30 150 200 5300 x y x y      【答案】C 【解析】 设 A 型风扇销售了 x 台，B 型风扇销售了 y 台，则根据题意列出方程组为： 30 200 150 5300 x y x y      ． 故选 C． 2．（2018·山东中考模拟）为了迎接体育中考，体育委员到体育用品商店购买排球和实心球，若购买 2 个排 球和 3 个实心球共需 95 元，若购买 5 个排球和 7 个实心球共需 230 元，若设每个排球 x 元，每个实心球 y 元，则根据题意列二元一次方程组得（ ） A． 3 2 95 5 7 230 x y x y      B． 2 3 95 5 7 230 x y x y      C． 3 2 95 7 5 230 x y x y      D． 2 3 95 7 5 230 x y x y      【答案】B 【解析】 设每个排球 x 元，每个实心球 y 元， 则根据题意列二元一次方程组得： 2 3 95 5 7 230 x y x y      ， 故选 B． 3．（2019·河北中考模拟）陈老师打算购买气球装扮学校“六一”儿童节活动会场，气球的种类有笑脸和爱心 两种，两种气球的价格不同，但同一种气球的价格相同，由于会场布置需要，购买时以一束（4 个气球）为 单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为（ ） A．19 B．18 C．16 D．15 【答案】C 【解析】 要求出第三束气球的价格，根据第一、二束气球的价格列出方程组，应用整体思想求值： 设笑脸形的气球 x 元一个，爱心形的气球 y 元一个，由题意，得 3x y 14{x 3y 18     ， 两式相加，得，4x+4y=32，即 2x+2y=16． 故选 C． 4.（2015·湖北中考模拟）某商店经销一种商品，由于进价降低了 5%，售价不变，使得利润率由 m%提高到 （m+6）%，问：m 值为多少？（ ） A．12 B．14 C．16 D．18 【答案】B 【解析】 设原进价为 x，则： x+m%•x=95%•x+95%•x•（m+6）%， ∴1+m%=95%+95%（m+6）%， ∴100+m=95+0．95（m+6）， ∴0．05m=0．7 解得：m=14． 故选 B． 考查题型十一 列二元一次方程解决行程问题 1．（2018·黑龙江中考模拟）小颖家离学校 1200 米，其中有一段为上坡路，另一段为下坡路.她去学校共用 了 16 分钟.假设小颖上坡路的平均速度是 3 千米 / 时，下坡路的平均速度是 5 千米 / 时.若设小颖上坡用了 x 分钟，下坡用了 y 分钟，根据题意可列方程组为 ( ) A． 3x 5y 1200 x y 16      B． 3 5x y 1.260 60 x y 16       C． 3x 5y 1.2 x y 16      D． 3 5x y 120060 60 x y 16       【答案】B 【详解】 小颖上坡用了 x 分钟，下坡用了 y 分钟，根据题意得 3 5x y 1.260 60 x y 16       ， 故选 B． 2．（2019·浙江中考模拟）滴滴快车是一种便捷的出行工具，计价规则如下表： 计费项目 里程费 时长费 远途费 单价 1.8 元/公里 0.3 元/分钟 0.8 元/公里 注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实 际时间计算；远途费的收取方式为：行车里程 7 公里以内（含 7 公里）不收远途费，超过 7 公里的，超出 部分每公里收 0.8 元. 小王与小张各自乘坐滴滴快车，行车里程分别为 6 公里与 8.5 公里，如果下车时两人所付车费相同，那么这 两辆滴滴快车的行车时间相差（ ） A．10 分钟 B．13 分钟 C．15 分钟 D．19 分钟 【答案】D 【详解】 设小王的行车时间为 x 分钟，小张的行车时间为 y 分钟，依题可得： 1.8×6+0.3x=1.8×8.5+0.3y+0.8×（8.5-7）, 10.8+0.3x=16.5+0.3y, 0.3（x-y）=5.7, x-y=19, 故答案为 D. 考查题型十二 列二元一次方程解决和、差、倍、分问题 1.（2018·湖北中考模拟）已知一个两位数，它的十位上的数字 x 比个位上的数字 y 大 1，若颠倒个位数字与 十位数字的位置，得到的新数比原数小 9，求这个两位数所列的方程组正确的是（ ） A．     1 9 x y x y y x        B．   1 10 9 x y x y y x        C． 1 10 10 9 x y x y y x        D． 1 10 10 9 x y x y y x        【答案】D 【解析】 本题考查的是根据实际问题列方程组 根据等量关系：十位上的数字 x 比个位上的数字 y 大1，若颠倒个位数字与十位数字的位置，得到的新数比 原数小9，即可列出方程组。 根据十位上的数字 x 比个位上的数字 y 大1，可列方程为 ， 根据若颠倒个位数字与十位数字的位置，得到的新数比原数小9，可列方程为 ， 则可列方程组为 1{10 10 9 x y x y y x       ， ，故选 D。 2．（2019·浙江中考模拟）一个两位数，十位数字比个位数字的 2 倍大 1，若将这个两位数减去 36 恰好等于 个位数字与十位数字对调后所得的两位数，则这个两位数是（ ） A．86 B．68 C．97 D．73 【答案】D 【详解】 设这个两位数的十位数字为 x，个位数字为 y． 则   2 1 10 36 10 x y x y y x      ＝ ＝ ， 解得 7 3 x y ＝ ＝    ． 故选 D． 3．（2014·辽宁中考真题）为了节省空间，家里的饭碗一般是摞起来存放的．如果 6 只饭碗摞起来的高度为 15cm，9 只饭碗摞起来的高度为 20cm，那么 11 只饭碗摞起来的高度更接近（ ） A．21cm B．22cm C．23cm D．24cm 【答案】C 【详解】 试题分析：设碗的个数为 x 个，碗的高度为 ycm，由题意可知碗的高度和碗的个数的关系式为 y=kx+b， 由题意得， 6 15 9 20 k b k b      ， 解得： 5 3 5 k b     ， 则 11 只饭碗摞起来的高度为： 5 3 ×11+5= 70 1233 3  （cm）． 更接近 23cm． 故选 C． 4．（2017·浙江中考模拟）已知甲、乙两数的和是 7，甲数是乙数的 2 倍．设甲数为 x，乙数为 y，根据题意， 列方程组正确的是（ ） A． 7{ 2 x y x y    B． 7{ 2 x y y x    C． 2 7{ 2 x y x y    D． 2 7{ 2 x y y x    【答案】A 【详解】 设甲数为 x，乙数为 y， 根据题意得： 7{ 2 x y x y    ， 故选 A. 5．（2019·山东中考模拟）甲数的 2 倍比乙数大 3，甲数的 3 倍比乙数的 2 倍小 1，若设甲数为 x，乙数为 y， 则根据题意可列出的方程组为（ ） A． 2 3 3 2 1 x y x y      B． 2 3 3 1 2 x y x y      C． 2 3 3 2 1 x y x y      D． 2 3 3 2 1 x y x y      【答案】C 【解析】 解：设甲数为 x，乙数为 y，根据题意得： 2 3 3 2 1 x y x y      ，故选 C． 考查题型十三 列二元一次方程解决方案问题 1．（2019·黑龙江中考模拟）某校九年级（1）班为了筹备演讲比赛，准备用 200 元钱购买日记本和钢笔两种 奖品（两种都要买），其中日记本 10 元/本，钢笔 l5 元/支，在钱全部用完的条件下，购买的方案共有（ ） A．4 种 B．5 种 C．6 种 D．7 种 【答案】C 【详解】 设购买日记本 x 本，钢笔 y 支， ∴10x+15y=200，即 2x+3y=40， ∵x、y 均为整数， ∴x=2 时，y=12， x=5 时，y=10， x=8 时，y=8， x=11 时，y=6， x=14 时，y=4， x=17 时，y=2， ∴共有 6 种购买方案， 故选 C. 考查题型十四 列二元一次方程解决几何问题 1．（2018·黑龙江中考真题）如图，在长为 15，宽为 12 的矩形中，有形状、大小完全相同的 5 个小矩形， 则图中阴影部分的面积为（ ） A．35 B．45 C．55 D．65 【答案】B 【详解】 解：设小矩形的长为 a，宽为 b，可得方程组： a+2b=15，a=3b， 可得解：a=9，b=3， 故阴影部分的面积：15 12-5 3 9=45， 故选 B. 2．（2015·四川中考真题）一副三角板按如图方式摆放，且∠1 的度数比∠2 的度数大 50°，若设∠1=x°， ∠2=y°，则可得到方程组为（ ） A． x y 50{x y 180     B． x y 50{x y 180     C． x y 50{x y 90     D． x y 50{x y 90     【答案】C 【解析】 根据平角和直角定义，得方程 x+y=90；根据∠1 比∠2 的度数大 50°，得方程 x=y+50．可列方程组为 50{ 90 x y x y     ，故选 D． 3．（2019·河南中考模拟）如图所示，8 块相同的小长方形地砖拼成一个大长方形，若其中每一个小长方形 的长为 x，宽为 y，则依据题意可得二元一次方程组为（ ） A． 15 3 x y x y     B． 15 2 3 x y x y     C． 15 2 3 x y x x y      D． 2 15 2 3 x y x x y      【答案】A 【详解】 解：设每一个小长方形的长为 x，宽为 y， 依题意，得： 15 3 x y x y     ． 故选 A．