2021年中考数学专题复习 专题18 等腰、等边三角形问题（学生版） 8页

专题 18 等腰、等边三角形问题 一、等腰三角形 1. 定义：两边相等的三角形叫做等腰三角形，其中相等的两条边叫腰，第三条边叫底边，两腰的夹角叫顶 角，底边和腰的夹角叫底角. 2.等腰三角形的性质 性质 1：等腰三角形的两个底角相等(简称“等边对等角”)． 性质 2：等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(简称“三线合一”)． 3.等腰三角形的性质的作用 性质 1 证明同一个三角形中的两角相等.是证明角相等的一个重要依据． 性质 2 用来证明线段相等，角相等，垂直关系等． 4.等腰三角形是轴对称图形 等腰三角形底边上的高(顶角平分线或底边上的中线)所在直线是它的对称轴，通常情况只有一条对称轴． 5.等腰三角形的判定 如果一个三角形中有两个角相等，那么这两个角所对的边也相等(简称“等角对等边”). 要点诠释：等腰三角形的判定是证明两条线段相等的重要定理，是将三角形中的角的相等关系转化为边的 相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理. 二、等边三角形 1. 定义：三边都相等的三角形叫等边三角形． 2. 性质 性质 1：等边三角形的三个内角都相等，并且每一个角都等于 60°； 性质 2：等边三角形是轴对称图形，并且有三条对称轴，分别为三边的垂直平分线。 3.判定 (1)三个角都相等的三角形是等边三角形； (2)有一个角是 60°的等腰三角形是等边三角形； (3)有两个角是 60°的三角形是等边三角形。 三、解题方法要领 1.等腰(边)三角形是一个特殊的三角形，具有较多的特殊性质，有时几何图形中不存在 等腰(边)三角形，可根据已知条件和图形特征，适当添加辅助线，使之构成等腰(边)三角形，然后利用其 定义和有关性质，快捷地证出结论。 2.常用的辅助线有：(1)作顶角的平分线、底边上的高线、中线。(2)在三角形的中线问 题上，我们常将中线延长一倍，这样添辅助线有助于我们解决有关中线的问题。 3.分类讨论是等腰三角形问题中常用的思想方法，在已知等腰三角形的边和角的情况下求其他三角形的边 或角，要对已知的边和角进行讨论，分类的标准一般是根据边是腰还是底来分类。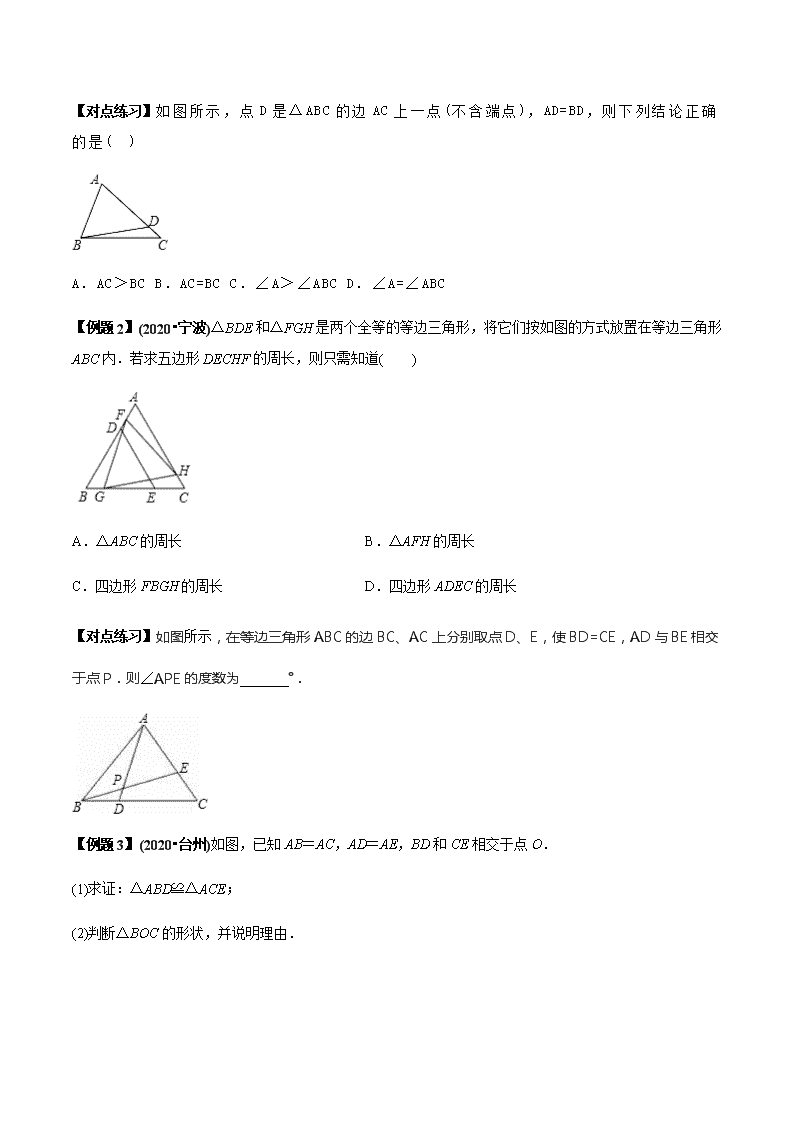 【例题 1】(2020•临沂)如图，在△ABC 中，AB＝AC，∠A＝40°，CD∥AB，则∠BCD＝( ) A．40° B．50° C．60° D．70° 【对点练习】如 图 所 示 ， 点 D 是 △ ABC 的 边 AC 上 一 点 (不 含 端 点 )， AD=BD， 则 下 列 结 论 正 确 的 是 ( ) A． AC＞ BC B． AC=BC C． ∠ A＞ ∠ ABC D． ∠ A=∠ ABC 【例题 2】(2020•宁波)△BDE 和△FGH 是两个全等的等边三角形，将它们按如图的方式放置在等边三角形 ABC 内．若求五边形 DECHF 的周长，则只需知道( ) A．△ABC 的周长 B．△AFH 的周长 C．四边形 FBGH 的周长 D．四边形 ADEC 的周长 【对点练习】如图所示，在等边三角形 ABC 的边 BC、AC 上分别取点 D、E，使 BD=CE，AD 与 BE 相交于 点 P．则∠APE 的度数为 °． 【例题 3】(2020•台州)如图，已知 AB＝AC，AD＝AE，BD 和 CE 相交于点 O． (1)求证：△ABD≌△ACE； (2)判断△BOC 的形状，并说明理由． 【对点练习】如图，已知 AC⊥BC，BD⊥AD，AC 与 BD 交于点 O，AC=BD.求证： (1)BC=AD； (2)△OAB 是等腰三角形. 【对点练习】已知：在△ABC 中，AB=AC，D 为 AC 的中点，DE⊥AB，DF⊥BC，垂足分别为点 E，F， 且 DE=DF．求证：△ABC 是等边三角形． 【对点练习】如图，△ABC 中，AB=AC，∠A=36°，AC 的垂直平分线交 AB 于 E，D 为垂足，连接 EC． (1)求∠ECD 的度数；(2)若 CE=5，求 BC 长． 一、选择题 1．(2020•聊城)如图，在△ABC 中，AB＝AC，∠C＝65°，点 D 是 BC 边上任意一点，过点 D 作 DF∥AB 交 AC 于点 E，则∠FEC 的度数是( ) A．120° B．130° C．145° D．150° 2．(2020•南充)如图，在等腰△ABC 中，BD 为∠ABC 的平分线，∠A＝36°，AB＝AC＝a，BC＝b，则 CD ＝( ) A． Ro B． 㐠o C．a﹣b D．b﹣a 3．(2020•徐州)如图，AB 是 ⊙ O 的弦，点 C 在过点 B 的切线上，OC⊥OA，OC 交 AB 于点 P．若∠BPC＝ 70°，则∠ABC 的度数等于( ) A．75° B．70° C．65° D．60° 4.已 知 等 边 三 角 形 的 边 长 为 3，点 P 为 等 边 三 角 形 内 任 意 一 点 ，则 点 P 到 三 边 的 距 离 之 和 为 ( ) A． B． C． D． 不 能 确 定 5.(2019•浙江衢州)“三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能 三等分任一角。这个三等分角仪由两根有槽的棒 OA，OB 组成，两根棒在 O 点相连并可绕 O 转动，C 点固 定，OC=CD=DE，点 D，E 可在槽中滑动，若∠BDE=75°，则∠CDE 的度数是( ) A. 60° B. 65° C. 75° D. 80° 6.(2019•湖南长沙)如图，Rt△ABC 中，∠C＝90°，∠B＝30°，分别以点 A 和点 B 为圆心，大于 AB 的长 为半径作弧，两弧相交于 M、N 两点，作直线 MN，交 BC 于点 D，连接 AD，则∠CAD 的度数是( ) A．20°B．30°C．45° D．60° 二、填空题 7．(2020•台州)如图，等边三角形纸片 ABC 的边长为 6，E，F 是边 BC 上的三等分点．分别过点 E，F 沿着 平行于 BA，CA 方向各剪一刀，则剪下的△DEF 的周长是 ． 8．(2020•牡丹江)如图，在 Rt△ABC 中，CA＝CB，M 是 AB 的中点，点 D 在 BM 上，AE⊥CD，BF⊥CD， 垂足分别为 E，F，连接 EM．则下列结论中： ① BF＝CE； ② ∠AEM＝∠DEM； ③ AE﹣CE ME； ④ DE2+DF2＝2DM2； ⑤ 若 AE 平分∠BAC，则 EF：BF ：1； ⑥ CF•DM＝BM•DE， 正确的有 ．(只填序号) 9．如图所示，D 是等边△ABC 的 AC 边上的中点，点 E 在 BC 的延长线上，DE=DB，△ABC 的周长是 9，则 ∠E= °，CE= ． 10.(2019 黑龙江绥化)如图,在△ABC 中,AB＝AC,点 D 在 AC 上,且 BD＝BC＝AD,则∠A＝______度. 三、解答题 11．(2020•绍兴)问题：如图，在△ABD 中，BA＝BD．在 BD 的延长线上取点 E，C，作△AEC，使 EA＝EC．若 ∠BAE＝90°，∠B＝45°，求∠DAC 的度数． 答案：∠DAC＝45°． 思考：(1)如果把以上“问题”中的条件“∠B＝45°”去掉，其余条件不变，那么∠DAC 的度数会改变吗？ 说明理由． (2)如果把以上“问题”中的条件“∠B＝45°”去掉，再将“∠BAE＝90°”改为“∠BAE＝n°”，其余条 件不变，求∠DAC 的度数． 12．(2020•凉山州)如图，点 P、Q 分别是等边△ABC 边 AB、BC 上的动点(端点除外)，点 P、点 Q 以相同的 速度，同时从点 A、点 B 出发． (1)如图 1，连接 AQ、CP．求证：△ABQ≌△CAP； (2)如图 1，当点 P、Q 分别在 AB、BC 边上运动时，AQ、CP 相交于点 M，∠QMC 的大小是否变化？若变 化，请说明理由；若不变，求出它的度数； (3)如图 2，当点 P、Q 在 AB、BC 的延长线上运动时，直线 AQ、CP 相交于 M，∠QMC 的大小是否变化？ 若变化，请说明理由；若不变，求出它的度数．