苏教版数学九年级上册课件2-1圆（2） 17页

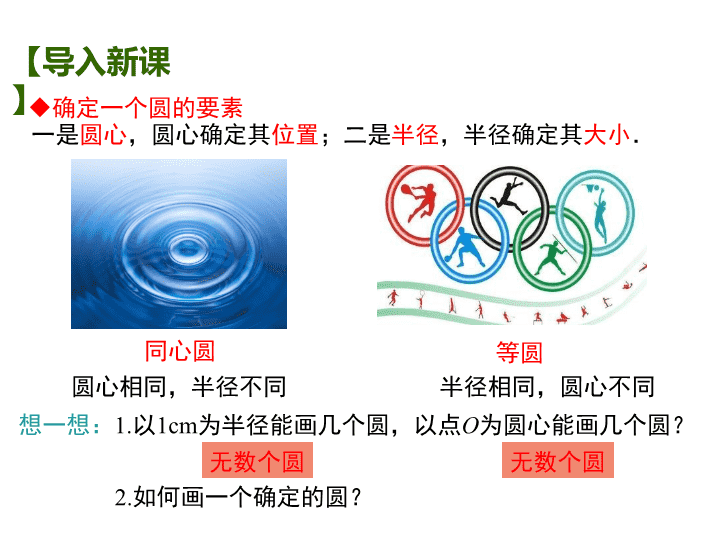
2.1 圆（2） 一是圆心，圆心确定其位置；二是半径，半径确定其大小． 同心圆 等圆 半径相同，圆心不同圆心相同，半径不同 想一想：1.以1cm为半径能画几个圆，以点O为圆心能画几个圆？ 无数个圆 无数个圆 u确定一个圆的要素 2.如何画一个确定的圆？ 【导入新课】 u弦: · CO A B 连接圆上任意两点的线段（如图中的AC）叫 做弦. 经过圆心的弦（如图中的AB）叫做直径． 1.弦和直径都是线段. 2.直径是弦,是经过圆心的特殊弦，是圆中最长的弦，但弦 不一定是直径. 注意 u弧: · C O A B 圆的任意一条直径的两个端点把圆分成 两条弧，每一条弧都叫做半圆． Ø劣弧与优弧 · C O A B Ø半圆 圆上任意两点间的部分叫做圆弧，简弧． 以A、B为端点的弧记作 AB ，读作“圆弧 AB”或“弧AB”． ( 小于半圆的弧叫做劣弧.如图中的AC ; ( 大于半圆的弧叫做优弧.如图中的ABC. ( u等圆: · CO A 能够重合的两个圆叫做等圆. · CO1 A 容易看出： 等圆是两个半径相等的圆. u等弧: 在同圆或等圆中，能够互相重合的弧 叫做等弧. 想一想：长度相等的弧就是等弧？ 观察AD和BC是否 相等？ u圆心角: 顶点在圆心，并且两边都和圆周相交的角叫做圆心角.　 · C O A B ∠AOC　 ∠BOC 找出下图中的圆心角． 想一想：∠ABC 是不是圆心角？ 例1 如图. (1)请写出以点A为端点的优弧及劣弧; (2)请写出以点A为端点的弦及直径. 典例精析 弦AF,AB,AC.其中弦AB又是直径. （3）请任选一条弦，写出这条弦所对的弧. 答案不唯一，如：弦AF,它所对的弧是 . A B C EF D O 劣弧： 优弧： AF， ( AD, ( AC, ( AE. ( AFE, ( AFC, ( ADE, ( ADC. ( AF ( 同圆中半径相等的性质的应用 问题 车轮为什么做成圆形? 　把车轮做成圆形，车轮上各点到车轮中心（圆 心）的距离都等于车轮的半径，当车轮在平面上滚动时， 车轮中心与平面的距离保持不变，因此，当车辆在平坦 的路上行驶时，坐车的人会感觉到非常平稳，这也是车 轮都做成圆形的数学道理． 圆的基本性质 o• 同圆半径相等. （1）圆上各点到定点（圆心O） 的距离都等于 ． （2）到定点的距离等于定长的 点都在 ． 定长r 同一个圆上 圆心为O、半径为r的圆可以看成是所有 到定点O的距离等于定长r的点的集合． u圆的集合定义 r r r r r r r 例2 矩形ABCD的对角线AC、BD相交于O. 求证：A、B、C、D在以O为圆心的同一圆上. A B C D O 证明：∵四边形ABCD是矩形， ∴AO=OC，OB=OD. 又∵AC=BD， ∴OA=OB=OC=OD. ∴A、B、C、D在以O为圆心以OA为半径的圆上. 1.填空： （1）______是圆中最长的弦，它是______的2倍． （2）图中有 条直径， 条非直径的弦， 圆中以A为一个端点的优弧有 条， 劣弧有 条． 直径 半径 一 二 四 四 2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm, 则这个圆的半径是 .7cm或3cm A B C D O F E 【练习】 3.判断下列说法的正误，并说明理由或举反例. (1)弦是直径； (2)半圆是弧； (3)过圆心的线段是直径； (4)过圆心的直线是直径； (5)半圆是最长的弧； (6)直径是最长的弦； (7)长度相等的弧是等弧. 4． 一些学生正在做投圈游戏，他们呈“一”字排开． 这样的队形对每一人都公平吗？你认为他们应当排成什 么样的队形？ 不公平，应该站成圆形. 5． 一根5m长的绳子，一端栓在柱子上，另一端栓着一只 羊，请画出羊的活动区域． 5m 5 m O 4 m 4 参考答案： 圆 定 义 旋 转 定 义 要画一个确定的 圆 ， 关 键 是 确定圆心和半径 集 合 定 义 同圆半径相等 有关 概念 弦（直径） 直径是圆中 最 长 的 弦 弧 半圆是特殊的弧 劣 弧 半 圆 优 弧 同心圆 等圆同圆 等弧 能够互相重合的两段弧 圆心角 顶点在圆心，并且两 边都和圆周相交的角　 【小结】