苏科版九年级第一学期数学期中试题（苏教版九年级数学上册期中考试测试卷） 4页

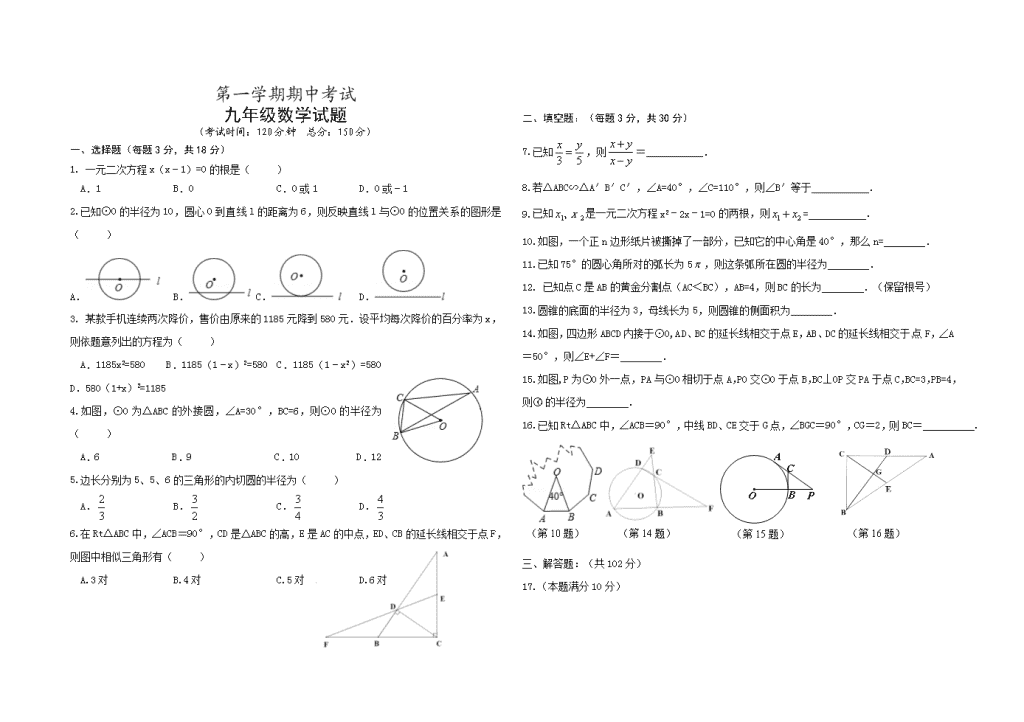
第一学期期中考试 九年级数学试题 （考试时间：120 分钟 总分：150 分） 一、选择题（每题 3 分，共 18 分） 1. 一元二次方程 x（x﹣1）=0 的根是（ ） A．1 B．0 C．0 或 1 D．0 或﹣1 2.已知⊙O 的半径为 10，圆心 O 到直线 l 的距离为 6，则反映直线 l 与⊙O 的位置关系的图形是 （ ） A． B． C． D． 3. 某款手机连续两次降价，售价由原来的 1185 元降到 580 元．设平均每次降价的百分率为 x， 则依题意列出的方程为（ ） A．1185x2=580 B．1185（1﹣x）2=580 C．1185（1﹣x2）=580 D．580（1+x）2=1185 4.如图，⊙O 为△ABC 的外接圆，∠A=30°，BC=6，则⊙O 的半径为 （ ） A．6 B．9 C．10 D．12 5.边长分别为 5、5、6 的三角形的内切圆的半径为（ ） A． 3 2 B． 2 3 C． 4 3 D． 3 4 6.在 Rt△ABC 中，∠ACB＝90°，CD 是△ABC 的高，E 是 AC 的中点，ED、CB 的延长线相交于点 F， 则图中相似三角形有（ ） A.3 对 B.4 对 C.5 对 D.6 对 二、填空题：（每题 3 分，共 30 分） 7.已知 53 yx  ，则 yx yx   ＝ ． 8.若△ABC∽△A′B′C′，∠A=40°，∠C=110°，则∠B′等于 ． 9.已知 21、xx 是一元二次方程 x2﹣2x﹣1=0 的两根，则 21 xx  = ． 10.如图，一个正 n 边形纸片被撕掉了一部分，已知它的中心角是 40°，那么 n= ． 11.已知 75°的圆心角所对的弧长为 5 ，则这条弧所在圆的半径为 ． 12. 已知点 C 是 AB 的黄金分割点（AC＜BC），AB=4，则 BC 的长为 ．（保留根号） 13.圆锥的底面的半径为 3，母线长为 5，则圆锥的侧面积为 ． 14.如图，四边形 ABCD 内接于⊙O,AD、BC 的延长线相交于点 E，AB、DC 的延长线相交于点 F，∠ A＝50°，则∠E+∠F＝ ． 15.如图,P 为⊙O 外一点，PA 与⊙O 相切于点 A，PO 交⊙O 于点 B，BC⊥OP 交 PA 于点 C，BC=3， PB=4，则⊙O 的半径为 ． 16.已知 Rt△ABC 中，∠ACB＝90°，中线 BD、CE 交于 G 点，∠BGC＝90°，CG＝2，则 BC＝ . 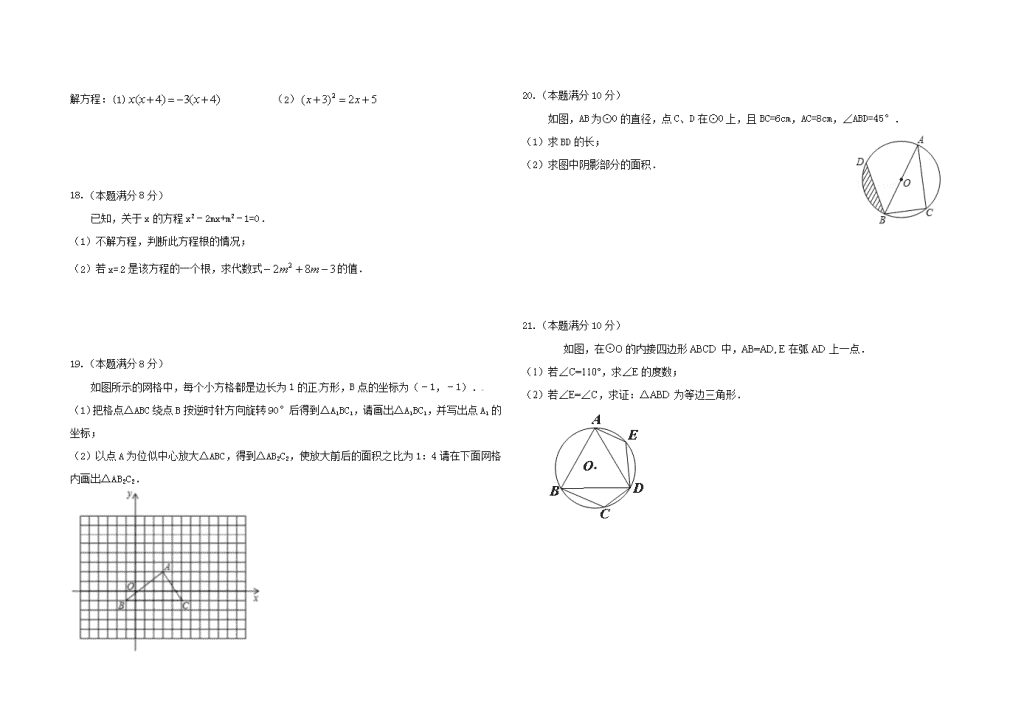三、解答题：（共 102 分） 17.（本题满分 10 分） （第 10 题） （第 14 题） （第 15 题） （第 16 题） 解方程：(1) )4(3)4(  xxx （2） 52)3( 2  xx 18.（本题满分 8 分） 已知，关于 x 的方程 x2﹣2mx+m2﹣1=0． （1）不解方程，判断此方程根的情况； （2）若 x=2 是该方程的一个根，求代数式 382 2  mm 的值． 19.（本题满分 8 分） 如图所示的网格中，每个小方格都是边长为 1 的正方形，B 点的坐标为（﹣1，﹣1）． （1）把格点△ABC 绕点 B 按逆时针方向旋转 90°后得到△A1BC1，请画出△A1BC1，并写出点 A1 的 坐标； （2）以点 A 为位似中心放大△ABC，得到△AB2C2，使放大前后的面积之比为 1：4 请在下面网格 内画出△AB2C2． 20.（本题满分 10 分）x k b 1 . 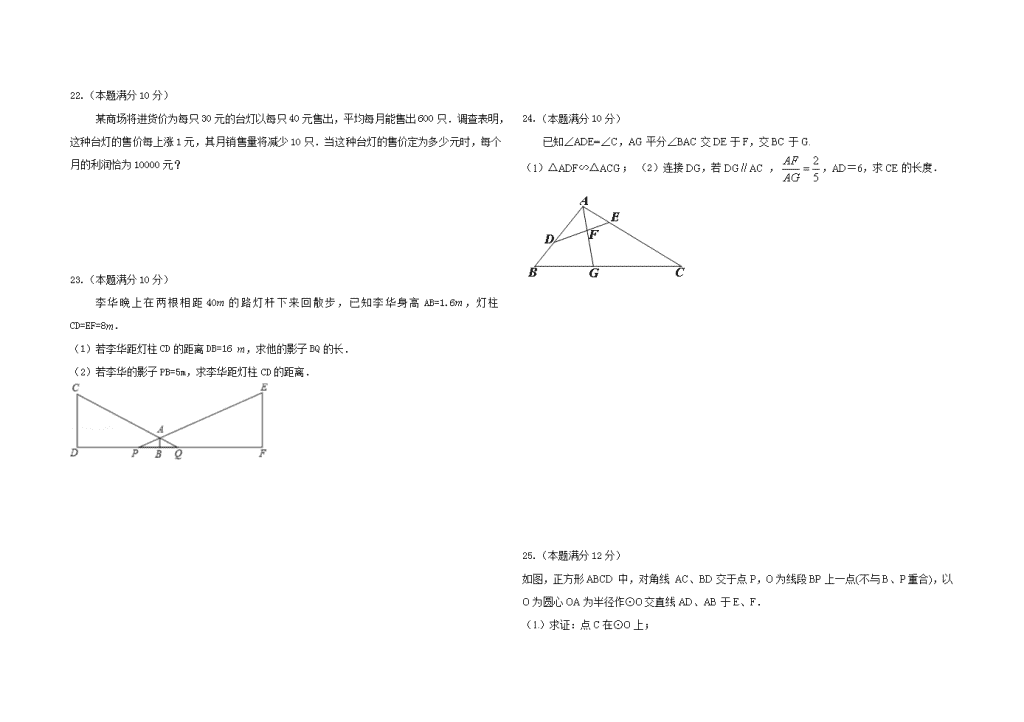c o m 如图，AB 为⊙O 的直径，点 C、D 在⊙O 上，且 BC=6cm，AC=8cm，∠ABD=45°． （1）求 BD 的长； （2）求图中阴影部分的面积． 21.（本题满分 10 分） 如图，在⊙O 的内接四边形 ABCD 中，AB=AD,E 在弧 AD 上一点． （1）若∠C=110°，求∠E 的度数； （2）若∠E=∠C，求证：△ABD 为等边三角形． 22.（本题满分 10 分） 某商场将进货价为每只 30 元的台灯以每只 40 元售出，平均每月能售出 600 只．调查表明， 这种台灯的售价每上涨 1 元，其月销售量将减少 10 只．当这种台灯的售价定为多少元时，每个 月的利润恰为 10000 元？ 23.（本题满分 10 分） 李华晚上在两根相距 40m 的路灯杆下来回散步，已知李华身高 AB=1.6m，灯柱 CD=EF=8m． （1）若李华距灯柱 CD 的距离 DB=16 m，求他的影子 BQ 的长． （2）若李华的影子 PB=5m，求李华距灯柱 CD 的距离． 24.（本题满分 10 分） 已知∠ADE=∠C，AG 平分∠BAC 交 DE 于 F，交 BC 于 G. （1）△ADF∽△ACG； （2）连接 DG，若 DG∥AC ， 5 2 AG AF ，AD＝6，求 CE 的长度． 25.（本题满分 12 分） 如图，正方形 ABCD 中，对角线 AC、BD 交于点 P，O 为线段 BP 上一点(不与 B、P 重合)，以 O 为圆心 OA 为半径作⊙O 交直线 AD、AB 于 E、F． （1）求证：点 C 在⊙O 上； （2）求证：DE＝BF； （3）若 AB＝ 24 ，DE＝ 2 ，求 BO 的长度． 26.（本题满分 14 分） 已知，在平面直角坐标系中，A 点坐标为（0，m）( 0m )，B 点坐标为（2，0），以 A 点为圆心 OA 为半径作⊙A，将△AOB 绕 B 点顺时针旋转 角（0°< <360°）至△A/O/B 处． （1）如图 1， 4m , ＝90°，求 O/点的坐标及 AB 扫过的面积； （2）如图 2，当旋转到 A、O/、A/三点在同一直线上时，求证：O/B 是⊙O 的切线； （3）如图 3， 2m ,在旋转过程中，当直线 BO/与⊙A 相交时，直接写出 的范围． 图 1 图 2 图 3 备用图