中考数学一轮复习知识点+题型专题讲义08 整式的乘除与因式分解（学生版） 10页

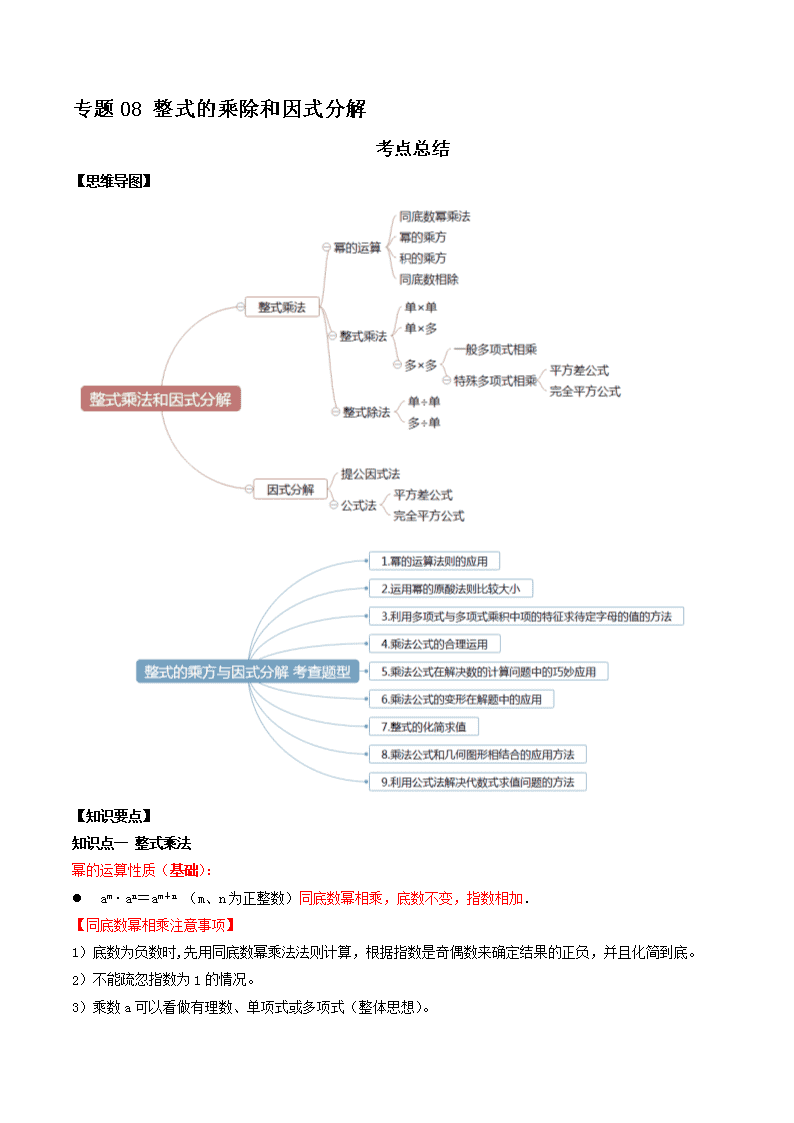
专题 08 整式的乘除和因式分解 考点总结 【思维导图】 【知识要点】 知识点一 整式乘法 幂的运算性质（基础）：  am·an＝am＋n （m、n 为正整数）同底数幂相乘，底数不变，指数相加． 【同底数幂相乘注意事项】 1）底数为负数时,先用同底数幂乘法法则计算，根据指数是奇偶数来确定结果的正负，并且化简到底。 2）不能疏忽指数为 1 的情况。 3）乘数 a 可以看做有理数、单项式或多项式（整体思想）。 4）如果底数互为相反数时可先变成同底后再运算。 1．（2018·河北中考真题）若 2n+2n+2n+2n=2，则 n=（ ） A．﹣1 B．﹣2 C．0 D． 1 4 2．（2012·江苏中考真题）若 3 9m 27m= ，则 的值是（ ） A．3 B．4 C．5 D．6 3．（2019·山东中考模拟）化简(﹣a2)•a5 所得的结果是( ) A．a7 B．﹣a7 C．a10 D．﹣a10  (am)n＝amn （m、n 为正整数）幂的乘方，底数不变，指数相乘． 【同底数幂相乘注意事项】负号在括号内时,偶次方结果为正,奇次方为负,负号在括号外结果都为负。 1．（2019·浙江省温岭市第四中学中考模拟）下列计算正确的是（ ） A．a2•a3＝a6 B．（a2）3＝a6 C．a6﹣a2＝a4 D．a5+a5＝a10 2．（2019·辽宁中考模拟）下列运算正确的是（ ） A．a2•a2=2a2 B．a2+a2=a4 C．（a3）2=a6 D．a8÷a2=a4 3．（2018·浙江中考模拟）计算（﹣a3）2 的结果是（ ） A．a5 B．﹣a5 C．a6 D．﹣a6  (ab)n＝anbn （n 为正整数） 积的乘方等于各因式乘方的积． 1．（2018·湖南中考真题）下列运算正确的是（ ） A． 3 3 9·x x x B． 8 4 2x x x  C． 23 6ab ab D． 3 32 8x x 2．（2018·贵州中考真题）下列运算正确的是（ ） A．（﹣a2）3=﹣a5 B．a3•a5=a15 C．（﹣a2b3）2=a4b6 D．3a2﹣2a2=1  am ÷an＝am－n （a≠0，m、n 都是正整数，且 m＞n） 同底数幂相除，底数不变，指数减． 【同底数幂相除注意事项】 1.因为 0 不能做除数，所以底数 a≠0. 2.运用同底数幂法则关键看底数是否相同，而指数相减是指被除式的指数减去除式的指数。 3.注意指数为 1 的情况，如 x8÷x= x7 ，计算时候容易遗漏或将 x 的指数当做 0. 4.多个同底数幂相除时，应按顺序计算。  a0＝1 （a≠0）任何一个不等于零的数的零指数幂都等于 l． 1．（2016·江苏中考真题）下列计算正确的是（ ） A． B． C． D． 2.．（2018·丹东市第十八中学中考模拟）下列计算正确的是( ). A． 2 2 4x x x+ = B． 8 2 4x x x  C． 2 3 6x x x  D． 2 2( ) 0x x   3．（2016·福建中考模拟）下列运算正确的是( ) A．2a2+a=3a3 B．(m2)3=m5 C．(x+y)2=x2+y2 D．a6÷a3=a3 考查题型一 幂的运算法则的应用 1．（2019·浙江杭州外国语学校中考模拟）若 2m＝5，4n＝3，则 43n﹣m 的值是( ) A． 9 10 B． 27 25 C．2 D．4 2．（2019·海口市长流中学中考模拟）已知 x+y﹣4=0，则 2y•2x 的值是( ) A．16 B．﹣16 C． 1 8 D．8 3．（2012·山东中考真题）若 4, 9 7 ，则 y 的值为（ ） A． 4 7 B． 7 4 C． D． 7 4．（2018·江苏中考模拟）若 3 9 15( )m na b a b ，则 ,m n 的值分别为( ) A．9，5 B．3，5 C．5，3 D．6，12 5．（2018·湖南中考模拟）已知 am=2，an=3，则 a3m+2n 的值是（ ） A．24 B．36 C．72 D．6 考查题型二 运用幂的原酸法则比较大小 1．（2019·杭州市余杭区乾元中学中考模拟）若 9 99 99 9a  ， 9 90 11 9b  ，则下列结论正确是（ ） A．a＜b B． a b C．a＞b D． 1ab  2．（2017·湖北中考模拟）已知 31 41 6181 27 9a b c  ， ， ，则 a b c、 、 的大小关系是（ ） A． a b c＞ ＞ B． a c b＞ ＞ C． a b c＜ ＜ D．b c a＞ ＞ 知识点二 整式乘除  单项式×单项式 单项式的乘法法则：单项式相乘，把系数、同底数幂分别相乘，作为积的因式；对于只在一个单项式里含 有的字母，则连同它的指数作为积的一个因式． 单项式乘法易错点： 【注意】 1. 单项式乘以单项式的结果仍是单项式。 2. 运算顺序：先算乘方，再算乘法。 1．（2017·安徽中考模拟） 2( ) ( )m m ma a 不等于（ ） A． 2( )m ma  B． 2( )m ma a C． 2 2m ma  D． 3 1( ) ( )m m ma a  2．（2018·山东中考模拟）计算：（−x）3·2x 的结果是 A．−2x4 B．−2x3 C．2x4 D．2x3 3．（2018·湖南中考模拟）如果单项式－3x4a－by2 与 x3ya＋b 的和是单项式，那么这两个单项式的积是（ ） A．3x6y4 B．－3x3y2 C．－3x3y2 D．－3x6y4  单项式×多项式 单项式与多项式相乘，用单项式和多项式的每一项分别相乘，再把所得的积相加 【单项式乘以多项式注意事项】 1.单项式乘多项式的结果是多项式，积的项数与原多项式的项数相同。 2.单项式分别与多项式的每一项相乘时，要注意积的各项符号。（同号相乘得正，异号相乘得负） 3.不要出现漏乘现象，运算要有顺序。 1.（2018·湖北中考真题）计算（a﹣2）（a+3）的结果是（ ） A．a2﹣6 B．a2+a﹣6 C．a2+6 D．a2﹣a+6 2．（2019·山东中考真题）计算 2 2 3( 2 ) ( 3 )m m m m     的结果是（ ） A．8m5 B．-8m5 C．8m6 D．-4m4+12m5 3．（2019·广西中考真题）计算： 2( 1)x x   （ ） A． 3 1x  B． 3x x C． 3x x D． 2x x  多项式×多项式 多项式与多项式相乘，先用一个多项式的每一项与另一个多项式的每一项相乘，再把所得的积相加． 【多项式乘以多项式注意事项】 多项式与多项式相乘时，多项式的每一项都应该带上它前面的正负号。多项式是单项式的和，每一项都包 括前面的符号，在计算时一定要注意确定各项的符号。 1．（2018·内蒙古中考模拟）计算 ( 1)( 2)x x  的结果为( ) A． 2 2x  B． 2 3 2x x  C． 2 3 3x x  D． 2 2 2x x  2．（2018·湖北中考模拟）计算（x－2）（x+5）的结果是（ ） A．x2+3x+7 B．x2+3x+10 C．x2+3x－10 D．x2－3x－10 3．（2015·广东中考真题）若（x+2）（x﹣1）=x2+mx+n，则 m+n=（ ） A．1 B．-2 C．-1 D．2  乘法公式 1 完全平方公式：（a＋b）2＝a2＋2ab＋b2 （a－b）2＝a2－2ab＋b2 【扩展】 扩展一(公式变化)： + -2ab + +2ab 扩展二： + = 2( + ) - = 4ab 扩展三： + + = -2ab-2ac-2bc ② 平方差公式：（a＋b）（a－b）＝a2－b2 【运用平方差公式注意事项】 1.对因式中各项的系数、符号要仔细观察、比较，不能误用公式．如：(a＋3b)(3a-b)，不能运用平方差公 式． 2.公式中的字母 a、b 可以是一个数、一个单项式、一个多项式。所以，当这个字母表示一个负数、分式、 多项式时，应加括号避免出现只把字母平方，而系数忘了平方的错误． 1．（2018·河北中考真题）将 9.52 变形正确的是（ ） A．9.52=92+0.52 B．9.52=（10+0.5）（10﹣0.5） C．9.52=102﹣2×10×0.5+0.52 D．9.52=92+9×0.5+0.52 2．（2018·四川中考模拟）已知 x2+mx+25 是完全平方式，则 m 的值为（ ） A．10 B．±10 C．20 D．±20 3．（2018·甘肃中考模拟）已知一个圆的半径为 Rcm，若这个圆的半径增加 2cm，则它的面积增加（ ） A．4πcm2 B．（2πR+4π）cm2 C．（4πR+4π）cm2 D．以上都不对 4．（2019·上海中考模拟）下列各式的变形中，正确的是( ) A．(－x－y)(－x＋y)＝x2－y2 B． －x＝ C．x2－4x＋3＝(x－2)2＋1 D．x÷(x2＋x)＝ ＋1  单项式÷单项式 一般地,单项式相除,把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它 的指数作为商的一个因式. 【同底数幂相除注意事项】 1.因为 0 不能做除数，所以底数 a≠0. 2.运用同底数幂法则关键看底数是否相同，而指数相减是指被除式的指数减去除式的指数。 3.注意指数为 1 的情况，计算时候容易遗漏或将 x 的指数当做 0. 4.多个同底数幂相除时，应按顺序计算。 1．（2018·陕西中考模拟）下列各式中，计算正确的是（ ） A．2x+3y=5xy B．x6÷x2=x3 C．（﹣2x3y）3=﹣8x9y3 D．x2y•x3y=x5y 2．（2018·湖南中考真题）下列运算正确的是( ) A． 2 3 5a b ab  B． 2 2( )ab a b  C． 2 4 8a a a  D． 6 3 3 2 2a aa  3.（2019·江苏中考真题）如图，数轴上有O 、 A 、 B 三点，O 为O 原点，OA、OB 分别表示仙女座星系、 M87 黑洞与地球的距离（单位：光年）．下列选项中，与点 B 表示的数最为接近的是（ ） A． 65 10 B． 710 C． 75 10 D． 810  多项式÷单项式 一般地，多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加. 【解题思路】 多项式除以单项式问题转化为单项式除以单项式问题解决。 1．（2019·河南中考模拟）下列运算结果正确的是（ ） A．（x3﹣x2+x）÷x=x2﹣x B．（﹣a2）•a3=a6 C．（﹣2x2）3=﹣8x6 D．4a2﹣（2a）2=2a2 2．（2017·海南中考模拟）已知长方形的面积为 18x3y4＋9xy2－27x2y2，长为 9xy，则宽为( ) A．2x2y3＋y＋3xy B．2x2y2－2y＋3xy C．2x2y3＋2y－3xy D．2x2y3＋y－3xy 3．（2015·福建中考真题） 下列运算正确的是（ ） A． B． 4 C． D．  整式的混合运算 运算顺序：先乘方，再乘除，后加减，有括号时先算括号里面的。 1．（2017·安徽中考模拟）设 M=(x﹣3)(x﹣7)，N=(x﹣2)(x﹣8)，则 M 与 N 的关系为( ) A．M＜N B．M＞N C．M=N D．不能确定 2．（2018·广西中考模拟）点 A（a，3）与点 B（4，b）关于 y 轴对称，则（a+b）2017 的值为（ ） A．0 B．﹣1 C．1 D．72017 3．（2018·江苏中考真题）计算：（1）（﹣2）2×|﹣3|﹣（ 6 ）0；（2）（x+1）2﹣（x2﹣x） 考查题型三 利用多项式与多项式乘积中项的特征求待定字母的值的方法 1．（2018·山东中考模拟）若（x﹣2）（x2+ax+b）的积中不含 x 的二次项和一次项，求（2a+b+1）（2a﹣b﹣1） ﹣（a+2b）（﹣2b+a）+2b 的值． 考查题型四 乘法公式的合理运用 1．（2019·乌鲁木齐市第七十七中学中考模拟）计算： （1）（a+2b﹣c）（a﹣2b+c） （2）已知 6x﹣5y＝10，求[（﹣2x+y）（﹣2x﹣y）﹣（2x﹣3y）2]÷4y 的值． 考查题型五 乘法公式在解决数的计算问题中的巧妙应用。 1．（2018·浙江中考模拟）计算：（﹣2018）2+2017×（﹣2019）． 考查题型六 乘法公式的变形在解题中的应用 1．（2019·甘肃中考模拟）已知 x+ 1 x =6，则 x2+ 2 1 x =（ ） A．38 B．36 C．34 D．32 2．（2018·四川中考真题）已知实数 a、b 满足 a+b=2，ab= 3 4 ，则 a﹣b=（ ） A．1 B．﹣ 5 2 C．±1 D．± 5 2 3．（2017·江苏中考模拟）若(x+y)2=9，(x-y)2=5，则 xy 的值为（ ） A．-1 B．1 C．-4 D．4 4．（2019·浙江中考模拟）已知（m-n）2=8，（m+n）2=2，则 m2+n2=（ ） A．10 B．6 C．5 D．3 5．（2015·湖南中考真题）已知 a+b=3，ab=2，则 a2+b2 的值为（ ） A．3 B．4 C．5 D．6 考查题型七 整式的化简求值 1．（2019·辽宁中考模拟）先化简，再求值：（x﹣2y）2+（x+y）（x﹣4y），其中 x＝5，y＝ 1 5 ． 2．（2017·江苏中考模拟）先化简，再求值：2 2b ＋( a ＋b )( a －2b )－( a － 2)b ，其中 a ＝－3， b ＝ 1 2 . 考查题型八 乘法公式和几何图形相结合的应用方法 1．（2019·浙江中考模拟）如图，将边长为 m 的正方形纸板沿虚线剪成两个小正方形和两个矩形，拿掉边 长为 n 的小正方形纸板后，将剩下的三块拼成新的矩形． （1）用含 m 或 n 的代数式表示拼成矩形的周长； （2）m=7，n=4，求拼成矩形的面积． 2．（2018·浙江中考真题）有一张边长为 a 厘米的正方形桌面，因为实际需要，需将正方形边长增加 b 厘米， 木工师傅设计了如图所示的三种方案： 小明发现这三种方案都能验证公式：a2+2ab+b2=（a+b）2，对于方案一，小明是这样验证的： a2+ab+ab+b2=a2+2ab+b2=（a+b）2 请你根据方案二、方案三，写出公式的验证过程． 方案二： 方案三： 知识点四 因式分解（难点） 因式分解的定义：把一个多项式化成几个整式的乘积的形式，这种变形叫做把这个多项式因式分解． 【因式分解的定义注意事项】 1.分解对象是多项式，分解结果必须是积的形式，且积的因式必须是整式，这三个要素缺一不可； 2.因式分解必须是恒等变形； 3.因式分解必须分解到每个因式都不能分解为止． 因式分解与整式乘法是互逆变形，因式分解是把和差化为积的形式，而整式乘法是把积化为和差的形式． 因式分解的常用方法： 提公因式法 【提公因式法的注意事项】 1）定系数：公因式的系数是多项式各项系数的最大公约数。 2）定字母：字母取多项式各项中都含有的相同的字母。 3）定指数：相同字母的指数取各项中最小的一个，即字母最低次幂。 4）查结果：最后检查核实，应保证含有多项式的因式中再无公因式。 公式法 运用公式法分解因式的实质是把整式中的乘法公式反过来使用； ①平方差公式： a2－b2＝（a＋b）（a－b） 2 完全平方公式：a2＋2ab＋b2＝（a＋b）2 a2－2ab＋b2＝（a－b）2 1．（2019·安徽中考模拟）下列分解因式正确的是（ ） A． 2 4 ( 4)x x x x     B． 2 ( )x xy x x x y    C． 2( ) ( ) ( )x x y y y x x y     D． 2 4 4 ( 2)( 2)x x x x     2．（2018·江苏中考模拟）把多项式 x2+ax+b 分解因式，得(x+1)(x-3)，则 a、b 的值分别是（ ） A．a=2，b=3 B．a=-2，b=-3 C．a=-2，b=3 D．a=2，b=-3 3．（2018·广西中考真题）下列各式分解因式正确的是（ ） A．x2+6xy+9y2=（x+3y）2 B．2x2﹣4xy+9y2=（2x﹣3y）2 C．2x2﹣8y2=2（x+4y）（x﹣4y） D．x（x﹣y）+y（y﹣x）=（x﹣y）（x+y） 4．（2019·山东中考模拟）多项式 4a﹣a3 分解因式的结果是（ ） A．a（4﹣a2） B．a（2﹣a）（2+a） C．a（a﹣2）（a+2） D．a（2﹣a）2 5．（2018·安徽中考模拟）将下列多项式因式分解,结果中不含有因式(a+1)的是( ) A．a2-1 B．a2+a C．a2+a-2 D．(a+2)2-2(a+2)+1 考查题型九 利用公式法解决代数式求值问题的方法 1．（2018·河南中考模拟）已知 a﹣b=1，则 a3﹣a2b+b2﹣2ab 的值为（ ） A．﹣2 B．﹣1 C．1 D．2 2．（2017·陕西中考模拟）已知实数 x 满足 2 2 1 1 0x xx x     ，那么 1x x  的值是（ ） A．1 或﹣2 B．﹣1 或 2 C．1 D．﹣2 3．（2019·江苏中考模拟）若 x2+mx-15=(x+3)(x+n)，则 m 的值为( ) A．-5 B．5 C．-2 D．2