人教版九年级上册数学同步课件-第22章-二次函数复习课件 29页

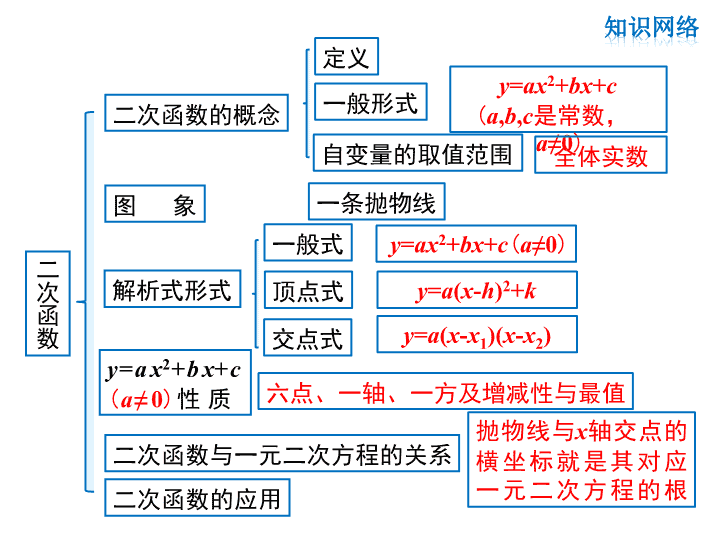
第二十二章 二次函数 复习课 二 次 函 数 二次函数的概念 定义 一般形式 y=ax2+bx+c (a,b,c是常数，a≠0) 自变量的取值范围 全体实数 图 象 一条抛物线 解析式形式 一般式 y=ax2+bx+c(a≠0) 顶点式 y=a(x-h)2+k 交点式 y=a(x-x1)(x-x2) y=ax2+bx+c ( a ≠ 0 )性质 六点、一轴、一方及增减性与最值 二次函数与一元二次方程的关系 抛物线与x轴交点的 横坐标就是其对应 一元二次方程的根二次函数的应用 解析: （1）根据定义可知m2+5m+8=2且m+2≠0; (2)在（1）的基础上根据a的符号再作确定； （3）判断抛物线的增减性要结合开口方向及对称轴. 已知函数 是关于x的二次数. (1) 求满足条件的m的值，并写出解析式； （2）抛物线有最高点和最低点吗？二次函数有最大值还是最 小值？最值是多少？ （3）当x为何值时y随x的增大而减小？   2 5 82 3m my m x     二次函数的定义及基本性质1 例1 2 2 0, 5 8 2, m m m       2, 3. 2 3, m m m m         或解：（1）由题意得 解得 ∴满足条件的m=-3,这时二次函数的解析式为y=-x2+3. (2)抛物线y=-x2+3有最高点，该二次 函数有最大值，最大值是3. (3)当x>0时，y随x的增大而减小. x y O y=-x2+3 练习1： 1.抛物线y=(x-2)2+2的顶点坐标是（ ） A.(-2,2) B. (2,-2) C. (2,2) D. (-2,-2) 2.已知二次函数y=x2-x+c的顶点在x轴上，则c= . 3.二次函数y=x2+bx+3 的对称轴是直线x=2 ，则 b=_______. C 1 4 -4 函 数 二次函数y=ax2+bx+c(a,b,c是常数，a≠0) 图 象 a>0 a<0 性 质 开 口 向上，并向上无限延伸 向下，并向下无限延伸 对称轴 直线 顶 点 增减性 当 时y随x的增 大而减小；当 时，y随x的增大而增大. 当 时y随x的增大 而增大；当 时， y随x的增大而减小. 最 值 y xO xO 2 bx a   24( , ) 2 4 b ac b a a   2 bx a   2 bx a  2 bx a  2 bx a  24= 4 ac by a  最小值 24= 4 ac by a  最大值 y 抛物线y=ax2+bx+c (a≠0)与x轴的公共点是（-1，0）， （3，0），则这条抛物线的对称轴为_________. 解析 抛物线与x轴的两个交点是一对对称点.其实只要抛物线 上两点（x1，y0）、(x2，y0)的纵坐标相等，这两点就是一对d 对关于抛物线对称轴对称的对称点.对称轴计算公式是直 线 ,因此这条抛物线的对称轴是直线 .1 2 2 x xx   ( 1) 3 1 2 x     直线x=1 二次函数图象的对称性2 例2 练习2：已知二次函数y=ax2+bx+c中，函数y与自变量x的部分 对应值如下表： x … -1 0 1 2 3 … y … 10 5 2 1 2 … 则①抛物线的对称轴是 ； ②当y<5时，x的取值范围是 . ③在此抛物线上有两点A(3，y1)，B(4.5，y2)，试比较y1和y2的 大小：y1________y2(填“＞”“＜”或“＝”). 直线x=2 00时， x的取值范围是 . y x1-1 3 -10；③abc＞0；④当y＜0时，x＜-1或x＞3．其中正确的是 （ ） A.①② B. ①③ C.①④ D. ②③ x1 B C A -1 O y x=1C 例4 4 解析 ①2a＋b＝0, 想到对称轴 ,得b=-2a,故2a＋b＝0正确； ② 4a－2b＋c>0，想到当x=-2时结合图象可知y<0,故4a－2b＋c>0 不正确； ③abc＞0，由图象可知a<0,对称轴在y轴的右侧，根据 “左同右异”，则b>0,又易知c>0,故abc＞0不正确； ④当y＜0时， x＜-1或x＞3，根据对称性可知A点的坐标是（2，0），结合图象 可知当y＜0时，x＜-1或x＞3，故正确，所以选C. 1 2 bx a    知识点复习 抛物线y=ax2+bx+c中的符号问题: ① a的符号决定开口方向； ② a、b的符号共同决定对称轴的位置，“左同右异”； ③ c的符号决定抛物线与y轴的交点位置. 练习5： 已知二次函数y=ax2+bx+c(a ≠0)的图象如图所示，且关于x 的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论： ①b2-4ac>0; ②abc<0; ③m>2.其中正确结论的个数是（ ） A.0 B.1 C. 2 D. 3 x 2 O y D 练习6： 如图，函数y=ax2-2x+1和y=ax+a（a是常数，且a ≠0) 在同一平面直角坐标系的图象可能是（ ） xO y A O x y B xO y C xO y D A 二次函数与一元二次方程的关系 结合二次函数y=ax2+bx+c图象，解答下列问题： ①写出方程ax2+bx+c=0的根； ②写出不等式ax2+bx+c>0的解集； ③写出y随x的增大而减小的自变量x的取值范围； ④若方程ax2+bx+c=k有两个不相等的实数根， 求k的取值范围. x 4 O y -1 3 解析 本题结合图象从中发现信息进行解题. 5 例5 解：（1）由图象可知，函数y=ax2+bx+c的图象与x轴相交于 （-1,0），（3,0）两点.∴方程的根为x1=-1，x2=3； （2）由图象可知当-11; (4)要使得有ax2+bx+c=k两个不相等的实数根，即直线x=k与 二次函数图象有两个交点，∴k的取值范围为k<5. 练习7：已知抛物线y=ax2+bx+c的图象如图所示，则关于x的方程 ax2+bx+c-8=0的根的情况是（ ） A.有两个不相等的正实数根 B.有两个异号实数根 C.有两个相等的实数根 D.没有实数根 x 8 O y C 待定系数法求二次函数的解析式 x 4 O y -1 3 你能求出图中抛物线的解析式吗？ 解析 图象中提供了我们解题的很多信息， 如可知道抛物线与x轴的两个交点坐标是 （-1，0）和（3，0），还可以知道对称轴 是直线x=2及顶点坐标是(1,4). 你有几种方法可 以求这条抛物线 的解析式，你最 喜欢哪一种？ 例6 6 解：设抛物线的解析式为y=a（x-h）2+k. 由图象可知抛物线的对称轴为直线x=1，与x轴相交于点（- 1,0），（3,0），顶点坐标为（1,4）， ∴有y=a（x-1）2+4， 代入（-1,0）.∴a（-1-1）2+4=0，∴a=-1， ∴抛物线的解析式为y=-（x-1）2+4. 方法提示 知道顶点坐标，通常设顶点式y=a(x-h)2+k;知道抛物线 与x轴的两个交点坐标，通常设交点式y=a(x-x1)(x-x2);知道抛物线 上的三点坐标，可选用一般式y=ax2+bx+c,三种情况都可以时选用 最熟悉的方法. 练习8： 已知二次函数当x=1时，有最大值－6，且其图象过点(2， －8)，则二次函数的解析式是 .y=-2(x-1)2-6 综合应用—呈抛物线形状实物的几何探究 跳绳时，绳甩到最高处的形状可近似的看为抛物线，如图， 正在甩绳的甲、乙两名同学拿绳的手间距为4米，距地面均为1米， 丙、丁同学分别站在距甲拿绳的手水平距离1米、2.5米处，绳子 甩到最高处，刚好通过他们的头顶，已知丙同学的身高是1.5米. （1）请你算一算丁同学的身高. 1m 甲 乙 丁丙 2.5m 4m 1m (0,1) (4,1) (1,1.5) 7 例7 解得： ，所以抛物线解析式为 当x=2.5时，y=1.625.所以丁同学的身高为1.625米. 1m 甲 乙 丁丙 2.5m 4m 1m 解:如图建立平面直角坐标系，可设抛物线的解析式为y=ax2+bx+1 点（1,1.5）、（4,1）在抛物线上，得 (0,1) (4,1) (1,1.5) 1 1.5, 16 4 1 1, a b a b        1 2, 6 3 a b   21 2 1(1 4 6 3 y x x x    ≤ ≤ ）, （2）如果身高为1.5米的丙同学站在甲、乙同学之间,且离甲同 学的距离为s米, 要使绳子甩到最高处时超过他的头顶,请结合 图像,直接写出s的取值范围. 1m 甲 乙 丁丙 2.5m 4m 1m 10, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是 （ ） xO y A xO y B xO y C xO y D A 3.将二次函数y=2x2-1的图象沿y轴向上平移2个单位，所得到的图象 的函数解析式是 .y=2x2+1 4.二次函数y=ax2+bx+c的图象经过点(3,6)和(-1,6),则对称轴 为 .直线x=1 5.如图1，抛物线y=ax2+bx+c与x轴交于点A（1，0）、B（-3， 0）两点，与y轴交于点C（0,3）. （1）求该抛物线的解析式； （2）在该抛物线的对称轴上是否存在点Q，使得△QAC的周 长最小？若存在，求出点Q的坐标；若不存在，请说明理由. y=-x2-2x+3 Q（-1，2） xO y A C B 图1 xO y A C B 图2 Q 解：（1）由题设，将A（1，0）、B（-3，0）、C（0,3）代 入y=ax2+bx+c， 0, 9 3 0, 0, a b c b c c          ∴抛物线的解析式为y=-x2-2x+3； xO y A C B 图1 1, 2, 3. a b c 解得        （2）存在，理由如下： 作点C关于抛物线对称轴直线x=-1的对称点C’，由抛物线的 性质可知点C‘在抛物线上，点C’的坐标是（-2,3），连接点 C’A交抛物线的对称轴直线x=-1与点Q，点Q即为所求.设直 线C‘A的解析式为y=kx+m，代入（-2,3）和（0，1）可得 k=-1，m=1.所以Q的坐标为（-1,2）； xO y A C B 图2 Q C’