全国中学生物理竞赛课件13：波的几何描述与特征现象 37页

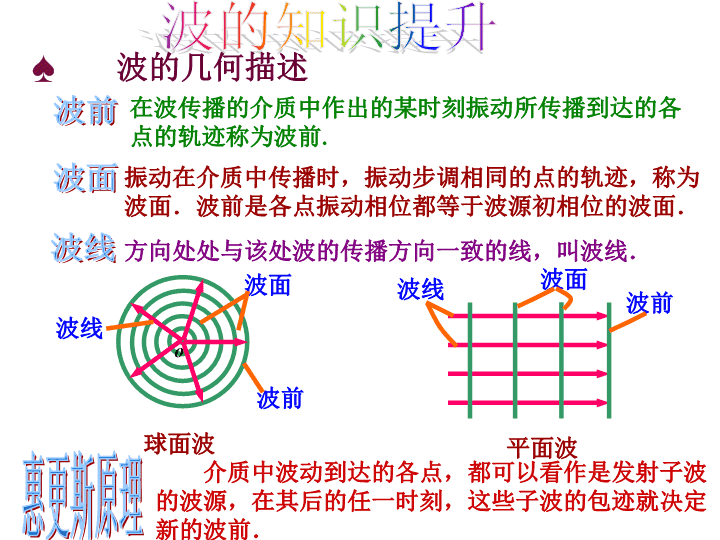
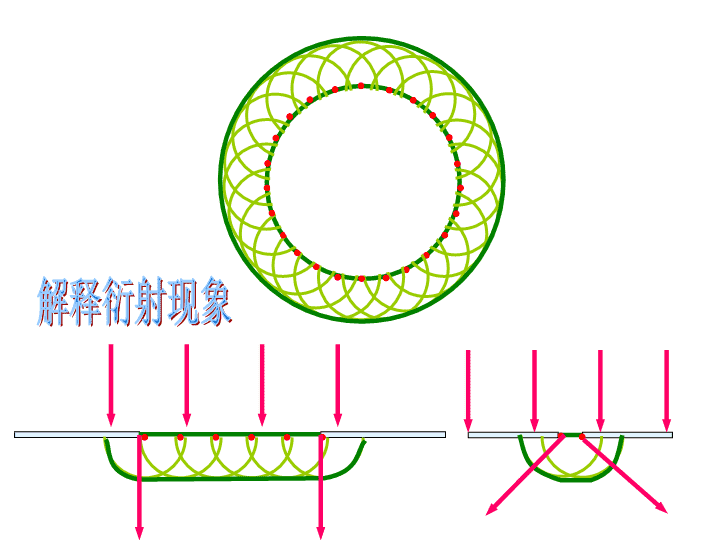
波的几何描述♠ 在波传播的介质中作出的某时刻振动所传播到达的各 点的轨迹称为波前. 振动在介质中传播时，振动步调相同的点的轨迹，称为 波面．波前是各点振动相位都等于波源初相位的波面． 方向处处与该处波的传播方向一致的线，叫波线． 球面波 平面波 波面 o 波线 波面波线 波前 波前 　　介质中波动到达的各点，都可以看作是发射子波 的波源，在其后的任一时刻，这些子波的包迹就决定 新的波前． 反射定律 M NA B A′ B′ i r    A B vt AB Rt AA B Rt ABB     i r  两种介质界面上的波现象♠ 折射定律 M NA B A′ B′ i r ri 1 2 sin sin v t v t AB i r    1 21 2 sin sin vi n r v    1v 2v A1 B A2 B2 i r M M A B1 N  N C C  緃tan 3 v t i v t    橫 i 60i   一平面波遇到两种介质的界面时发生反射，设入射波与反射 波的振动方向相同．如果入射波是一纵波，要使反射波是一横波，设纵波在介质 中的传播速度是横波传播速度的倍．问入射角为多少？ AB v t 子 A C Bφ φ 弹道波的几何描述如示: m5 AC V t 波 1sin 2 V v   波 子 30   设人在C处: 子弹与人的距离即为CB=10 m 子弹在离人5 m处以速度680 m/s水平飞过，当人听到子弹之啸 声时，子弹离人多远？设声速为340 m/s. 飞机超音速飞行，引起 圆锥面波，故飞机速度 v＝V/sin37 站在地面上的观测者发现一架飞机向他飞来，但听不到声音， 一直到看见飞机的方向和水平成37°角时，才听到轰呜声，若飞机沿水平直线飞 行，当时声速为336 m/s，飞机的速度是多少？ =560 m/s 依据惠更斯原理求解: M N r0 r O 0 0 N cv r n    M cv r n   0 0 c c r n rn    则   0 0 0 01 1 r r ca r a e r                即 0 01 r r c r r e c     取     0 0 0 0 0 r r a r r r r a r c         得 0 1 1 a r c    得 0r实际的地表大气密度满足 0 0 1a n     0 00 0 1 1 1 r n c            故  4.58 倍 假设大气折射率n与空气的密度有关系 ．式中a为常 数，ρ0为地球表面的大气密度，r0＝6400 km，c=8772 m，大气折射率随高度的 增加而递减．为使光线能沿着地球表面的圆弧线弯曲传播，地表的空气密度应是 实际密度的多少倍？已知地表空气的实际折射率n0=1.0003． 0 01 r r cn a e     依据惠更斯原理求解: M N h0 h O 0 h h h c c h n hn  由 0 0 0 0 0 0( ) ( ) c c n ah n a R h R h h h h                0 0 0 0 0 0n ah R h n ah a h R h h                 0 0 0n ah h a h R h     0 0 1 2 n h R a       R 某行星上大气的折射率随着行星表面的高 度h按照n＝n0－ah的规律而减小，行星的半径为R，行星 表面某一高度h0处有光波道，它始终在恒定高度，光线沿 光波道环绕行星传播，试 高度h0． 驻波♠ 两列沿相反方向传播的振幅相同、频率相同的波 叠加时，形成驻波． 静止不动的波节和振幅最大的波腹相间，但波形 不向任何方向移动， 从驻波的成因来看，驻波是一种干涉现象：波节与波 腹分别是振动抵消与振动最强区域，它们的位置是不 变的； 从驻波上各质点的振动情况来看，实际上是有限 大小的物体上有相互联系的无数质点整体的一种 振动模式． 弦线或空气柱以驻波的模式振动，成为声源，并 将这种振动形式在周围空气中传播，形成声波． 示例 规律 拍♠ 两个同方向的简谐运动合成时，由于频率 略有差别，产生的合振动振幅时而加强时 而减弱的现象叫拍．在单位时间内合振幅 的极大值出现的次数叫做拍频． 1 22 2 2f f T     1 2 1 f f T   t＝T/4 t＝0,T t＝T/2 t＝3T/4 t＝0t＝T/2t /4t＝3 4t T 返回 如图所示，一端固定在台上的弦线，用支柱支撑其R点和S点， 另一端通过定滑轮吊一个1.6 kg的重物，弹拨弦的RS部分，使其振动，则R、S点为波节， 其间产生三个波腹的驻波，这时，如在弦的附近使频率为278 Hz的音叉发音，则5 s内可 听到10次拍音，换用频率稍大的音叉，则拍音频率减小．测得RS＝75.0 cm，求该驻波的 波长、频率及弦线的线密度． 由驻波成因知该波波长为: m 2 50.0 3 L   弦振动频率与音叉振动频率差产生拍: 1 2f f f  1 10 278 5 f  1 280f  Tv  由 mg kg/m2 1.6 9.8 140    kg/m30.8 10  R S 规律 试手18 问题 一个脉冲波在细绳中传播， 若绳的线密度为ρ，绳中张力为T试求 脉冲波在绳上的传播速度． v v  r v TT m r     2 2 sin 2 vT m r    v T   返回 将一根长为100多厘米的均匀弦线沿水平的x轴放置，拉紧并 使两端固定．现对离固定的右端25 cm处（取该处为原点O，如图1所示）的弦上施加一个 沿垂直于弦线方向（即y 轴方向）的扰动，其位移随时间的变化规律如图2所示．该扰动 将沿弦线传播而形成波（孤立的脉冲波）．已知该波在弦线中的传播速度为2.5 cm/s，且 波在传播和反射过程中都没有能量损失． ⒈试在图1中准确地画出自O点沿弦线向右传播的波在t＝2.5 s时的波形． ⒉该波向右传播到固定点时将发生反射，反射波向左传播．反射点总是固定不动的．这 可看成是向右传播的波和向左传播的波相叠加，使反射点的位移始终为零．由此观点出发， 试在图1中准确地画出t＝12.5 s时的波形图． 图13-12-2图1 解答 图2 2.5T  s 6.25vT   m 6.25 波到达右端经 再经2.5S,即t=12.5s时 y/cm x/cm 5 10 15 20 25 0.10 0.05 -0.10 -0.05 0 18.75 再经0.5S,即t=10.5s时 18.756.25 y/cm x/cm 5 10 15 20 25 0.10 0.05 -0.10 -0.05 0 25 2. 10 5 t   s 脉冲波形成经 2.5t T  s 23.75 一列横波在弦线上传播，到固定端时被反射，反射波在弦线上沿 反方向传播而形成驻波．反射时波长、频率、振幅均不变，但反射波与入射波使反射点的 振动相差半个周期，相当于原波损失半个波再反射．在图中已画出某时刻入射波B，试用 虚线画出反射波C，用实线画出驻波A． B C A 当声波频率f＝7 Hz时，波长 : 347.2 m 49.6m 7 v f     那么井深至少为波长四分之一即12.4 m 时，空气柱与音叉可发生共鸣 这样一个井的深度，还可能与频率大于 7Hz、波长短于49.6 m、但波长的 2 1 4 n 倍恰等于12.4 m的某些声波发生共鸣! 有一口竖直井，井底有水，它可与f≥７Hz的某些频率发生共 鸣．若声波在该井里的空气中的传播速度为347.2 m/s，试问这口井至少有多深？ 标准声频率为250 Hz，拍频1.5 Hz，粘上橡皮后音 叉频率减小，与标准声的拍频增大，可知音叉原频 率为比标准声频率低，为248.5 Hz 由共鸣时空气柱长度知 1.03 0.34 2    1.38m  343m/sV f 則 音叉与频率为250 Hz的标准声源同时发音，产生1.5 Hz的拍 音．当音叉叉股粘上一小块橡皮泥时，拍频增大了．将该音叉放在盛水的细管口，如图所 示，连续调节水面的高度，当空气柱高度相继为0.34 m和1.03 m时发生共鸣．求声波在空 气中的声速，画出空气柱中的驻波波形图． V Vf T f V     (1 )V v V v v f V f VT       V Vf VT uT V f V u       V vf VT u V v f uT V     设定： 波源相对于介质的速度u；观察者相对于介质的速度v；波在介质中速度V；观察者接收到的频率f ′；波源频率f． ． ㈡波源固定，观察者以v向着波源或背离波源运动 ． ㈢波源以速度u相对于介质向着或背离观察者运动，观察者静止 uT 如图，此时相当于波长缩短或增长为 ，故 ． ㈣波源与观察者同时相对介质运动 此时相当于波以速度 V±v通过观察者，故 ㈠波源与观察者相对介质静止 多普勒效应♠ λ u  uT 设“哆”音频率为f1；低“咪”音频率为f2，有 1 0 V vf f V u    2 0 V vf f V u    1 2 (1200 80)(1200 ) 8 (1200 )(1200 80) 5 f u f u       由 km/h200u得 对相向而行的乘客： 对静止的路旁观察者： V f V uV u Vf V u V u     前 后 由         V v f V v V uV u V vf V v V u V u         超前 超后 由 7 5  对同向而行的乘客： 49 40  车以80 km/h速度行驶，从对面开来超高速列车，向背后奔驶而 去．此间超高速车所发出的汽笛声开始若听取“哆”音，后来听到的则是降低的“咪”音 （假定“哆”音和“咪”音的频率之比为8/5）．设声速为1200 km/h，则超高速列车的时 速是多少？这时，对站在路旁的人而言，超高速列车通过他前后声音的频率之比是多少？ 而对与超高速列车同向行驶、车速为80 km/h的车上乘客而言，他被超高速列车追过前后 所闻汽笛声音的频率之比又是多少？ 观察者接收到的频率先高后低， 说明声源与观察者先接近后远 离！作出示意图: cosAu v  A M B h α β v uA v uB cosBu v  1 0cos Vf f V v    2 0cos Vf f V v    11cos 40   33cos 80   由几何关系：  cot cotvt h    代入数据后得 m1096h cot cot vth     飞机在上空以速度v＝200m/s做水平飞行，发出频率为f0＝2000 Hz的声波．静止在地面上的观察者测定，当飞机越过观察者上空时，观察者４s内测出的 频率从f1＝2400 Hz降为f2＝1600 Hz．已知声波在空气中速度为V＝330 m/s．试求飞机 的飞行高度． 这是测定宇宙中双星的一种方法 (1) 由于B星发出的光波波长在P点位比Q点位短，可 知在P点位光源是朝着地球运动的，故B星公转的方向 为沿图中逆时针方向 P Q A B P Q B A ⑵ 0vT v c      可得v＝42 km/s 88 40 10 kmvtR    ⑶ 有A、B两个星球．B星以A星为中心做匀速圆周运动，如 图．由于星球离地球非常远，而且地球位于B星的轨道平面上，所以从地球上 看过去，B星好象在一条直线上运动．测得B星从P点移动到Q点需要6.28×107 s．由于多普勒效应，在测定B星发出的光的波长时发现，当B星位于P点时比 位于A点时短0.68×10-10 m，位于Q点时则比A点长同样的值．若位于A点时的 波长测量值为4861.33×10-10 m，光速c＝3.0×108 m/s．求⑴B星公转的方向; ⑵ B星的公转速度是多少km/s？ ⑶圆周轨道的半径． 设人造卫星朝地面接收站方向运动的速度为u， 此即波源移动速度，由于波源向着观察者运 动，接收到的频率变大，由 cf f f c u     可得 8 8 2400 3.0 10 m/s 10 2400 cfu c f f         7200m/s 某人造地球卫星发出频率为10 8 Hz的无线电讯号，地面接收 站接收到的讯号频率增大了2400 Hz．已知无线电讯号在真空中的传播速度为c ＝3.0×108 m/s，试估算人造卫星朝地面接收站方向的运动速度． 接收到来自乐队的频率 1 0 330 5 330 f f u    来自广播声的频率 2 0 330 5 330 f f  335 335 4( ) 440 330 330 3u     則 U≈1 m/s 在单行道上，交通川流不息，有一支乐队沿同一方向前 进．乐队后面有一坐在车上的旅行者向他们靠近，这时，乐队正同时奏出频率 为440 Hz的音调．在乐队前面街上有一固定广播设施做现场转播．旅行者发现 从前面乐队直接听到的声音和从广播中听到的声音相结合产生拍，并测出三秒 钟有四拍．利用测速计可测出车速为18 km/h．试计算乐队行进的速度．已知 在这个寒冷的天气下，声速为330 m/s． 一波源振动频率为2040 Hz，以速度vs向墙壁接近，如图，观 测者在A点所得的拍频 =3 Hz，设声速为340m/s，求波源移动的速度vs．如 波源没有运动，而以一反射面代替墙壁，以速度=0.2 m/s向观察者A接近，所 得到的拍频为 =4 Hz，求波源的频率．    ⑴A点从声源直接接收到的声波频率 1 0 s Vf f V v   经墙反射后的声波频率 2 0 s Vf f V v   则 0 0 s s V Vf f V v V v      观测者 波源 A S 续解 代入题给数据 2 2 2 340 3 2040 340 s s v v     2 2 2680 340 0,s sv v   =0.25m/ssv ⑵若反射面移动，则A点从声源直接接收到的声波频率 1f f  反射面接收到的波频率 2 V v f f V   反射到A接收到的波频率 2 2 V vVf f f V v V v          则 2 0.24 340 0.2 V v f f f V v             3398Hzf  u Rω φ θ 声源移动速度为Rω，相对观察 者接近或背离速度设为u， 0sin( ) Vf f V R       有 2 sin sin( ) r r      又 ( ) 90   当 时 f  有最值, 此时θ＝60°或θ＝300° 554Hzf 最大 456Hzf 最小 如图，音叉P沿着半径r＝8m的圆以角速度ω=4rad/s做匀速圆 周运动．音叉发出频率为f0＝500 Hz的声波，声波的速度为v＝330 m/s．观察 者Ｍ与圆周共面，与圆心Ｏ的距离为d＝2r． 试问当角θ为多大时，观察到的频率为最高或最低，并求其数值． 到了晚上，地面辐射降温使空气层中产生温度梯度，温度随高 度递增，这导致声速v随高度y变化，假定变化规律为： ．式中v0 是地面（y＝０处）的声速，a为比例系数．今远方地面上某声源发出一束声波， 发射方向与竖直成θ角．假定在声波传播范围内 <<１，试求该声波在空间传 播的轨迹，并求地面上听得最清晰的地点与声源的距离S ． 2 2 0(1 )v v a y  ay 由于声速沿y轴 递增，折射角θi 逐渐增大，开始 一段声传播的径 迹大致如图! 夜间 寂静区 寂静区 白天 y i x y ０ 0v 0 第i层 1  2 x 根据折射定律: 1 1 2 2 0 0 1 1 1 1 sinsin sin, , , , sin sin sin i i i i vv v v v v          0 0 sin sini i v v  可得 声波波线即声传播轨迹! 1 续解 第i层声波波线视为直线,有 2 1cot 1 sini i y x        2 0 2 2 0 1 sini v v    查阅  22 2 2 0 1 1 1 sina y     2 02 2 0 1 1 sin sin 1 2a y      2 2 2 0 0 1 1 2 sin sin a y      2 20 2 0 0 cos 21 sin cos a y      2 2 0 2 0 2cot 1 cos a y    2sin x 2 2 2 2 0 2 sin cos a y x  由 0cos sin 2 y x a  可得波线方程为 续 解 0cos sin 2 y x a  对待定方程 求斜率 2  0 0 2cos sincos 2 2lim 2 x x x x x xa           0 0 0 0 sin sincos lim lim 2x x y x x xy x xa                0cos cos 2 x a    0cot cos x  0 2 sin a    于是得声传播轨迹方程: 0 0 cos 2sin sin2 a xy a           可知地面上听得最清点距声源 0 0 2 sin a x     0 1 sin 2 x S a     比较 在海洋中声速随深度、温度和含盐量变化．已知声速 随深度变化规律如图，最小声速出现在海洋表面与海底之间．坐 标原点取在声速最小处，za、zb分别表示海面和海底的坐标．则 声速v与z的关系为 其中b为常量．今在x=0，z=0处放置一声源S，在xz平面内，从S发出 的声波的传播方向用初始发射角θ0表示．声速的不均匀将导致波 射线的弯曲．试证明在zx平面内声波的初始轨迹为圆，并求出其 半径． 0 0 0 ( 0) ( 0) ( 0) v bz z v v z v bz z        O za zb vo v z 在xz平面将海水分成与x轴平行的 n薄层(n→∞)，各层的波速可视为不变， 波在各层传播时遵循折射定律，第i层 的波速为vi，波在该薄层两界面上的折 射角为θi，在下一层的折射角为θi+1， 每经过一薄层，声波传播方向改变 Δθ=θi+1－θi 续解 由折射定律： △ z △s 1 i  i  i 1 i 0 0 0 0 sin si sin sin n i i i iv v v v       对第i薄层海水有 1 cosi i iv v b z b s          0 1 0 sin sin cos sin i i i v b s         0 1 1 0 (2cos sin ) cos sin 2 2 i i i i i v b s             0 0sini v R b s      2 i cos i 设岸的坡度为m，水深h，下限水深度为h0，此 处水波速率v0并平行于岸，y为离岸距离，又 v=kh，波线设为如图 y 岸 0 Δy v0  i  i 根据折射定律: 0 0 sin sin i iv v    由几何关系: cos iy S      1 0 1 0 sin sin sin i i i i v v vvy km km km            0 0 2cos sin sin 2i v km      cos i vi vi+ 1 走在岸边，总可以看到水波平行于岸边滚滚而来．设 水波的速率与水深成正比，岸的斜度为常数，计算水波的轨迹． ΔS 2  0 0sin v R km S     