苏教版数学九年级上册课件2-6正多边形与圆 22页

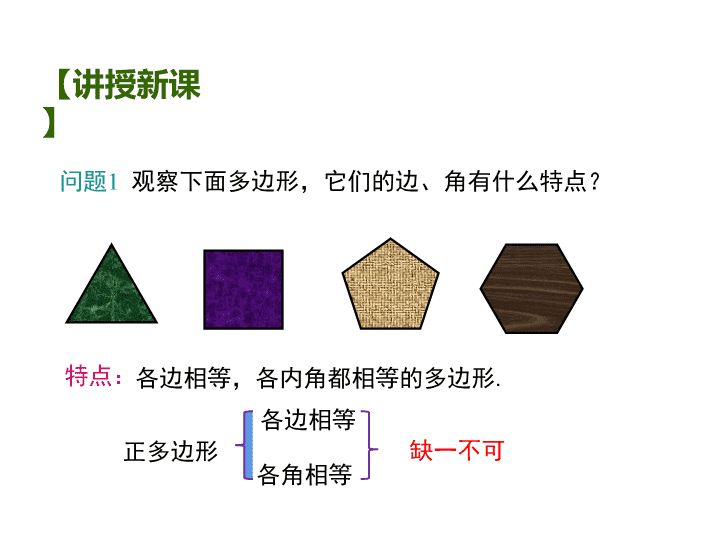
2.6 正多边形与圆 观看大屏幕上这些美丽的图案,都是在日常生活中我们经 常能看到的.这些图案是由哪些图形组成的？ 【导入新课】 问题1 观察下面多边形，它们的边、角有什么特点？ 特点：各边相等，各内角都相等的多边形. 正多边形 各边相等 各角相等 缺一不可 【讲授新课】 问题2 画出下列各正多边形的对称轴，看看能发现什么 结果？ 正n边形都是轴对称图形，都有n条对称轴，且这些对称轴 都交于一点. O A B CD 问题3 以正四边形为例,根据对称轴的性质，你能得出什 么结论？ E F G H EF是边AB、CD的垂直平分线， ∴OA=OB，OD=OC. GH是边AD、BC的垂直平分线， ∴OA=OD；OB=OC. ∴OA=OB=OC=OD. AC是∠DAB及∠DCB的角平分 线，BD是∠ABC及∠ADC的角 平分线，∴OE=OH=OF=OG. O A B CD E F G H 将点O到正四边形的各个顶点的 距离记作R，那么以O为圆心， R为半径的圆就过正四边形的各 个顶点，它是该正四边形的外 接圆. R 将点O到正四边形的各条边的距 离记作r，那么以O为圆心，r为 半径的圆就与正四边形的各条 边都相切，它是该正四边形的 内切圆. r 想一想 其它的正多边形是不是也都有一个外接圆和一个内 切圆？ 任何正多边形都有一个外接圆和一个内切圆. O A B CD E F G H R r 概念学习 正多变形外接圆和内切圆有公共 的圆心，称其为正多边形的中心. 外接圆的半径叫做正多边形的半 径. 内切圆的半径叫做正多边形的边 心距. 正多边形每一条边对应所对的外接圆的圆心角都相等， 叫做正多边形的中心角. 把☉O进行5等分,依次连接各等分点得到五边形ABCDE . · A O E DC B 这个五边形ABCDE是正五边形吗？简 单说说理由. 探究归纳 ①     ___ ___ ___ ___AB BC CD DE AE ② AB____BC____CD____DE____AE. ③ ∠A___∠B___∠C___∠D___∠E. ＝＝ ＝ ＝ ＝＝ ＝ ＝ ＝＝ ＝ ＝ 把圆分成n（n＞2）等份，依次连接各分点所得的多边形 就是这个圆的一个内接n边形. 例1 利用尺规作图，作出已知圆的内接正方形和内接正 六边形. 解：内接正方形的做法： （1）用直尺作圆的一条直径AC； A CO （2）作与AC垂直的直径BD； B D （3）顺次连接所得的圆上四点. 四边形ABCD即为所求作的正方形. 【例题讲解】 O 解：内接正六方形的做法： （1）用直尺作圆的一条直径AD； （2）以点A为圆心，OA为半径作圆， 与⊙ O交于点B、F； （4）顺次连接所得的圆上六点. 六边形ABCDEF即为所求作的正六边形. A D B F （3）以点D为圆心，OD为半径作圆， 与⊙ O交与点C、E. C E 如图，已知半径为4的圆内接正六边形ABCDEF： ①它的中心角等于 度 ； ② OC BC (填＞、＜或＝）； ③△OBC是 三角形； ④圆内接正六边形的面积是 △OBC面积的 倍. ⑤圆内接正六边形ABCDEF的面积:___________. C DO B EF A P 60 = 等边 6 填一填 24 3 想一想 问题1 正n边形的中心角怎么计算？ C DO B EF A P 360 n  问题2 正n边形的边长a，半径R，边 心距r之间有什么关系？ a R r 2 2 2( ) . 2 aR r  问题3 边长a，边心距r的正n边形的面积如何计算？ 1 1 . 2 2 S nar lr  其中l为正n边形的周长. 例2 有一个亭子,它的地基是半径为4 m的正六边形,求 地基的周长和面积 (精确到0.1 m2). C DO EF A P 抽象成 【例题讲解】 利用勾股定理,可得边心距 2 24 2 2 3.r    亭子地基的面积 4m OA B C D EF M r 解：过点O作OM⊥BC于M. 21 1 24 2 3 41.6(m ). 2 2 S l r      在Rt△OMB中,OB＝4, MB＝ 4 2 2 2 BC   ， 亭子地基的周长l=6×4=24(m) 2.作边心距，构造直角三角形. 1.连半径，得中心角； OA B C D EF R M r · 圆内接正多边形的辅助线 方法归纳 O 边心距r 边长一半 半径R C M 中心角一半 正多边 形边数 半径 边长 边心距 周长 面积 3 4 1 6 2 3 3 1. 填表 2 1 2 3 3 3 2 2 8 4 2 2 12 6 3 2. 若正多边形的边心距与半径的比为1:2，则这个多边形 的边数是 .3 【练习】 4. 要用圆形铁片截出边长为4cm的正方形铁片，则选用的圆形 铁片的直径最小要____cm. 也就是要找这个正 方形外接圆的直径 4 2 3.如图是一枚奥运会纪念币的图案，其形状近似看作为 正七边形，则一个内角为 ___度.（不取近似值） 4128 7 拓广探索 如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN. (1)求图①中∠MON=_______;图②中∠MON= ; 图③中∠MON= ; (2)试探究∠MON的度数与正n边形的边数n的关系. A B C D E A B C D . A B C M N M N M N OO O 90 ° 72 ° 360MON n    120 ° 图① 图② 图③ 正多边形 和圆 正多边形和 圆 的 关 系 正多边形的 有 关 概 念 正多边形的 有 关 计 算 添加辅助线的方法： 连半径，作边心距 任何正多边形都有一个 外接圆和一个内接圆 中心 半径 边心距 中心角 把圆分成n(n＞2）等份，依次连接各分 点所得的多边形是这个圆的内接正n边形. 【小结】