华师版九年级上册数学同步课件-第24章-24仰角、俯角问题 10页

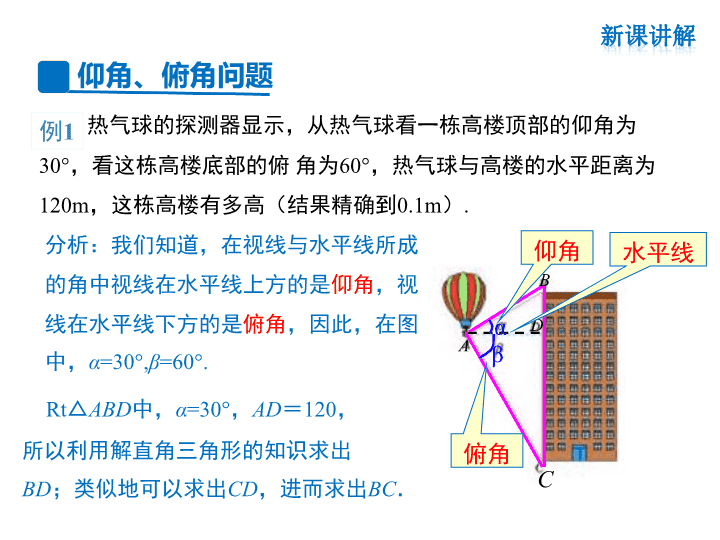
第24章 解直角三角形 24.4 解直角三角形 第2课时 仰角、俯角问题 问题1： 在三角形中共有几个元素？ 问题2 ： 解直角三角形的应用问题的思路是怎样？ 热气球的探测器显示，从热气球看一栋高楼顶部的仰角为 30°，看这栋高楼底部的俯 角为60°，热气球与高楼的水平距离 为120m，这栋高楼有多高（结果精确到0.1m）. 分析：我们知道，在视线与水平线所成 的角中视线在水平线上方的是仰角，视 线在水平线下方的是俯角，因此，在图 中，α=30°,β=60°. Rt△ABD中，α=30°，AD＝120， 所以利用解直角三角形的知识求出 BD；类似地可以求出CD，进而求出BC． A B C Dα β 仰角 水平线 俯角 仰角、俯角问题 例1 解：如图，a = 30°,β= 60°， AD＝120． tan tan   BD CD,AD AD tan 120 tan30     BD AD 3120 40 33    tan 120 tan 60CD AD      120 3 120 3   40 3 120 3BC BD CD     160 3 277.1  即这栋楼高约为277.1m. A B C Dα β ， ， . . 建筑物BC上有一旗杆AB，由距BC 40 m 的D处观察旗杆顶部A的仰角54°，观察底部B 的仰角为45°，求旗杆的高度（精确到0.1m）. A B CD 40m 54°45° A B CD 40m 54°45°解：在等腰三角形BCD中∠ACD=90°， BC=DC=40 m. 在Rt△ACD中 tan ACADC DC   tanAC ADC DC    tan54 40 1.38 40 55.2     ∴AB=AC－BC=55.2－40=15.2. 即旗杆的高度为15.2 m. ， . 例2 1.如图1，在高出海平面100米的悬崖顶A处，观测海平面上 一艘小船B，并测得它的俯角为45°，则船与观测者之间的 水平距离BC=_________米. 2.如图2，两建筑物AB和CD的水平距离为30米，从A点测得 D点的俯角为30°，测得C点的俯角为60°，则建筑物CD 的高为_____米. 100 20 3 图1 图2B C B C 解：依题意可知，在Rt∆ADC中 所以树高为19.2+1.72≈20.9(米) 3.为测量松树AB的高度，一个人站在距松树15米的E处，测 得仰角∠ACD=52°，已知人的高度是1.72米，求树高(精确 到0.1米）. A D BE C   tan tan52 15 1 280 15 19 2          AD ACD CD . . 米 4.如图3，从地面上的C、D两点测得树顶A仰角分别是 45°和30°，已知CD=200米，点C在BD上，则树高AB 等于 （根号保留）． 5.如图4，将宽为1cm的纸条沿BC折叠，使∠CAB=45°， 则折叠后重叠部分的面积为 （根号保留）．  100 1 3 米 图3 图4 cm2 2 2 铅 直 线 水平线 视线 视线 仰角 俯角 ★1.在进行测量时，从下向上看，视线与水平线的夹角叫做仰角； 从上往下看，视线与水平线的夹角叫做俯角. ★3.认真阅读题目，把实际问题去掉情境转化为数学 中的几何问题.把四边形问题转化为特殊四边形（矩形或 平行四边形）与三角形来解决. ★2.梯形通常分解成矩形和直角三角形（或分解成平 行四边形与直角三角形）来处理.