华师版九年级上册数学同步课件-第24章-24 特殊角的三角函数值 13页

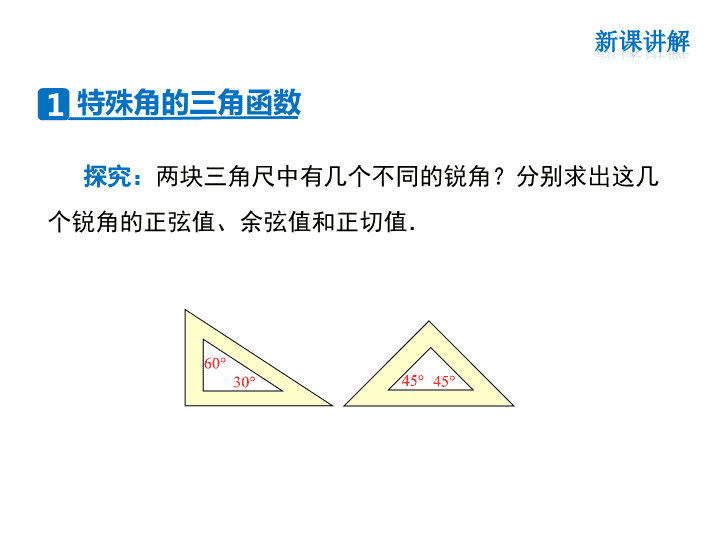
第24章 解直角三角形 24. 3 锐角三角函数 第2课时 特殊角的三角函数值 1.在Rt△ABC中，∠C=90°，cosA= , BC=8，则 AB=_______，AC=_______，sinB=_______，△ABC的周长 是______. 2.在Rt△ABC中，∠C=90°，∠B=45°，则∠A=_____，设 AB=k（k≠0），则AC=_____，BC=_____，sinB= sin45°=____， cosB =cos45°=____，tanB= tan45°= ____. 5 3 10 6 5 3 24 45° 2 2 k 2 2 k 2 2 2 2 1 探究：两块三角尺中有几个不同的锐角？分别求出这几 个锐角的正弦值、余弦值和正切值． 30° 60° 45°45° 特殊角的三角函数1 设30°所对的直角边长为a，那么斜边长为2a， 另一条直角边长＝  2 22 3a a a  1sin30 2 2 a a    3 3cos30 2 2 a a   3tan30 33 a a   30° ， ， ， . 3 3sin 60 2 2 a a    1cos60 2 2 a a   3tan 60 3a a   设两条直角边长为a，则斜边长＝ 2 2 2a a a  2cos45 22 a a   tan 45 1a a   2sin 45 22 a a    60° 45° ， ， . ， ， . ， 30°、45°、60°角的正弦值、余弦值和正切值如下表： 锐角a 三角函数 30° 45° 60° sin a cos a tan a 1 2 2 2 3 2 2 2 1 2 3 3 2 3 3 1 求下列各式的值： （1）cos260°＋sin260° （2）    45tan45sin 45cos  解： （1） cos260°＋sin260° 22 2 3 2 1           ＝1.    45tan45sin 45cos （2） 12 2 2 2  ＝0. 特殊三角函数值的运用2 例1 操场里有一个旗杆，老师让小明去测量旗杆高度，小明 站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线 的夹角为30°，并已知目高为1.65米．然后他很快就算出旗 杆的高度了. 1.65米 10米 ? 30° 你想知道小明怎样算出的吗？ 例2 1.如图，在△ABC中，∠A=30°， 求AB. 3tan , 2 3,2B AC  A B C D 解：过点C作CD⊥AB于点D ∠A=30°，2 3AC  1sin 2 CDA AC   1 2 3 32CD    3cos 2 ADA AC   3 2 3 32AD    3tan 2 CDB BD   23 2 3 BD    3 2 5AB AD BD      ， . ， . ， . ， . . 2.求下列各式的值： （1）1－2 sin30°cos30° （2）3tan30°－tan45°+2sin60° （3）   30tan 1 60sin1 60cos  解： （1）1－2 sin30°cos30° 1 31 2 2 2     31 2   （2）3tan30°－tan45°+2sin60° 3 33 1 23 2      3 1 3   2 3 1  cos60 1(3) 1 sin 60 tan30     1 12 3 31 2 3    2 3 3   2 . 3. 在Rt△ABC中，∠C＝90°， 求∠A、∠B的度数． 21,7  ACBC B A C 7 21 解： 由勾股定理，得 7 1sin 22 7 BCA AB        2 22 2 21 7 28 2 7AB AC BC      ∴ ∠A=30° ∠B = 90°－ ∠ A = 90°－30°= 60° ， ， ， . ★30°、45°、60°角的正弦值、余弦值和正切值如下表： 锐角a 三角函数 30° 45° 60° sin a cos a tan a 1 2 2 2 3 2 2 2 1 2 3 3 2 3 3 1 对于sin α与tan α，角度越大，函数值也越大；（α为锐角） 对于cos α，角度越大，函数值越小.