九年级数学上册第五章投影与视图2视图教案新版北师大版 3页

‎2　视图 ‎1．会从投影的角度理解视图的概念，能说出基本几何体的三视图的形状．会画三棱柱、四棱柱的三视图．能根据几何体的俯视图画出其主视图和左视图．‎ ‎2．经历探索简单几何体及棱柱的三视图的过程，培养学生的空间想象能力及画图能力．‎ ‎3．经历由几何体的俯视图探索主视图和俯视图的过程，进一步发展学生的推理能力和空间感．‎ 重点 掌握三视图的画法，能进行几何体和三视图之间的相互转化．‎ 难点 几何体与三视图之间的相互转化．‎ 一、复习导入 教师：什么是投影？什么是中心投影？什么是平行投影？什么是正投影？‎ 教师指名学生回答．‎ 二、探究新知 ‎1．主视图、俯视图、左视图的概念 课件出示教材第134页图5－12，提出问题：‎ ‎(1)假设有一束平行光线从正面投射到图中的物体上，你能想象出它在这束平行光线下的正投影吗？把你想象的正投影画出来，并与同伴交流．‎ ‎(2)如果平行线光线从左面投射到图中的物体上，情况又如何？如果平行光线从上面投射到图中的物体上呢？‎ 学生独立画图，教师巡视指导，并讲解：‎ 用正投影的方法绘制的物体在投影面上的图形，叫做物体的视图．通常我们把从正面得到的视图叫做主视图，从左面得到的视图叫做左视图；从上面得到的视图叫做俯视图．(正视图、左视图、俯视图统称为三视图)‎ ‎2．主视图、左视图、俯视图的画法 学生活动：请同学们拿出事先准备好的直三棱柱、直四棱柱，根据你所摆放的位置经过想象，再抽象出这两个直棱柱的主视图、左视图和俯视图．‎ 学生分四人小组，合作学习．观察、画图、交流，上台演示．‎ 教师：请你将抽象出来的三种视图画出来，并与同伴交流．‎ 指名同学在黑板上画出其中一个几何体的主视图、左视图和俯视图，完成后提出问题：你认为他画得对不对？谈谈你的看法．‎ 学生积极举手回答，发表自己的看法．‎ 教师：当你手中的两个直棱柱摆放的角度变化时，它们的三种视图是否会随之改变？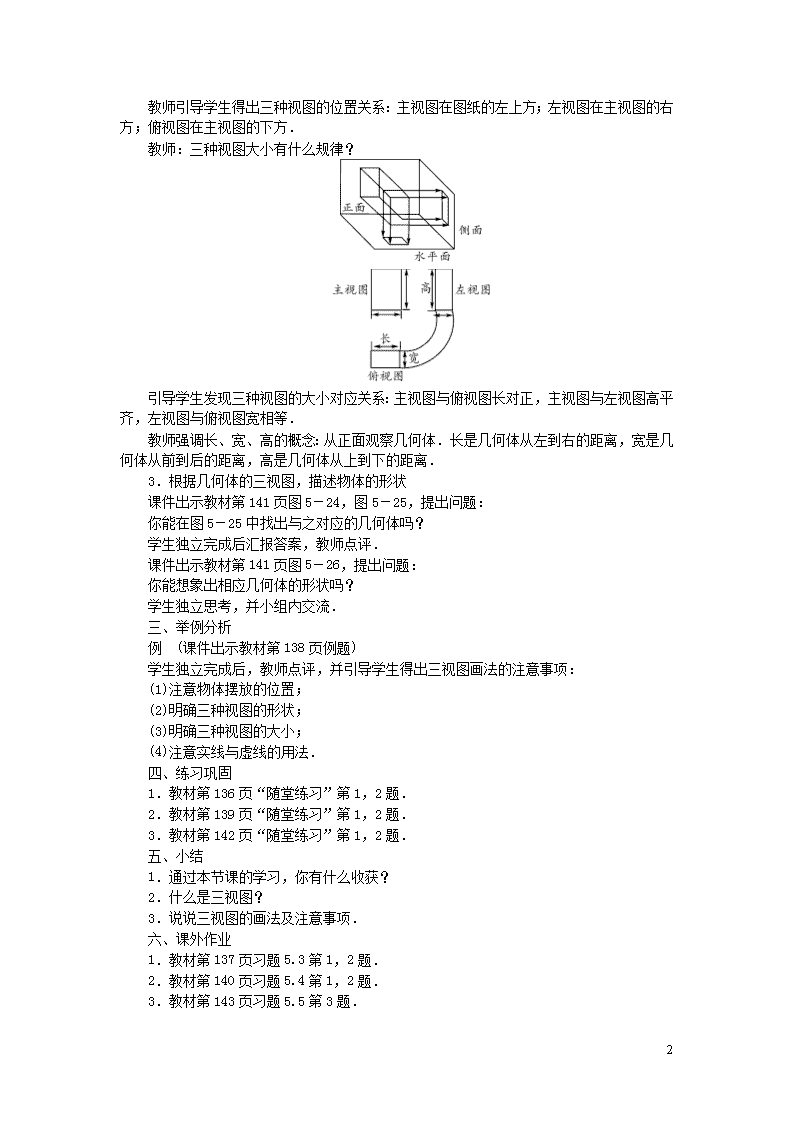试一试．‎ 学生动手操作演示，教师巡视．‎ 课件出示一个长方体，提出问题：请画出这个长方体的主视图、左视图、俯视图．‎ 学生独立完成后，教师课件演示：对几何体进行正投影得到三视图．‎ 教师：将水平面、侧面、正面展开到同一平面，观察得到三种视图有什么位置关系？‎ 3‎ 教师引导学生得出三种视图的位置关系：主视图在图纸的左上方；左视图在主视图的右方；俯视图在主视图的下方．‎ 教师：三种视图大小有什么规律？‎ ‎ ‎ 引导学生发现三种视图的大小对应关系：主视图与俯视图长对正，主视图与左视图高平齐，左视图与俯视图宽相等．‎ 教师强调长、宽、高的概念：从正面观察几何体．长是几何体从左到右的距离，宽是几何体从前到后的距离，高是几何体从上到下的距离．‎ ‎3．根据几何体的三视图，描述物体的形状 课件出示教材第141页图5－24，图5－25，提出问题：‎ 你能在图5－25中找出与之对应的几何体吗？‎ 学生独立完成后汇报答案，教师点评．‎ 课件出示教材第141页图5－26，提出问题：‎ 你能想象出相应几何体的形状吗？‎ 学生独立思考，并小组内交流．‎ 三、举例分析 例　(课件出示教材第138页例题)‎ 学生独立完成后，教师点评，并引导学生得出三视图画法的注意事项：‎ ‎(1)注意物体摆放的位置；‎ ‎(2)明确三种视图的形状；‎ ‎(3)明确三种视图的大小；‎ ‎(4)注意实线与虚线的用法．‎ 四、练习巩固 ‎1．教材第136页“随堂练习”第1，2题．‎ ‎2．教材第139页“随堂练习”第1，2题．‎ ‎3．教材第142页“随堂练习”第1，2题．‎ 五、小结 ‎1．通过本节课的学习，你有什么收获？‎ ‎2．什么是三视图？‎ ‎3．说说三视图的画法及注意事项．‎ 六、课外作业 ‎1．教材第137页习题5.3第1，2题．‎ ‎2．教材第140页习题5.4第1，2题．‎ ‎3．教材第143页习题5.5第3题．‎ 3‎ 本节课的内容为视图，主要是通过对由实物抽象出几何体的过程，发展学生的空间想象能力．在教学过程中通过具体活动，积累学生的观察、想象物体投影的经验．在画实物的视图时，必须首先对实物进行合理的抽象，即把实物抽象成相应的几何体，在此基础上再画其视图．而且也会根据三视图描述几何体的形状．通过观察、操作、猜想、讨论、合作等活动，使学生体会到三视图中位置及各部分之间大小的对应关系，积累数学活动的经验．在应用数学解决生活中问题的过程中，品尝成功的喜悦，激发学生应用数学的热情．培养学生自主学习与合作学习相结合的学习方式，使学生体会从生活中发现数学．‎ 3‎