2021人教版数学九年级上学期期末测试试题及答案（三套） 63页

九年级数学上学期期末检测试题（一） 一、选择题（本大题共 8 小题，共 24．0 分） 1．方程 2 0x x  的解是（ ） A． 0x  B． 1x  C． 1 0x  ， 2 1x  D． 1 0x  ， 2 1x   2．如图所示的物体组合，它的左视图是（ ） A． B． C． D． 3．一个不透明的口袋中装有 4 个完全相同的小球，把它们分别标号为1， 2 ，3 ， 4 ，随机摸出一个小球 后不放回，再随机摸出一个小球，则两次摸出的小球标号之和等于 6 的概率为（ ） A． 1 6 B． 1 5 C． 1 4 D． 1 3 4．在三角形纸片 ABC 中， 8AB  ， 4BC  ， 6AC  ，按下列方法沿虚线剪下，能使阴影部分的三角 形与 ABC 相似的是（ ） A． B． C． D． 5．在 4 4 的正方形网格中， ABC 和 DEF 的顶点都在边长为1的正方形的顶点上，则图中 ACB 的正 切值为（ ） A． 2 3 B． 1 3 C． 2 2 D．3 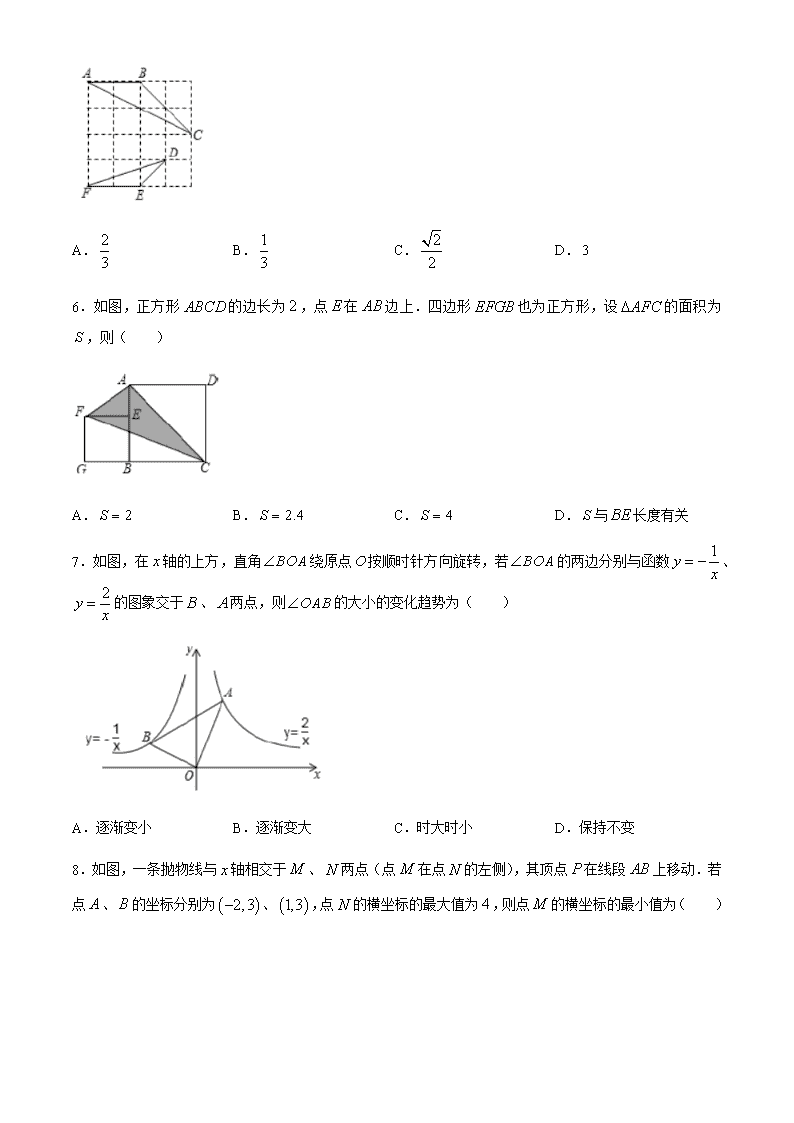6．如图，正方形 ABCD 的边长为 2 ，点 E 在 AB 边上．四边形 EFGB 也为正方形，设 AFC 的面积为 S ， 则（ ） A． 2S  B． 2.4S  C． 4S  D． S 与 BE 长度有关 7．如图，在 x 轴的上方，直角 BOA 绕原点O 按顺时针方向旋转，若 BOA 的两边分别与函数 1y x   、 2y x  的图象交于 B 、 A 两点，则 OAB 的大小的变化趋势为（ ） A．逐渐变小 B．逐渐变大 C．时大时小 D．保持不变 8．如图，一条抛物线与 x 轴相交于 M 、 N 两点（点 M 在点 N 的左侧），其顶点 P 在线段 AB 上移动．若 点 A 、B 的坐标分别为 2,3 、 1,3 ，点 N 的横坐标的最大值为 4 ，则点 M 的横坐标的最小值为（ ） A． 1 B． 3 C． 5 D． 7 二、填空题（本大题共 6 小题，共 18．0 分） 9．已知关于 x 的一元二次方程 2 2( 1) 4 0m x x m m     的一个根为 0 ，则 m 的值是_______． 10．“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古 代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为________尺． 11．2017 年5 月5日我国自主研发的大型飞机 919C 成功首飞，如图给出了一种机翼的示意图，其中 1m  ， 3n  ，则 AB 的长为_______． 12．如图，在 Rt ABC 中， 90C   ， 8AC  ， 6BC  ，点 P 是 AB 上的任意一点，作 PD AC 于 点 D ， PE CB 于点 E ，连结 DE ，则 DE 的最小值为________． 13．如图， A ， B 是反比例函数 4y x  在第一象限内的图象上的两点，且 A ， B 两点的横坐标分别是 2 和 4 ，则 OAB 的面积是________． 14．如图抛物线 2 2 3y x x   与 x 轴交于 A ， B 两点，与 y 轴交于点C ，点 P 是抛物线对称轴上任意一 点，若点 D 、E 、 F 分别是 BC 、 BP 、PC 的中点，连接 DE ， DF ，则 DE DF 的最小值为_______． 三、解答题（本大题共 10 小题，共 78．0 分） 15．计算： 22 cos45 3sin 60 tan 30  16．已知 2 5 0x x   ，求代数式 2( 1) (2 1)x x x   的值． 17．解方程： 23 2 1 0x x   ． 18．如图，在大楼 AB 正前方有一斜坡CD ，坡角 30DCE   ，楼高 60AB  米，在斜坡下的点C 处测 得楼顶 B 的仰角为 60，在斜坡上的 D 处测得楼顶 B 的仰角为 45，其中点 A ，C ， E 在同一直线上． （1）求坡底C 点到大楼距离 AC 的值； （2）求斜坡CD 的长度． 19．如图，在 ABCD 中，BF 平分 ABC 交 AD 于点 F ， AE BF 于点O ，交 BC 于点 E ，连接 EF ． （1）求证：四边形 ABEF 是菱形； （2）连接CF ，若 60ABC   ， 4AB  ， 2AF DF ，求CF 的长． 20．如图，在平面直角坐标系中，正比例函数 y kx 的图象与反比例函数 my x  的图象经过点  2,2A ． （1）分别求这两个函数的表达式； （2）将直线OA 向上平移 3 个单位长度后与 y 轴交于 B ，与反比例函数图象在第一象限内的交点为C ，连 接 AB ， AC ，求点C 的坐标及 ABC 的面积； 21．在一个不透明的盒子中装有大小和形状相同的3 个红球和 2 个白球，把它们充分搅匀． （1）“从中任意抽取1个球不是红球就是白球”是_______事件，“从中任意抽取1个球是黑球”是_______ 事件； （2）从中任意抽取1个球恰好是红球的概率是_______； （3）学校决定在甲、乙两名同学中选取一名作为学生代表发言，制定如下规则： 从盒子中任取两个球，若两球同色，则选甲；若两球异色，则选乙．你认为这个规则公平吗？请用列表法 或画树状图法加以说明． 22．俄罗斯世界杯足球赛期间，某商店销售一批足球纪念册，每本进价 40 元，规定销售单价不低于 44 元， 且获利不高于30% ．试销售期间发现，当销售单价定为 44 元时，每天可售出300 本，销售单价每上涨1元， 每天销售量减少10本，现商店决定提价销售．设每天销售量为 y 本，销售单价为 x 元． （1）请直接写出 y 与 x 之间的函数关系式和自变量 x 的取值范围； （2）当每本足球纪念册销售单价是多少元时，商店每天获利 2400 元？ （3）将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润 w 元最大？最大利润是多少 元？ 23．已知：正方形 ABCD ，等腰直角三角板的直角顶点落在正方形的顶点 D 处，使三角板绕点 D 旋转． 图 1 图 2 （1）当三角板旋转到图 1 的位置时，猜想 CE 与 AF 的数量关系，并加以证明； （2）在（1）的条件下，若 : : 1: 7 :3DE AE CE  ，求 AED 的度数； （3）若 4BC  ，点 M 是边 AB 的中点，连结 DM ，DM 与 AC 交于点O ，当三角板的边 DF 与边 DM 重合时（如图 2），若 5 3OF  ，求 DF 和 DN 的长． 24．抛物线 2y ax bx c   的对称轴为直线 1x  ，该抛物线与 x 轴的两个交点分别为 A 和 B ，与 y 轴的 交点为C ，其中  1,0A  ，  0, 3C  ． （1）写出 B 点的坐标________； （2）若抛物线上存在一点 P ，使得 POC 的面积是 BOC 的面积的 2 倍，求点 P 的坐标； （3）点 M 是线段 BC 上一点，过点 M 作 x 轴的垂线交抛物线于点 D ，求线段 MD 长度的最大值． 参考答案 1．【答案】C 【解析】解： 2 0x x  ，  1 0x x   ， 0x  ， 1 0x   ， 1 0x  ， 2 1x  ， 故选：C． 先分解因式，即可得出两个一元一次方程，求出方程的解即可． 本题考查了解一元二次方程，能把一元二次方程转化成一元一次方程是解此题的关键． 2．【答案】D 【解析】解：从左边看是两个正方形，两正方形的邻边是虚线， 故选：D． 本题考查了简单组合体的三视图，从左边看得到的图形是左视图． 本题考查了简单组合体的三视图，从左边看得到的图形是左视图． 3．【答案】A 【解析】解：画树状图得： 共有12种等可能的结果，两次摸出的小球标号之和等于 6 的有 2 种情况， 两次摸出的小球标号之和等于 6 的概率 2 1 12 6   ． 故选：A． 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的小球标号之和等于 6 的情况， 再利用概率公式求解即可求得答案． 此题考查了列表法或树状图法求概率．当有两个元素时，可用树形图列举，也可以列表列举．解题时注意： 概率  所求情况数与总情况数之比． 4．【答案】D 【解析】解：三角形纸片 ABC 中， 8AB  ， 4BC  ， 6AC  ． A、 4 4 1 8 2AB   ，对应边 6 3 1 8 4 2 AC AB    ，则沿虚线剪下的涂色部分的三角形与 ABC 不相似，故此选 项错误； B、 3 3 8AB  对应边 6 3 3 8 4 8 AC AB    ，则沿虚线剪下的涂色部分的三角形与 ABC 不相似，故此选项错误； C、 2 2 1 6 3AC   ，对应边 6 3 1 8 4 3 AC AB    ，则沿虚线剪下的涂色部分的三角形与 ABC 不相似，故此选 项错误； D、 2 2 1 4 2BC   ，对应边 4 1 1 8 2 2 BC AB    ，则沿虚线剪下的涂色部分的三角形与 ABC 相似，故此选项 正确； 故选：D． 根据相似三角形的判定分别进行判断即可得出答案． 此题主要考查了相似三角形的判定，正确利用相似三角形两边比值相等且夹角相等的两三角形相似是解题 关键． 5．【答案】B 【解析】解：由勾股定理可求出： 2 2BC  ， 2 5AC  ， 10DF  ， 2DE  ， 2 2 FD AC   2 2 FE BC  ， 2 2 ED AB  ， FD ED EF AC AB BC    ， ~FDE CAB  ， DFE ACB   ， 1tan tan 3DFE ACB     ， 故选：B． 根据勾股定理即可求出 AC 、BC 、DE 、DF 的长度，然后证明 FDE ABC  ，推出 ACB DFE   ， 由此即可解决问题． 本题考查解直角三角形，涉及勾股定理，相似三角形的判定与性质，解题的关键是灵活运用相似三角形的 性质解决问题． 6．【答案】A 【解析】解：连接 FB 四边形 EFGB 为正方形 45FBA BAC     ， / /FB AC ABC 与 AFC 是同底等高的三角形 2 ABC ABCDS S  正 ， 2 2 4ABCDS   正 2S  故选：A． 连接 FB ，根据已知可得到 ABC  与 AFC 是同底等高的三角形，由已知可求得 ABC 的面积为大正 方形面积的一半，从而不难求得 S 的值． 本题利用了正方形的性质，内错角相等，两直线平行的判定方法，及同底等高的三角形的面积相等的性质 求解． 7．【答案】D 【解析】解：如图，分别过点 A 、 B 作 AN x 轴、 BM x 轴； 90AOB   ， 90BOM AON AON OAN         ， BOM OAN   ， 90BMO ANO     ， BOM OAN  ， BM OM ON AN   ； 设 1,B m m     ， 2,A n n      ， 则 1BM m  ， 2AN n  ，OM m ，ON n ， 2mn mn   ， 2mn  ； 90AOB   ， tan OBOAB OA    ①； ~BOM OAN  ， 1 2 2 OB BM OA ON mn     ，② 由①②知 2tan 2OAB  为定值， OAB 的大小不变， 故选：D． 如图，作辅助线；首先证明 BOM OAN  ，得到 BM OM ON AN  ；设 1,B m m     ， 2,A n n      ， 得到 1BM m  ， 2AN n  ，OM m ，ON n ，进而得到 2mn mn  ， 2mn  ，此为解决问题的关键 性结论；运用三角函数的定义证明知 2tan 2OAB  为定值，即可解决问题． 该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题；解题的方法 是作辅助线，将分散的条件集中；解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理 或解答． 8．【答案】C 【解析】解：根据题意知， 点 N 的横坐标的最大值为 4 ，此时对称轴过 B 点，点 N 的横坐标最大，此时的 M 点坐标为 2,0 ， 当对称轴过 A 点时，点 M 的横坐标最小，此时的 N 点坐标为  1,0 ， M 点的坐标为 5,0 ， 故点 M 的横坐标的最小值为 5 ， 故选：C． 根据顶点 P 在线段 AB 上移动，又知点 A 、B 的坐标分别为 2,3 、 1,3 ，分别求出对称轴过点 A 和 B 时 的情况，即可判断出 M 点横坐标的最小值． 本题考查了抛物线与 x 轴的交点，二次函数的图象与性质，解答本题的关键是理解二次函数在平行于 x 轴 的直线上移动时，两交点之间的距离不变． 9．【答案】 0 【解析】解：把 0x  代入方程 2 2( 1) 4 0m x x m m     得 2 0m m  ，解得 1 0m  ， 2 1m   ，而 1 0m   ， 所以 0m  ． 故答案为 0 ． 先把 0x  代入方程得到 2 0m m  ，然后解关于 m 的方程，再利用一元二次方程的定义确定满足条件的 m 的值． 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解． 10．【答案】57.5 【解析】解：如图，依题意有 ABF ADE  ， : :AB AD BF DE  ， 即5: 0.4:5AD  ， 解得 62.5AD  ， 62.5 5 57.5BD AD AB      （尺） 故答案为57.5 ． 根据题意可知 ABF ADE  ，根据相似三角形的性质可求 AD ，进一步得到井深． 本题考查了相似三角形的判定与性质，解题的关键是得到 ABF ADE  ． 11．【答案】 2 3 【解析】解：延长 BA 交CE 于点 E ，设 CF BF 于点 F ，如图所示． 在 Rt BDF 中， BF n ， 30DBF   ， 3tan 3DF BF DBF n     ． 在 Rt ACE 中， 90AEC  ， 45ACE   ， AE CE BF n    ， 3 3AB BE AE CD DF AE m n n        ， 1m  ， 3n  ， 2 3AB   ， 故答案为： 2 3 ． 延长 BA 交CE 于点 E ，设 CF BF 于点 F ，通过解直角三角形可求出 DF 、 AE 的长度， 再利用 AB CD DF AE   即可求出结论． 本题考查了解直角三角形的应用，通过解直角三角形求出 DF 、 AE 的长度是解题的关键． 12．【答案】 4.8 【解析】解： Rt ABC 中， 90C   ， 8AC  ， 6BC  ， 10AB  ， 连接CP ， PD AC 于点 D ，  PE CB 于点 E ， 四边形 DPEC 是矩形， DE CP  ， 当 DE 最小时，则CP 最小，根据垂线段最短可知当CP AB 时，则CP 最小， 6 8 4.810DE CP     ． 故答案为： 4.8 ． 连接CP ，根据矩形的性质可知：DE CP ，当 DE 最小时，则CP 最小，根据垂线段最短可知当CP AB 时，则CP 最小，再根据三角形的面积为定值即可求出 CP 的长． 本题考查了勾股定理的运用、矩形的判定和性质以及直角三角形的面积的不同求法，题目难度不大，设计 很新颖，解题的关键是求 DE 的最小值转化为其相等线段 CP 的最小值． 13．【答案】3 【解析】解： A ，B 是反比例函数 4y x  在第一象限内的图象上的两点，且 A ，B 两点的横坐标分别是 2 和 4 ， 当 2x  时， 2y  ，即  2,2A ， 当 4x  时， 1y  ，即  4,1B ． 如图，过 A ， B 两点分别作 AC x 轴于C ， BD x 轴于 D ， 则 1 4 22AOC BODS S     ．  AOB BOD AOC ABDCAODBS S S S S     四边形 梯形 ， AOB ABDCS S  梯形 ，   1 1( ) (1 2) 2 32 2ABDCS BD AC CD       梯形 ， 3AOBS  ． 故答案是：3． 先根据反比例函数图象上点的坐标特征及 A ， B 两点的横坐标，求出  2,2A ，  4,1B ．再 过 A ， B 两点分别作 AC x 轴于 C ， BD x 轴于 D ，根据反比例函数系数 k 的几何意义得出 1 4 22AOC BODS S     ．根据 AOB BOD AOCAODB ABDCS S S S S     四边形 梯形 ，得出 AOB ABDCS S  梯形 ， 利用梯形面积公式求出梯形 1 1( ) (1 2) 2 32 2ABDCS BD AC CD      梯形 ，从而得出 3AOBS  ． 主要考查了反比例函数 ky x  中 k 的几何意义，即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂 线所围成的直角三角形面积 S 的关系即 1 2S k ．也考查了反比例函数图象上点的坐标特征，梯形的面积． 14．【答案】 3 2 2 【解析】解：连接 AC ，交对称轴于点 P ， 则此时 PC PB 最小， 点 D 、 E 、 F 分别是 BC 、 BP 、 PC 的中点， 1 2DE PC  ， 1 2DF PB ， 抛物线 2 2 3y x x   与 x 轴交于 A ， B 两点，与 y 轴交于点C ， 20 2 3x x    解得： 1 3x   ， 2 1x  ， 0x  时， 3y  ， 故 3CO  ， 则 3AO  ，可得： 3 2AC PB PC   ， 故 DE DF 的最小值为： 3 2 2 ． 故答案为： 3 2 2 ． 直接利用轴对称求最短路线的方法得出 P 点位置，再求出 AO ，CO 的长，进而利用勾股定理得出答案． 此题主要考查了抛物线与 x 轴的交点以及利用轴对称求最短路线，正确得出 P 点位置是解题关键． 15．【答案】解：原式 2 2 3 32 32 2 3           3 11 2 3    ， 1 6  ． 【解析】首先代入特殊角的三角函数，然后再进行有理数的加减即可． 本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握 负整数指数幂、零指数幂、二次根式、绝对值等考点的运算． 16．【答案】解：原式 2 22 1 2x x x x     2 1x x    ． 2 5 0x x   ， 2 5x x   ． 原式  2 21 1 5 1 4x x x x             ． 【解析】首先对所求的式子进行化简，把所求的式子化成 2 5x x  的形式，然后代入求解即可． 本题考查了整式的化简求值，正确理解完全平方公式的结构，对所求的式子进行变形是关键． 17．【答案】解：由原方程得： (3 1)( 1) 0x x   ， 可得3 1 0x   或 1 0x   ， 解得： 1 1 3x   ， 2 1x  ． 【解析】方程左边利用十字相乘法分解因式后，利用两数相乘积为 0 两因式中至少有一个为 0 转化为两个 一元一次方程来求解． 此题考查了解一元二次方程—因式分解法，利用此方法解方程时，首先将方程右边化为 0 ，左边化为积的 形式，然后利用两数相乘积为 0 ，两因式中至少有一个为 0 转化为两个一元一次方程来求解． 18．【答案】解：（1）在直角 ABC 中， 90BAC  ， 60BCA   ， 60AB  米， 则 60 20 3tan 60 3 ABAC    （米） 答：坡底C 点到大楼距离 AC 的值是 20 3 米． （2）设 2CD x ，则 DE x ， 3CE x ， 在 Rt BDF 中， 45BDF   ， BF DF  ， 60 20 3 3x x    ， 40 3 60x   ， 2 80 3 120CD x    ， CD 的长为 80 3 120 米． 【解析】（1）在直角三角形 ABC 中，利用锐角三角函数定义求出 AC 的长即可； （2）设 2CD x ，则 DE x ， 3CE x ，构建方程即可解决问题； 此题考查了解直角三角形—仰角俯角问题，坡度坡角问题，熟练掌握勾股定理是解本题的关键． 19．【答案】（1）证明： BF 平分 ABC ， ABF CBF   ． 四边形 ABCD 是平行四边形， / /AD BC ． AFB CBF   ． ABF AFB   ． AB AF  ． AE BF ， BAO FAE   FAE BEO   ． BAO BEO   ． AB BE  ． AF BE  ． 四边形 ABEF 是平行四边形． ABEF 是菱形． （2）解： AD BC ， AF BE ， DF CE  ． 2AF DF 2BE CE  ． 4AB BE  ， 2CE  ． 过点 A 作 AG BC 于点 G ． 60ABC   ， AB BE ， ABE 是等边三角形． 2BG GE   ． 4AF CG   ． 四边形 AGCF 是平行四边形 AGCF 是矩形． AG CF  ． 在 ABG 中， 60ABC   ， 4AB  ， 2 3AG  ． 2 3CF  ． 【解析】（1）由四边形 ABCD 是平行四边形，得到 / /AD BC ，证明 AF 与 BE 平行且相等，可得四边形 ABEF 是平行四边形，再说明 AB AF ，于是得出结论； （2）过点 A 作 AG BC 于点G ，由菱形的性质和等边三角形的性质解答即可本题主要考查了菱形的判定 和性质、勾股定理、平行四边形和矩形的性质和判定，熟练掌握菱形的判定是关键． 20．【答案】解：（1）把  2,2A 代入 y kx 得 2 2k  ， 解得 1k  ； 把  2,2A 代入 my x  得 2 2 4m    ， 正比例函数的解析式为 y x ；反比例函数的解析式为 4y x  ， （2）直线 y x 向上平移 3 的单位得到直线 BC 的解析式为 3y x  ， 当 0x  时， 3 3y x   ，则  0,3B ， 解方程组 4 3 y x y x      得 1 4 x y    或 1 4 x y      点C 的坐标为  1,4 ； 连接OC ， 1 33 12 2ABC OBCS S      ． 【解析】（1）把 A 点坐标分别代入 y kx 和 my x  中分别求出 k 、 m 即可； （2）利用直线平移的规律得到直线 BC 的解析式为 3y x  ，则  0,3B 再解方程组 4 3 y x y x      得点C 的 坐标为 1,4 ；连接OC ，根据三角形面积公式，利用 ABC OBCS S  进行计算． 本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式 联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点． 21．【答案】必然 不可能 3 5 【解析】解：（1）“从中任意抽取1个球不是红球就是白球”是必然事件，“从中任意抽取1个球是黑球”是 不可能事件；故答案为：必然，不可能； （2）从中任意抽取1个球恰好是红球的概率是： 3 5 ； 故答案为： 3 5 （3）如图所示： 由树状图可得：一共有 20 种可能，两球同色的有8 种情况，故选择甲的概率为： 8 2 20 5  ； 则选择乙的概率为： 3 5 ， 故此游戏不公平 （1）直接利用必然事件以及怒不可能事件的定义分别分析得出答案； （2）直接利用概率公式求出答案； （3）首先画出树状图，进而利用概率公式求出答案， 此题主要考查了游戏公平性，正确列出树状图是解题关键． 22．【答案】解：（1） 300 10( 44)y x   ， 即 10 740y x    44 52x  ； （2）根据题意得 ( 40)( 10 740) 2400x x    ， 解得 1 50x  ， 2 64x  （舍去）， 答：当每本足球纪念册销售单价是50元时，商店每天获利 2400 元； （3） ( 40)( 10 740)w x x    210 1140 29600x x    210( 57) 2890x    ， 当 57x  时， w 随 x 的增大而增大， 而 44 52x  ， 所以当 52x  时， w 有最大值，最大值为 210(52 57) 2890 2640    ， 答：将足球纪念册销售单价定为52 元时，商店每天销售纪念册获得的利润 w 元最大，最大利润是 2640 元 【解析】（1）售单价每上涨1元，每天销售量减少10 本，则售单价每上涨  44x  元，每天销售量减少  10 44x  本，所以 300 10( 44)y x   ，然后利用销售单价不低于 44 元，且获利不高于30% 确定 x 的 范围； （2）利用每本的利润乘以销售量得到总利润得到 ( 40)( 10 740) 2400x x    ，然后解方程后利用 x 的范 围确定销售单价； （3）利用利用每本的利润乘以销售量得到总利润得到 ( 40)( 10 740)w x x    ，再把它变形为顶点式， 然后利用二次函数的性质得到 52x  时 w 最大，从而计算出 52x  时对应的 w 的值即可． 本题考查了二次函数的应用：利用二次函数解决利润问题，解此类题的关键是通过题意，确定出二次函数 的解析式，然后利用二次函数的性质确定其最大值；在求二次函数的最值时，一定要注意自变量 x 的取值 范围．也考查了一元二次方程的应用． 23．【答案】解：（1）CE AF ， 在正方形 ABCD 和等腰直角三角形CEF 中， FD DE ，CD CA ， 90ADC EDF    ， ADF CDE   ， ADF CDE   ( )SAS ， CE AF  ； （2）设 DE k ， : : 1: 7 :3DE AE CE  7AE k  ， 3CE AF k  ， 2EF k  ， 2 2 2 2 27 2 9AE EF k k k    ， 2 29AF k ， 即 2 2 2AE EF AF  AEF 为直角三角形， 90BEF   90 45 135AED AEF DEF          ； （3） M 是 AB 的中点， 1 1 2 2MA AB AD   ， / /AB CD ， MAO DCO  ， 1 2 OM OA AM OD OC CD     ， 在 Rt DAM 中， 4AD  ， 2AM  ， 2 5DM  ， 4 5 3DO  5 3OF  ， 45DFN DCO     ， FDN CDO   ， ~DFN DCO  DF DN DC DO   ，即 5 4 4 5 3 DN ， 5 3DN  ． 【解析】（1）由正方形额等腰直角三角形的性质判断出 ADF CDE   即可； （2）设 DE k ，表示出 AE ， CE ， EF ，判断出 AEF 为直角三角形，即可求出 AED ； （3）证 ~MAO DCO  得 1 2 OM OA AM OD OC CD    ，由勾股定理得 2 5DM  ，据此求得 4 5 3DO  ， 结合 5 3OF  知 5DF  ，再证 DFN DCO  得 DF DN DC DO  ，据此计算可得． 此题是四边形的综合问题，主要考查了正方形，等腰直角三角形的性质，全等三角形的性质和判定，相似 三角形的性质和判定，勾股定理及其勾股定理的逆定理，判断 AEF 为直角三角形是解本题的关键，也是 难点． 24．【答案】 3,0 【解析】解：（1）抛物线的对称轴为 1x  ，点 A 坐标为 1,0 ，则点  3,0B ， 故：答案为 3,0 ； （2）二次函数表达式为：  2( 1)( 3) 2 3y a x x a x x      ， 即： 3 3a   ，解得： 1a  ， 故抛物线的表达式为： 2 2 3y x x   ， 由题意得： 2POC BOCS S  ，则 2 6x OB   ， 故点 P 的坐标为 6,21 或 6,45 ； （3）如图所示， 将点 B 、C 坐标代入一次函数 y kx b  得表达式得： 3 3 0 c k b      ，解得： 1 3 k b     ， 故直线 BC 的表达式为： 3y x  ， 设：点 M 坐标为 , 3x x  ，则点 D 坐标为 2, 2 3x x x  ， 则 2 2 3 93 2 3 2 4MD x x x x            ， 故 MD 长度的最大值为 9 4 ． （1）抛物线的对称轴为 1x  ，点 A 坐标为 1,0 ，则点  3,0B ，即可求解； （2）由 2POC BOCS S  ，则 2 6x OB   ，即可求解； （3）设：点 M 坐标为 , 3x x  ，则点 D 坐标为 2, 2 3x x x  ，则 23 2 3MD x x x     ，即可求解． 主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代 数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系． 九年级数学上学期期末检测试题（二） 一、选择题（本大题共 12 小题，共 48.0 分） 1.如图，在 Rt ABC 中， 90ACB  ，如果 3AC  ， 5AB  ，那么sin B 等于（ ） A. 3 5 B. 4 5 C. 3 4 D. 4 3 2.如图所示的几何体为圆台，其俯视图正确的是（ ） A. B. C. D. 3.二次函数  22 1 3y x    的图象的顶点坐标是（ ） A. 1,3 B. 1,3 C. 1, 3 D. 1, 3  4.如图，已知 ADE ABC ∽ ，且 : 2:1AD DB  ，则 :ADE ABCS S   （ ） A. 2:1 B. 4:1 C. 2:3 D. 4:9 5.已知一元二次方程 2 5 0x kx   有一个根为 1， k 的值为（ ） A. 2 B.2 C. 4 D.4 6.一个不透明的口袋中放着若干个红球和白球，这两种球除了颜色以外没有任何其他区别，袋中的球已经 搅匀，从口袋中随机取出一个球，取出红球的概率是 1 4 .如果袋中共有 32 个小球，那么袋中的红球有（ ） A.4 个 B.6 个 C.8 个 D.10 个 7.反比例函数 ky x  图象经过  1,2A ，  , 2B n  两点，则 n （ ） A.1 B.3 C. 1 D. 3 8.如图，平行四边形 ABCD 中， AC AB ，点 E 为 BC 边中点， 6AD  ，则 AE 的长为（ ） A.2 B.3 C.4 D.5 9.如图， AB 是 O 的直径，点C 、 D 在 O 上.若 130BOD   ，则 ACD 的度数为（ ） A.50 B.30 C. 25 D. 20 10.如图，甲、乙为两座建筑物，它们之间的水平距离 BC 为30m，在 A 点测得 D 点的仰角 EAD 为 45， 在 B 点测得 D 点的仰角 CBD 为 60，则乙建筑物的高度为（ ）米. A.30 3 B.30 3 30 C.30 D.30 2 11.如图，已知直线 2 5y x   与 x 轴交于点 A ，与 y 轴交于点 B ，将 AOB 沿直线 AB 翻折后，设点O 的对应点为点C ，双曲线  0ky xx   经过点C ，则 k 的值为（ ） A.8 B.6 C. 4 3 D. 4 5 12.如图，在菱形 ABCD 中， 60B   ， 6BC  ， E 为 BC 中点， F 是 AB 上一点， G 为 AD 上一点， 且 2BF  ， 60FEG  ， EG 交 AC 于点 H ，关于下列结论，正确序号的选项是（ ） ① BEF CHE ∽ ，② 1AG  ，③ 3 72EH  ④ 3BEF AGHS S  A.①② B.①②③ C.①②④ D.①③④ 二、填空题（本大题共 6 小题，共 24.0 分） 13.如图，任意转动正六边形转盘一次，当转盘停止转动时，指针指向大于 3 的数的概率是_________. 14.某数学兴趣小组利用太阳光测量一棵树的高度（如图），在同一时刻，测得树的影长为 6 米，小明的影 长为 1 米，已知小明的身高为 1.5 米，则树高为_________米. 15.已知抛物线 2y x bx c   经过点  0,5A 、  4,5B ，那么此抛物线的对称轴是___________. 16.如图， O 的半径为 6cm ，直线 AB 是 O 的切线，切点为点 B ，弦 AB AO ，若 30A  ，则劣 弧 BC 的长为________ cm . 17.已知二次函数  2 0y ax bx c a    的图象如图所示，下列结论：① 0abc  ；② 2 0a b  ；③ 2 4 0b ac  ；④ 0a b c   ，其中正确的是_________.（把所有正确结论的序号都填在横线上） 18.如图，是将菱形 ABCD 以点 O 为中心按顺时针方向分别旋转 90 ，180 ， 270 后形成的图形.若 60BAD   ， 2AB  ，则图中阴影部分的面积为_________. 三、计算题（本大题共 2 小题，共 16.0 分） 19.解方程： 2 4 5 0x x   . 20.某工厂设计了一款成本为 20 元/件的工艺品投放市场进行试销，经过调查，得到如下数据： 销售单价 x （元/件） … 30 40 50 60 … 每天销售量 y （件） … 500 400 300 200 … （1）研究发现，每天销售量 y 与单价 x 满足一次函数关系，求出 y 与 x 的关系式； （2）当地物价部门规定，该工艺品销售单价最高不能超过 45 元/件，那么销售单价定为多少时，工艺厂试 销该工艺品每天获得的利润 8000 元？ 四、解答题（本大题共 5 小题，共 38.0 分） 21.计算： 1 02 12 4sin 60 ( 2019)     . 22.已知：如图，在 ABCD 中， ,E F 是对角线 BD 上两个点，且 BE DF .求证： AE CF . 23.为了了解全校 1500 名学生对学校设置的篮球、羽毛球、乒乓球、踢键子、跳绳共 5 项体育活动的喜爱 情况，在全校范围内随机抽查部分学生，对他们喜爱的体育项目（每人只选一项）进行了问卷调查，将统 计数据绘制成如图两幅不完整统计图，请根据图中提供的信息解答下列各题. （1） m  ____________ % ，这次共抽取了_______名学生进行调查；并补全条形图； （2）请你估计该校约有__________名学生喜爱打篮球； （3）现学校准备从喜欢跳绳活动的 4 人（三男一女）中随机选取 2 人进行体能测试，请利用列表或画树状 图的方法，求抽到一男一女学生的概率是多少？ 24.如图， AB 是 O 的直径，点 D 在 AB 的延长线上， AC 平分 DAE 交 O 于点C ，且 AE DC 的 延长线，垂足为点 E . （1）求证：直线CD 是 O 的切线； （2）若 6AB  ， 2BD  ，求CE 的长. 25.如图，直线 2 2y x  与 y 轴交于 A 点，与反比例函数  0ky xx   的图象交于点 M ，过 M 作 MH x 轴于点 H ，且 tan 2AHO  . （1）求 H 点的坐标及 k 的值； （2）点 P 在 y 轴上，使 AMP 是以 AM 为腰的等腰三角形，请直接写出所有满足条件的 P 点坐标； （3）点  ,1N a 是反比例函数  0ky x x  图象上的点，点  ,0Q m 是 x 轴上的动点，当 MNQ 的面积 为 3 时，请求出所有满足条件的 m 的值. 答案和解析 1.【答案】A 【解析】解：在 Rt ABC 中， 90ACB  ， 3AC  ， 5AB  ，∴ 3sin 5 ACB AB   .故选 A. 直接利用锐角三角函数关系得出sin B 的值. 此题主要考查了锐角三角函数关系.正确把握定义是解题关键. 2.【答案】C 【解析】解：从几何体的上面看所得到的图形是两个同心圆，故选：C. 俯视图是从物体上面看，所得到的图形. 本题考查了几何体的三种视图，掌握定义是关键.注意所有的看到的棱都应表现在三视图中. 3.【答案】B 【解析】解：∵  22 1 3y x    ，∴抛物线顶点坐标为 1,3 ，故选：B. 由抛物线的解析式可求得答案. 本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在  2y a x h k   中，对称轴 为 x h ，顶点坐标为  ,h k . 4.【答案】D 【解析】解：∵ : 2:3AD DB  ，∴ : 2:3AD AB  ， ∵ ADE ABC ∽ ，∴ 2 4 9 ADE ABC S AD S AB        ，故选：D. 根据相似三角形的面积比等于相似比的平方即可解决问题. 本题考查相似三角形的性质，解题的关键是熟练掌握相似三角形的性质解决问题，记住相似三角形的面积 比等于相似比的平方. 5.【答案】D 【解析】解：把 1x  代入方程得1 5 0k   ，解得 4k  .故选：D. 根据一元二次方程的解的定义，把 1x  代入方程得关于 k 的一次方程1 5 0k   ，然后解一次方程即可. 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解. 6.【答案】C 【解析】解：设袋中的红球有 x 个，根据题意得： 1 32 4 x  ，解得： 8x  ，故选：C. 根据概率的求法，找准两点： 1、符合条件的情况数目； 2、全部情况的总数；二者的比值就是其发生的概率. 此题考查概率的求法：如果一个事件有 n 种可能，而且这些事件的可能性相同， 其中事件 A 出现 m 种结果，那么事件 A 的概率   mP A n  . 7.【答案】C 【解析】解：∵反比例函数 ky x  图象经过  1,2A ，  , 2B n  两点， ∴ 1 2 2k n    .解得 1n   .故选：C. 根据反比例函数图象上点的坐标特征得到： 1 2 2k n    . 考查了反比例函数图象上点的坐标特征.图象上的点  ,x y 的横纵坐标的积是定值 k ，即 xy k . 8.【答案】B 【解析】解：∵四边形 ABCD 是平行四边形，∴ 6BC AD  ， ∵ E 为 BC 的中点， AC AB ，∴ 1 32AE BC  ，故选：B. 由平行四边形的性质得出 6BC AD  ，由直角三角形斜边上的中线性质即可得出结果. 本题主要考查了平行四边形的性质和直角三角形斜边上的中线性质，熟练掌握平行四边形的性质并由直角 三角形斜边上的中线性质求出 AE 是解决问题的关键. 9.【答案】C 【解析】解：∵ 130BOD  ，∴ 50AOD   ， ∴ 1 252ACD AOD     ，故选：C. 根据圆周角定理计算即可. 本题考查圆周角定理，解题的关键是熟练掌握基本知识，属于中考常考题型. 10.【答案】B 【解析】解：如图，过 A 作 AF CD 于点 F . 在 Rt BCD 中， 60DBC   ， 30BC m ， ∵ tan CDDBC BC   ，∴ tan 60 30 3CD BC m   ， ∴甲建筑物的高度为 30 3m ； 在 Rt AFD 中， 45DAF   ，∴ 30DF AF BC m   ， ∴ (30 3 30)AB CF CD DF m     ， ∴乙建筑物的高度为 (30 3 30)m . 故选：B. 在 Rt BCD 中可求得CD 的长，即求得甲的高度，过 A 作 AF CD 于点 F ，在 Rt ADF 中可求得 DF ， 则可求得 CF 的长，即可求得乙的高度. 本题主要考查角直角三角形的应用-仰角俯角问题，构造直角三角形，利用特殊角求得相应线段的长是解题 的关键. 11.【答案】A 【解析】解：作CD y 轴于 D ，CE x 轴于 E ，如图，设  ,C a b ， 当 0x  时， 2 5 5y x    ，则  0,5B ， 当 0y  时， 2 5 0x   ，解得 5 2x  ，则 5 ,02A     ， ∵ AOB 沿直线 AB 翻折后，点O 的对应点为点C ， ∴ 5BC BO  ， 5 2AC AO  ， 在 Rt BCD 中，  22 25 5a b   ，① 在 Rt ACE 中， 2 2 25 5 2 2a b            ，② ①-②得 2a b ，把 2a b 代入①得 2 2 0b b  ，解得 2b  ， ∴ 4a  ，∴  4,2C ，∴ 4 2 8k    .故选 A. 作CD y 轴于 D ，CE x 轴于 E ，设  ,C a b .依据直线的解析式即可得到点 A 和点 B 的坐标，进而得 出 5BC BO  ， 5 2AC AO  ，再根据勾股定理即可得到 2a b ，进而得出  4,2C ，即可得到 k 的值. 本题考查了反比例函数图象上点的坐标特征：反比例函数 ky x  （ k 为常数， 0k  ）的图象是双曲线，图 象上的点 ,x y 的横纵坐标的积是定值 k ，即 xy k . 12.【答案】B 【解析】解：∵菱形 ABCD 中， 60B   ， 60FEG   . ∴ 60B ECH     ， 120BEF CHE CEH    ， ∴ BEF CHE ∽ ，故①正确；∴ BF BE CE CH  ， 又∵ 6BC  ， E 为 BC 中点， 2BF  ， ∴ 2 3 3 CH  ，即 4.5CH  ， 又∵ 6AC BC  ，∴ 1.5AH  ∵ AG CE ，∴ AGH CEH ∽ ，∴ AG AH CE CH  ， ∴ 1 13AG CE  ，故②正确； 如图，过 F 作 FP BC 于 P ， 则 30BFP  ，∴ 1 12BP BF  ， 3 1 2PE    ， 3PF  ， ∴ Rt EFP 中， 2 2 7EF EP PE   ， 又∵ 2 3 EF BF HE CE   ，∴ 3 3 7 2 2EH EF  ，故③正确； ∵ 1 3AG CE ， 2 3BF CE ， BEF CHE ∽ ， AGH CEH ∽ ， ∴ 9CEH AGHS S  ， 9 4CEH BEFS S  ，∴ 99 4AGH BEFS S  ， ∴ 4BEF AGHS S  ，故④错误；故选：B. 依据 60B ECH     ， BEF CHE  ，即可得到 BEF CHE ∽ ； 依据 AGH CEH ∽ ，即可得出 1 13AG CE  ； 过 F 作 FP BC 于 P ，依据 7EF  ，根据相似三角形的性质得到 EH ； 依据 9CEH AGHS S  ， 9 4CEH BEFS S  ， 可得 99 4AGH BEFS S  ，进而得到 4BEF AGHS S  . 此题考查了相似三角形的判定与性质、菱形的性质、等边三角形的性质的综合运用.在判定两个三角形相似 时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用. 13.【答案】 1 2 【解析】解：∵共 6 个数，大于 3 的数有 3 个， ∴ P （大于 3） 3 1 6 2   ；故答案为 1 2 . 根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率. 本题考查概率的求法：如果一个事件有 n 种可能，而且这些事件的可能性相同，其中事件 A 出现 m 种结果， 那么事件 A 的概率   mP A n  . 14.【答案】9 【解析】解：根据相同时刻的物高与影长成比例.设树的高度为 xm， 则 1 6 1.5 x  ，解得： 9x  .故答案为：9. 在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，对应比值相等进而得出答案. 本题主要考查了同一时刻物高和影长成正比，考查利用所学知识解决实际问题的能力. 15.【答案】直线 2x  【解析】解：∵点  0,5A 、  4,5B 的纵坐标都是 5 相同， ∴抛物线的对称轴为直线 0 4 22x   . 故答案为：直线 2x  . 根据点 A 、 B 的纵坐标相等判断出 A 、 B 关于对称轴对称，然后列式计算即可得解. 本题考查了二次函数的性质，观察出 A 、 B 是对称点是解题的关键. 16.【答案】 2 【解析】解：∵直线 AB 是 O 的切线，∴OB AB ， 又∵ 30A  ，∴ 60BOA  ， ∵弦 BC AO ，OB OC ，∴ OBC 是等边三角形. 即可得 60BOC   ，∴劣弧 BC 的长 60 2180 R cm   . 故答案为： 2 . 根据切线的性质可得出 OB AB ，继而求出 BOA 的度数，利用弦 BC AO ，及 OB OC 可得出 BOC 的度数，代入弧长公式即可得出答案. 此题考查了弧长的计算公式、切线的性质，根据切线的性质及圆的性质得出 OBC 是等边三角形是解答本 题的关键.另外要熟练记忆弧长的计算公式. 17.【答案】①②③ 【解析】解：开口向上的 0a  ，与 y 轴的交点得出 0c  ， 0 12 b a    ， 0b  ， 0abc  ，①对 12 b a   ， 0a  ， 2b a  ， 2 0a b  ，②对 抛物线与 x 轴有两个交点， 2 4 0b ac  ，③对 从图可以看出当 1x   时，对应的 y 值大于 0， 0a b c   ，④错 故答案：①②③ 由图形先得到 , ,a b c 和 2 4b ac 正负性，再来观察对称轴和 1x   时 y 的值，综合得出答案 本题考查了二次函数的系数和抛物线图象的关系，一般这类题从图中基本可以读出 , ,a b c 和 2 4b ac 正负 性，再根据 2 b a  ， a b c  ， a b c  等条件合理放缩等到题干中的一些结论 18.【答案】12 4 3 【解析】解：如图所示，连接 AC ， BD 交于点 E ，连接 DF ， FM ， MN ， DN ， ∵将菱形 ABCD 以点O 为中心按顺时针方向分别旋转90 ，180， 270后形成的图形， 60BAD   ， 2AB  ，∴ AC BD ，四边形 DNMF 是正方形， 90AOC   ， 2BD  ， 3AE EC  . ∴ 45AOE  ， 1ED  ，∴ 3AE EO  ， 3 1DO   ， ∴ DNMFS正方形 12( 3 1) 2( 3 1) 8 4 32        ， 1 sin30 12ADFS AD AF       ， 则图中阴影部分的面积为： 4 4 8 4 3 12 4 3ADF DNMFS S      正方形 . 故答案为：12 4 3 . 根据菱形的性质得出 DO 的长，进而求出 DNMFS正方形 ，进而得出 ADFS 即可得出答案. 此题主要考查了菱形的性质以及旋转的性质，得出正确分割图形得出 DO 的长是解题关键. 19.【答案】解：原方程变形为  1 5 0x x   ∴ 1 5x   ， 2 1x  . 【解析】通过观察方程形式，利用二次三项式的因式分解法解方程比较简单. 本题考查了因式分解法解一元二次方程，当把方程通过移项把等式的右边化为 0 后方程的左边能因式分解 时，一般情况下是把左边的式子因式分解，再利用积为 0 的特点解出方程的根.因式分解法是解一元二次方 程的一种简便方法，要会灵活运用. 20.【答案】解：（1）设 y kx b  ，根据题意可得 30 500 40 400 k b k b      ， 解得： 10 800 k b     ，则 10 800y x   ； （2）根据题意，得：  20 10 800 8000x x    ， 整理，得： 2 100 2400 0x x   ，解得： 1 40x  ， 2 60x  ， ∵销售单价最高不能超过 45 元/件，∴ 40x  ， 答：销售单价定为 40 元/件时，工艺厂试销该工艺品每天获得的利润 8000 元. 【解析】 （1）利用待定系数法求解可得； （2）根据“总利润 单件利润 销售量”可得关于 x 的一元二次方程，解之即可得. 本题主要考查一元二次方程的应用.解题的关键是熟练掌握待定系数法求函数解析式及找到题目蕴含的相 等关系. 21.【答案】解：原式 1 3 1 12 3 4 1 2 3 2 3 12 2 2 2            . 【解析】直接利用负指数幂的性质以及特殊角的三角函数值以及零指数幂的性质分别化简得出答案. 此题主要考查了实数运算，正确化简各数是解题关键. 22.【答案】证明：∵四边形 ABCD 为平行四边形， ∴ AB DC ， AB DC ，∴ ABE CDF   ， 又∵ BE DF ，在 ABE 与 CDF 中 AB DC ABE CDF BE DF       ， ∴  ABE CDF SAS ≌ ∴ AE CF . 【解析】根据平行四边形的性质和全等三角形的判定和性质证明即可. 此题考查平行四边形的性质，关键是根据平行四边形的性质和全等三角形的判定和性质解答. 23.【答案】20 50 360 【解析】解：（1） 100% 14% 8% 24% 34% 20%m       ； ∵跳绳的人数有 4 人，占的百分比为8%， ∴ 4 8% 50  ；故答案为：20，50； 如图所示：50 20% 10  （人）. （2）1500 24% 360  ；故答案为：360 （3）列表如下： 男 1 男 2 男 3 女 男 1 男 2，男 1 男 3，男 1 女，男 1 男 2 男 1，男 2 男 3，男 2 女，男 2 男 3 男 1，男 3 男 2，男 3 女，男 3 女 男 1，女 男 2，女 男 3，女 ∵所有可能出现的结果共 12 种情况，并且每种情况出现的可能性相等.其中一男一女的情况有 6 种. ∴抽到一男一女的概率 6 1 12 2P   . （1）首先由条形图与扇形图可求得 100% 14% 8% 24% 34% 20%m       ；由跳绳的人数有 4 人， 占的百分比为8%，可得总人数 4 8% 50  ； （2）由1500 24% 360  ，即可求得该校约有 360 名学生喜爱打篮球； （3）首先根据题意画出表格，然后由表格即可求得所有等可能的结果与抽到一男一女学生的情况，再利用 概率公式即可求得答案. 本题考查的是用列表法或画树状图法求概率以及扇形统计图、条形统计图的知识.注意列表法或画树状图法 可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上 完成的事件.用到的知识点为：概率 所求情况数与总情况数之比. 24.【答案】证明：（1）连接 OC ∵OA OC ，∴ OAC OCA   ， ∵ EAC OAC   ，∴ EAC ACO   ，∴ AE OC ， ∵ 90AEC  ∴ OCD AEC   ，∴ 90OCD   ， ∴CD 是 O 的切线 （2）∵ 6AB  ， 2BD  ∴ 3OC OA OB   ， 5OD  又∵ 90OCD   ，∴ 2 2 4CD OD OC   ∵ AE OC ，∴ CD OD DE AD  ∴ 4 5 8DE  ∴ 32 5DE  ∴ 12 5CE DE CD   【解析】 （1）连接OC ，由角平分线的性质和等腰三角形的性质可得 DAC EAC   ，可得 AE OC ，由平行 线的性质可得 90OCD   ，可得结论； （2）本题考查了切线的判定和性质，等腰三角形的性质，平行线分线段成比例等知识，熟练运用切线的判 定和性质是本题的关键. 25.【答案】解：（1）由 2 2y x  可知  0,2A ，即 2OA  ， ∵ tan 2AHO  ，∴ 1OH  ，∴  1,0H ， ∵ MH x 轴，∴点 M 的横坐标为 1， ∵点 M 在直线 2 2y x  上， ∵点 M 的纵坐标为 4，即  1,4M ， ∵点 M 在 ky x  上，∴ 1 4 4k    （2）①当 AM AP 时，∵  0,2A ，  1,4M ， ∴ 5AM  ，则 5AP AM  ， ∴此时点 P 的坐标为 0,2 5 或 0,2 5 ； ②若 AM PM 时，设  0,P y ，则 2 2(1 0) (4 )PM y    ， ∴ 2 2(1 0) (4 ) 5y    ，解得 2y  （舍）或 6y  ， 此时点 P 的坐标为  0,6 ， 综上所述，点 P 的坐标为 0,6 或 0,2 5 ，或 0,2 5 ； （3）∵点  ,1N a 在反比例函数  4 0y x x  图象上， ∴ 4a  ，∴点  4,1N ， 延长 MN 交 x 轴于点C ， 设直线 MN 的解析式为 y mx n  ， 则有 4 4 1 m n m n      ，解得 1 5 m n     ， ∵直线 MN 的解析式为 5y x   . ∵点C 是直线 5y x   与 x 轴的交点， ∴点C 的坐标为 5,0 ， 5OC  ，∵ 3MNQS  ， ∴ 1 1 34 1 32 2 2MNQ MQC NQCS S S QC QC QC           ， ∴ 2QC  ，∵  5,0C ，  ,0Q m ， ∴| 5| 2m   ，∴ 7m  或 3， 故答案为：7 或 3. 【解析】 （1）先求出 2OA  ，结合 tan 2AHO  可得OH 的长，即可得知点 M 的横坐标，代入直线解析式可得 点 M 坐标，代入反比例解析式可得 k 的值； （2）分 AM AP 和 AM PM 两种情况分别求解可得； （3）先求出点  4,1N ，延长 MN 交 x 轴于点C ，待定系数法求出直线 MN 解析式为 5y x   .据此求 得 5OC  ，再由 3MNQ MQC NQCS S S    知 2QC  ，再进一步求解可得. 本题是反比例函数综合问题，解题的关键是掌握待定系数法求一次函数和反比例函数解析式、等腰三角形 的判定与性质、两点之间的距离公式及三角形的面 九年级数学上学期期末检测试题（三） 一．选择题（共 10 小题） 1．下列图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 2．下列方程是一元二次方程的是（ ） A．x（x﹣1）＝x2 B．x2＝0 C．x2﹣2y＝1 D． 3．二次函数 y＝（x﹣4）2+2 图象的顶点坐标是（ ） A．（﹣4，2） B．（4，﹣2） C．（4，2） D．（﹣4，﹣2） 4．关于 x 的一元二次方程 x2﹣2x﹣m＝0 有实根，则 m 的值可能是（ ） A．﹣4 B．﹣3 C．﹣2 D．﹣1 5．如图，在 ⊙ O，点 A、B、C 在 ⊙ O 上，若∠OAB＝54°，则∠C（ ） A．54° B．27° C．36° D．46° 6．一个布袋里装有 2 个红球、3 个黄球和 5 个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是黄 球的概率为（ ） A． B． C． D． 7．天虹商场一月份鞋帽专柜的营业额为 100 万元，三月份鞋帽专柜的营业额为 150 万元．设一到三月每月 平均增长率为 x，则下列方程正确的是（ ） A．100（1+2x）＝150 B．100（1+x）2＝150 C．100（1+x）+100（1+x）2＝150 D．100+100（1+x）+100（1+x）2＝150 8．如图，在同一平面直角坐标系中，一次函数 y1＝kx+b（k、b 是常数，且 k≠0）与反比例函数 y2＝ （c 是常数，且 c≠0）的图象相交于 A（﹣3，﹣2），B（2，m）两点，则不等式 y1＞y2 的解集是（ ） A．﹣3＜x＜2 B．x＜﹣3 或 x＞2 C．﹣3＜x＜0 或 x＞2 D．0＜x＜2 9．如图是二次函数 y＝ax2+bx+c 图象的一部分，其对称轴是 x＝﹣1，且过点（﹣3，0），说法： ① abc＜0； ② 2a﹣b＝0； ③ ﹣a+c＜0； ④ 若（﹣5，y1）、（ ，y2）是抛物线上两点，则 y1＞y2，其中说法正确的有 （ ）个． A．1 B．2 C．3 D．4 10．在平面直角坐标系中，若干个半径为 1 的单位长度，圆心角为 60°的扇形组成一条连续的曲线，点 P 从原点 O 出发，向右沿这条曲线做上下起伏运动（如图），点 P 在直线上运动的速度为每 1 个单位长度．点 P 在弧线上运动的速度为每秒 个单位长度，则 2019 秒时，点 P 的坐标是（ ） A．（ ， ） B．（ ，﹣ ） C．（2019， ） D．（2019，﹣ ） 二．填空题（共 5 小题） 11．方程 x2＝﹣4x 的解是 ． 12．如图，将△ABC 绕点 A 逆时针旋转 140°，得到△ADE，这时点 B，C，D 恰好在同一直线上，则∠B 的度数为 ． 13．如图，点 B 是双曲线 y＝ （k≠0）上的一点，点 A 在 x 轴上，且 AB＝2，OB⊥AB，若∠BAO＝60°， 则 k＝ ． 14．如图，在边长为 2 的正方形 ABCD 中，以点 D 为圆心，AD 长为半径画 ，再以 BC 为直径画半圆， 若阴影部分 ① 的面积为 S1，阴影部分 ② 的面积为 S2，则图中 S1﹣S2 的值为 ．（结果保留 π ） 15．如图，在▱ ABCD 中，AB＝6，BC＝6 ，∠D＝30°，点 E 是 AB 边的中点，点 F 是 BC 边上一动点， 将△BEF 移沿直线 EF 折叠，得到△GEF，当 FG∥AC 时，BF 的长为 ． 三．解答题（共 8 小题） 16．解下列方程： （1）x2﹣2x﹣2＝0； （2）（x﹣1）（x﹣3）＝8． 17．如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别是 A（﹣4，1），B（﹣1，2），C（﹣2， 4） （1）将△ABC 向右平移 4 个单位后得到△A1B1C1，请画出△A1B1C1，并写出点 B1 的坐标； （2）△A2B2C2 和△A1B1C1 关于原点 O 中心对称，请画出△A2B2C2，并写出点 C2 的坐标； （3）连接点 A 和点 B2，点 B 和点 A2，得到四边形 AB2A2B，试判断四边形 AB2A2B 的形状（无须说明理 由）． 18．图 ① 是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字 2，3，4，5．图 ② 是一个正六边 形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子在桌面掷出后，看骰子落在桌面上（即 底面）的数字是几，就从图中的 A 点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处 开始，按第一次的方法继续…… （1）随机掷一次骰子，则棋子跳动到点 C 处的概率是 ． （2）随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点 C 处的概率． 19．如图，AB 是 ⊙ O 的直径，BM 切 ⊙ O 于点 B，点 P 是 ⊙ O 上的一个动点（点 P 不与 A，B 两点重合）， 连接 AP，过点 O 作 OQ∥AP 交 BM 于点 Q，过点 P 作 PE⊥AB 于点 C，交 QO 的延长线于点 E，连接 PQ，OP． （1）求证：△BOQ≌△POQ； （2）若直径 AB 的长为 12． ① 当 PE＝ 时，四边形 BOPQ 为正方形； ② 当 PE＝ 时，四边形 AEOP 为菱形． 20．参照学习函数的过程与方法，探究函数 y＝ （x≠0）的图象与性质，因为 y＝ ，即 y＝ ﹣ +1，所以我们对比函数 y＝﹣ 来探究． 列表： x … ﹣4 ﹣3 ﹣2 ﹣1 ﹣ 1 2 3 4 … y＝﹣ … 1 2 4 ﹣4 ﹣2 ﹣1 ﹣ ﹣ … y＝ … 2 3 5 ﹣3 ﹣1 0 … 描点：在平面直角坐标系中以自变量 x 的取值为横坐标，以 y＝ 相应的函数值为纵坐标，描出相应 的点如图所示； （1）请把 y 轴左边点和右边各点分别用一条光滑曲线，顺次连接起来； （2）观察图象并分析表格，回答下列问题： ① 当 x＜0 时，y 随 x 的增大而 ；（“增大”或“减小”） ② y＝ 的图象是由 y＝﹣ 的图象向 平移 个单位而得到的： ③ 图象关于点 中心对称．（填点的坐标） （3）函数 y＝ 与直线 y＝﹣2x+1 交于点 A，B，求△AOB 的面积． 21．某水果商场经销一种高档水果，原价每千克 50 元，连续两次降价后每千克 32 元，若每每次下降的百 分率相同 （1）求每次下降的百分率； （2）若每千克盈利 10 元，每天可售出 500 千克，经市场调查发现，在进货价不变的情况下，商场决定 采取适当的涨价措施，若每千克涨价 1 元，日销售量将减少 20 千克，现该商场要保证每天盈利 6000 元， 且要尽快减少库存，那么每千克应涨价多少元？ 22．在 Rt△ABC 中，∠BCA＝90°，∠A＜∠ABC，D 是 AC 边上一点，且 DA＝DB，O 是 AB 的中点，CE 是△BCD 的中线． （1）如图 a，连接 OC，请直接写出∠OCE 和∠OAC 的数量关系： ； （2）点 M 是射线 EC 上的一个动点，将射线 OM 绕点 O 逆时针旋转得射线 ON，使∠MON＝∠ADB， ON 与射线 CA 交于点 N． ① 如图 b，猜想并证明线段 OM 和线段 ON 之间的数量关系； ② 若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段 ME 的长度（用含 m 的代数式表示）． 23．如图，若 b 是正数．直线 l：y＝b 与 y 轴交于点 A，直线 a：y＝x﹣b 与 y 轴交于点 B；抛物线 L：y＝ ﹣x2+bx 的顶点为 C，且 L 与 x 轴右交点为 D． （1）若 AB＝6，求 b 的值，并求此时 L 的对称轴与 a 的交点坐标； （2）当点 C 在 l 下方时，求点 C 与 l 距离的最大值； （3）设 x0≠0，点（x0，y1），（x0，y2），（x0，y3）分别在 l，a 和 L 上，且 y3 是 y1，y2 的平均数，求点（x0， 0）与点 D 间的距离； （4）在 L 和 a 所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出 b ＝2019 和 b＝2019.5 时“美点”的个数． 参考答案与试题解析 一．选择题（共 10 小题） 1．下列图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 【分析】根据中心对称图形和轴对称图形的概念对各选项分析判断即可得解． 【解答】解：A、是轴对称图形，也是中心对称图形，故本选项符合题意； B、不是轴对称图形，不是中心对称图形，故本选项不合题意； C、是轴对称图形，不是中心对称图形，故本选项不合题意； D、是轴对称图形，不是中心对称图形，故本选项不合题意． 故选：A． 2．下列方程是一元二次方程的是（ ） A．x（x﹣1）＝x2 B．x2＝0 C．x2﹣2y＝1 D． 【分析】根据一元二次方程的定义解答．一元二次方程必须满足四个条件：未知数的最高次数是 2；二 次项系数不为 0；是整式方程；含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件 者为正确答案． 【解答】解：A、由已知方程得到：﹣x＝0，不是一元二次方程，故本选项不符合题意． B、该方程符合一元二次方程的定义，故本选项符合题意． C、该方程中含有两个未知数，属于二元二次方程，故本选项不符合题意． D、该方程不是整式方程，故本选项不符合题意． 故选：B． 3．二次函数 y＝（x﹣4）2+2 图象的顶点坐标是（ ） A．（﹣4，2） B．（4，﹣2） C．（4，2） D．（﹣4，﹣2） 【分析】利用顶点式方程可直接得到抛物线的顶点坐标． 【解答】解：∵y＝（x﹣4）2+2， ∴顶点坐标为（4，2）， 故选：C． 4．关于 x 的一元二次方程 x2﹣2x﹣m＝0 有实根，则 m 的值可能是（ ） A．﹣4 B．﹣3 C．﹣2 D．﹣1 【分析】根据方程的系数结合根的判别式△≥0，即可得出关于 m 的一元一次不等式，解之即可得出 m 的取值范围，从而求解． 【解答】解：∵关于 x 的一元二次方程 x2﹣2x﹣m＝0 有实根， ∴△＝（﹣2）2﹣4×1×（﹣m）≥0， 解得：m≥﹣1． 故选：D． 5．如图，在 ⊙ O，点 A、B、C 在 ⊙ O 上，若∠OAB＝54°，则∠C（ ） A．54° B．27° C．36° D．46° 【分析】先利用等腰三角形的性质和三角形内角和计算出∠AOB 的度数，然后利用圆周角定理得到∠C 的度数． 【解答】解：∵OA＝OB， ∴∠OBA＝∠OAB＝54°， ∴∠AOB＝180°﹣54°﹣54°＝72°， ∴∠ACB＝ ∠AOB＝36°． 故选：C． 6．一个布袋里装有 2 个红球、3 个黄球和 5 个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是黄 球的概率为（ ） A． B． C． D． 【分析】用黄色小球的个数除以总个数可得． 【解答】解：搅匀后任意摸出一个球，是黄球的概率为 ＝ ， 故选：B． 7．天虹商场一月份鞋帽专柜的营业额为 100 万元，三月份鞋帽专柜的营业额为 150 万元．设一到三月每月 平均增长率为 x，则下列方程正确的是（ ） A．100（1+2x）＝150 B．100（1+x）2＝150 C．100（1+x）+100（1+x）2＝150 D．100+100（1+x）+100（1+x）2＝150 【分析】可设每月营业额平均增长率为 x，则四月份的营业额是 100（1+x），五月份的营业额是 100（1+x） （1+x），则可以得到方程即可． 【解答】解：设四、五两个月每月的平均增长率是 x． 根据题意得：100（1+x）2＝150， 故选：B． 8．如图，在同一平面直角坐标系中，一次函数 y1＝kx+b（k、b 是常数，且 k≠0）与反比例函数 y2＝ （c 是常数，且 c≠0）的图象相交于 A（﹣3，﹣2），B（2，m）两点，则不等式 y1＞y2 的解集是（ ） A．﹣3＜x＜2 B．x＜﹣3 或 x＞2 C．﹣3＜x＜0 或 x＞2 D．0＜x＜2 【分析】一次函数 y1＝kx+b 落在与反比例函数 y2＝ 图象上方的部分对应的自变量的取值范围即为所求． 【解答】解：∵一次函数 y1＝kx+b（k、b 是常数，且 k≠0）与反比例函数 y2＝ （c 是常数，且 c≠0） 的图象相交于 A（﹣3，﹣2），B（2，m）两点， ∴不等式 y1＞y2 的解集是﹣3＜x＜0 或 x＞2． 故选：C． 9．如图是二次函数 y＝ax2+bx+c 图象的一部分，其对称轴是 x＝﹣1，且过点（﹣3，0），说法： ① abc＜0； ② 2a﹣b＝0； ③ ﹣a+c＜0； ④ 若（﹣5，y1）、（ ，y2）是抛物线上两点，则 y1＞y2，其中说法正确的有 （ ）个． A．1 B．2 C．3 D．4 【分析】根据抛物线开口方向得到 a＞0，根据抛物线的对称轴得 b＝2a＞0，则 2a﹣b＝0，则可对 ② 进 行判断；根据抛物线与 y 轴的交点在 x 轴下方得到 c＜0，则 abc＜0，于是可对 ① 进行判断；由于 x＝﹣ 1 时，y＜0，则得到 a﹣2a+c＜0，则可对 ③ 进行判断；通过点（﹣5，y1）和点（ ，y2）离对称轴的远 近对 ④ 进行判断． 【解答】解：∵抛物线开口向上， ∴a＞0， ∵抛物线对称轴为直线 x＝﹣ ＝﹣1， ∴b＝2a＞0，则 2a﹣b＝0，所以 ② 正确； ∵抛物线与 y 轴的交点在 x 轴下方， ∴c＜0， ∴abc＜0，所以 ① 正确； ∵x＝﹣1 时，y＝a﹣b+c＜0， ∵b＝2a， ∴a﹣2a+c＜0，即﹣a+c＜0，所以 ③ 正确； ∵点（﹣5，y1）离对称轴要比点（ ，y2）离对称轴要远， ∴y1＞y2，所以 ④ 正确． 故选：D． 10．在平面直角坐标系中，若干个半径为 1 的单位长度，圆心角为 60°的扇形组成一条连续的曲线，点 P 从原点 O 出发，向右沿这条曲线做上下起伏运动（如图），点 P 在直线上运动的速度为每 1 个单位长度．点 P 在弧线上运动的速度为每秒 个单位长度，则 2019 秒时，点 P 的坐标是（ ） A．（ ， ） B．（ ，﹣ ） C．（2019， ） D．（2019，﹣ ） 【分析】设第 n 秒运动到 Pn（n 为自然数）点，根据点 P 的运动规律找出部分 Pn 点的坐标，根据坐标的 变化找出变化规律“P4n+1（ ， ），P4n+2（n+1，0），P4n+3（ ，﹣ ），P4n+4（2n+2，0）”， 依此规律即可得出结论． 【解答】解：设第 n 秒运动到 Pn（n 为自然数）点， 观察，发现规律：P1（ ， ），P2（1，0），P3（ ，﹣ ），P4（2，0），P5（ ， ），…， ∴P4n+1（ ， ），P4n+2（n+1，0），P4n+3（ ，﹣ ），P4n+4（2n+2，0）． ∵2019＝4×504+3， ∴P2019 为（ ，﹣ ）， 故选：B． 二．填空题（共 5 小题） 11．方程 x2＝﹣4x 的解是 x1＝0，x2＝﹣4 ． 【分析】根据提公因式法解方程即可求解． 【解答】解：x2＝﹣4x， x2+4x＝0， x（x+4）＝0， x1＝0，x2＝﹣4 故答案为 x1＝0，x2＝﹣4． 12．如图，将△ABC 绕点 A 逆时针旋转 140°，得到△ADE，这时点 B，C，D 恰好在同一直线上，则∠B 的度数为 20° ． 【分析】由旋转的性质可得 AB＝AD，∠BAD＝140°，由等腰三角形的性质可求∠B 的度数． 【解答】解：∵将△ABC 绕点 A 逆时针旋转 140°，得到△ADE， ∴AB＝AD，∠BAD＝140° ∴∠B＝20° 故答案为：20° 13．如图，点 B 是双曲线 y＝ （k≠0）上的一点，点 A 在 x 轴上，且 AB＝2，OB⊥AB，若∠BAO＝60°， 则 k＝ 3 ． 【分析】利用 60°余弦值可求得 OB 的长，作 AD⊥OB 于点 D，利用 60°的正弦值可求得 AD 长，利用 60°余弦值可求得 BD 长，OB﹣BD 即为点 A 的横坐标，那么 k 等于点 A 的横纵坐标的积． 【解答】解：∵AB＝2，0A⊥OB，∠ABO＝60°， ∴OA＝AB÷cos60°＝4， 作 AD⊥OB 于点 D， ∴AD＝AB×sin60°＝ ， BD＝AB×cos60°＝1， ∴OD＝OA﹣BD＝3， ∴点 B 的坐标为（3， ）， ∵B 是双曲线 y＝ 上一点， ∴k＝xy＝3 ． 故答案为：3 ． 14．如图，在边长为 2 的正方形 ABCD 中，以点 D 为圆心，AD 长为半径画 ，再以 BC 为直径画半圆， 若阴影部分 ① 的面积为 S1，阴影部分 ② 的面积为 S2，则图中 S1﹣S2 的值为 π ．（结果保留 π ） 【分析】如图，设图中 ③ 的面积为 S3．构建方程组即可解决问题． 【解答】解：如图，设图中 ③ 的面积为 S3． 由题意： ， 可得 S1﹣S2＝ π ， 故答案为 π ． 15．如图，在▱ ABCD 中，AB＝6，BC＝6 ，∠D＝30°，点 E 是 AB 边的中点，点 F 是 BC 边上一动点， 将△BEF 移沿直线 EF 折叠，得到△GEF，当 FG∥AC 时，BF 的长为 3 +3 或 3 ﹣3 ． 【分析】由平行四边形的性质得出∠B＝∠D＝30°，CD＝AB＝6，AD＝BC＝6 ，作 CH⊥AD 于 H， 则 CH＝ CD＝3，DH＝ CH＝3 ＝ AD，得出 AH＝DH，由线段垂直平分线的性质得出 CA＝CD ＝AB＝6，由等腰三角形的性质得出∠ACB＝∠B＝30°，由平行线的性质得出∠BFG＝∠ACB＝30°， 分两种情况： ① 作 EM⊥BF 于 M，在 BF 上截取 EN＝BE＝3，则∠ENB＝∠B＝30°，由直角三角形的性质得出 EM ＝ BE＝ ，BM＝NM＝ EM＝ ，得出 BN＝2BM＝3 ，再证出 FN＝EN＝3，即可得出结果； ② 作 EM⊥BC 于 M，在 BC 上截取 EN＝BE＝3，连接 EN，则∠ENB＝∠B＝30°，得出 EN∥AC，EM ＝ BE＝ ，BM＝NM＝ EM＝ ，BN＝2BM＝3 ，证出 FG∥EN，则∠G＝∠GEN，证出∠GEN ＝∠ENB＝∠B＝∠G＝30°，推出∠BEN＝120°，得出∠BEG＝120°﹣∠GEN＝90°，由折叠的性质 得∠BEF＝∠GEF＝ ∠BEG＝45°，证出∠NEF＝∠NFE，则 FN＝EN＝3，即可得出结果． 【解答】解：∵四边形 ABCD 是平行四边形， ∴∠B＝∠D＝30°，CD＝AB＝6，AD＝BC＝6 ， 作 CH⊥AD 于 H， 则 CH＝ CD＝3，DH＝ CH＝3 ＝ AD， ∴AH＝DH， ∴CA＝CD＝AB＝6， ∴∠ACB＝∠B＝30°， ∵FG∥AC， ∴∠BFG＝∠ACB＝30°， ∵点 E 是 AB 边的中点， ∴BE＝3， 分两种情况： ① 作 EM⊥BF 于 M，在 BF 上截取 EN＝BE＝3，连接 EN，如图 1 所示： 则∠ENB＝∠B＝30°， ∴EM＝ BE＝ ，BM＝NM＝ EM＝ ， ∴BN＝2BM＝3 ， 由折叠的性质得：∠BFE＝∠GFE＝15°， ∵∠NEF＝∠ENB﹣∠BFE＝15°＝∠BFE， ∴FN＝EN＝3， ∴BF＝BN+FN＝3 +3； ② 作 EM⊥BC 于 M，在 BC 上截取 EN＝BE＝3，连接 EN，如图 2 所示： 则∠ENB＝∠B＝30°， ∴EN∥AC，EM＝ BE＝ ，BM＝NM＝ EM＝ ， ∴BN＝2BM＝3 ， ∵FG∥AC，∴FG∥EN，∴∠G＝∠GEN，由折叠的性质得：∠B＝∠G＝30°，∴∠GEN＝∠ENB＝∠ B＝∠G＝30°，∵∠BEN＝180°﹣∠B﹣∠ENB＝180°﹣30°﹣30°＝120°，∴∠BEG＝120°﹣∠ GEN＝120°﹣30°＝90°，由折叠的性质得：∠BEF＝∠GEF＝ ∠BEG＝45°，∴∠NEF＝∠NEG+ ∠GEF＝30°+45°＝75°，∠NFE＝∠BEF+∠B＝45°+30°＝75°，∴∠NEF＝∠NFE，∴FN＝EN＝ 3，∴BF＝BN﹣FN＝3 ﹣3； 故答案为：3 +3 或 3 ﹣3． 三．解答题（共 8 小题） 16．解下列方程： （1）x2﹣2x﹣2＝0； （2）（x﹣1）（x﹣3）＝8． 【分析】（1）利用配方法解方程； （2）利用因式分解法解出方程． 【解答】解：（1）x2﹣2x﹣2＝0 x2﹣2x+1＝3 （x﹣1）2＝3， x﹣1＝± ， x1＝ +1，x2＝﹣ +1； （2）原方程变形为：x2﹣4x﹣5＝0 （x﹣5）（x+1）＝0 x1＝5，x2＝﹣1． 17．如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别是 A（﹣4，1），B（﹣1，2），C（﹣2， 4） （1）将△ABC 向右平移 4 个单位后得到△A1B1C1，请画出△A1B1C1，并写出点 B1 的坐标； （2）△A2B2C2 和△A1B1C1 关于原点 O 中心对称，请画出△A2B2C2，并写出点 C2 的坐标； （3）连接点 A 和点 B2，点 B 和点 A2，得到四边形 AB2A2B，试判断四边形 AB2A2B 的形状（无须说明理 由）． 【分析】（1）利用网格特点和点平移的坐标规律写出 A1、B1、C1 的坐标，然后描点即可得到△A1B1C1； （2）利用网格特点和关于原点对称的点的坐标特征写出 A2、B2、C2 的坐标，然后描点即可得到△A2B2C2； （3）证明四条相等且对角线相等可判断四边形 AB2A2B 为正方形． 【解答】解：（1）如图，△A1B1C1 为所作；点 B1 的坐标为（3，2）； （2）如图，△A2B2C2 为所作；点 C2 的坐标为（﹣2，﹣4）； （3）如图，四边形 AB2A2B 为正方形． 18．图 ① 是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字 2，3，4，5．图 ② 是一个正六边 形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子在桌面掷出后，看骰子落在桌面上（即 底面）的数字是几，就从图中的 A 点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处 开始，按第一次的方法继续…… （1）随机掷一次骰子，则棋子跳动到点 C 处的概率是 ． （2）随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点 C 处的概率． 【分析】（1）当底面数字为 2 时，可以到达点 C，根据概率公式计算即可； （2）利用列表法统计即可； 【解答】解：（1）随机掷一次骰子，则棋子跳动到点 C 处的概率是 ， 故答案为 ； （2）列表如图： 共有 16 种可能，和为 8 可以到达点 C，有 3 种情形，所以棋子最终跳动到点 C 处的概率为 ． 19．如图，AB 是 ⊙ O 的直径，BM 切 ⊙ O 于点 B，点 P 是 ⊙ O 上的一个动点（点 P 不与 A，B 两点重合）， 连接 AP，过点 O 作 OQ∥AP 交 BM 于点 Q，过点 P 作 PE⊥AB 于点 C，交 QO 的延长线于点 E，连接 PQ，OP． （1）求证：△BOQ≌△POQ； （2）若直径 AB 的长为 12． ① 当 PE＝ 6 时，四边形 BOPQ 为正方形； ② 当 PE＝ 6 时，四边形 AEOP 为菱形． 【分析】（1）根据切线的性质得∠OBQ＝90°，再根据平行线的性质得∠APO＝∠POQ，∠OAP＝∠BOQ， 加上∠OPA＝∠OAP，则∠POQ＝∠BOQ，于是根据“SAS”可判断△BOQ≌△POQ； （2） ① 利用△BOQ≌△POQ 得到∠OPQ＝∠OBQ＝90°，由于 OB＝OP，所以当∠BOP＝90°，四边 形 OPQB 为正方形，此时点 C、点 E 与点 O 重合，于是 PE＝PO＝6； ② 根据菱形的判定，当 OC＝AC， PC＝EC，四边形 AEOP 为菱形，则 OC＝ OA＝3，然后利用勾股定理计算出 PC，从而得到 PE 的长． 【解答】（1）证明：∵BM 切 ⊙ O 于点 B， ∴OB⊥BQ， ∴∠OBQ＝90°， ∵PA∥OQ， ∴∠APO＝∠POQ，∠OAP＝∠BOQ， 而 OA＝OP， ∴∠OPA＝∠OAP， ∴∠POQ＝∠BOQ， 在△BOQ 和△POQ 中 ， ∴△BOQ≌△POQ； （2）解： ① ∵△BOQ≌△POQ， ∴∠OPQ＝∠OBQ＝90°， 当∠BOP＝90°，四边形 OPQB 为矩形， 而 OB＝OP，则四边形 OPQB 为正方形，此时点 C、点 E 与点 O 重合，PE＝PO＝ AB＝6； ② ∵PE⊥AB， ∴当 OC＝AC，PC＝EC，四边形 AEOP 为菱形， ∵OC＝ OA＝3， ∴PC＝ ＝3 ， ∴PE＝2PC＝6 ． 故答案为 6，6 ． 20．参照学习函数的过程与方法，探究函数 y＝ （x≠0）的图象与性质，因为 y＝ ，即 y＝ ﹣ +1，所以我们对比函数 y＝﹣ 来探究． 列表： x … ﹣4 ﹣3 ﹣2 ﹣1 ﹣ 1 2 3 4 … y＝﹣ … 1 2 4 ﹣4 ﹣2 ﹣1 ﹣ ﹣ … y＝ … 2 3 5 ﹣3 ﹣1 0 … 描点：在平面直角坐标系中以自变量 x 的取值为横坐标，以 y＝ 相应的函数值为纵坐标，描出相应 的点如图所示； （1）请把 y 轴左边点和右边各点分别用一条光滑曲线，顺次连接起来； （2）观察图象并分析表格，回答下列问题： ① 当 x＜0 时，y 随 x 的增大而 增大 ；（“增大”或“减小”） ② y＝ 的图象是由 y＝﹣ 的图象向 上 平移 1 个单位而得到的： ③ 图象关于点 （0，1） 中心对称．（填点的坐标） （3）函数 y＝ 与直线 y＝﹣2x+1 交于点 A，B，求△AOB 的面积． 【分析】（1）用光滑曲线顺次连接即可； （2）利用图象法即可解决问题； （3）联立方程求出点 A、B 的坐标，由此即可解决问题； 【解答】解：（1）函数图象如图所示： （2） ① 当 x＜0 时，y 随 x 的增大而增大； ② y＝ 的图象是由 y＝﹣ 的图象向上平移 1 个单位而得到； ③ 图象关于点（0，1）中心对称． 故答案为：增大，上，1，（0，1）； （3）根据题意得： ＝﹣2x+1，解得：x＝±1， 当 x＝1 时，y＝﹣2x+1＝﹣1， 当 x＝﹣1 时，y＝﹣2x+1＝3， ∴交点为（1，﹣1），（﹣1，3）， 当 y＝0 时，﹣2x+1＝0，x＝ ， ∴△AOB 的面积＝ ×（3+1）× ＝1． 21．某水果商场经销一种高档水果，原价每千克 50 元，连续两次降价后每千克 32 元，若每每次下降的百 分率相同 （1）求每次下降的百分率； （2）若每千克盈利 10 元，每天可售出 500 千克，经市场调查发现，在进货价不变的情况下，商场决定 采取适当的涨价措施，若每千克涨价 1 元，日销售量将减少 20 千克，现该商场要保证每天盈利 6000 元， 且要尽快减少库存，那么每千克应涨价多少元？ 【分析】（1）设每次降价的百分率为 a，（1﹣a）2 为两次降价的百分率，50 降至 32 就是方程的平衡条件， 列出方程求解即可； （2）根据题意列出一元二次方程，然后求出其解，最后根据题意确定其值． 【解答】解：（1）设每次下降的百分率为 a，根据题意，得： 50（1﹣a）2＝32， 解得：a＝1.8（舍）或 a＝0.2， 答：每次下降的百分率为 20%； （2）设每千克应涨价 x 元，由题意，得 （10+x）（500﹣20x）＝6000， 整理，得 x2﹣15x+50＝0， 解得：x1＝5，x2＝10， 因为要尽快减少库存，所以 x＝5 符合题意． 答：该商场要保证每天盈利 6000 元，那么每千克应涨价 5 元． 22．在 Rt△ABC 中，∠BCA＝90°，∠A＜∠ABC，D 是 AC 边上一点，且 DA＝DB，O 是 AB 的中点，CE 是△BCD 的中线． （1）如图 a，连接 OC，请直接写出∠OCE 和∠OAC 的数量关系： ∠OCE＝∠OAC ； （2）点 M 是射线 EC 上的一个动点，将射线 OM 绕点 O 逆时针旋转得射线 ON，使∠MON＝∠ADB， ON 与射线 CA 交于点 N． ① 如图 b，猜想并证明线段 OM 和线段 ON 之间的数量关系； ② 若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段 ME 的长度（用含 m 的代数式表示）． 【分析】（1）结论：∠ECO＝∠OAC．理由直角三角形斜边中线定理，三角形的中位线定理解决问题即 可． （2） ① 只要证明△COM≌△AON（ASA），即可解决问题． ② 分两种情形：如图 3﹣1 中，当点 N 在 CA 的延长线上时，如图 3﹣2 中，当点 N 在线段 AC 上时，作 OH⊥AC 于 H．分别求解即可解决问题． 【解答】解：（1）结论：∠ECO＝∠OAC． 理由：如图 1 中，连接 OE． ∵∠BCD＝90°，BE＝ED，BO＝OA， ∵CE＝ED＝EB＝ BD，CO＝OA＝OB， ∴∠OCA＝∠A， ∵BE＝ED，BO＝OA， ∴OE∥AD，OE＝ AD， ∴CE＝EO． ∴∠EOC＝∠OCA＝∠ECO， ∴∠ECO＝∠OAC． 故答案为：∠OCE＝∠OAC． （2）如图 2 中， ∵OC＝OA，DA＝DB， ∴∠A＝∠OCA＝∠ABD， ∴∠COA＝∠ADB， ∵∠MON＝∠ADB， ∴∠AOC＝∠MON， ∴∠COM＝∠AON， ∵∠ECO＝∠OAC， ∴∠MCO＝∠NAO， ∵OC＝OA， ∴△COM≌△AON（ASA）， ∴OM＝ON． ② 如图 3﹣1 中，当点 N 在 CA 的延长线上时， ∵∠CAB＝30°＝∠OAN+∠ANO，∠AON＝15°， ∴∠AON＝∠ANO＝15°， ∴OA＝AN＝m， ∵△OCM≌△OAN， ∴CM＝AN＝m， 在 Rt△BCD 中，∵BC＝m，∠CDB＝60°， ∴BD＝ m， ∵BE＝ED， ∴CE＝ BD＝ m， ∴EM＝CM+CE＝m+ m． 如图 3﹣2 中，当点 N 在线段 AC 上时，作 OH⊥AC 于 H． ∵∠AON＝15°，∠CAB＝30°， ∴∠ONH＝15°+30°＝45°， ∴OH＝HN＝ m， ∵AH＝ m， ∴CM＝AN＝ m﹣ m， ∵EC＝ m， ∴EM＝EC﹣CM＝ m﹣（ m﹣ m）＝ m﹣ m， 综上所述，满足条件的 EM 的值为 m+ m 或 m﹣ m． 23．如图，若 b 是正数．直线 l：y＝b 与 y 轴交于点 A，直线 a：y＝x﹣b 与 y 轴交于点 B；抛物线 L：y＝ ﹣x2+bx 的顶点为 C，且 L 与 x 轴右交点为 D． （1）若 AB＝6，求 b 的值，并求此时 L 的对称轴与 a 的交点坐标； （2）当点 C 在 l 下方时，求点 C 与 l 距离的最大值； （3）设 x0≠0，点（x0，y1），（x0，y2），（x0，y3）分别在 l，a 和 L 上，且 y3 是 y1，y2 的平均数，求点（x0， 0）与点 D 间的距离； （4）在 L 和 a 所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出 b ＝2019 和 b＝2019.5 时“美点”的个数． 【分析】（1）当 x＝0 时，y＝x﹣b＝﹣b，所以 B （0，﹣b），而 AB＝6，而 A（0，b），则 b﹣（﹣b） ＝6，b＝3．所以 L：y＝﹣x2+3x，对称轴 x＝1.5，当 x＝1.5 吋，y＝x﹣3＝﹣1.5，于是得到结论． （2）由 y＝﹣（x﹣ ）2+ ，得到 L 的顶点 C（ ， ），由于点 C 在 l 下方，于是得到结论； （3）由題意得到 y3＝ ，即 y1+y2＝2y3，得 b+x0﹣b＝2（﹣x02+bx0）解得 x0＝0 或 x0＝b﹣ ．但 x0≠0，取 x0＝b﹣ ，得到右交点 D（b，0）．于是得到结论； （4） ① 当 b＝2019 时，抛物线解析式 L：y＝﹣x2+2019x 直线解析式 a：y＝x﹣2019，美点”总计 4040 个点， ② 当 b＝2019.5 时，抛物线解析式 L：y＝﹣x2+2019.5x，直线解析式 a：y＝x﹣2019.5，“美点” 共有 1010 个． 【解答】解：（1）当 x＝0 时，y＝x﹣b＝﹣b， ∴B （0，﹣b）， ∵AB＝6，而 A（0，b）， ∴b﹣（﹣b）＝6， ∴b＝3． ∴L：y＝﹣x2+3x， ∴L 的对称轴 x＝1.5， 当 x＝1.5 吋，y＝x﹣3＝﹣1.5， ∴L 的对称轴与 a 的交点为（1.5，﹣1.5 ）； （2）y＝﹣（x﹣ ）2+ ， ∴L 的顶点 C（ ， ）， ∵点 C 在 l 下方， ∴C 与 l 的距离 b﹣ ＝﹣ （b﹣2）2+1≤1， ∴点 C 与 1 距离的最大值为 1； （3）由题意得 y3＝ ，即 y1+y2＝2y3， 得 b+x0﹣b＝2（﹣x02+bx0） 解得 x0＝0 或 x0＝b﹣ ．但 x0≠0，取 x0＝b﹣ ， 对于 L，当 y＝0 吋，0＝﹣x2+bx，即 0＝﹣x（x﹣b）， 解得 x1＝0，x2＝b， ∵b＞0， ∴右交点 D（b，0）． ∴点（x0，0）与点 D 间的距离 b﹣（b﹣ ）＝ ； （4） ① 当 b＝2019 时，抛物线解析式 L：y＝﹣x2+2019x， 直线解析式 a：y＝x﹣2019 联立上述两个解析式可得：x1＝﹣1，x2＝2019， ∴可知每一个整数 x 的值都对应的一个整数 y 值，且﹣1 和 2019 之间（包括﹣1 和﹣2019）共有 2021 个 整数； ∵另外要知道所围成的封闭图形边界分两部分：线段和抛物线， ∴线段和抛物线上各有 2021 个整数点， ∴总计 4042 个点， ∵这两段图象交点有 2 个点重复， ∴美点”的个数：4042﹣2＝4040（个）； ② 当 b＝2019.5 时， 抛物线解析式 L：y＝﹣x2+2019.5x， 直线解析式 a：y＝x﹣2019.5， 联立上述两个解析式可得：x1＝﹣1，x2＝2019.5， ∴当 x 取整数时，在一次函数 y＝x﹣2019.5 上，y 取不到整数值，因此在该图象上“美点”为 0， 在二次函数 y＝x2+2019.5x 图象上，当 x 为偶数时，函数值 y 可取整数， 可知﹣1 到 2019.5 之 间有 1010 个偶数，因此“美点”共有 1010 个． 故 b＝2019 时“美点”的个数为 4040 个，b＝2019.5 时“美点”的个数为 1010 个．