2020-2021北京三帆中学初三10月数学月考试题（PDF版） 9页

1 初三数学 10 月月考试题 一、选择题（每题 3 分） 01.如图，将一张矩形的纸对折，旋转 90°后再对折，然后沿着右图中的虚线剪下，则剪下的纸片打开后的形 状一定为 【 】 A.三角形 B.矩形 C.菱形 D.正方形 02.如图，将 ABC 绕点 A 逆时针旋转 100°，得到 ADE .若点 D 在线段 BC 的延长线上，则 B 的大小为 【 】 A.30° B.40° C.50° D.60° 03.若要得到函数  21 2y x   的图像，只需要将函数 2y x 的图像 【 】 A.先向左平移 1 个单位长度，再向上平移 2 个单位长度 B.先向右平移 1 个单位长度，再向上平移 2 个单位长度 C.先向左平移 1 个单位长度，再向下平移 2 个单位长度 D.先向右平移 1 个单位长度，再向下平移 2 个单位长度 04.若关于 x 的方程  11 2 3mm x x   是关于 x 的一元二次方程，则 m 的取值为 【 】 A. 1m  B. 1m   C. 1m   D. 1m   05. O 是四边形 ABCD 的外接圆，AC 平分 BAD ,则正确结论是 【 】 A.AB=AD; B.BC=CD; C.  AB BD ; D. 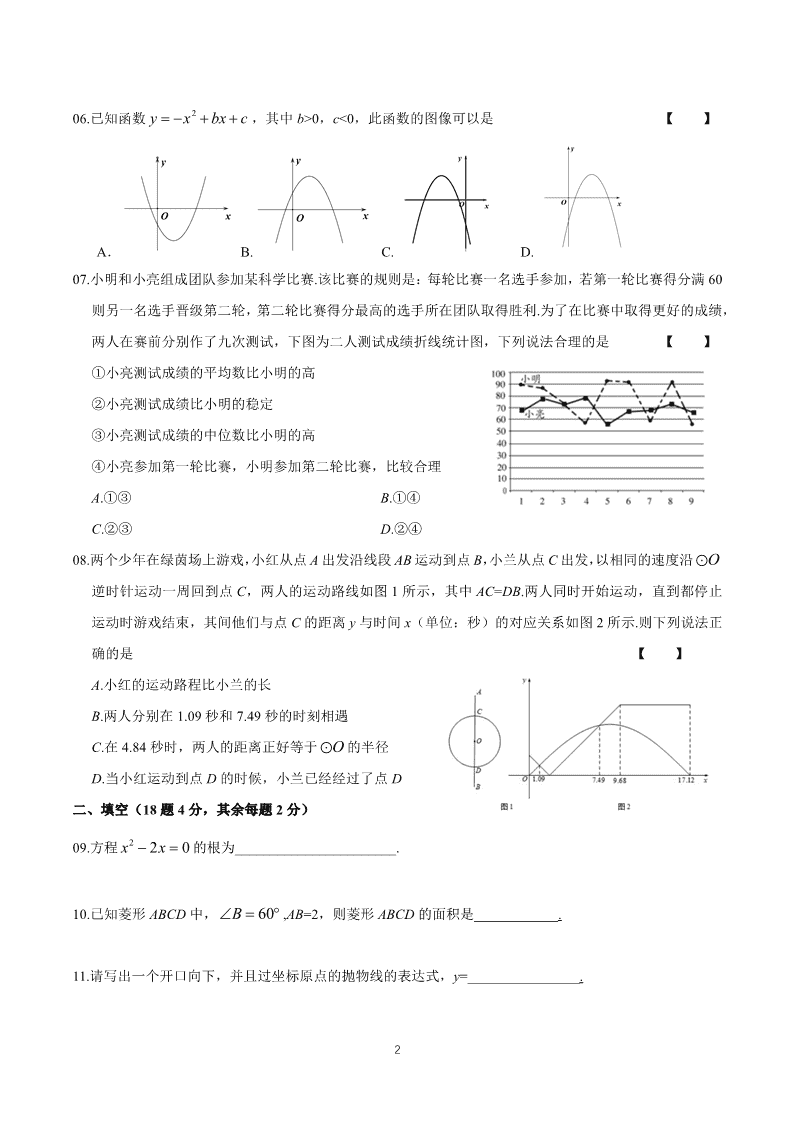 AB BD 2 06.已知函数 2y x bx c    ，其中 b>0，c<0，此函数的图像可以是 【 】 A． B. C. D. 07.小明和小亮组成团队参加某科学比赛.该比赛的规则是：每轮比赛一名选手参加，若第一轮比赛得分满 60 则另一名选手晋级第二轮，第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩， 两人在赛前分别作了九次测试，下图为二人测试成绩折线统计图，下列说法合理的是 【 】 ①小亮测试成绩的平均数比小明的高 ②小亮测试成绩比小明的稳定 ③小亮测试成绩的中位数比小明的高 ④小亮参加第一轮比赛，小明参加第二轮比赛，比较合理 A.①③ B.①④ C.②③ D.②④ 08.两个少年在绿茵场上游戏，小红从点 A 出发沿线段 AB 运动到点 B，小兰从点 C 出发，以相同的速度沿 O 逆时针运动一周回到点 C，两人的运动路线如图 1 所示，其中 AC=DB.两人同时开始运动，直到都停止 运动时游戏结束，其间他们与点 C 的距离 y 与时间 x（单位：秒）的对应关系如图 2 所示.则下列说法正 确的是 【 】 A.小红的运动路程比小兰的长 B.两人分别在 1.09 秒和 7.49 秒的时刻相遇 C.在 4.84 秒时，两人的距离正好等于 O 的半径 D.当小红运动到点 D 的时候，小兰已经经过了点 D 二、填空（18 题 4 分，其余每题 2 分） 09.方程 2 2 0x x  的根为_______________________. 10.已知菱形 ABCD 中， 60B   ,AB=2，则菱形 ABCD 的面积是____________. 11.请写出一个开口向下，并且过坐标原点的抛物线的表达式，y=________________. 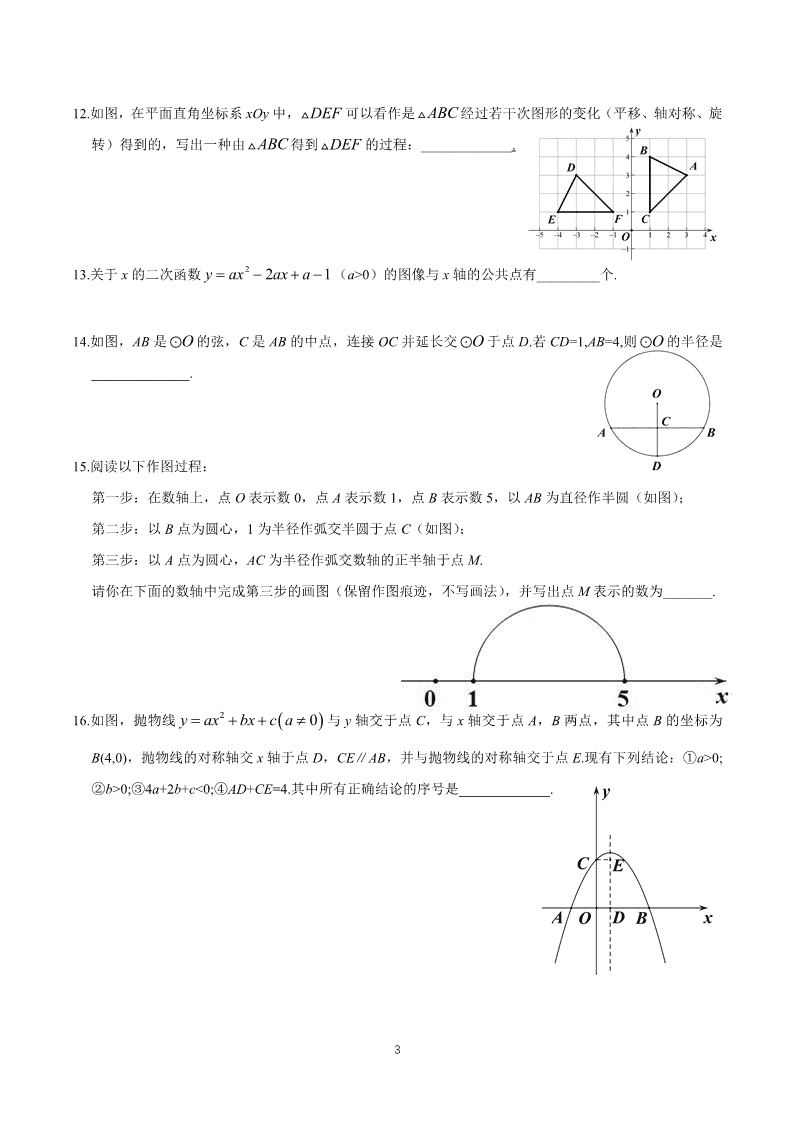3 12.如图，在平面直角坐标系 xOy 中， DEF 可以看作是 ABC 经过若干次图形的变化（平移、轴对称、旋 转）得到的，写出一种由 ABC 得到 DEF 的过程：_____________. 13.关于 x 的二次函数 2 2 1y ax ax a    （a>0）的图像与 x 轴的公共点有_________个. 14.如图，AB 是 O 的弦，C 是 AB 的中点，连接 OC 并延长交 O 于点 D.若 CD=1,AB=4,则 O 的半径是 ______________. 15.阅读以下作图过程： 第一步：在数轴上，点 O 表示数 0，点 A 表示数 1，点 B 表示数 5，以 AB 为直径作半圆（如图）； 第二步：以 B 点为圆心，1 为半径作弧交半圆于点 C（如图）； 第三步：以 A 点为圆心，AC 为半径作弧交数轴的正半轴于点 M. 请你在下面的数轴中完成第三步的画图（保留作图痕迹，不写画法），并写出点 M 表示的数为_______. 16.如图，抛物线  2 0y ax bx c a    与 y 轴交于点 C，与 x 轴交于点 A，B 两点，其中点 B 的坐标为 B(4,0)，抛物线的对称轴交 x 轴于点 D，CE∥AB，并与抛物线的对称轴交于点 E.现有下列结论：①a>0; ②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正确结论的序号是_____________. 4 三、解答 17.解下列一元二次方程： （1）  23 1 15x  （2） 23 4 2 0x x   18.已知一元二次方程 0)12( 22  mmxmx （1）求证：此方程有两个不相等的实数根； （2）若抛物线 2 2(2 1) 0y x m x m m      经过原点，求 m 的值. 19.已知二次函数 2 2 3y x x   . （1）将 2 2 3y x x   化成 2( )y a x h k   的形式为 ； （2）此函数与 x 轴的交点坐标为 ； （3）在平面直角坐标系 xOy 中，画出这个二次函数的图像（不用列表．．．．）； （4）直接写出当 2 3x   时，y 的取值范围. 5 20.如图，菱形 ABCD 中，AC 与 BD 交于点 O，DE∥AC, 1 2DE AC . （1）求证：四边形 OCED 是矩形； （2）连结 AE，交 OD 于点 F，连结 CF.若 CF=CE=1,求 AC 长. 21.如图，四边形 ABCD 内接于 O ， 4, 4 2OC AC  . （1）求点 O 到 AC 的距离; （2）求∠ADC 的度数. 22.小明根据学习函数的经验，对函数 4 25 4y x x   的图像与性质进行了探究. 下面是小明的探究过程，请补充完整： （1）自变量 x 的取值范围是全体实数，x 与 y 的几组对应数值如下表： 其中 m= ； （2）如图，在平面直角坐标系 xOy 中，描出了以上表中各组对应值为坐标的点，根据描出的点，画出该 函数的图像； （3）观察函数图像，写出一条该函数的性质 ； （4）进一步探究函数图像发现： ①方程 4 25 4 0x x   有 个互不相等的实数根； ②有两个点 1 1( )x y， 和 2 2( )x y， 在此函数图像上，当 2 1 2x x  时，比较 1y 和 2y 的大小关系为： 1y 2y （填“>”、“<”或“=”）； x … 9 4  11 5  2 3 2  5 4  1 1 2  1 4  0 1 4 1 2 1 5 4 3 2 2 11 5 9 4 … y … 4.3 3.2 0 -2.2 -1.4 0 2.8 3.7 4 3.7 2.8 0 -1.4 -2.2 m 3.2 4.3 … 6 ③ 若关于 x 的方程 4 25 4x x a   有 4 个互不相等的实数根，则 a 的取值范围是 . 7 23.已知二次函数 2 4 3y ax ax a   . （1）该二次函数图像的对称轴是直线 x  ； （2）若该二次函数的图像开口向下，当1 4x  时，y 的最大值是 2，求抛物线的解析式； （3）若对于该抛物线上的两点 1 1( )P x y， , 2 2( )Q x y， ,当 1 1t x t   ， 2 5x  时，均满足 1 2y y ，请结 合图像，直接写出 t 的取值范围. 24.在等腰△ABC 中，AB=AC，将线段 BA 绕 B 顺时针旋转到 BD，使 BD  AC 于 H，连结 AD 并延交 BC 的 延长线于点 P. （1）依题意补全图形； （2）若 2BAC ，求∠BDA 的大小（用含 的式子表示）； （3）小明作了点 D 关于直线 BC 的对称点 E，从而用等式表示线段 DP 与 BC 之间的数量关系，请你用 小明的思路去补全图形并证明线段 DP 与 BC 之间的数量关系. 8 25. 对于平面直角坐标系 xOy 中的点 P，给出如下定义:记点 P 到 x 轴的距离为 1d ，到 y 轴的距离为 2d ，若 1 2d d ，则称 1d 为点 P 的最大距离；若 1 2d d ，则称 2d 为点 P 的最大距离. 例如：点 P ( 3 ) ，4 到 x 轴的距离为 4，到 y 轴的距离为 3，因为3 4 ，所以点 P 的最大距离为 4. （1）①点 )5,2( A 的最大距离为 ； ②若点 )2,(aB 的最大距离为 5，则 a 的值为 ； （2）若点 C 在直线 2y x   上，且点 C 的最大距离为 5，求点 C 的坐标； （3）若 O 上存在．．点 M，使点 M 的最大距离为 5，直接写出 O 的半径 r 的取值范围.