人教版九年级数学下册-期末检测题 6页

期末检测题 (时间：100 分钟满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．(玉林中考)sin30°＝( B ) A． 2 2 B．1 2C． 3 2 D． 3 3 2．(2020·凉山州)如图，下列几何体的左视图不是矩形的是( B ) 3．(2020·黔西南州)如图，某停车场入口的栏杆 AB，从水平位置绕点 O 旋转到 A′B′的位 置，已知 AO 的长为 4 米．若栏杆的旋转角∠AOA′＝α，则栏杆 A 端升高的高度为( B ) A． 4 sinα 米 B．4sinα米 C． 4 cosα 米 D．4cosα米 第 3 题图 第 4 题图 第 5 题图 第 6 题图 4．(新疆中考)如图，在△ABC 中，D，E 分别是 AB，AC 的中点，下列说法中不正确的 是( D ) A．DE＝1 2BCB．AD AB ＝AE AC C．△ADE∽△ABCD．S△ADE∶S△ABC＝1∶2 5．(2020·怀化)在同一平面直角坐标系中，一次函数 y1＝k1x＋b 与反比例函数 y2＝k2 x (x＞ 0)的图象如图所示．则当 y1＞y2 时，自变量 x 的取值范围为( D ) A．x＜1B．x＞3C．0＜x＜1D．1＜x＜3 6．(2020·宜宾)如图，AB 是⊙O 的直径，点 C 是圆上一点，连接 AC 和 BC，过点 C 作 CD⊥AB 于点 D，且 CD＝4，BD＝3，则⊙O 的周长是( A ) A．25 3 πB．50 3 πC．625 9 πD．625 36 π 7．(2020·自贡)函数 y＝k x 与 y＝ax2＋bx＋c 的图象如图所示，则函数 y＝kx－b 的大致图 象为( D ) 8．如图，要在宽为 22 米的九州大道两边安装路灯，路灯的灯臂 CD 长 2 米，且与灯柱 BC 成 120°角，路灯采用圆锥形灯罩，灯罩的轴线 DO 与灯臂 CD 垂直，当灯罩的轴线 DO 通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱 BC 高度应该设计为( D ) A.(11－2 2)米 B．(11 3－2 2)米 C．(11－2 3)米 D．(11 3－4)米 第 8 题图 第 9 题图 第 10 题图 9．(2020·苏州)如图，平行四边形 OABC 的顶点 A 在 x 轴的正半轴上，点 D(3，2)在对角 线 OB 上，反比例函数 y＝k x(k＞0，x＞0)的图象经过 C，D 两点．已知平行四边形 OABC 的 面积是15 2 ，则点 B 的坐标为( B ) A．(4，8 3) B．(9 2 ，3) C．(5，10 3 ) D．(24 5 ，16 5 ) 10．(2020·遂宁)如图，在正方形 ABCD 中，点 E 是边 BC 的中点，连接 AE，DE，分别 交 BD，AC 于点 P，Q，过点 P 作 PF⊥AE 交 CB 的延长线于 F，下列结论： ①∠AED＋∠EAC＋∠EDB＝90°；②AP＝FP；③AE＝ 10 2 AO；④若四边形 OPEQ 的 面积为 4，则该正方形 ABCD 的面积为 36；⑤CE·EF＝EQ·DE. 其中正确的结论有( B ) A．5 个 B．4 个 C．3 个 D．2 个 二、填空题(每小题 3 分，共 15 分) 11．(上海中考)已知反比例函数 y＝k x(k≠0)，如果在这个函数图象所在的每一个象限内， y 的值随着 x 的值增大而减小，那么 k 的取值范围是 k>0． 12．如图，在▱ABCD 中，点 E 是边 BC 上一点，AE 交 BD 于点 F，若 BE＝2，EC＝3， 则BF DF 的值为2 5 ． 第 12 题图 第 13 题图 第 14 题图 第 15 题图 13．(2020·达州)如图，小明为测量校园里一棵大树 AB 的高度，在树底部 B 所在的水平 面内，将测角仪 CD 竖直放在与 B 相距 8m 的位置，在 D 处测得树顶 A 的仰角为 52°.若测 角仪的高度是 1m，则大树 AB 的高度约为__11_m__．(结果精确到 1m．参考数据：sin52° ≈0.78，cos52°≈0.61，tan52°≈1.28) 14．(2020·鄂州)如图，点 A 是双曲线 y＝1 x(x＜0)上一动点，连接 OA，作 OB⊥OA，且使 OB＝3OA，当点 A 在双曲线 y＝1 x 上运动时，点 B 在双曲线 y＝k x 上移动，则 k 的值为__－9__． 15．(2020·岳阳)如图，AB 为半圆 O 的直径，M，C 是半圆上的三等分点，AB＝8，BD 与半圆 O 相切于点 B.点 P 为 AM 上一动点(不与点 A，M 重合)，直线 PC 交 BD 于点 D，BE ⊥OC 于点 E，延长 BE 交 PC 于点 F，则下列结论正确的是__②⑤__．(写出所有正确结论的 序号) ①PB＝PD；② BC 的长为4 3 π；③∠DBE＝45°；④△BCF∽△PFB；⑤CF·CP 为定值． 三、解答题(共 75 分) 16．(8 分)如图，在 Rt△ABC 中，∠BAC＝90°，点 D 在 BC 边上，且△ABD 是等边三 角形．若 AB＝2，求△ABC 的周长．(结果保留根号) 解：△ABC 的周长是 6＋2 3 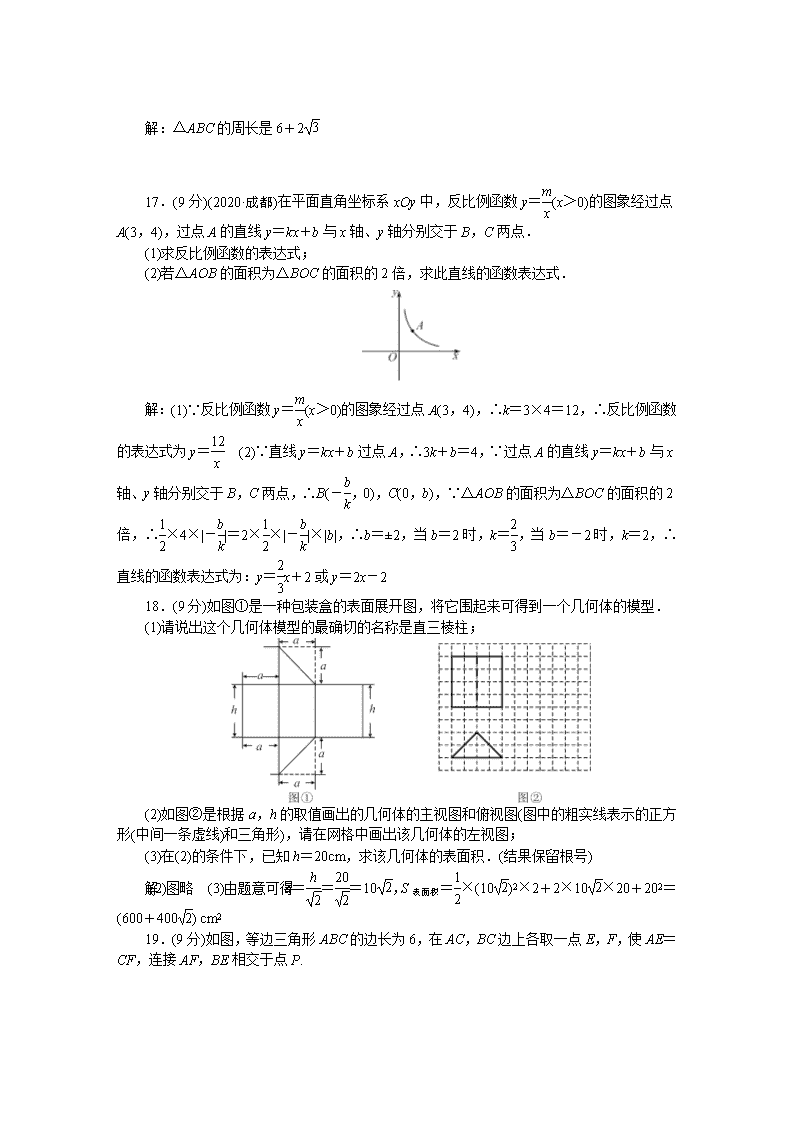17．(9 分)(2020·成都)在平面直角坐标系 xOy 中，反比例函数 y＝m x (x＞0)的图象经过点 A(3，4)，过点 A 的直线 y＝kx＋b 与 x 轴、y 轴分别交于 B，C 两点． (1)求反比例函数的表达式； (2)若△AOB 的面积为△BOC 的面积的 2 倍，求此直线的函数表达式． 解：(1)∵反比例函数 y＝m x(x＞0)的图象经过点 A(3，4)，∴k＝3×4＝12，∴反比例函数 的表达式为 y＝12 x (2)∵直线 y＝kx＋b 过点 A，∴3k＋b＝4，∵过点 A 的直线 y＝kx＋b 与 x 轴、y 轴分别交于 B，C 两点，∴B(－b k ，0)，C(0，b)，∵△AOB 的面积为△BOC 的面积的 2 倍，∴1 2 ×4×|－b k|＝2×1 2 ×|－b k|×|b|，∴b＝±2，当 b＝2 时，k＝2 3 ，当 b＝－2 时，k＝2，∴ 直线的函数表达式为：y＝2 3x＋2 或 y＝2x－2 18．(9 分)如图①是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型． (1)请说出这个几何体模型的最确切的名称是直三棱柱； (2)如图②是根据 a，h 的取值画出的几何体的主视图和俯视图(图中的粗实线表示的正方 形(中间一条虚线)和三角形)，请在网格中画出该几何体的左视图； (3)在(2)的条件下，已知 h＝20cm，求该几何体的表面积．(结果保留根号) 解：(2)图略 (3)由题意可得：a＝ h 2 ＝20 2 ＝10 2，S 表面积＝1 2 ×(10 2)2×2＋2×10 2×20 ＋202＝(600＋400 2) cm2 19．(9 分)如图，等边三角形 ABC 的边长为 6，在 AC，BC 边上各取一点 E，F，使 AE ＝CF，连接 AF，BE 相交于点 P. (1)求证：AF＝BE，并求∠APB 的度数； (2)若 AE＝2，试求 AP·AF 的值． 解：(1)∵△ABC 为等边三角形，∴AB＝AC，∠C＝∠CAB＝60°，又∵AE＝CF， ∴△ABE≌△CAF(SAS)，∴AF＝BE，∠ABE＝∠CAF.又∵∠APE＝∠BPF＝∠ABP＋∠BAP， ∴∠APE＝∠BAP＋∠CAF＝60°，∴∠APB＝180°－∠APE＝120° (2)∵∠C＝∠APE＝ 60°，∠PAE＝∠CAF，∴△APE∽△ACF，∴AP AC ＝AE AF ，即AP 6 ＝ 2 AF ，∴AP·AF＝12 20．(9 分)(2020·黄冈)已知：如图，一次函数的图象与反比例函数的图象交于 A，B 两点， 与 y 轴正半轴交于点 C，与 x 轴负半轴交于点 D，OB＝ 5，tan∠DOB＝1 2. (1)求反比例函数的解析式； (2)当 S△ACO＝1 2S△OCD 时，求点 C 的坐标． 解：分别过点 B，A 作 BM⊥x 轴，AN⊥y 轴，垂足为点 M，N，(1)在 Rt△BOM 中，OB ＝ 5，tan∠DOB＝1 2 ，∴BM＝1，OM＝2，∴点 B(－2，－1)，∴k＝(－2)×(－1)＝2，∴反 比例函数的关系式为 y＝2 x (2)∵S△ACO＝1 2S△OCD，∴OD＝2AN，又∵△ANC∽△DOC，∴AN DO ＝NC OC ＝CA CD ＝1 2 ，设 AN＝a，CN＝b，则 OD＝2a，OC＝2b，∵S△OAN＝1 2|k|＝1＝1 2ON·AN＝ 1 2 ×3b×a，∴ab＝2 3 ①，由△BMD∽△CNA 得MD AN ＝BM CN ，即2－2a a ＝1 b ，也就是 a＝ 2b 2b＋1 ②， 由①②可求得 b＝1，b＝－1 3(舍去)，∴OC＝2b＝2，∴点 C(0，2) 21．(10 分)(2020·河南)位于河南省登封市境内的元代观星台，是中国现存最早的天文台， 也是世界文化遗产之一． 某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度．如图所示，他们在 地面一条水平步道 MP 上架设测角仪，先在点 M 处测得观星台最高点 A 的仰角为 22°，然 后沿 MP 方向前进 16m 到达点 N 处，测得点 A 的仰角为 45°.测角仪的高度为 1.6m. (1)求观星台最高点 A 距离地面的高度(结果精确到 0.1m．参考数据：sin22°≈0.37，cos22 °≈0.93，tan22°≈0.40， 2≈1.41)； (2)“景点简介”显示，观星台的高度为 12.6m．请计算本次测量结果的误差，并提出一 条减小误差的合理化建议． 解：(1)过 A 作 AD⊥PM 于 D，延长 BC 交 AD 于 E，则四边形 BMNC，四边形 BMDE 是 矩形，∴BC＝MN＝16m，DE＝CN＝BM＝1.6m，∵∠AEB＝90°，∠ACE＝45°，∴△ACE 是等腰直角三角形，∴CE＝AE，设 AE＝CE＝x，∴BE＝16＋x，∵∠ABE＝22°，∴tan22 °＝AE BE ＝ x 16＋x ≈0.40，∴x≈10.7(m)，∴AD＝10.7＋1.6＝12.3(m)，答：观星台最高点 A 距 离地面的高度约为 12.3m (2)∵“景点简介”显示，观星台的高度为 12.6m，∴本次测量结果的误差为 12.6－12.3 ＝0.3(m)，减小误差的合理化建议为：可以通过多次测量取平均值的方法来减小误差 22．(10 分)(2020·常德)如图，已知 AB 是⊙O 的直径，C 是⊙O 上的一点，D 是 AB 上的 一点，DE⊥AB 于 D，DE 交 BC 于 F，且 EF＝EC. (1)求证：EC 是⊙O 的切线； (2)若 BD＝4，BC＝8，圆的半径 OB＝5，求切线 EC 的长． 解：(1)连接 OC，∵OC＝OB，∴∠OBC＝∠OCB，∵DE⊥AB，∴∠OBC＋∠DFB＝90°， ∵EF＝EC，∴∠ECF＝∠EFC＝∠DFB，∴∠OCB＋∠ECF＝90°，∴OC⊥EC，∴EC 是 ⊙O 的切线 (2)∵AB 是⊙O 的直径，∴∠ACB＝90°，∵OB＝5，∴AB＝10，∴AC＝ AB2－BC2＝ 100－64＝6，∵cos∠ABC＝BD BF ＝BC AB ，∴ 8 10 ＝ 4 BF ，∴BF＝5，∴CF＝BC－BF ＝3，∵∠ABC＋∠A＝90°，∠ABC＋∠BFD＝90°，∴∠BFD＝∠A，∴∠A＝∠BFD＝∠ECF ＝∠EFC，∵OA＝OC，∴∠OCA＝∠A＝∠BFD＝∠ECF＝∠EFC，∴△OAC∽△ECF，∴EC OA ＝CF AC ，∴EC＝OA·CF AC ＝5×3 6 ＝5 2 23．(11 分)如图，在 Rt△ABC 中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB 于点 D.点 P 从点 D 出发，沿线段 DC 向点 C 运动，点 Q 从点 C 出发，沿线段 CA 向点 A 运动，两点同 时出发，速度都为每秒 1 个单位长度，当点 P 运动到点 C 时，两点都停止．设运动时间为 t 秒． (1)求线段 CD 的长； (2)设△CPQ 的面积为 S，求 S 与 t 之间的函数关系式，并确定在运动过程中是否存在某 一时刻 t，使得 S△CPQ∶S△ABC＝9∶100？若存在，求出 t 的值；若不存在，说明理由； (3)当 t 为何值时，△CPQ 为等腰三角形？ 解：(1)线段 CD 的长为 4.8 (2)过点 P 作 PH⊥AC，垂足为 H，由题意可知 DP＝t，CQ ＝t，则 CP＝4.8－t.由△CHP∽△BCA 得PH AC ＝PC AB ，∴PH 8 ＝4.8－t 10 ，∴PH＝96 25 －4 5t，∴S△CPQ ＝1 2CQ·PH＝1 2t(96 25 －4 5t)＝－2 5t2＋48 25t.设存在某一时刻 t，使得 S△CPQ∶S△ABC＝9∶100.∵S△ABC＝ 1 2 ×6×8＝24，且 S△CPQ∶S△ABC＝9∶100，∴(－2 5t2＋48 25t)∶24＝9∶100，整理得 5t2－24t＋27 ＝0，即(5t－9)(t－3)＝0，解得 t＝9 5 或 t＝3，∵0≤t≤4.8，∴当 t＝9 5 或 t＝3 时，S△CPQ∶S△ABC ＝9∶100 (3)①若 CQ＝CP，则 t＝4.8－t.解得 t＝2.4；②若 PQ＝PC，作 PH⊥QC 于点 H， ∴QH＝CH＝1 2QC＝t 2 ，∵△CHP∽△BCA，∴CH BC ＝CP AB ，∴ t 2 6 ＝4.8－t 10 ，解得 t＝144 55 ；③若 QC ＝QP，过点 Q 作 QE⊥CP，垂足为 E，同理可得 t＝24 11.综上所述：当 t 为 2.4 或144 55 或24 11 时， △CPQ 为等腰三角形