苏教版九年级数学上册期中考试调研测试卷 8页

第一学期期中考试 九年级 数学试卷 （满分：120 分 考试时间：150 分钟） 成绩 一．选择题把下列各题的正确答案前面的英文字母填入下表（每题 3 分，共 18 分）： 题号 1 2 3 4 5 6 答案 1．下列计算 正确的是 A． 2 3 5  B． 8 4 2 C． 27 3 3  D．  23 3   2．甲、乙两名同学 100 米短跑进行 5 次测试，他们的成绩通过计算得： x 甲= x 乙， S2 甲=0.027，S2 乙=0.026，下列说法正确的是 A．甲比乙短跑成绩稳定 B. 甲短跑成绩比乙好 C.乙比甲短跑成绩稳定 D. 乙短跑成绩比甲好 3．某种商品原价 168 元，连续两次降价 a %后售价为 128 元. 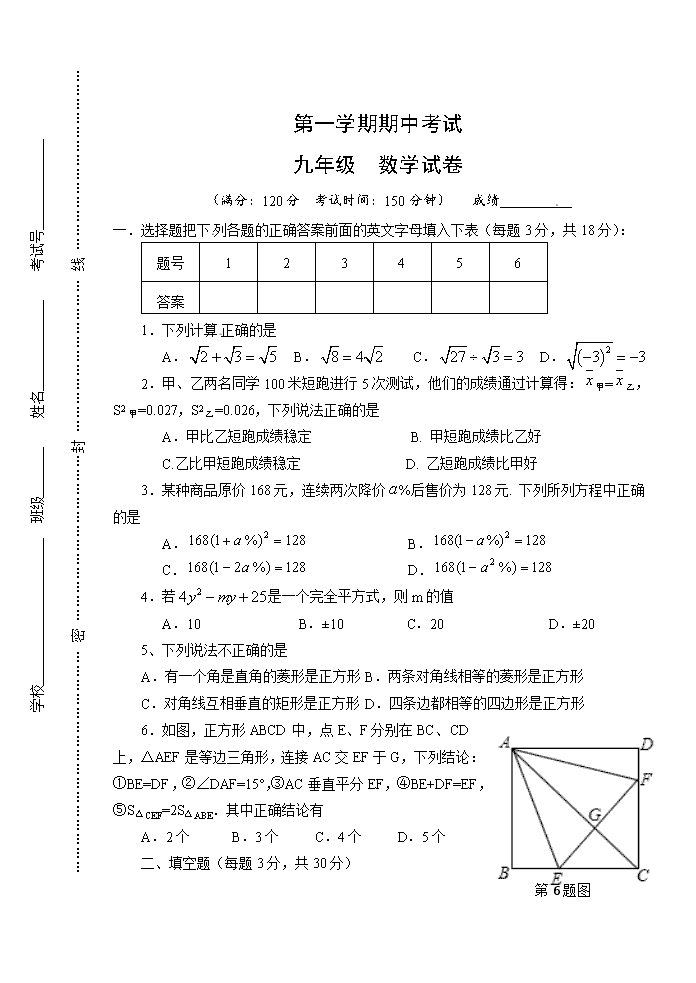下列所列方程中正确 的是 A． 128)% 1(168 2  a B． 128)% 1(168 2  a C． 128)% 21(168  a D． 128)% 1(168 2  a 4．若 24 25y my  是一个完全平方式，则 m 的值 A．10 B．±10 C．20 D．±20 5、下列说法不正确的是 A．有一个角是直角的菱形是正方形 B．两条对角线相等的菱形是正方形 C．对角线互相垂直的矩形是正方形 D．四条边都相等的四边形是正方形 6．如图，正方形 ABCD 中，点 E、F 分别在 BC、CD 上， △AEF 是等边三角形，连接 AC 交 EF 于 G，下列结论： ①BE=DF，②∠DAF=15°，③AC 垂直平分 EF，④BE+DF=EF， ⑤S△CEF=2S△ABE．其中正确结论有 A．2 个 B．3 个 C．4 个 D．5 个 二、填空题（每题 3 分，共 30 分） 第 6 题图 学 校 班 级 姓 名 考 试 号 … … … … … … … … … … … … … … … … 密 … … … … … … … … … … … … 封 … … … … … … … … … … … 线 … … … … … … … … … … … … … C A 60° B 7.式子 x21 有意义，则 x 取值为__________。 8.方程方程 2 4x x 的根为_________。 9.已知样本 0、2、x、4 的极差是 6，则样本的平均数为__________。 10.已知菱形的两条对角线分别为 6cm 和 8cm,则这个菱形的面积为_______。 11.最简二次根式 ba 34  与 1 62 b ba 是同类二次根式，则 a b ＝ 。 12.已知：如图，ΔABC 中，AD 平分∠BAC,BD⊥AD 于 D, 点 E 的 BC 边的中点， AB=8,AC=12, 则 DE 长为____ __。 13．已知关于 x 的一元二次方程 014)1( 22  mxxm 有一个解是 0，则 m = 。 14.已知三角形两边长分别为 2 和 9,第三边的长为方程 x2-14 x+48=0 的一根, 则这个 三角形的周长为 。 15.实数 a、b、c 在数轴上表示如图，则 ||2 bca  = 。 16.如图，两名滑冰运动员陈洁和李莉分别在平坦冰面上的点 A 和点 B， 点 A 和 B 之间的距离是 100m,陈洁离开点 A 以 8m/s 的速度沿着与 AB 成 60°角的直线 滑行，在陈洁离开点的同时，李莉以 7m/s 的速度也沿着一条直线滑行离开点 B，这条 直线能使这两名滑冰者在给定的速度下最早相遇，则最早相遇的时间是 S。 三、解答题（共 10 题，共 102 分） 17. 计算或化简：（本题满分 16 分） E D B C A 第 12 题 第 16 题 （1） 18 50 3 8  （2） 32182 1324  （3） （ 4） 2 318 2 3 28a a a aa   18．解方程．（本题满分 16 分） （1） 0362 2  ）（x （2） 24 3 1 0x x   （3）2(x－3)²＝x²－9 （4） 24 8 1y y  （用配方法解） 19．（本题满 8 分）如图，在梯形 ABCD 中， AD BC AB DE AF DC E F∥ ， ∥ ， ∥ ， 、 两点在边 BC 上，且 AD=EF． （1） AD 与 BC 有何等量关系？请说明理由； （2）当 AB DC 时，求证：四边形 AEFD 是矩形． 2)23()25)(25(  A D CFEB 20．（本题满分 10 分）为了让广大青少年学生走向操场，走进自然，走到阳光下， 积极参加体育锻炼，我国启动了“全国亿万学生阳光体育运动”．短跑运动，可以锻炼人 的灵活性，增强人的爆发力，因此小明和小亮在课外活动中，报名参加了短跑训练小 组．在近几次百米训练中，所测成绩如图所示，请根据图中所示解答以下问题． (l) 请根据图中信息，补齐下面的表格： 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 小明 13.3 13.4 13.3 13.3 小亮 13.2 13.1 13.5 13.3 (2) 分别计算他们的平均数．极差和方差填入下表格，若你是他们的教练，将小明 与小亮的成绩比较后，你将分别给予他们怎样的建议？ 平均数 极差 方差 小明 小亮 21. （本题满分 6 分）已知:当 x=-2 时,二次三项式 2x2+mx+4 的值等于 18,当 x 为 何值时,这个二次三项式的值是 4 ? 22. （本题满 6 分）先阅读，后回答问题 X 为何值时 ( 1)x x  有意义？ 解：要使有意义需 ( 1)x x  ≥0 由乘法法则得 0 0 1 0 1 0 x x x x          或 解之得：X≥1 或 X≤0 即当X≥1 或 X≤0 时， ( 1)x x  有意义 ( 1)x x  体会解题思想后，解答，X 为何值是 2 2 1 x x   有意义？ 23．（本题满分 8 分） 2 2 2 2 1 2 11 2, a a aa a a a a       若 先化简再求 的值。 学 校 班 级 姓 名 考 试 号 … … … … … … … … … … … … … … … … 密 … … … … … … … … … … … … 封 … … … … … … … … … … … 线 … … … … … … … … … … … … … 24．（本题 10 分）如图，四边形 A BCD 中，E、F、G、H 分别是 AB、BC、CD、 DA的中点. （1）请判断四边形 EFGH 的形状？并说明为什么. （2）若使四边形 EFGH 为正方形，那么四边形 ABCD 的对角线应具有怎样的性质？ （3）在⑵的条件下，若 EF=2，求四边形 ABCD 的面 积。 25．（本题 10 分）数学课上，李老师出示了这样一道题目：如图1，正方形 ABCD 的边长为12 ，P 为边 BC 延长线上的一点，E 为 DP 的中点，DP 的垂直平分线交边 DC 于 M ，交边 AB 的延长线于 N .当 6CP  时， EM 与 EN 的比值是多少？ 经过思考，小明展示了一种正确的解题思路：过 E 作直线平行于 BC 交 DC ，AB 分 别于 F ，G ，如图 2 ，则可得： DF DE FC EP  ，因为 DE EP ，所以 DF FC .可求出 EF 和 EG 的值，进而可求得 EM 与 EN 的比值. (1) 请按照小明的思路写出求解过程. (2) 小东又对此题作了进一步探究，得出了 DP MN 的结论.你认为小东的这个结 论正确吗？如果正确，请给予证明；如果不正确，请说明理由. 26．（本题满分 12 分） 如图，已知矩形 ABCD 的边长 AB=3cm，BC＝6cm，某一时刻，动点 M 从点 A 出 发沿 AB 方向以1 /cm s 的速度向点 B 匀速运动；同时，动点 N 从点 D 沿 DA 方向以 2 /cm s 的速度向点 A 匀速运动. （1）经过多少时间，△AMN 的面积等于矩形 ABCD 面积的 9 1 ? (2) 是否存在时刻 t，使 A、M、N 为顶点的三角形与△ACD 相似？若存在，求 t 的值；若不存在，请说明理由. 第 25 题