2019-2020学年甘肃兰州九年级上数学期中试卷 12页

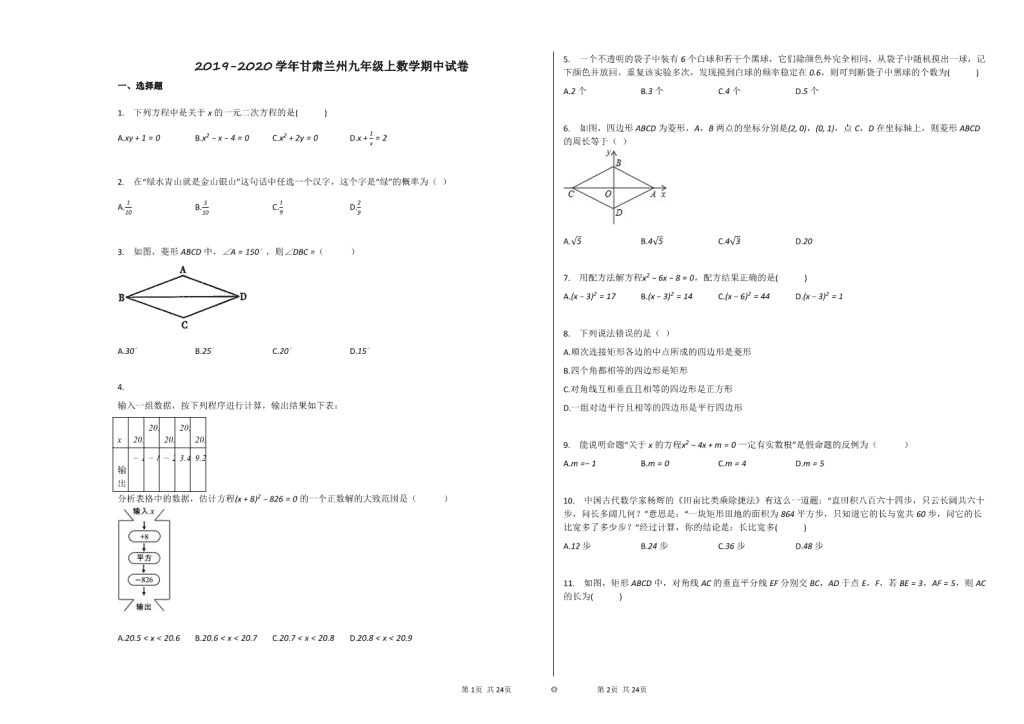
‎2019-2020学年甘肃兰州九年级上数学期中试卷 一、选择题 ‎ ‎ ‎1. 下列方程中是关于x的一元二次方程的是(        ) ‎ A.xy+1=0‎ B.x‎2‎‎−x−4=0‎ C.x‎2‎‎+2y=0‎ D.‎x+‎1‎x=2‎ ‎ ‎ ‎2. 在“绿水青山就是金山银山”这句话中任选一个汉字，这个字是“绿”的概率为（ ） ‎ A.‎1‎‎10‎ B.‎3‎‎10‎ C.‎1‎‎9‎ D.‎‎2‎‎9‎ ‎ ‎ ‎3. 如图，菱形ABCD中，‎∠A=‎‎150‎‎∘‎，则‎∠DBC=‎（        ） ‎ A.‎30‎‎∘‎ B.‎25‎‎∘‎ C.‎20‎‎∘‎ D.‎‎15‎‎∘‎ ‎ ‎ ‎4. ‎ 输入一组数据，按下列程序进行计算，输出结果如下表：‎ ‎ ‎x ‎ ‎‎20.5‎ ‎20.6‎ ‎ ‎‎20.7‎ ‎20.8‎ ‎ ‎‎20.9‎ ‎ 输出 ‎−13.75‎ ‎−8.04‎ ‎−2.31‎ ‎3.44‎ ‎9.21‎ 分析表格中的数据，估计方程‎(x+8‎)‎‎2‎−826=0‎的一个正数解的大致范围是（        ） ‎ A.‎20.560−x得x>30‎， 由题意得x(60−x)=864‎， 解得x=36‎或x=24‎（舍去）， 所以‎60−x=60−36=24‎， 所以长比宽多‎36−24=12‎(步). 故选A. ‎ ‎11.‎ ‎【答案】‎ B ‎【考点】‎ 全等三角形的性质与判定 矩形的性质 线段垂直平分线的性质 ‎【解析】‎ 连接AE，由线段垂直平分线的性质得出OA＝OC，AE＝CE，证明‎△AOF≅△COE得出AF＝CE＝‎5‎，得出AE＝CE＝‎5‎，BC＝BE+CE＝‎8‎，由勾股定理求出AB=AE‎2‎−BE‎2‎=4‎，再由勾股定理求出AC即可．‎ ‎【解答】‎ 解：连接AE，如图所示， ‎ 第21页 共24页 ◎ 第22页 共24页 ‎ ∵ EF是AC的垂直平分线， ∴ OA=‎OC，AE=‎CE， ∵ 四边形ABCD是矩形， ∴ ‎∠B=‎‎90‎‎∘‎，AD // BC， ∴ ‎∠OAF=‎‎∠OCE， 在‎△AOF和‎△COE中，‎∠AOF=∠COE，‎OA=OC，‎‎∠OAF=∠OCE，‎‎ ‎ ∴ ‎△AOF≅△COE(ASA)‎， ∴ AF=‎CE=‎‎5‎， ∴ AE=‎CE=‎‎5‎，BC=‎BE+CE=‎‎3+5‎＝‎8‎， ∴ AB=AE‎2‎−BE‎2‎=‎5‎‎2‎‎−‎‎3‎‎2‎=4‎， ∴ AC=AB‎2‎+BC‎2‎=‎4‎‎2‎‎+‎‎8‎‎2‎=4‎‎5‎. 故选B. 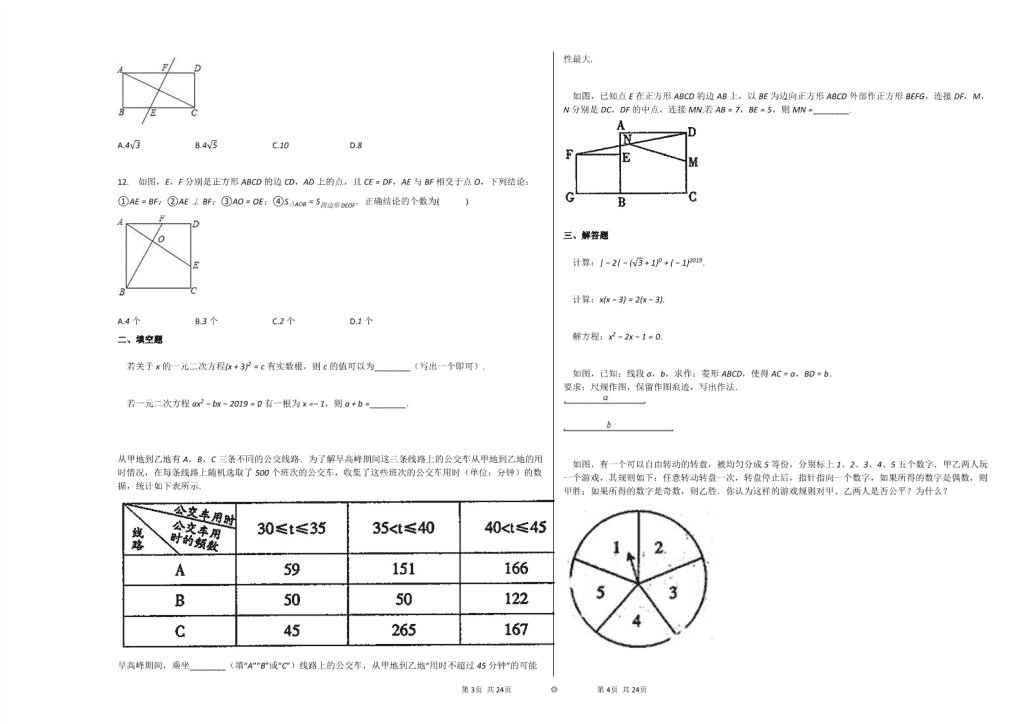‎ ‎12.‎ ‎【答案】‎ B ‎【考点】‎ 正方形的性质 全等三角形的性质 ‎【解析】‎ 首先利用全等三角形的判定方法利用SAS证明‎△BAF≅△ADE，即可得出AE=BF，进而得出‎∠BFA+∠EAD=‎‎90‎‎∘‎，即AE⊥BF，利用三角形全等即面积相等，都减去公共面积剩余部分仍然相等，即可得出D正确，过点E作EG⊥AB交BF与点H．然后依据直角三角形中斜边大于任何一条直角边进行判断即可．‎ ‎【解答】‎ 解：∵ 四边形ABCD是正方形， ∴ AB=AD，‎∠BAF=∠ADE=‎‎90‎‎∘‎． ∵ CE=DF， ∴ AF=DE． 在‎△ABF和‎△DAE中， AB=DA，‎‎∠BAF=∠ADE，‎AF=DE，‎ ∴ ‎△ABF≅△DAE， ∴ AE=BF，故①正确； ∵ ‎△ABF≅△DAE， ∴ ‎∠AFB=∠AED． ∵ ‎∠AED+∠DAE=‎‎90‎‎∘‎， ∴ ‎∠AFB+∠DAE=‎‎90‎‎∘‎， ∴ ‎∠AOF=‎‎90‎‎∘‎，即AE⊥BF，故②正确； ∵ ‎△ABF≅△DAE， ∴ S‎△ABF‎=‎S‎△ADE， ∴ S‎△AOB‎=S‎△ABF−‎S‎△AOF， S四边形DEOF‎=S‎△ADE−‎S‎△AOF， 即S‎△AOB‎=‎S四边形DEOF，故④正确； 如图，连接BE， 在‎△BCE中，BE‎2‎=BC‎2‎+CE‎2‎=AB‎2‎+CE‎2‎>AB‎2‎， ∴ BE>AB. 在‎△AOB和‎△BOE中， AO‎2‎=AB‎2‎−BO‎2‎, OE‎2‎=BE‎2‎−OB‎2‎， ∴ AO