北师大版数学九年级上册同步课件-1第一章-1菱形的性质与判定 21页

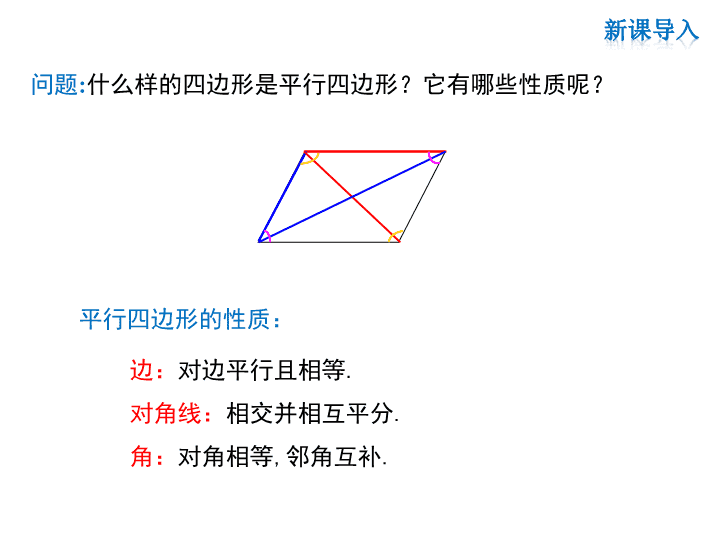
第一章 特殊平行四边形 1.1 菱形的性质与判定 第1课时 菱形的性质 1.了解菱形的概念及其与平行四边形的关系； 2.探索并证明菱形的性质定理.（重点） 3.应用菱形的性质定理解决相关问题.（难点） 学习目标 问题:什么样的四边形是平行四边形？它有哪些性质呢？ 平行四边形的性质： 边：对边平行且相等. 对角线：相交并相互平分. 角：对角相等,邻角互补. 活动: 观察下列图片， 找出你所熟悉的图形. 问题1: 观察上图中的这些平行四边形，你能发现它们有什么 样的共同特征？ 平行四边形 菱形 菱形：有一组邻边相等的平行四边形叫做菱形. 菱形的概念及其与平行四边形的关系1 菱形是特殊的平行四边形，它具有平行四边形的所 有性质，但平行四边形不一定是菱形. 问题2: 菱形与平行四边形有什么关系？ 归纳: 平行四边形 菱形 平行四边形 做一做 请同学们用菱形纸片折一折，回答下列问题： （1）菱形是轴对称图形吗？如果是，它有几条对称 轴？对称轴之间有什么位置关系？ （2）菱形中有哪些相等的线段？ 菱形的性质2 1.菱形是轴对称图形，有两条对称轴(对称轴为直线 AC和直线BD). 2.菱形四条边都相等(AB=BC=CD=AD). 3.菱形的对角线互相垂直(AC⊥BD). A B C O D 发现菱形的性质 已知：如图，在菱形ABCD中，AB=AD,对角线AC与BD相交 于点O. 求证:(1）AB = BC = CD =AD； （2）AC⊥BD. 证明菱形的性质 证明：（1）∵四边形ABCD是菱形， ∴AB = CD，AD = BC（菱形的对边相等）. 又∵AB=AD; ∴AB = BC = CD =AD. A B C O D 求证：菱形的四条边相等，对角线互相垂直. 思考：菱形的一条对角线所分成的两个内角有什么关系？ 试证明AC平分∠BAD和∠BCD， BD平分∠ABC和 ∠ADC. （2）∵AB=AD, ∴△ABD是等腰三角形. 又∵四边形ABCD是菱形， ∴OB=OD. 在等腰三角形ABD中， ∵OB=OD， ∴AO⊥BD， 即AC⊥BD. A B C O D 菱形是特殊的平行四边形，它除具有平行四边形的所有性 质外，还有平行四边形所没有的特殊性质. 对称性：是轴对称图形. 边：四条边都相等. 对角线：互相垂直. 角：对角相等，邻角互补. 边：对边平行且相等. 对角线：相交并相互平分. 1.如图，在菱形ABCD中，两条对角线 AC与BD相交于点O，图中的等腰三角 形有______________________________， 直角三角形有_____________________________ ，而且它们 ________（“全等”或“不全等”）. 抢答： 2.菱形具有而平行四边形不一定具有的性质是（ ） A.内角和为360° B.对角线互相垂直 C.对边平行 D.对角线互相平分 △ABD, △BCD，△ABC,△ADC △ABO，△ADO,△BCO,△CDO 全等 B B A C D O 4 cm 6 cm 归纳：菱形中已知边长或对角线，求相关长度问题，一般 利用菱形的对角线垂直平分，再结合勾股定理解题. 已知菱形ABCD中，对角线AC、BD相交于点 O，AB=5cm,BD=8cm. 则：（1）BO=____________; (2)AC=_____________. 例1 如图，在菱形ABCD中，对角线AC与BD相交于点O， ∠BAD=60°，BD =6，求菱形的边长AB和对角线AC的长. 解：∵四边形ABCD是菱形， ∴AC⊥BD(菱形的对角线互相垂直)， OB=OD= BD = ×6=3(菱形的对角线互相平分). 在等腰三角形ABC中， ∵∠BAD=60°， ∴△ABD是等边三角形. ∴AB = BD = 6. 1 2 1 2 A B C O D 例2 在RtΔAOB中，由勾股定理，得 OA2+OB2=AB2， ∴OA = = = ∴AC=2OA= （菱形的对角线相互平分）. 2 2AB O B 2 26 3 3 3. 6 3 A B C O D 归纳：若菱形有一个内角为60°，那么60°角的两边与较 短的对角线可构成等边三角形，且两条对角线把菱形分成 四个全等的含30°角的直角三角形. 1.菱形具有而一般平行四边形不具有的性质是 （ ） A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等 2.如图，菱形的两条对角线长分别是6和8，则此菱形的 周长是 （ ） A.40 B.32 C.24 D.20 C D 3.在菱形ABCD中，AE⊥BC，AF⊥CD，E、F分别 为BC，CD的中点，那么∠EAF的度数是 （ ） A.75° B.60° C.45° D.30° B FE C A B D 6.已知菱形的一条对角线与边长相等，则菱形的 四个内角度数分别为_____________________. 4.已知菱形的周长是12cm，那么它的边长是______. 5.菱形ABCD中∠ABC＝120 °，则∠BAC＝_______. A B C O D 3cm 30° 60°、60°、120°、120° 7.如图，在菱形ABCD中，对角线AC与BD 相交 于点O. 已知AB=5cm，AO=4cm，求BD的长. A B C O D 解：∵四边形ABCD是菱形， ∴AC⊥BD (菱形的两条对角线互相垂直), ∴∠AOB=90°, ∴BO= =3(cm), ∴BD=2BO=2×3=6(cm). 2 2AB AO 菱形的性质 菱形的性质 1.四边相等; 2.对角线互相垂直平分，且 每条对角线平分一组对角 菱形的定义 有一组邻边相等的平行四 边形是菱形