华师版九年级上册数学同步练习课件-期末复习2一元二次方程 28页

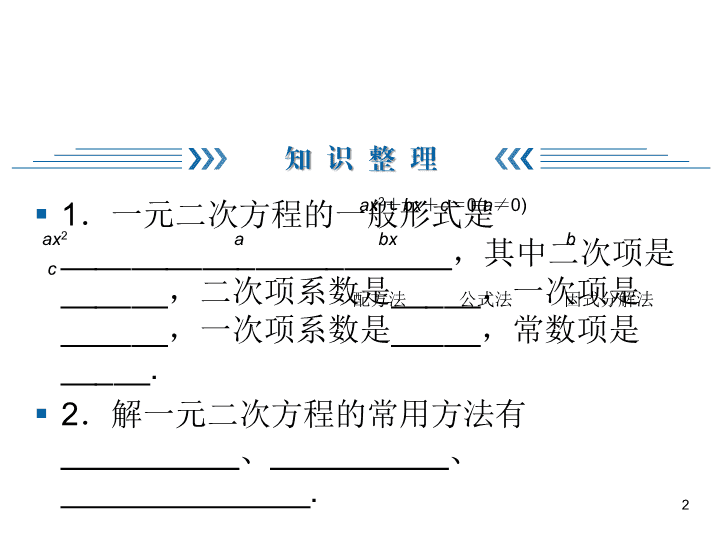
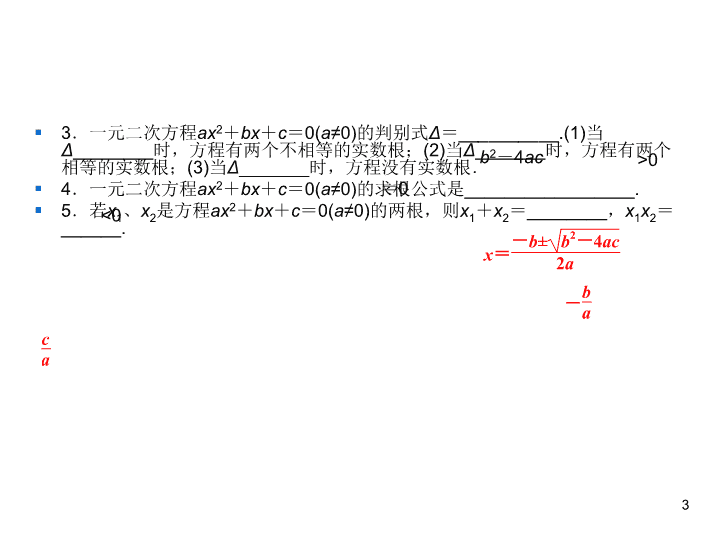
期末复习 期末复习2　一元二次方程 § 1．一元二次方程的一般形式是 ______________________，其中二次项是 ______，二次项系数是_____，一次项是 ______，一次项系数是_____，常数项是 _____. § 2．解一元二次方程的常用方法有 __________、__________、 ______________. 2 ax2＋bx＋c＝0(a≠0)　 ax2　 a　 bx　 b　 c　 配方法　 公式法　 因式分解法　 § 3．一元二次方程ax2＋bx＋c＝0(a≠0)的判别式Δ＝__________.(1)当 Δ________时，方程有两个不相等的实数根；(2)当Δ_______时，方程有两个 相等的实数根；(3)当Δ_______时，方程没有实数根． § 4．一元二次方程ax2＋bx＋c＝0(a≠0)的求根公式是_________________. § 5．若x1、x2是方程ax2＋bx＋c＝0(a≠0)的两根，则x1＋x2＝________，x1x2＝ ______. 3 b2－4ac　 >0　 ＝0　 <0　 § ★集训1　一元二次方程的解法 § 1．用直接开平方法解方程：(x－5)2＝16. § 解：方程两边开平方，得x－5＝±4，所以x1 ＝1，x2＝9. § 2．用配方法解方程：x2－4x＋1＝0. 4 § 3．用公式法解方程：2x(x＋4)＝1. 5 4．用适当的方法解方程：4x－6＝(3－2x)x. § 6．若关于x的方程x2－mx＋m＝0有两个相 等的实数根，则代数式2m2－8m＋1＝_____. 6 1　 § 7．已知关于x的一元二次方程x2＋3x－m＝0 有实数根． § (1)求m的取值范围； § (2)若两实数根分别为x1和x2，且x＋x＝11， 求m的值． 7 § 8．已知关于x的一元二次方程x2－2x－m＋1 ＝0. § (1)若x＝3是此方程的一个根，求m的值和它 的另一个根； § (2)若方程x2－2x－m＋1＝0有两个不相等的 实数根，试判断另一个关于x的一元二次方程 x2－(m－2)x＋1－2m＝0的根的情况． § 解：(1)∵x＝3是该方程的一个根，∴9－6－ m＋1＝0，解得m＝4，∴方程为x2－2x－3 ＝0，解得x1＝3，x2＝－1，即方程另一个根 为x＝－1. § (2)∵方程x2－2x－m＋1＝0有两个不相等的 实数根，∴Δ＞0，即(－2)2－4(－m＋1)＞0， 解得m＞0.∵方程x2－(m－2)x＋1－2m＝0 的判别式 Δ＝(m－2)2－4(1－2m)＝m2＋4m， ∴当m＞0时，m2＋4m＞0，∴方程有两个不 相等的实数根． 8 § ★集训3　一元二次方程的实际应用 § 9．某共享单车计划2017年10、11、12月连 续3月对深圳投放新型共享单车，计划10月 投放3000台，12月投放6000台，每月按相同 的增长率投放，设增长率为x，则可列方程 (　　) § A．3000(1＋x)2＝6000 § B．3000(1＋x)＋3000(1＋x)2＝6000 § C．3000(1－x)2＝6000 § D．3000＋3000(1＋x)＋3000(1＋x)2＝6000 9 A　 § 10．一次会议上，每两个参加会议的人都互 相握手一次，有人统计一共握了66次手，则 这次会议到会______人． § 11．某市要组织一次排球邀请赛，参赛的每 两个队之间都要比赛一场．根据场地和时间 等条件，赛程计划安排7天，每天安排4场比 赛，比赛组织者应邀请多少个队参赛？ § 解：∵赛程计划安排7天，每天安排4场比赛， ∴共7×4＝28(场)比赛．设比赛组织者应邀 请x个队参赛．由题意，得x(x－1)＝28×2， 解得x1＝8，x2＝－7(舍去). 即比赛组织者应 邀请8个队参赛． 10 12　 § 12．某商店从厂家以每件18元购进一批商品 出售，若每件售价为a元，则可售出(320－ 10a)件，但物价部门限定每件商品加价不能 超过进价的25%，若商店要想获得400元利 润，则售价应定为每件多少元？需售出这种 商品多少件？ § 解：设每件商品的售价定为a元，则(a－ 18)·(320－10a)＝400.整理，得a2－50a＋ 616＝0，解得a1＝22，a2＝28.∵18×(1＋ 25%)＝22.5，而28＞22.5，∴a＝22.故卖出 商品的件数为320－10×22＝100.即商店要 想获得400元利润，售价应定为每件22元， 需售出这种商品100件． 11 § 13．如图是一块长32 m、宽20 m的矩形实验 田，为了管理方便，准备沿平行于两边的方 向纵、横各开辟一条等宽的小道，要使种植 面积为540 m2，小道的宽应是多少米？ § 解：设小道的宽为x m．由题意，得(32－ x)(20－x)＝540.整理，得x2－52x＋100＝0. 解得x1＝2，x2＝50(不合题意，舍去)．故小 道的宽应是2 m. 12 § 一、选择题(每小题3分，共24分) § 1．某市2018年平均房价为每平方米8000元， 2020年平均房价降到每平方米7000元，设这 两年平均房价年平均降低率为x，根据题意， 下面所列方程正确的是 (　　) § A．8000(1＋x)2＝7000 B．8000(1－x)2＝ 7000 § C．7000(1－x)2＝8000 D．7000(1＋x)2＝ 8000 13 B　 § 2．若关于x的一元二次方程kx2＋2x－1＝0 有实数根，则实数k的取值范围是 (　　) § A．k≥－1 B．k＞－1 § C．k≥－1且k≠0 D．k＞－1且k≠0 § 3．一个等腰三角形的两条边长分别是方程x2 －7x＋10＝0的两根，则该等腰三角形的周 长是 (　　) § A．12 B．9 § C．13 D．12或9 § 4．一元二次方程x2－8x－1＝0配方后可变 形为 (　　) § A．(x＋4)2＝17 B．(x＋4)2＝15 § C．(x－4)2＝17 D．(x－4)2＝15 14 C　 A　 C　 15 D　 D　 16 D　 B　 § 二、填空题(每小题4分，共16分) § 9．将方程(x－3)2＋5＝6x化成一般形式是 _________________，其中一次项系数是 ________. § 10．已知关于x的一元二次方程x2＋(m＋3)x ＋m＋1＝0的两个实数根为x1、x2，若x＋x ＝4，则m的值为____________. § 11．关于x的方程mx2＋x－m＋1＝0，有以 下三个结论：①当m＝0时，方程只有一个实 数解；②当m≠0时，方程有两个不等的实数 解；③无论m取何值，方程都有一个负数解， 其中正确的是________.(填序号) 17 x2－12x＋14＝0　 －12　 －1或－3　 ①③　 § 12．某商场销售一批名牌衬衫，平均每天可 售出20件，每件可盈利40元．为了扩大销售 量，增加盈利，采取了降价措施，经调查发 现如果每件降价1元，那么商场平均每天可多 售出2件．若商场平均每天要盈利1200元， 并使每位顾客享受最大优惠，则每件衬衫应 降价______元． 18 20　 § 三、解答题(共60分) § 13．(16分)解下列方程： § (1)x2＋4x－5＝0； § 解：原方程变形，得(x－1)(x＋5)＝0，∴x－ 1＝0或x＋5＝0，∴x1＝1，x2＝ －5. § (2)x(x－4)＝2－8x； 19 § (3)x－3＝4(x－3)2； 20 (4)(x＋3)(x－1)＝12. 解：原方程变形为x2＋2x－15＝0.配方，得(x＋1)2＝16.∴x＋1＝±4，∴x1＝ 3，x2＝－5. 21 § 解：移项，得x2－2x＝24.配方，得x2－2x＋ 1＝24＋1，即(x－1)2＝25.开方，得x－1＝ ±5，解得x1＝6，x2＝－4. 22 四　 § 15．(8分)已知关于x的方程3x2－(a－3)x－a ＝0(a>0)． § (1)求证：方程总有两个不相等的实数根； § (2)若方程有一个根大于2，求a的取值范围． 23 § 16．(9分)2017年，某中学为了响应习总书记 “足球进校园”的号召，开设了“足球大课 间”活动，需要购进100个某品牌的足球供 学生使用，经调查，该品牌足球2015年单价 为200元，2017年单价为162元． § (1)求2015年到2017年该品牌足球单价平均 每年降低的百分率； § (2)在选购期间，发现该品牌足球在两个文体 用品商场有不同的促销方案，A商场的促销 方案是：买十送一；B商场的促销方案是： 全场九折，试问去哪个商场购买足球更优惠 24 25 § 17．(9分)关于x的一元二次方程x2＋(2k＋1)x＋k2＋1＝0有两个不等实 根x1、x2. § (1)求实数k的取值范围； § (2)若方程两实根x1、x2满足x1＋x2＝－x1·x2，求k的值． 26 27 28