- 249.42 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
HS九(上)
教学课件
第22章 一元二次方程
22.2 一元二次方程的解法
第5课时 一元二次方程的根与系数的关系
2.求根公式是什么?根的个数怎么确定的?
1.一元二次方程的解法有哪些,步骤呢?
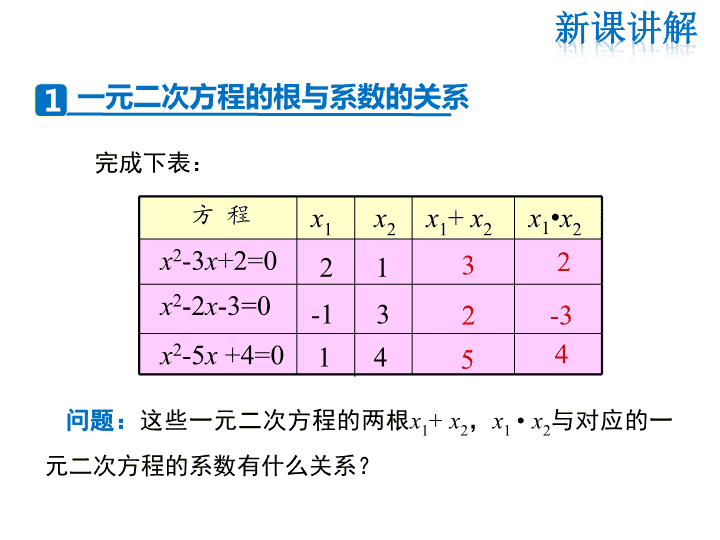
方 程 x1 x2 x1+ x2 x1•x2
x2-3x+2=0
x2-2x-3=0
x2-5x +4=0
问题:这些一元二次方程的两根x1+ x2,x1 • x2与对应的一
元二次方程的系数有什么关系?
2 1 3 2
-1 3 2 -3
1 4 5 4
一元二次方程的根与系数的关系1
完成下表:
由上可知,猜想正确!
猜想:当二次项系数为1时,方程 x2+px+q=0的两根为x1,x2,
那么
2 2
2 2
1 2
2 2
1 2
2 22 2
1 2
0 4 0 ,
4 4= = .2 2
4 4= =2 2
44 4= = .2 2 4
x px q p q
p p q p p qx x
p p q p p qx x p
p p qp p q p p qx x q
对于一元二次方程
由一元二次方程的求根公式,得到方程的两根分别为
,
所
验证
以 ,
:
+
猜想:
如果一元二次方程ax2+bx+c=0(a、b、c是常数,a≠0)
的两根为x1,x2,且
则x1+x2和x1•x2与系数a、b、c的关系为
2 4 0b ac ,
1 2x x
2 24 4
2 2
b b ac b b ac
a a
2 0( 0)ax bx c a
由一元二次方程的求根公式,得方程
的两根分别为
2 24 4
2
b b ac b b ac
a
2
2
b
a
b
a
,
2 2
1 2
4 4, .2 2
b b ac b b acx xa a
验证:
1 2x x 2 24 4
2 2
b b ac b b ac
a a
2 2 2
2
( ) ( 4 )
4
b b ac
a
2 2
2
( 4 )
4
b b ac
a
2
4
4
ac
a
.c
a
猜想正确!
任何一个一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1, x2,
那么 x1 + x2= , x1 ·x2=
注意:能用根与系数的关系的前提
条件为b2-4ac≥0.
韦达定理
一、直接运用根与系数的关系
不解方程,求下列方程两根之和两根之积.
2
2
2
(1) 6 15 0
(2)3 7 9 0
(3)5 1 4 .
x x
x x
x x
;
;
利用一元二次方程的根与系数的关系解决问题
1 2 1 21 6 15 x x , x x .解:
1 2 1 2
72 33
x x , x x .
1 2 1 2
5 13 4 4x x , x x .
2
在使用根与系数的关系
时,应注意:⑴不是一
般式的要先化成一般式;
⑵在使用x1+x2= 时,
注意“- ”不要漏写.
例1
二、求关于两根的代数式的值
2 2
1 2(1)x x ;
1 2
1 1(2) x x
;
设 是方程 的两个根,利用根与系
数的关系,求下列各式的值.
21 , xx 0342 2 xx
1 2(3)( 1)( 1)x x ; 2 2
1 2 1 2(4)x x x x ;
2 1
1 2
(5) x x
x x
; 2
1 2(6)( ) .x x
例2
1 2 1 2
32 2
x x , x x .
2 22 2
1 2 1 2 1 2
1 2
1 2 1 2
1 2 1 2 1 2
2 2
1 2 1 2 1 2 1 2
2 2
2 1 1 2
1 2 1 2
2 2 2
1 2 1 2 1
31 2 2 2 72
1 1 2 42 3 3
2
3 53 1 1 1 2 12 2
34 2 32
7 145 3 3
2
6 2
x x x x x x .
x x .x x x x
x x x x x x .
x x x x x x x x .
x x x x .x x x x
x x x x x 2 7 3 10 x .
解:由题意知
三、构造新方程
求一个一元二次方程,使它的两个根是2和3,且二次
项系数为1.
解:(x-2)(x-3)=0,
即x2-5x+6=0.(答案不唯一)
例3
方程 的两根之和为6,一根为2,求p、
q的值.
02 qpxx
四、求方程中的待定系数
解:设方程的另一个根为x1.
由题意,得
2+x1=-p=6,2x1=q,
所以x1=4,p=-6,q=8.
例4
1.方程 有一个正根,一个负根,
求m的取值范围.
解:根据题意,得
∴00,
0