华师版九年级上册数学同步练习课件-第25章 随机事件的概率-25频率与概率(第二课时) 18页

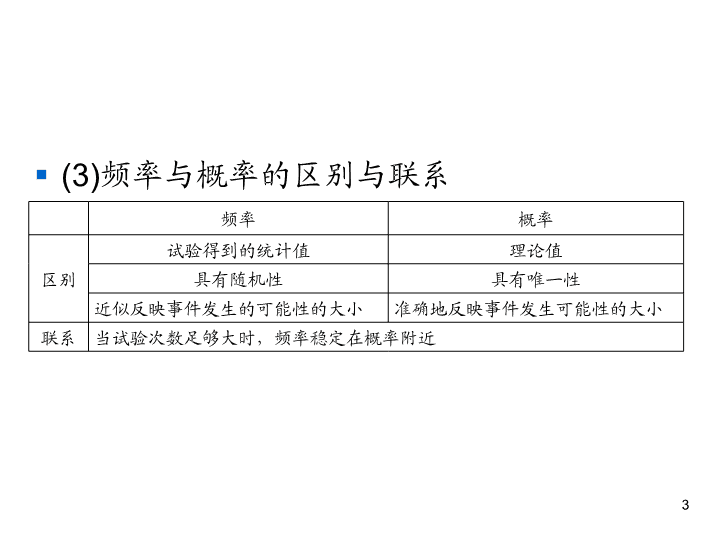
第25章　随机事件的概率 25.2　随机事件的概率 2　频率与概率(第二课时) § 知识点1　用频率估计概率 § (1)一般地，在大量重复试验中，如果事件A 发生的频率会稳定在某个常数附近，那么这 个常数就叫做事件A的概率． § 注意：(1)通过重复试验用频率估计概率时， 必须要求试验是在相同条件下进行的．(2)在 相同条件下，试验次数越多，就越有可能得 到更好的估计值，但不同小组试验所得的估 计值也不一定相同． 2 § (3)频率与概率的区别与联系 3 频率 概率 区别 试验得到的统计值 理论值 具有随机性 具有唯一性 近似反映事件发生的可能性的大小 准确地反映事件发生可能性的大小 联系 当试验次数足够大时，频率稳定在概率附近 § 【典例1】一个不透明的口袋里装有若干除颜 色外其他完全相同的小球，其中有6个黄球， 将口袋中的球摇匀，从中任意摸出一个球记 下颜色后再放回，通过大量重复上述试验后 发现，摸到黄球的频率稳定在30%，由此估 计口袋中共有小球______个． § 分析：∵摸到黄球的频率稳定在30%， § ∴在大量重复上述试验下，可估计摸到黄球 的概率为30%＝0.3. § 又∵袋中黄球只有6个， § ∴估计袋中小球大约有6÷0.3＝20(个)． § 答案：20 4 § 知识点2　转盘游戏 § 在转盘游戏中，从表面上看是扇形的面积决 定了指向某个扇形的概率，但在本质上是由 扇形所在的圆心角的度数决定概率的大小 的． 5 § 【典例2】“六一”儿童节期间，某商厦为了 吸引顾客，设立了一个可以自由转动的转盘 (转盘被平均分成16份)，并规定：顾客每购 买100元的商品，就能获得一次转动转盘的 机会．如果转盘停止后，指针正好对准哪个 区域，顾客就可以获得相应的奖品. 6 颜色 奖品 红色 玩具熊 黄色 童话书 绿色 彩笔 小明和妈妈购买了125元的商品，请你分析计算： (1)小明获得奖品的概率是多少？ (2)小明获得童话书的概率是多少？ § 分析：(1)看有颜色部分的份数占总份数的几 分之几即为所求的概率；(2)看黄色部分的份 数占总份数的几分之几即为所求的概率． 7 点评：本题将概率的求解设置于转动转盘游戏中，考查学生对简单几何概率 的掌握情况． § 1．大量重复试验中，关于随机事件发生的频 率和概率，下列说法正确的是 (　　) § A．频率就是概率 § B．频率与试验次数无关 § C．在相同的条件下进行试验，如果试验次 数相同，则各实验小组所得频率的值也会相 同 § D．随着试验次数的增加，频率一般会逐步 稳定在概率数值附近 8 D　 9 D　 § 3．在一个不透明的口袋中，装有若干个红球和4个黄球，它们除 颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后 再放回口袋中．通过大量重复摸球试验发现，摸到黄球的频率是 0.2，则估计盒子中大约有红球 (　　) § A．16个 B．20个 § C．25个 D．30个 10 A　 11 A　 12 0.881　 § 6．如图，为测量平地上一块不规则区域(图 中的阴影部分)的面积，画一个边长为2 m的 正方形，使不规则区域落在正方形内，现向 正方形内随机投掷小石子(假设小石子落在正 方形内每一点都是等可能的)，经过大量重复 投掷试验，发现小石子落在不规则区域的频 率稳定在常数0.25附近，由此可估计不规则 区域的面积是_____ m2. 13 1　 14 7　 § 9．“2018东台西溪半程马拉松”的赛事共 有两项：A、“半程马拉松”、B、“欢乐 跑”．小明参加了该项赛事的志愿者服务工 作，组委会随机将志愿者分配到两个项目 组． § (1)小明被分配到“半程马拉松”项目组的概 率为______； § (2)为估算本次赛事参加“半程马拉松”的人 数，小明对部分参赛选手作如下调查： 15 调查总人数 20 50 100 200 500 参加“半程马拉松”人数 15 33 72 139 356 参加“半程马拉松”频率 0.750 0.660 0.720 0.695 0.712 § ①请估算本次赛事参加“半程马拉松”人数的概率为 _______； (精确到0.1) § ②若本次参赛选手大约有3000人，请你估计参加“半程马拉松” 的人数是多少？ § 解：参加“半程马拉松”的人数是3000×0.7＝2100(人)． 16 0.7　 17 18