华师版数学九年级上册课件-第24章-24 直角三角形的性质 13页

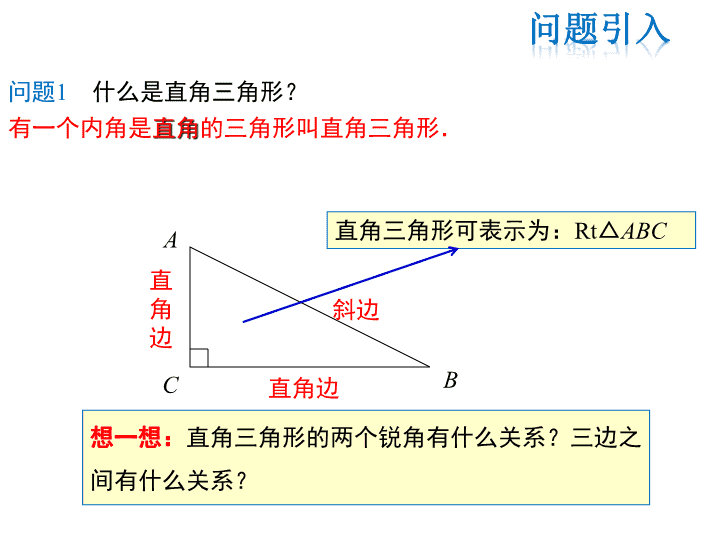
第24章 解直角三角形 24.2 直角三角形的性质 直角三角形可表示为：Rt△ABCA C B 斜边 直角边 直 角 边 想一想：直角三角形的两个锐角有什么关系？三边之 间有什么关系？ （1）直角三角形的两个锐角_________；互余 （2）勾股定理：直角三角形两直角边的平方和______斜边的 平方. 等于 下面我们探索直角三角形的其 他性质. 问题2 你知道我们学过了直角三角形的哪些性质？ 1. 在Rt△ABC中，两锐角的和∠A＋∠B=？ ∠A＋∠B=90° 2. 在△ABC中，如果∠A＋∠B= 90º ，那么△ABC是直角三角形吗？ 是 3. 在Rt△ABC中，AB、AC、BC之间 有什么关系？ AB2=AC2+BC2 A B C 直角三角形斜边上的中线等于斜边上的一半 问题引导 1 任意画一个直角三角形，作出斜边上的中线，并利用圆规比较 中线与斜边的一半的长短，你发现了什么？再画几个直角三角 形试一试，你的发现相同吗？ 我们来验证一下！ A B C D 探究归纳 直角三角形的性质之一 ★在直角三角形中，斜边上的中线等于斜边的一半. 数学语言表述为： 在Rt△ABC中 ∵CD是斜边AB上的中线, ∴CD＝AD＝BD＝ AB. （直角三角形斜边上的中线等于斜边的一半) 1 2 A B C ∟ D 证明： 思路引导：中线辅助线作法：将中线延长一倍. 延长CD到点E，使DE=CD，连结AE、BE. E∵ CD是斜边AB的中线， ∴ AD=BD. 又∵ DE=CD， ∴ 四边形ACBE是平行四边形. 又∵∠ACB=90⁰ ， ∴ ACBE是矩形， ∴ CE=AB. 如图，Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线. 求证：CD= AB. 1 2 1 1 2 2 CD CE AB  例1 CB D 练一练 Rt△ABC中，∠ACB=90 ° ，∠A=30°，求证：BC= AB. 证明： 作斜边上的中线CD， 则CD=AD=BD= AB. （在直角三角形中，斜边上的中线等于斜边的一半） ∵ ∠A=30° ∴ ∠B=60° ∴ △CDB是等边三角形， ∴ BC=BD= AB. 1 2 CB A D 直角三角形中，30°角所对的直角边等于斜边的一半2 例2 1.如图，在△ABC中，若∠BAC=120°，AB=AC, AD⊥AC于 点A，BD=3，则BC=______. D C A B 9 2.如图， ∠C=90°，∠B=15°，DE垂直平分AB，垂足为点E， 交BC边于点D,BD=16cm，则AC的长为______. E D C A B 8cm 3.如图，在△ABC中，BD、CE是高，M、N分别是BC、ED的 中点，试说明：MN⊥DE. 解：连结EM、DM. ∵BD、CE是高，M是BC中点， ∴在Rt△BCE和Rt△BCD中， ∴EM=DM. 又∵N是ED的中点， ∴MN⊥ED 性质1 直角三角形两个锐角互余 性质2 直角三角形的勾股定理 性质3 直角三角形斜边上的中线等于斜 边的一半 性质4 直角三角形30⁰ 角所对直角边等 于斜边的一半