华东师大版数学中考专题复习与训练课件-第1篇 第6章 6多边形与圆 49页

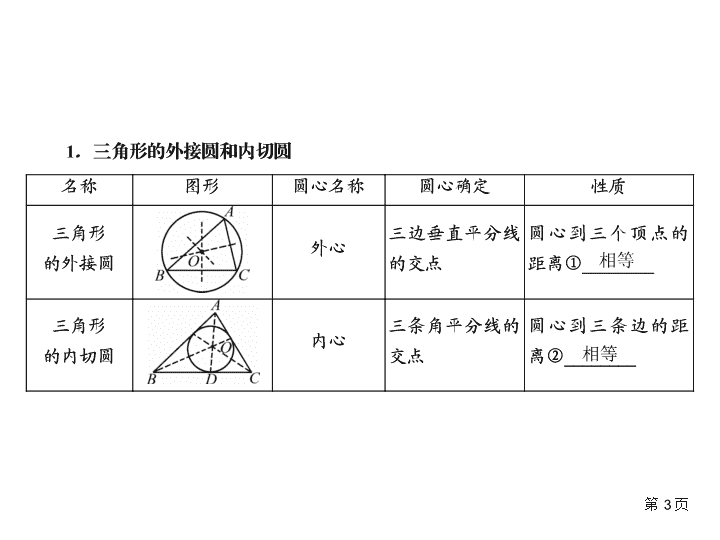
第一篇 过教材·考点透析 第六章　圆 6.3　多边形与圆 第 2 页 第 3 页 相等　 相等　 第 4 页 第 5 页 方法点拨：已知三角形的内心，作辅助线的常用方法：(1)过三角形的内心作 三边的垂线段；(2)连结内心和三角形的顶点． 易错提示：(1)三角形的外接圆的圆心可能在三角形内部、外部、三角形上； (2)三角形的内切圆的圆心只能在三角形的内部． 第 6 页 外接　 互补　 180°　 等于　 ∠A　 § 3．正多边形和圆 § (1)正多边形的外接圆：把圆分为n(n≥3)等份，依次连结各分点所 得的多边形就是这个圆的内接正n边形，这个圆也就是正n边形的 外接圆． § (2)正多边形的内切圆：把圆分为m(m≥3)等份，经过各分点作圆 的切线，以相邻切线的交点为顶点的多边形就是这个圆的外切正 m边形，这个圆也就是正m边形的内切圆． § (3)任何一个正多边形都有一个外接圆和一个内切圆，且它们是同 心圆． § (4)一个正多边形的外接圆的圆心叫做这个正多边形的中心，外接 圆的半径叫做正多边形的⑨________，正多边形每一边所对的圆 心角叫做正多边形的中心角，中心到正多边形每一边的距离叫做 正多边形的⑩__________. 第 7 页 半径　 边心距　 第 8 页 方法点拨：(1)正多边形中心与正多边形顶点连线的长度等于外接圆半径；(2) 外接圆半径、边心距(正多边形中心与边的距离)、正多边形一边的一半，刚好构成 一个直角三角形． § 命题点一　三角形的内切圆和外接圆 § 1．(2017·眉山中考)如图，在△ABC中， ∠A＝66°，点I是内心，则∠BIC的大小为 (　　) § A．114°　 § B．122°　 § C．123°　 § D．132° 第 9 页 C　 § 2．(2018·凉山中考)如图，△ABC外接圆的 圆心坐标是__________. 第 10 页 (4,6)　 § 命题点二　圆内接四边形的性质 § 4．(2017·凉山中考)如图，已知四边形 ABCD内接于半径为4的⊙ O中，且∠C＝ 2∠A，则BD＝_______. 第 11 页 第 12 页 A　 第 13 页 B　 第 14 页 C　 § 8．(2019·广安中考)如图，正五边形ABCDE 中，对角线AC与BE相交于点F，则∠AFE＝ ______度． 第 15 页 72　 § 核心素养 § 9．(2019·湖北孝感中考)刘徽是我国魏晋时 期卓越的数学家，他在《九章算术》中提出 了“割圆术”，利用圆的内接正多边形逐步 逼近圆来近似计算圆的面积．如图，若用圆 的内接十二边形的面积S1来近似估计⊙O的 面积S，设⊙O的半径为1，则S－S1＝ ________. 第 16 页 0.14　 第 17 页 第 18 页 第 19 页 R－d　 第 20 页 § 突破点一　圆内接四边形的性质 § 　　　(2019·山东德州中考)如图，点O为线 段BC的中点，点A、C、D到点O的距离相等， 若∠ABC＝40°，则∠ADC的度数是 (　　) § A．130°　 B．140°　 § C．150°　 D．160° 第 21 页 B　 § 思路分析：由题意，得OA＝OB＝OC＝ OD．以O为圆心，作出如图所示的圆，则四 边形ABCD为⊙O的内接四边形，∴∠ABC ＋∠ADC＝180°.∵∠ABC＝40°， ∴∠ADC＝140°. § 解题技巧：圆内接四边形的对角互补及圆内 接四边形的一个外角等于它的内对角是解决 圆的有关计算与证明中的“桥梁”． 第 22 页 第 23 页 D　 § 解题技巧：关于正多边形和圆主要掌握其中的中心角、边心距、面积、 周长的计算公式，熟练掌握正六边形的性质，由三角函数求出OC是解 题的关键． 第 24 页 第 25 页 A　 § 解题技巧：三角形的内心到三角形三边的距离相等；三角形的内心与三 角形顶点的连线平分这个内角．解答此题的关键是学会添加辅助线，构 造直角三角形． 第 26 页 § 　　　(湖南长沙中考)如图，在△ABC中， AD是边BC上的中线，∠BAD＝∠CAD， CE∥AD，CE交BA的延长线于点E，BC＝8， AD＝3. § (1)求CE的长； § (2)求证：△ABC为等腰三角形； § (3)求△ABC的外接圆圆心P与内切圆圆心Q 之间的距离． 第 27 页 § 自主解答：(1)解：∵AD是边BC上的中线，∴BD＝ CD．∵CE∥AD，∴AD为△BCE的中位线，∴CE＝2AD＝6. § (2)证明：∵CE∥AD，∴∠BAD＝∠E，∠CAD＝ ∠ACE.∵∠BAD＝∠CAD，∴∠ACE＝∠E，∴AE＝AC．∵AB＝AE，∴AB＝AC，∴△ABC为等腰三角形. 第 28 页 第 29 页 § 解题技巧：本题考查了三角形内切圆与内心： 三角形的内心到三角形三边的距离相等；三 角形的内心与三角形顶点的连线平分这个内 角．也考查了等腰三角形的判定与性质和三 角形的外接圆． 第 30 页 § 1．(2019·浙江湖州中考)如图，已知正五边 形ABCDE内接于⊙ O，连结BD，则∠ABD 的度数是 (　　) § A．60°　 § B．70°　 § C．72°　 § D．114° 第 31 页 A 双基过关 C　 § 2．(河北中考)如图，点I为△ABC的内心， AB＝4，AC＝3，BC＝2，将∠ACB平移使 其顶点与I重合，则图中阴影部分的周长为 (　　) § A．4.5　 § B．4　 § C．3　 § D．2 § 3．(内蒙古呼和浩特中考)同一个圆的内接正 方形和正三角形的边心距的比为 _________． 第 32 页 B　 § 4．(湖南株洲中考)如图，正五边形ABCDE 和正三角形AMN都是⊙ O的内接多边形，则 ∠BOM＝________． 第 33 页 48°　 § 5．(浙江湖州中考)如图，已知△ABC的内切 圆⊙ O与BC边相切于点D，连结OB、 OD．若∠ABC＝40°，则∠BOD的度数是 ________． 第 34 页 70°　 § 6．(山东威海中考)如图，在扇形CAB中， CD⊥AB，垂足为点D，⊙ E是△ACD的内切 圆，连结AE、BE，则∠AEB的度数为 _________． 第 35 页 135°　 § 7．(四川宜宾中考)如图，⊙ O的内接正五边 形ABCDE的对角线AD与BE相交于点G，AE ＝2，则EG的长是_________． 第 36 页 第 37 页 第 38 页 第 39 页 第 40 页 第 41 页 B 满分过关 D　 § 11．(四川泸州中考)如图，在平面直角坐标 系中，已知点A(1,0)、B(1－a,0)、C(1＋ a,0)(a＞0)，点P在以D(4,4)为圆心，1为半径 的圆上运动，且始终满足∠BPC＝90°，则 a的最大值是_____． 第 42 页 6　 第 43 页 8　 第 44 页 第 45 页 § 问题：如图，在△ABC中，AB＝ 13，BC＝12，AC＝7，⊙ O内切 于△ABC，切点分别是D、E、 F． § (1)求△ABC的面积； § (2)求⊙ O的半径． 第 46 页 § 14．(2019·内蒙古呼和浩特中考)如 图，以Rt△ABC的直角边AB为直径 的⊙ O交斜边AC于点D，过点D作 ⊙ O的切线交BC于点E，弦DM与 AB垂直，垂足为H． § (1)求证：E为BC的中点； 第 47 页 (2)若⊙ O的面积为12π，两个三角形△AHD和△BMH的外接圆面积之比为3， 求△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比． § (1)证明：如图，连结BD、OE.∵AB是直径， 则∠ADB＝∠ADO＋∠ODB＝90°， ∴∠CAB＋∠ABD＝90°.∵DE是切线， ∴∠ODE＝∠EDB＋∠ODB＝90°， ∴∠EDB＝∠ADO＝∠CAB．∵∠ABC＝ ∠ABD＋∠DBC＝90°，∴∠DBC＝∠CAB， ∴∠EDB＝∠EBD．又∵∠BDC＝90°， ∴E为BC的中点． 第 48 页 第 49 页