华师版九年级上册数学同步课件-第22章-22一元二次方程的解法 13页

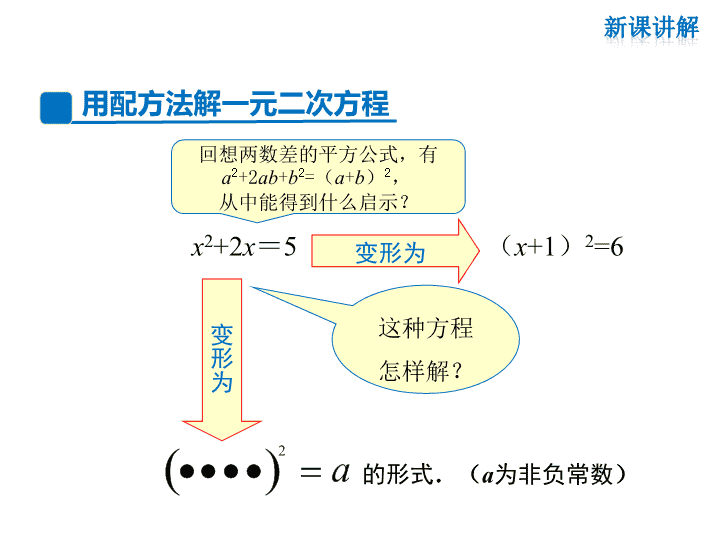
第22章 一元二次方程 22.2 一元二次方程的解法 第2课时 配方法 读诗词解题： （通过列方程，算出周瑜去世时的年龄） 大江东去浪淘尽，千古风流数人物. 而立之年督东吴，早逝英年两位数. 十位恰小个位三，个位平方与寿符. 哪位学子算得快，多少年华属周瑜？ 解：设个位数字为x，则十位数字为x-3. 整理，得x2-11x+30=0. 根据题意，得x2=10(x-3)+x. ？思考 怎样求解？ 这种方程 怎样解？ 变 形 为  2 a  的形式．（a为非负常数） 变形为x2+2x＝5 （x+1）2=6 用配方法解一元二次方程 回想两数差的平方公式，有 a2+2ab+b2=（a+b）2， 从中能得到什么启示？ 归纳： 像这样，通过方程的简单变形，将左边配成一个 含有未知数的完全平方式，右边是一个非负常数，从而可以 直接开平方求解.这种解一元二次方程的方法叫做配方法. 解方程：x2+2x＝5. 解：原方程两边都加上1，得x2+2x+1=6， 即（x+1）2=6. 直接开平方，得x+1= 所以x=-1± ， 即x1=-1+ ，x2=-1- . 6. 6 6 6 例题 (1)x2＋8x＋ =(x＋4)2 (2)x2－4x＋ =(x－ )2 (3)x2－___x＋ 9 =(x－ )2 归纳： 配方时， 等式两边同时加上的是 的平方. 16 6 3 4 2 探究 用配方法解一元二次方程的一般步骤: 化1： 把二次项系数化为1； 移项：把常数项移到方程的右边； 配方：方程两边都加上一次项系数一半的平方； 变形：将方程化成（x+m）2=a(a≥0)的形式； 开方：根据平方根意义，方程两边开平方； 求解：解一元一次方程； 定解：写出原方程的解. ★ (2) -x2＋4x-3=0.(1) x2＋12x =-9； 1.用配方法解下列方程： 解：(1) 配方（两边同时加上36），得 x2＋2•x•6+62=-9+62，即（x+6）2=27. 直接开平方，得x+6= ， 所以 （2）原方程可化为x2-4x+3=0. 配方，得（x-1）（x-3)=0， 所以 x1=1，x2=3. 1 26 3 3 6 3 3     x , x . 3 3 2.用配方法说明：不论k取何实数，多项式k2-3k＋5的值必 定大于零. 证明： k2-3k＋5=(k- )2+ . ∵ (k- )2≥0， ∴ k2-3k＋5＞0. 即不论k取何实数，多项式k2-3k＋5 的值必定大于零. 3 2 11 4 3 2 3.先用配方法解下列方程： （1） x2-2x-1＝0； （2） x2-2x+4＝0； （3） x2-2x+1＝0； 然后回答下列问题： （4）你在求解过程中遇到什么问题？你是怎样处理所遇到 的问题的？ （5）对于形如x2+px+q＝0这样的方程，在什么条件下才有 实数根？ 解：(1) 左右两边同时加2，得x2-2x+1=2. 配方，得（x-1）2=2，解得 （2）左右两边同时减去3，得x2-2x+1=-3. 配方，得(x-1)2=-3，显然此方程无解. （3）原方程配方，得(x-1)2=0，解得x=1. （4）略 （5） 1 21 2 1 2   x , x . 2 2 2 2 2 2 0 2 4 0 2 4 4 0                          p px px q x q , p px q , p q . 即当p2-4q≥0时，形如x2+px+q＝0这样的方程，才有实数根. 通过方程的简单变形，将左边配成一个含有未知数的完 全平方式，右边是一个非负常数，从而可以直接开平方求解. 这种解一元二次方程的方法叫做配方法. ★配方法 用配方法解一元二次方程的一般步骤： 1.化1： 把二次项系数化为1； 2.移项：把常数项移到方程的右边； 3.配方：方程两边都加上一次项系数一半的平方； 4.变形：将方程化成（x+m）2=a(a≥0)的形式； 5.开方：根据平方根意义，方程两边开平方； 6.求解：解一元一次方程； 7.定解：写出原方程的解. ★