2017-2018学年四川省南充市营山县九年级上数学期末试卷(含答案) 12页

2017--2018 学年上学期九年级数学期末质量检测 （考试时间：120 分 总分 120 分） ______学校 年级 班______ 姓名 考号________成绩 一.选择题（每小题 3 分，共 30 分） 1、方程 的左边配成完全平方后，得到的方程为（ ）. A． B． C． D．以上都不对 2、在一幅长 80cm，宽 50cm 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如 果要使整个挂图的面积是 5400cm2，设金色纸边的宽为 ，则 满足的方程是（ ） A. B. C. D. 3、如图，在 Rt△ABC 中，∠BAC=90°，∠B=60°，△ADE 可以由△ABC 绕点 A 顺时针旋转 900 得到，点 D 与点 B 是对应点，点 E 与点 C 是对应点)，连接 CE，则∠CED 的度数是( ) （A）45° （B）30° （C）25° （D）15° 4、下列图形中，是中心对称图形的是（ ） 5、如图，A,B,C 是⊙O 上三个点,∠AOB=2∠BOC,则下列说法中正确的是 A. ∠OBA=∠OCA B. 四边形 OABC 内接于⊙O C.. AB=2BC D. 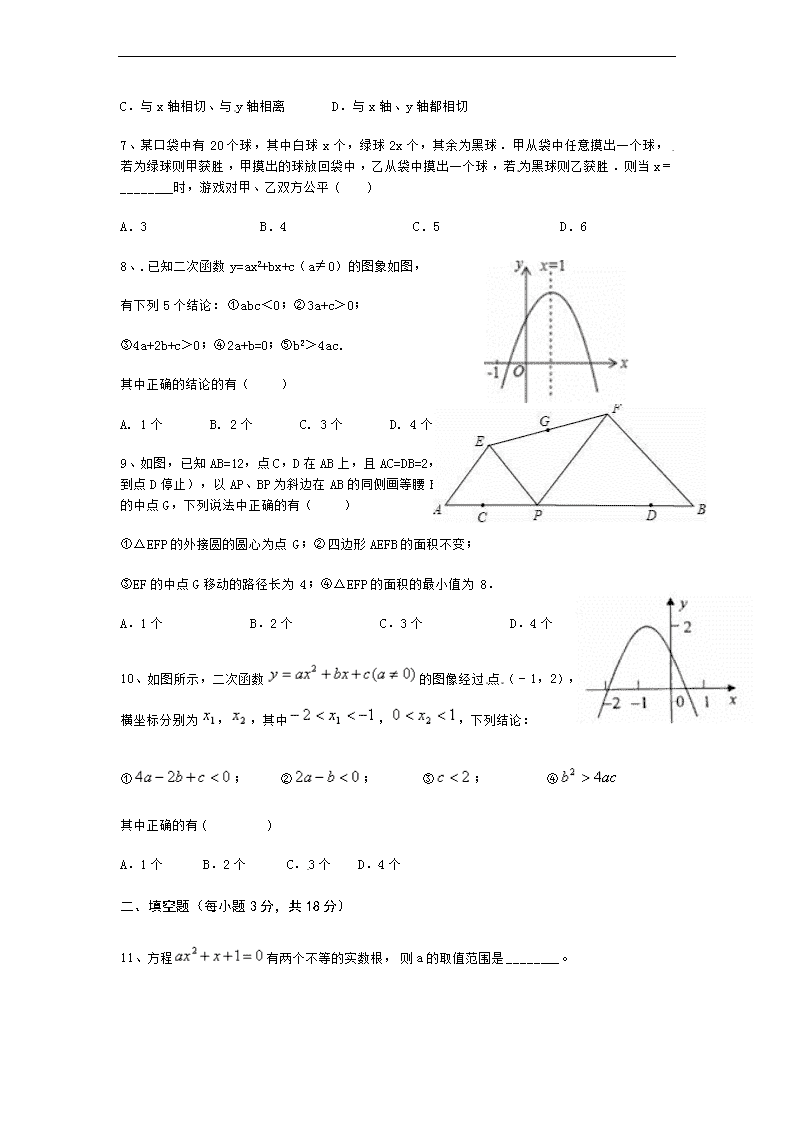∠OBA+∠BOC=90° 6、在平面直角坐标系中，以点（3，2）为圆心，2 为半径的圆与坐标轴的位置关系为（ ） A．与 x 轴相离、与 y 轴相切 B．与 x 轴、y 轴都相离 C．与 x 轴相切、与 y 轴相离 D．与 x 轴、y 轴都相切 7、某口袋中有 20 个球，其中白球 x 个，绿球 2x 个，其余为黑球．甲从袋中任意摸出一个球， 若为绿球则甲获胜，甲摸出的球放回袋中，乙从袋中摸出一个球，若为黑球则乙获胜．则当 x ＝________时，游戏对甲、乙双方公平( ) A．3 B．4 C．5 D．6 8、.已知二次函数 y=ax2+bx+c（a≠0）的图象如图， 有下列 5 个结论：①abc＜0；②3a+c＞0； ③4a+2b+c＞0；④2a+b=0；⑤b2＞4ac. 其中正确的结论的有（ ） A. 1 个 B. 2 个 C. 3 个 D. 4 个 9、如图，已知 AB=12，点 C，D 在 AB 上，且 AC=DB=2，点 P 从点 C 沿线段 CD 向点 D 运动（运动 到点 D 停止），以 AP、BP 为斜边在 AB 的同侧画等腰 Rt△APE 和等腰 Rt△PBF，连接 EF，取 EF 的中点 G，下列说法中正确的有（ ）www-2-1-cnjy-com ①△EFP 的外接圆的圆心为点 G；②四边形 AEFB 的面积不变； ③EF 的中点 G 移动的路径长为 4；④△EFP 的面积的最小值为 8． A．1 个 B．2 个 C．3 个 D．4 个 10、如图所示，二次函数 的图像经过点 （－1，2），且与 轴交点的 横坐标分别为 ， ，其中 ， ，下列结论： ① ； ② ； ③ ； ④ 其中正确的有( ) A．1 个 B．2 个 C．3 个 D．4 个 二、填空题（每小题 3 分，共 18 分） 11、方程 有两个不等的实数根，则 a 的取值范围是________。 12、如图，⊙O 中，弦 AB=3，半径 BO= ，C 是 AB 上一点且 AC=1， 点 P 是⊙O 上一动点，连 PC，则 PC 长的最小值是 13.将一批数据分成 5 组，列出频率分布表，其中第一组与第五组的概 率之和是 0.2，第二与第四组的概率之和是 0.25，那么第三组的概率是 ． 14、挂钟分针的长 10cm，经过 45 分钟，它的针尖转过的弧长是 cm． 15、15、在平面直角坐标系中，二次函数 与一次函数 的 图像交于 A、B 两点，已知 B 点的横坐标为 2，当 时，自变量 的取值范围是 ． 16、在平面直角坐标系中，将抛物线 C1：y=x2 绕点（1，0）旋转 180°后，得到抛物线 C2，定义 抛物线 C1 和 C2 上位于﹣2≤x≤2 范围内的部分为图象 C3．若一次函数 y=kx+k﹣1（k＞0）的图象 与图象 C3 有两个交点，则 k 的范围是： ． 三、解答题（17、18、19 题各 6 分，20、21、22 题各 8 分，23、24、25 题各 10 分，共 72 分） 17、 解方程：(x－3)(x－1)＝3. 18、如图，正方形网格中，△ABC 为格点三角形（顶点都是格点），将△ABC 绕点 A 按逆时针方 向旋转 90°得到 ．2 （1）在正方形网格中，作出 ；（不要求写作法） （2）设网格小正方形的边长为 1cm，用阴影表示出旋转过程中线段 BC 所扫过的图形，然后求 出它的面积．（结果保留 ） 19、课前预习是学习的重要缓解，为了了解所教班级学生完成课前预习的具体情况，某班主任对 本班部分学生进行了为期半个月的跟踪调查，他将调查结果分为四类：A．优秀，B．良好，C．一 般 ，D．较差，并将调查结果绘制成以下两幅不完整的统计图． （1）本次调查的样本容量是 ；其中 A 类女生有 名，D 类学生有 名； （2）将条形统计图和扇形统计图补充完整；[来源:学|科|网 Z|X|X|K] （3）若从被调查的 A 类和 D 类学生中各随机选取一位学生进行“一帮一”辅导学习，即 A 类学 生辅导 D 类学生，请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位 男同学的概率． 20．(2017·黑龙江绥化中考)已知关于 x 的一元二次方程 x2＋(2m＋1)x＋m2－4＝0. (1)当 m 为何值时，方程有两个不相等的实数根？ (2)若边长为 5 的菱形的两条对角线的长分别为方程两根的 2 倍，求 m 的值． 21．某商品的进价为每件 40 元，售价为每件 60 元时，每个月可卖出 100 件；如果每件商品的售 价每上涨 1 元，则每个月少卖 2 件．设每件商品的售价为 x 元(x 为正整数)，每个月的销售利润 为 y 元． (1)当每件商品的售价是多少元时，每个月的利润刚好是 2250 元？ (2)当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？[来源:Z_xx_k.Com] 22、如图，在 Rt△ABC 中，∠ACB=90°，∠B=30°，将△ABC 绕点 C 按顺时针方向旋转 n 度后， 得到△DEC，点 D 刚好落在 AB 边上． （1）求 n 的值； （2）若 F 是 DE 的中点，判断四边形 ACFD 的形状，并说明理由． 23、如图，AB 是⊙O 的直径，OD 垂直于弦 AC 于点 E，且交⊙O 于点 D，F 是 BA 延长线上一点， 若∠CDB=∠BFD． （1）求证：FD 是⊙O 的一条切线； （2）若 AB=10，AC=8，求 DF 的长． 24、如图 1 在平面直角坐标系中．等腰 Rt△OAB 的斜边 OA 在 x 轴上．P 为线段 OB 上﹣动点（不 与 O，B 重合）．过 P 点向 x 轴作垂线．垂足为 C．以 PC 为边在 PC 的右侧作正方形 PCDM．OP= t、 OA=3．设过 O，M 两点的抛物线为 y=ax2+bx．其顶点 N（m，n）【版权所有：21 教育】 （1）写出 t 的取值范围 ，写出 M 的坐标：（ ， ）； （2）用含 a，t 的代数式表示 b； （3）当抛物线开向下，且点 M 恰好运动到 AB 边上时（如图 2） ①求 t 的值； ②若 N 在△OAB 的内部及边上，试求 a 及 m 的取值范围． 25、．如图，在平面直角坐标系中，以点 C（1，1）为圆心，2 为半径作圆，交 x 轴于 A，B 两点， 点 P 在优弧 上．2 （1）求出 A，B 两点的坐标； （2）试确定经过 A、B 且以点 P 为顶点的抛物线解析式； （3）在该抛物线上是否存在一点 D，使线段 OP 与 CD 互相平分？若存在，求出点 D 的坐标；若 不存在，请说明理由. 21 教育名师原创作品 2017--2018 学年上学期九年级数学期末质量检测参考答案[来 源:Z.xx.k.Com] 一、选择题 1、A、 2、.B 3、D 4、C 5、D 6、C．7、B 8、D 9、B10、D 二、填空题 11、 且 a≠012、 13、0.55 ．14、 15π cm． 15. 16、﹣2+2 ＜k≤ 或 ≤k≤﹣4 +6 或 k≥15 ． 17.解：方程化为 x2－4x＝0，所以 x（x-4）=0，所以 x=0，x-4=0 所以 x1＝0，x2＝4. 18、解：（1）作图如下： （2） 线段 BC 所扫过的图形如图所示． 根据网格图知： ，所以 线段 BC 所扫过的图形的面积 = （ ） 19、解：（1）本次调查的学生数=（6+4）÷50%=20（名），[来源:学§科§网] 则 A 类女生有：20×15%﹣1=2（名），D 类学生有 20﹣（3+10+5）=2（名），[来源:学§科§网] 故答案为：20、2、2； （2）C 类百分比为 ×100%=25%，D 类别百分比为 ×100%=10%， 补全图形如下： （3）由题意画树形图如下： 从树形图看出，所有可能出现的结果共有 6 种，且每种结果出 现的可能性相等，所选一位女同 学辅导一位男同学的结果共有 2 种．所以 P（一位女同学辅导一位男同学）= = ． 20.解：(1)∵方程 x2＋(2m＋1)x＋m2－4＝0 有两个不相等的实数根，∴Δ＝(2m＋1)2－4(m2－4) ＝4m＋17＞0，解得 m＞－17 4 .∴当 m＞－17 4 时，方程有两个不相等的实数根． (2)设方程的两根 分 别为 a、b.根据题意，得 a＋b＝－2m－1，ab＝m2－4.∵2a、2b 为边长为 5 的菱形的两条对角 线的长，∴a2＋b2＝(a＋b)2－2ab＝(－2m－1)2－2(m2－4)＝2m2＋4m＋9＝52＝25，解得 m＝－4 或 m＝2.∵a＞0，b＞0，∴a＋b＝－2m－1＞0，∴m＝－4.若边长为 5 的菱形的两条对角线的长分别 为方程两根的 2 倍，则 m 的值为－4. 21 解：(1)由题意，得[100－2(x－60)](x－40)＝2250，解得 x1＝65，x2＝85.故每件商品的售 价是 65 元或 85 元时，每个月的利润刚好是 2250 元． (2)由题意，得 y＝[100－2(x－60)](x－40)＝－2x2＋300x－8800＝－2(x－75)2＋2450.当 x＝ 75 时，y 有最大值为 2450 元．故当每件商品的售价定为 75 元时，每个月可获得最大利润．最大 的月利润是 2450 元． 22、解：（1）∵在 Rt△ABC 中，∠ACB=90°，∠B=30°，将△ABC 绕点 C 按顺时针方向旋转 n 度后，得到△DEC， ∴AC=DC，∠A=60°， ∴△ADC 是等边三角形， ∴∠ACD=60°， ∴n 的值是 60； （2）四边形 ACFD 是菱形； 理由：∵∠DCE=∠ACB=90°，F 是 DE 的中点， ∴FC=DF=FE， ∵∠CDF=∠A=60°， ∴△DFC 是等边三角形， ∴DF=DC=FC， ∵△ADC 是等边三角形， ∴AD=AC=DC， ∴AD=AC=FC=DF， ∴四边形 ACFD 是菱形． 22、（1）证明：∵∠CDB=∠CAB，∠CDB=∠BFD， ∴∠CAB=∠BFD， ∴FD∥AC（同位角相等，两直线平行）， ∵∠AEO=90°， ∴∠FDO=90°， ∴FD 是⊙O 的一条切线； （2）解：∵AB=10，AC=8，DO⊥AC， ∴AE=EC=4，AO=5， ∴EO=3， ∵AE∥FD， ∴△AEO∽△FDO， ∴ = ， ∴ = ， 解得：FD= ．】 24、解：（1）如 图 1，∵△OAB 为等腰直角三角形，OA=3，∴OB=AB= = ， ∵P 为线段 OB 上﹣动点（不与 O，B 重合），∴0＜ t＜ ，∴0＜t＜ ， ∵四边形 PCDM 为正方形，∴∠PCO=90°，∵∠POC=45°，∴△POC 为等腰直角三角形， ∵OP= t，∴PC =OC=t，∴OD =t+t=2t，∴M（2t，t）； （2）把 M（2t，t）代入到 y=ax2+bx 中得：t=4at2+2tb，1=4at+2b， b= ； （3）①如图 2，∵OB= ，OP= t，∴PB= ﹣ t， ∵PM∥OA，∴ ，∴ = ，∴t=1； ②由（2）得：b= = ﹣2a，即 4a=1﹣2b， 顶点 N（﹣ ，﹣ ）（a＜0，b＞0）， i）当 0≤﹣ ≤ 时，即 a≤﹣ 时，﹣ ≥﹣ ，解得 a≥﹣ ， ∴﹣ ≤a≤﹣ ， ii）当 ＜﹣ ≤3 时，即﹣ ＜a≤﹣ ，3﹣（﹣ ）≥﹣ ，b2﹣4b+3 ≤0， 1≤b≤3，1≤ ﹣2a≤3，﹣ ≤a≤﹣ ，则﹣ ＜a≤﹣ ， 综上所述：a 的取值为：﹣ ≤a≤﹣ ，m=﹣ =1﹣ ， 得：4am=4a﹣1，a=﹣ = ，﹣ ≤ ≤﹣ ，∴ ≤m≤2． 25、解：（1）如图，作 CH⊥AB 于点 H，连接 OA，OB， ∵CH=1，半径 CB=2 ∴HB= ， 故 A（1﹣ ，0），B（1+ ，0）． （2）由圆与抛物线的对称性可知抛物线的顶点 P 的坐标为（1，3）， 设抛物线解析式 y=a（x﹣1）2+3， 把点 B（1+ ，0）代入上式，解得 a=﹣1； ∴y=﹣x2+2x+2． （3）假设存在点 D 使线段 OP 与 CD 互相平分，则四边形 OCPD 是平行四边形 ∴PC∥OD 且 PC=OD． ∵PC∥y 轴，X∴点 D 在 y 轴上．又∵PC=2，∴OD=2，即 D（0，2）． 又 D（0，2）满足 y=﹣x2+2x+2，∴点 D 在抛物线上 ∴存在 D（0，2）使线段 OP 与 CD 互相平分．