2018年江苏省无锡市中考数学试卷 28页

‎2018年江苏省无锡市中考数学试卷 ‎　‎ 一、选择题（本大题共10小题，每小题3分，共30分。在每小题所给出的四个选项中，只有一项是正确的，请用2B铅笔把答题卡上相应的选项标号涂黑)‎ ‎1．（3分）下列等式正确的是（　　）‎ A．（）2=3 B．=﹣3 C．=3 D．（﹣）2=﹣3‎ ‎2．（3分）函数y=中自变量x的取值范围是（　　）‎ A．x≠﹣4 B．x≠4 C．x≤﹣4 D．x≤4‎ ‎3．（3分）下列运算正确的是（　　）‎ A．a2+a3=a5 B．（a2）3=a5 C．a4﹣a3=a D．a4÷a3=a ‎4．（3分）下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（　　）‎ A． B． C． D．‎ ‎5．（3分）下列图形中的五边形ABCDE都是正五边形，则这些图形中的轴对称图形有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎6．（3分）已知点P（a，m），Q（b，n）都在反比例函数y=的图象上，且a＜0＜b，则下列结论一定正确的是（　　）‎ A．m+n＜0 B．m+n＞0 C．m＜n D．m＞n ‎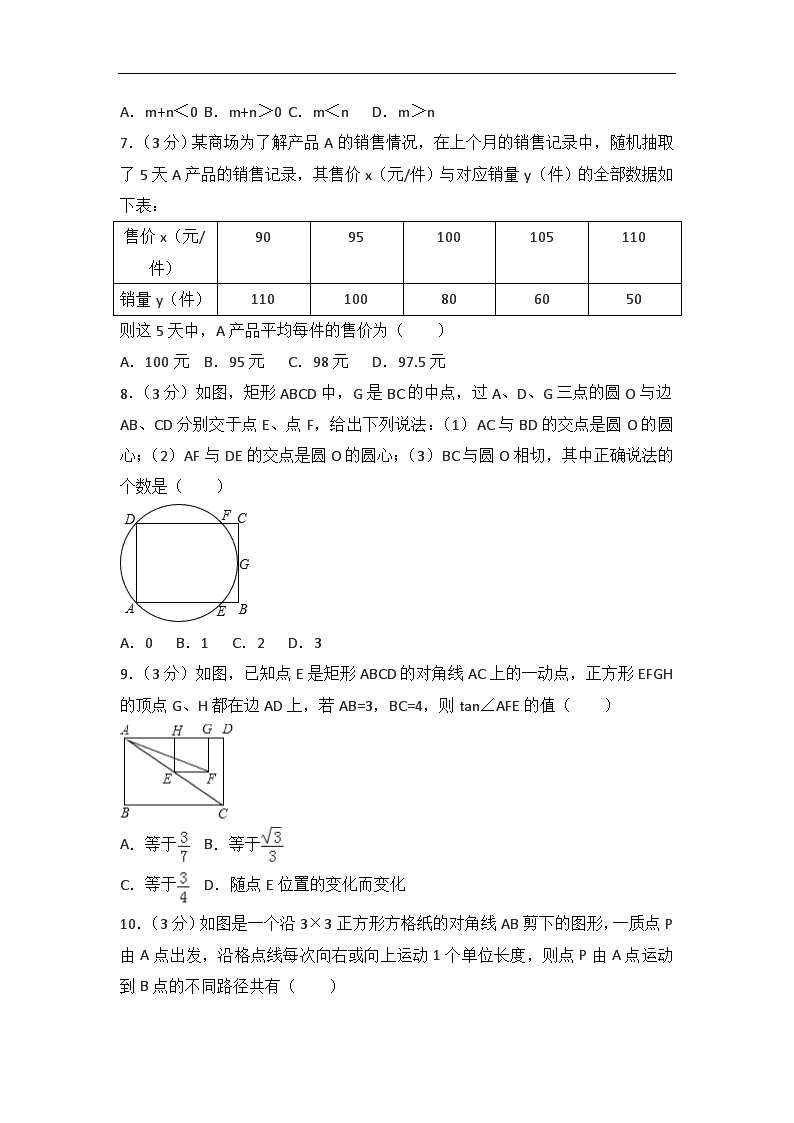7．（3分）某商场为了解产品A的销售情况，在上个月的销售记录中，随机抽取了5天A产品的销售记录，其售价x（元/件）与对应销量y（件）的全部数据如下表：‎ 售价x（元/件）‎ ‎90‎ ‎95‎ ‎100‎ ‎105‎ ‎110‎ 销量y（件）‎ ‎110‎ ‎100‎ ‎80‎ ‎60‎ ‎50‎ 则这5天中，A产品平均每件的售价为（　　）‎ A．100元 B．95元 C．98元 D．97.5元 ‎8．（3分）如图，矩形ABCD中，G是BC的中点，过A、D、G三点的圆O与边AB、CD分别交于点E、点F，给出下列说法：（1）AC与BD的交点是圆O的圆心；（2）AF与DE的交点是圆O的圆心；（3）BC与圆O相切，其中正确说法的个数是（　　）‎ A．0 B．1 C．2 D．3‎ ‎9．（3分）如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（　　）‎ A．等于 B．等于 C．等于 D．随点E位置的变化而变化 ‎10．（3分）如图是一个沿3×3正方形方格纸的对角线AB剪下的图形，一质点P由A点出发，沿格点线每次向右或向上运动1个单位长度，则点P由A点运动到B点的不同路径共有（　　）‎ A．4条 B．5条 C．6条 D．7条 ‎　‎ 二、填空题（本大题共8小题，每小题2分，共16分。不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）‎ ‎11．（2分）﹣2的相反数的值等于　 　．‎ ‎12．（2分）今年“五一”节日期间，我市四个旅游景区共接待游客约303000多人次，这个数据用科学记数法可记为　 　．‎ ‎13．（2分）方程=的解是　 　．‎ ‎14．（2分）方程组的解是　 　．‎ ‎15．（2分）命题“四边相等的四边形是菱形”的逆命题是　 　．‎ ‎16．（2分）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA=AB，则∠ABC=　 　．‎ ‎17．（2分）已知△ABC中，AB=10，AC=2，∠B=30°，则△ABC的面积等于　 　．‎ ‎18．（2分）如图，已知∠XOY=60°，点A在边OX上，OA=2．过点A作AC⊥OY于点C，以AC为一边在∠XOY内作等边三角形ABC，点P是△ABC围成的区域（包括各边）内的一点，过点P作PD∥OY交OX于点D，作PE∥OX交OY于点E．设OD=a，OE=b，则a+2b的取值范围是　 　．‎ ‎　‎ 三、解答题（本大题共10小题，共84分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎19．（8分）计算：‎ ‎（1）（﹣2）2×|﹣3|﹣（）0‎ ‎（2）（x+1）2﹣（x2﹣x）‎ ‎20．（8分）（1）分解因式：3x3﹣27x ‎（2）解不等式组：‎ ‎21．（8分）如图，平行四边形ABCD中，E、F分别是边BC、AD的中点，求证：∠ABF=∠CDE．‎ ‎22．（6分）某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．‎ 请根据以上信息，解答下列问题：‎ ‎（1）该汽车交易市场去年共交易二手轿车　 　辆．‎ ‎（2）把这幅条形统计图补充完整．（画图后请标注相应的数据）‎ ‎（3）在扇形统计图中，D类二手轿车交易辆数所对应扇形的圆心角为　 　度．‎ ‎23．（8分）某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）‎ ‎24．（8分）如图，四边形ABCD内接于⊙O，AB=17，CD=10，∠A=90°，cosB=，求AD的长．‎ ‎25．（8分）一水果店是A酒店某种水果的唯一供货商，水果店根据该酒店以往每月的需求情况，本月初专门为他们准备了2600kg的这种水果．已知水果店每售出1kg该水果可获利润10元，未售出的部分每1kg将亏损6元，以x（单位：kg，2000≤x≤3000）表示A酒店本月对这种水果的需求量，y（元）表示水果店销售这批水果所获得的利润．‎ ‎（1）求y关于x的函数表达式；‎ ‎（2）问：当A酒店本月对这种水果的需求量如何时，该水果店销售这批水果所获的利润不少于22000元？‎ ‎26．（10分）如图，平面直角坐标系中，已知点B的坐标为（6，4）．‎ ‎（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）‎ ‎（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．‎ ‎27．（10分）如图，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ（0°＜θ＜90°）得到矩形A1BC1D1，点A1在边CD上．‎ ‎（1）若m=2，n=1，求在旋转过程中，点D到点D1所经过路径的长度；‎ ‎（2）将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B与CD交于点E，若=﹣1，求的值．‎ ‎28．（10分）已知：如图，一次函数y=kx﹣1的图象经过点A（3，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．‎ ‎（1）求这个一次函数的表达式；‎ ‎（2）已知一开口向下、以直线CD为对称轴的抛物线经过点A，它的顶点为P，若过点P且垂直于AP的直线与x轴的交点为Q（﹣，0），求这条抛物线的函数表达式．‎ ‎　‎ ‎2018年江苏省无锡市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共10小题，每小题3分，共30分。在每小题所给出的四个选项中，只有一项是正确的，请用2B铅笔把答题卡上相应的选项标号涂黑)‎ ‎1．（3分）下列等式正确的是（　　）‎ A．（）2=3 B．=﹣3 C．=3 D．（﹣）2=﹣3‎ ‎【分析】根据二次根式的性质把各个二次根式化简，判断即可．‎ ‎【解答】解：（）2=3，A正确；‎ ‎=3，B错误；‎ ‎==3，C错误；‎ ‎（﹣）2=3，D错误；‎ 故选：A．‎ ‎　‎ ‎2．（3分）函数y=中自变量x的取值范围是（　　）‎ A．x≠﹣4 B．x≠4 C．x≤﹣4 D．x≤4‎ ‎【分析】根据分母不等于0列式计算即可得解．‎ ‎【解答】解：由题意得，4﹣x≠0，‎ 解得x≠4．‎ 故选：B．‎ ‎　‎ ‎3．（3分）下列运算正确的是（　　）‎ A．a2+a3=a5 B．（a2）3=a5 C．a4﹣a3=a D．a4÷a3=a ‎【分析】‎ 根据合并同类项法则，把同类项的系数相加，所得结果作为系数，字母和字母的指数不变；幂的乘方，底数不变指数相乘；同底数幂相除，底数不变指数相减，对各选项分析判断后利用排除法求解．‎ ‎【解答】解：A、a2、a3不是同类项不能合并，故A错误；‎ B、（a2）3=a6）x5•x5=x10，故B错误；‎ C、a4、a3不是同类项不能合并，故C错误；‎ D、a4÷a3=a，故D正确．‎ 故选：D．‎ ‎　‎ ‎4．（3分）下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（　　）‎ A． B． C． D．‎ ‎【分析】利用正方体及其表面展开图的特点解题．能组成正方体的“一，四，一”“三，三”“二，二，二”“一，三，二”的基本形态要记牢．‎ ‎【解答】解：能折叠成正方体的是 故选：C．‎ ‎　‎ ‎5．（3分）下列图形中的五边形ABCDE都是正五边形，则这些图形中的轴对称图形有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【分析】直接利用轴对称图形的性质画出对称轴得出答案．‎ ‎【解答】解：如图所示：直线l即为各图形的对称轴．‎ ‎，‎ 故选：D．‎ ‎　‎ ‎6．（3分）已知点P（a，m），Q（b，n）都在反比例函数y=的图象上，且a＜0＜b，则下列结论一定正确的是（　　）‎ A．m+n＜0 B．m+n＞0 C．m＜n D．m＞n ‎【分析】根据反比例函数的性质，可得答案．‎ ‎【解答】解：y=的k=﹣2＜0，图象位于二四象限，‎ ‎∵a＜0，‎ ‎∴P（a，m）在第二象限，‎ ‎∴m＞0；‎ ‎∵b＞0，‎ ‎∴Q（b，n）在第四象限，‎ ‎∴n＜0．‎ ‎∴n＜0＜m，‎ 即m＞n，‎ 故D正确；‎ 故选：D．‎ ‎　‎ ‎7．（3分）某商场为了解产品A的销售情况，在上个月的销售记录中，随机抽取了5天A产品的销售记录，其售价x（元/件）与对应销量y（件）的全部数据如下表：‎ ‎90‎ ‎95‎ ‎100‎ ‎105‎ ‎110‎ 售价x（元/件）‎ 销量y（件）‎ ‎110‎ ‎100‎ ‎80‎ ‎60‎ ‎50‎ 则这5天中，A产品平均每件的售价为（　　）‎ A．100元 B．95元 C．98元 D．97.5元 ‎【分析】根据加权平均数列式计算可得．‎ ‎【解答】解：由表可知，这5天中，A产品平均每件的售价为=98（元/件），‎ 故选：C．‎ ‎　‎ ‎8．（3分）如图，矩形ABCD中，G是BC的中点，过A、D、G三点的圆O与边AB、CD分别交于点E、点F，给出下列说法：（1）AC与BD的交点是圆O的圆心；（2）AF与DE的交点是圆O的圆心；（3）BC与圆O相切，其中正确说法的个数是（　　）‎ A．0 B．1 C．2 D．3‎ ‎【分析】连接DG、AG，作GH⊥AD于H，连接OD，如图，先确定AG=DG，则GH垂直平分AD，则可判断点O在HG上，再根据HG⊥BC可判定BC与圆O相切；接着利用OG=OG可判断圆心O不是AC与BD的交点；然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心．‎ ‎【解答】解：连接DG、AG，作GH⊥AD于H，连接OD，如图，‎ ‎∵G是BC的中点，‎ ‎∴AG=DG，‎ ‎∴GH垂直平分AD，‎ ‎∴点O在HG上，‎ ‎∵AD∥BC，‎ ‎∴HG⊥BC，‎ ‎∴BC与圆O相切；‎ ‎∵OG=OG，‎ ‎∴点O不是HG的中点，‎ ‎∴圆心O不是AC与BD的交点；‎ 而四边形AEFD为⊙O的内接矩形，‎ ‎∴AF与DE的交点是圆O的圆心；‎ ‎∴（1）错误，（2）（3）正确．‎ 故选：C．‎ ‎　‎ ‎9．（3分）如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（　　）‎ A．等于 B．等于 C．等于 D．随点E位置的变化而变化 ‎【分析】根据题意推知EF∥AD，由该平行线的性质推知△AEH∽△ACD，结合该相似三角形的对应边成比例和锐角三角函数的定义解答．‎ ‎【解答】解：∵EF∥AD，‎ ‎∴∠AFE=∠FAG，‎ ‎∴△AEH∽△ACD，‎ ‎∴==．‎ 设EH=3x，AH=4x，‎ ‎∴HG=GF=3x，‎ ‎∴tan∠AFE=tan∠FAG===．‎ 故选：A．‎ ‎　‎ ‎10．（3分）如图是一个沿3×3正方形方格纸的对角线AB剪下的图形，一质点P由A点出发，沿格点线每次向右或向上运动1个单位长度，则点P由A点运动到B点的不同路径共有（　　）‎ A．4条 B．5条 C．6条 D．7条 ‎【分析】将各格点分别记为1、2、3、4、5、6、7，利用树状图可得所有路径．‎ ‎【解答】解：如图，将各格点分别记为1、2、3、4、5、6、7，‎ 画树状图如下：‎ 由树状图可知点P由A点运动到B点的不同路径共有5种，‎ 故选：B．‎ ‎　‎ 二、填空题（本大题共8小题，每小题2分，共16分。不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）‎ ‎11．（2分）﹣2的相反数的值等于　2　．‎ ‎【分析】根据相反数的定义作答．‎ ‎【解答】解：﹣2的相反数的值等于 2．‎ 故答案是：2．‎ ‎　‎ ‎12．（2分）今年“五一”节日期间，我市四个旅游景区共接待游客约303000多人次，这个数据用科学记数法可记为　3.03×105　．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于303000有6位整数，所以可以确定n=6﹣1=5．‎ ‎【解答】解：303000=3.03×105，‎ 故答案为：3.03×105．‎ ‎　‎ ‎13．（2分）方程=的解是　x=﹣　．‎ ‎【分析】方程两边都乘以x（x+1）化分式方程为整式方程，解整式方程得出x的值，再检验即可得出方程的解．‎ ‎【解答】解：方程两边都乘以x（x+1），得：（x﹣3）（x+1）=x2，‎ 解得：x=﹣，‎ 检验：x=﹣时，x（x+1）=≠0，‎ 所以分式方程的解为x=﹣，‎ 故答案为：x=﹣．‎ ‎　‎ ‎14．（2分）方程组的解是　　．‎ ‎【分析】利用加减消元法求解可得．‎ ‎【解答】解：，‎ ‎②﹣①，得：3y=3，‎ 解得：y=1，‎ 将y=1代入①，得：x﹣1=2，‎ 解得：x=3，‎ 所以方程组的解为，‎ 故答案为：．‎ ‎　‎ ‎15．（2分）命题“四边相等的四边形是菱形”的逆命题是　菱形的四条边相等　．‎ ‎【分析】把一个命题的条件和结论互换就得到它的逆命题．‎ ‎【解答】解：命题“四边相等的四边形是菱形”的逆命题是菱形的四条边相等，‎ 故答案为：菱形的四条边相等．‎ ‎　‎ ‎16．（2分）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA=AB，则∠ABC=　15°　．‎ ‎【分析】根据等边三角形的判定和性质，再利用圆周角定理解答即可．‎ ‎【解答】解：∵OA=OB，OA=AB，‎ ‎∴OA=OB=AB，‎ 即△OAB是等边三角形，‎ ‎∴∠AOB=60°，‎ ‎∵OC⊥OB，‎ ‎∴∠COB=90°，‎ ‎∴∠COA=90°﹣60°=30°，‎ ‎∴∠ABC=15°，‎ 故答案为：15°‎ ‎　‎ ‎17．（2分）已知△ABC中，AB=10，AC=2，∠B=30°，则△ABC的面积等于　15或10　．‎ ‎【分析】作AD⊥BC交BC（或BC延长线）于点D，分AB、AC位于AD异侧和同侧两种情况，先在Rt△ABD中求得AD、BD的值，再在Rt△ACD中利用勾股定理求得CD的长，继而就两种情况分别求出BC的长，根据三角形的面积公式求解可得．‎ ‎【解答】解：作AD⊥BC交BC（或BC延长线）于点D，‎ ‎①如图1，当AB、AC位于AD异侧时，‎ 在Rt△ABD中，∵∠B=30°，AB=10，‎ ‎∴AD=ABsinB=5，BD=ABcosB=5，‎ 在Rt△ACD中，∵AC=2，‎ ‎∴CD===，‎ 则BC=BD+CD=6，‎ ‎∴S△ABC=•BC•AD=×6×5=15；‎ ‎②如图2，当AB、AC在AD的同侧时，‎ 由①知，BD=5，CD=，‎ 则BC=BD﹣CD=4，‎ ‎∴S△ABC=•BC•AD=×4×5=10．‎ 综上，△ABC的面积是15或10，‎ 故答案为15或10．‎ ‎　‎ ‎18．（2分）如图，已知∠XOY=60°，点A在边OX上，OA=2．过点A作AC⊥OY于点C，以AC为一边在∠XOY内作等边三角形ABC，点P是△ABC围成的区域（包括各边）内的一点，过点P作PD∥OY交OX于点D，作PE∥OX交OY于点E．设OD=a，OE=b，则a+2b的取值范围是　2≤a+2b≤5　．‎ ‎【分析】作辅助线，构建30度的直角三角形，先证明四边形EODP是平行四边形，得EP=OD=a，在Rt△HEP中，∠EPH=30°，可得EH的长，计算a+2b=2OH，确认OH最大和最小值的位置，可得结论．‎ ‎【解答】解：过P作PH⊥OY交于点H，‎ ‎∵PD∥OY，PE∥OX，‎ ‎∴四边形EODP是平行四边形，∠HEP=∠XOY=60°，‎ ‎∴EP=OD=a，‎ Rt△HEP中，∠EPH=30°，‎ ‎∴EH=EP=a，‎ ‎∴a+2b=2（a+b）=2（EH+EO）=2OH，‎ 当P在AC边上时，H与C重合，此时OH的最小值=OC=OA=1，即a+2b的最小值是2；‎ 当P在点B时，OH的最大值是：1+=，即（a+2b）的最大值是5，‎ ‎∴2≤a+2b≤5．‎ ‎　‎ 三、解答题（本大题共10小题，共84分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎19．（8分）计算：‎ ‎（1）（﹣2）2×|﹣3|﹣（）0‎ ‎（2）（x+1）2﹣（x2﹣x）‎ ‎【分析】（1）本题涉及零指数幂、乘方、绝对值3个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．‎ ‎（2）根据完全平方公式和去括号法则计算，再合并同类项即可求解．‎ ‎【解答】解：（1）（﹣2）2×|﹣3|﹣（）0‎ ‎=4×3﹣1‎ ‎=12﹣1‎ ‎=11；‎ ‎（2）（x+1）2﹣（x2﹣x）‎ ‎=x2+2x+1﹣x2+x ‎=3x+1．‎ ‎　‎ ‎20．（8分）（1）分解因式：3x3﹣27x ‎（2）解不等式组：‎ ‎【分析】（1）先提取公因式3x，再利用平方差公式分解可得；‎ ‎（2）分别求出各不等式的解集，再求出其公共解集．‎ ‎【解答】解：（1）原式=3x（x2﹣9）‎ ‎=3x（x+3）（x﹣3）；‎ ‎（2）解不等式①，得：x＞﹣2，‎ 解不等式②，得：x≤2，‎ 则不等式组的解集为﹣2＜x≤2．‎ ‎　‎ ‎21．（8分）如图，平行四边形ABCD中，E、F分别是边BC、AD的中点，求证：∠ABF=∠CDE．‎ ‎【分析】根据平行四边形的性质以及全等三角形的性质即可求出答案．‎ ‎【解答】解：在▱ABCD中，‎ AD=BC，∠A=∠C，‎ ‎∵E、F分别是边BC、AD的中点，‎ ‎∴AF=CE，‎ 在△ABF与△CDE中，‎ ‎∴△ABF≌△CDE（SAS）‎ ‎∴∠ABF=∠CDE ‎　‎ ‎22．（6分）某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．‎ 请根据以上信息，解答下列问题：‎ ‎（1）该汽车交易市场去年共交易二手轿车　3000　辆．‎ ‎（2）把这幅条形统计图补充完整．（画图后请标注相应的数据）‎ ‎（3）在扇形统计图中，D类二手轿车交易辆数所对应扇形的圆心角为　54　度．‎ ‎【分析】（1）根据B类别车辆的数量及其所占百分比可得总数量；‎ ‎（2）用总数量乘以C类别的百分比求得其数量，据此即可补全条形图；‎ ‎（3）用360°乘以D类车辆占总数量的比例即可得出答案．‎ ‎【解答】解：（1）该汽车交易市场去年共交易二手轿车1080÷36%=3000辆，‎ 故答案为：3000；‎ ‎（2）C类别车辆人数为3000×25%=750辆，‎ 补全条形统计图如下：‎ ‎（3）在扇形统计图中，D类二手轿车交易辆数所对应扇形的圆心角为360°×=54°，‎ 故答案为：54．‎ ‎　‎ ‎23．（8分）某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）‎ ‎【分析】列表得出所有等可能的情况数，找出抽到由男生甲、女生丙和这位班主任一起上场参赛的情况数，即可求出所求的概率．‎ ‎【解答】解：可能出现的所有结果列表如下：‎ 甲 乙 丙 ‎（甲，丙）‎ ‎（乙，丙）‎ 丁 ‎（甲，丁）‎ ‎（乙，丁）‎ 共有4种可能的结果，且每种的可能性相同，其中恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的结果有1种，‎ 所以恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率为．‎ ‎　‎ ‎24．（8分）如图，四边形ABCD内接于⊙O，AB=17，CD=10，∠A=90°，cosB=，求AD的长．‎ ‎【分析】根据圆内接四边形的对角互补得出∠C=90°，∠ABC+∠ADC=180°．作AE⊥BC于E，DF⊥AE于F，则CDFE是矩形，EF=CD=10．解Rt△AEB，得出BE=AB•cos∠ABE=，AE==，那么AF=AE﹣EF=．再证明∠ABC+∠ADF=90°，根据互余角的互余函数相等得出sin∠ADF=cos∠ABC=．解Rt△ADF，即可求出AD==6．‎ ‎【解答】解：∵四边形ABCD内接于⊙O，∠A=90°，‎ ‎∴∠C=180°﹣∠A=90°，∠ABC+∠ADC=180°．‎ 作AE⊥BC于E，DF⊥AE于F，则CDFE是矩形，EF=CD=10．‎ 在Rt△AEB中，∵∠AEB=90°，AB=17，cos∠ABC=，‎ ‎∴BE=AB•cos∠ABE=，‎ ‎∴AE==，‎ ‎∴AF=AE﹣EF=﹣10=．‎ ‎∵∠ABC+∠ADC=180°，∠CDF=90°，‎ ‎∴∠ABC+∠ADF=90°，‎ ‎∵cos∠ABC=，‎ ‎∴sin∠ADF=cos∠ABC=．‎ 在Rt△ADF中，∵∠AFD=90°，sin∠ADF=，‎ ‎∴AD===6．‎ ‎　‎ ‎25．（8分）一水果店是A酒店某种水果的唯一供货商，水果店根据该酒店以往每月的需求情况，本月初专门为他们准备了2600kg的这种水果．已知水果店每售出1kg该水果可获利润10元，未售出的部分每1kg将亏损6元，以x（单位：kg，2000≤x≤3000）表示A酒店本月对这种水果的需求量，y（元）表示水果店销售这批水果所获得的利润．‎ ‎（1）求y关于x的函数表达式；‎ ‎（2）问：当A酒店本月对这种水果的需求量如何时，该水果店销售这批水果所获的利润不少于22000元？‎ ‎【分析】（1）列函数解析式时注意在获得的利润里减去未出售的亏损部分；‎ ‎（2）由（1）y≥22000即可．‎ ‎【解答】解：（1）由题意：‎ 当2 000≤x≤2 600时，y=10x﹣6（2600﹣x）=16x﹣15600；‎ 当2 600＜x≤3 000时，y=2600×10=26000‎ ‎（2）由题意得：‎ ‎16x﹣15600≥22000‎ 解得：x≥2350‎ ‎∴当A酒店本月对这种水果的需求量小于等于3000，不少于2350kg时，该水果店销售这批水果所获的利润不少于22000元．‎ ‎　‎ ‎26．（10分）如图，平面直角坐标系中，已知点B的坐标为（6，4）．‎ ‎（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）‎ ‎（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．‎ ‎【分析】（1）①作线段OB的垂直平分线AC，满足条件，②作矩形OA′BC′，直线A′C′，满足条件；‎ ‎（2）分两种情形分别求解即可解决问题；‎ ‎【解答】（1）解：如图△ABC即为所求；‎ ‎（2）解：这样的直线不唯一．‎ ‎①作线段OB的垂直平分线AC，满足条件，此时直线的解析式为y=﹣x+．‎ ‎②作矩形OA′BC′，直线A′C′，满足条件，此时直线A′C′的解析式为y=﹣x+4．‎ ‎　‎ ‎27．（10分）如图，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ（0°＜θ＜90°）得到矩形A1BC1D1，点A1在边CD上．‎ ‎（1）若m=2，n=1，求在旋转过程中，点D到点D1所经过路径的长度；‎ ‎（2）将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B与CD交于点E，若=﹣1，求的值．‎ ‎【分析】（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．解直角三角形，求出∠ABA1，得到旋转角即可解决问题；‎ ‎（2）由△BCE∽△BA2D2，推出==，可得CE=由=﹣1推出=，推出A1C=•，推出BH=A1C==•，可得m2﹣n2=6•‎ ‎，可得1﹣=6•，由此解方程即可解决问题；‎ ‎【解答】解：（1）作A1H⊥AB于H，连接BD，BD1，则四边形ADA1H是矩形．‎ ‎∴AD=HA1=n=1，‎ 在Rt△A1HB中，∵BA1=BA=m=2，‎ ‎∴BA1=2HA1，‎ ‎∴∠ABA1=30°，‎ ‎∴旋转角为30°，‎ ‎∵BD==，‎ ‎∴D到点D1所经过路径的长度==π．‎ ‎（2）∵△BCE∽△BA2D2，‎ ‎∴==，‎ ‎∴CE=‎ ‎∵=﹣1‎ ‎∴=，‎ ‎∴AC=•，‎ ‎∴BH=AC==•，‎ ‎∴m2﹣n2=6•，‎ ‎∴m4﹣m2n2=6n4，‎ ‎1﹣=6•，‎ ‎∴=（负根已经舍弃）．‎ ‎　‎ ‎28．（10分）已知：如图，一次函数y=kx﹣1的图象经过点A（3，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．‎ ‎（1）求这个一次函数的表达式；‎ ‎（2）已知一开口向下、以直线CD为对称轴的抛物线经过点A，它的顶点为P，若过点P且垂直于AP的直线与x轴的交点为Q（﹣，0），求这条抛物线的函数表达式．‎ ‎【分析】（1）利用三角形相似和勾股定理构造方程，求AC和m ‎（2）由∠APQ=90°，构造△PQD∽△APE构造方程求点P坐标可求二次函数解析式．‎ ‎【解答】解：（1）过点A作AF⊥x轴，过点B作BF⊥CD于H，交AF于点F，过点C作CE⊥AF于点E 设AC=n，则CD=n ‎∵点B坐标为（0，﹣1）‎ ‎∴CH=n+1，AF=m+1‎ ‎∵CH∥AF，BC=2AC ‎∴‎ 即：‎ 整理得：‎ n=‎ Rt△AEC中，‎ CE2+AE2=AC2‎ ‎∴5+（m﹣n）2=n2‎ 把n=代入 ‎5+（m﹣）2=（）2‎ 解得m1=5，m2=﹣3（舍去）‎ ‎∴n=3‎ ‎∴把A（3，5）代入y=kx﹣1得 k=‎ ‎∴y=x﹣1‎ ‎（2）如图，过点A作AE⊥CD于点E 设点P坐标为（2，n），由已知n＞0‎ 由已知，PD⊥x轴 ‎∴△PQD∽△APE ‎∴‎ ‎∴‎ 解得n1=7，n2=﹣2（舍去）‎ 设抛物线解析式为y=a（x﹣h）2+k ‎∴y=a（x﹣2）2+7‎ 把A（3，5）代入y=a（x﹣2）2+7‎ 解得a=﹣‎ ‎∴抛物线解析式为：y=﹣‎ ‎　‎