第三章：图形的相似复习与小结 3页

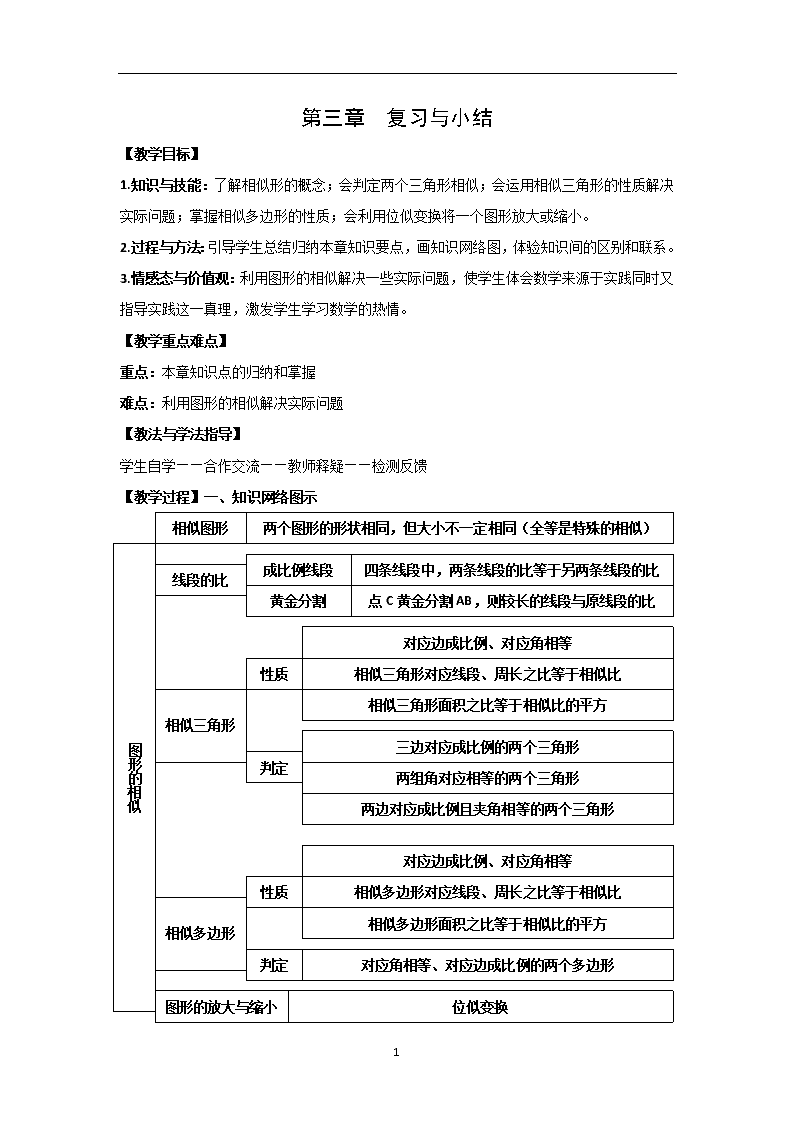
第三章　复习与小结 ‎【教学目标】‎ ‎1.知识与技能：了解相似形的概念；会判定两个三角形相似；会运用相似三角形的性质解决实际问题；掌握相似多边形的性质；会利用位似变换将一个图形放大或缩小。‎ ‎2.过程与方法：引导学生总结归纳本章知识要点，画知识网络图，体验知识间的区别和联系。‎ ‎3.情感态与价值观：利用图形的相似解决一些实际问题，使学生体会数学来源于实践同时又指导实践这一真理，激发学生学习数学的热情。‎ ‎【教学重点难点】‎ 重点：本章知识点的归纳和掌握 难点：利用图形的相似解决实际问题 ‎【教法与学法指导】‎ 学生自学——合作交流——教师释疑——检测反馈 ‎【教学过程】一、知识网络图示 两个图形的形状相同，但大小不一定相同（全等是特殊的相似）‎ 相似图形 ‎ 四条线段中，两条线段的比等于另两条线段的比 成比例线段 图形的相似 形 的 相 似 线段的比 对应边成比例、对应角相等 相似多边形对应线段、周长之比等于相似比 相似多边形面积之比等于相似比的平方 性质 相似三角形 相似多边形 对应角相等、对应边成比例的两个多边形 判定 图形的放大与缩小 两边对应成比例且夹角相等的两个三角形 两组角对应相等的两个三角形 三边对应成比例的两个三角形 相似三角形面积之比等于相似比的平方 相似三角形对应线段、周长之比等于相似比 对应边成比例、对应角相等 黄金分割 点C黄金分割AB，则较长的线段与原线段的比 性质 判定 位似变换 3‎ 二、典型例题讲析 例1.已知= = ，求 的值 例2.已知:如图2,在△ABC中,∠ADE=∠C,则下列等式成立的是( )‎ ‎ A. B. ‎ C. D.。‎ 例3.已知三个数,请你再添一个数,写出一个比例式________.‎ 例4.把△ABC的各边都扩大为原来的2倍，得到△,下面结论不正确的是( )‎ A.△ABC∽△ ‎ ‎ B.△ABC和△的各边、各角对应相等 C.△ABC和△的相似比为1:2‎ D.△ABC和△的相似比为1:3‎ 例5. 如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证: △DEH～△BCA 三、小结反思 ‎1.本章的知识网络 ‎2.相似三角形的性质与判定 ‎3.位似变换将图形放大或缩小 四、练习反馈 ‎1. 如图, D、E是AB的三等分点, DF∥EG∥BC , 图中 ‎ 三部分的面积分别为S1,S2,S 3, 则S1:S2:S3( )‎ A.1:2:3 B.1:2:4 ‎ C.1:3:5 D.2:3:4‎ ‎2.如图,四边形AEFD与EBCF是相似的梯形,AE:EB＝2:3,EF＝12 cm,求AD、BC的长.‎ ‎3.如图, 平行四边形ABCD中,点E是DC中点, 连AE并延长与BC延长线交于点F,‎ 若＝10 , 求四边形ABCE的面积.‎ ‎4.已知如图,平行四边形ABCD中,AE:EB＝1:2 .‎ ‎(1)求AE:DC的值.‎ ‎(2)△AEF与△CDF相似吗?若相似,请说明理由,‎ 3‎ 并求出相似比.‎ ‎(3)如果＝6cm2,求 ‎ （2） （3） （4）‎ 五、作业布置 P94-95 复习题三 第1、5、7、8题 六、教学反思： ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 3‎