2019年北京市大兴区中考数学一模试卷（含答案解析） 21页

2019 年北京市大兴区中考数学一模试卷 一．选择题（共 10 小题，满分 30 分，每小题 3 分） 1．下列运算正确的是（ ） A．a3+a3＝2a6 B．a6÷a﹣3＝a3 C．a3•a2＝a6 D．（﹣2a2）3＝﹣8a6 2．方程组 的解为（ ） A． B． C． D． 3．不等式组 的解集在数轴上表示为（ ） A． B． C． D． 4．如图，某电信公司提供了 A，B 两种方案的移动通讯费用 y（元）与通话时间 x（元）之 间的关 系，则下列结论中正确的有（ ） （1）若通话时间少于 120 分，则 A 方案比 B 方案便宜 20 元； （2）若通话时间超过 200 分，则 B 方案比 A 方案便宜 12 元； （3）若通讯费用为 60 元，则 B 方案比 A 方案的通话时间多； （4）若两种方 案通讯费用相差 10 元，则通话时间是 145 分或 185 分． A．1 个 B．2 个 C．3 个 D．4 个 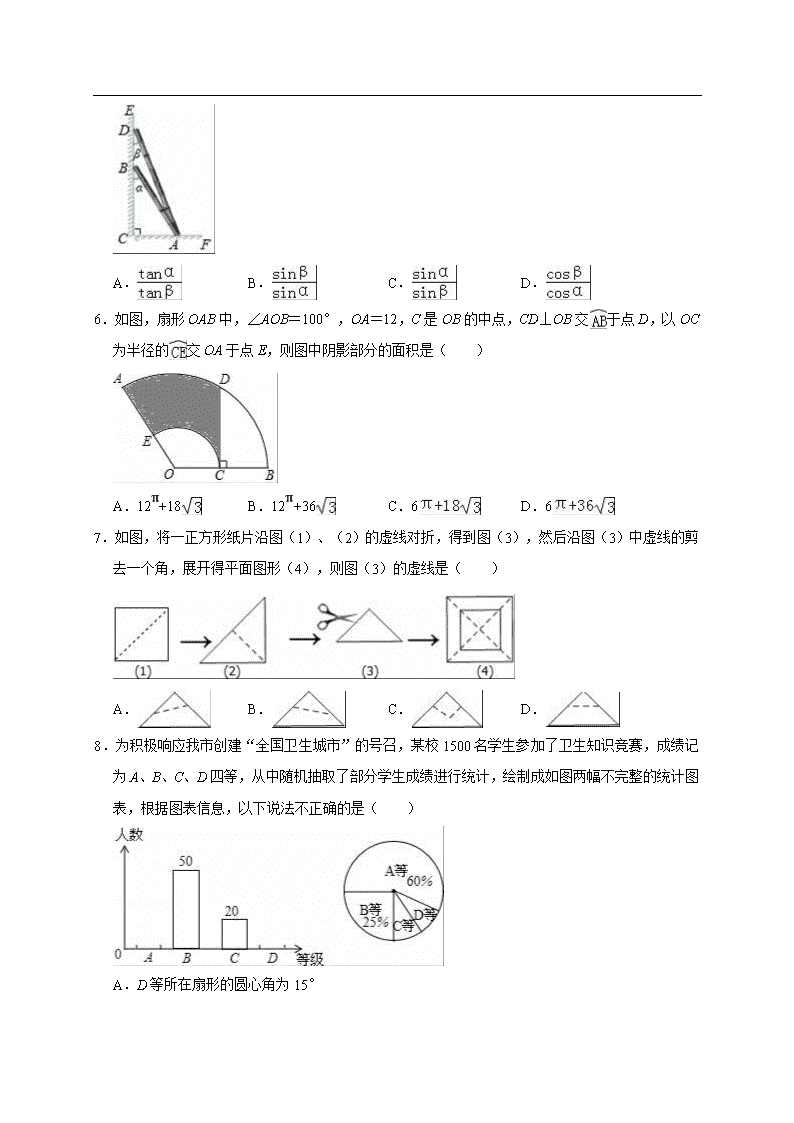5．如图，两根竹竿 AB 和 AD 斜靠在墙 CE 上，量得∠ABC＝ α ，∠ADC＝ β ，则竹竿 AB 与 AD 的长 度之比为（ ） A． B． C． D． 6．如图，扇形 OAB 中，∠AOB＝100°，OA＝12，C 是 OB 的中点，CD⊥OB 交 于点 D，以 OC 为半径的 交 OA 于点 E，则图中阴影部分的面积是（ ） A．12 π +18 B．12 π +36 C．6 D．6 7．如图，将一正方形纸片沿图（1）、（2）的虚线对折，得到图（3），然后沿图（3）中虚线的剪 去一个角，展开得平面图形（4），则图（3）的虚线是（ ） A． B． C． D． 8．为积极响应我市创建“全国卫生城市”的号召，某校 1500 名学生参加了卫生知识竞赛，成绩记 为 A、B、C、D 四等，从中随机抽取了部分学生成绩进行统计，绘制成如图两幅不完整的统计图 表，根据图表信息，以下说法不正确的是（ ） A．D 等所在扇形的圆心角为 15° B．样本容量是 200 C．样本中 C 等所占百分比是 10% D．估计全校学生成绩为 A 等大约有 900 人 9．笔筒中有 10 支型号、颜色完全相同的铅笔，将它们逐一标上 1﹣10 的号码，若从笔筒中任意抽 出一支铅笔，则抽到编号是 3 的倍数的概率是（ ） A． B． C． D． 10．如图所示，如果将矩形纸沿虚线 ① 对折后，沿虚线 ② 剪开，剪出一个直角三角形，展开后得到 一个等腰三角形．则展开后三角形的周长是（ ） A．2+ B．2+2 C．12 D．18 二．填空题（共 6 小题，满分 18 分，每小题 3 分） 11．当 x＝ 时，分式 的值为零． 12．已知 m、n 是一元二次方程 x2+4x﹣1＝0 的两实数根，则 ＝ ． 13．如图，△ABC 的两条高 AD，BE 相交于点 F，请添加一个条件，使得△ADC≌△BEC（不添加 其他字母及辅助线），你添加的条件是 ． 14．如图，将半径为 4，圆心角为 90°的扇形 BAC 绕 A 点逆时针旋转 60°，点 B、C 的对应点分别 为点 D、E 且点 D 刚好在 上，则阴影部分的面积为 ． 15．从﹣2，﹣1，0，1，2 这 5 个数中，随机抽取一个数记为 a，则使关于 x 的不等式组 有解，且使关于 x 的一元一次方程 +1＝ 的解为负数的概率为 ． 16．如图，在直角坐标系中，矩形 OABC 的顶点 C 在 x 轴的负半轴上，点 A 在 y 轴正半轴上，矩形 OABC 的面积为 ．把矩形 OABC 沿 DE 翻折，使点 B 与点 O 重合，点 C 落在第三象限的 G 点处，作 EH⊥x 轴于 H，过 E 点的反比例函数 y＝ 图象恰好过 DE 的中点 F．则 k＝ ， 线段 EH 的长为： ． 三．解答题（共 7 小题） 17．先化简，再求值：1﹣ ，其中 x、y 满足|x﹣2|+（2x﹣y﹣3）2＝0． 18．△ABC 在平面直角坐标系中的位置如图所示． （1）作出△ABC 关于 y 轴对称的△A1B1C1，并写出△A1B1C1 各顶点的坐标； （2）将△ABC 向右平移 6 个单位，作出平移后的△A2B2C2，并写出△A2B2C2 各顶点的坐标； （3）观察△A1B1C1 和△A2B2C2，它们是否关于某直线对称？若是，请在图上画出这条对称轴． 19．某服装店用 4400 元购进 A，B 两种新式服装，按标价售出后可获得毛利润 2800 元（毛利润＝ 售价﹣进价），这两种服装的进价，标价如表所示． 类型价格 A 型 B 型 进价（元/件） 60 100 标价（元/件） 100 160 （1）请利用二元一次方程组求这两种服装各购进的件数； （2）如果 A 种服装按标价的 9 折出售，B 种服装按标价的 8 折出售，那么这批服装全部售完后， 服装店比按标价出售少收入多少元？ 20．（1）问题发现 如图 1，△A CB 和△DCE 均为等边三角形，点 A，D，E 在同一直线上，连接 BE． 填空： ① ∠AEB 的度数为 ； ② 线段 AD，BE 之间的数量关系为 ． （2）拓展探究 如图 2，△ACB 和△DCE 均为等腰直角三角形，∠ACB＝∠DCE＝90°，点 A，D，E 在同一直 线上，CM 为△DCE 中 DE 边上的高，连接 BE，请判断∠AEB 的度数及线段 CM，AE，BE 之间 的数量关系，并说明理由． 21．如图，在平面直角坐标系中，直线 y＝kx﹣4k+4 与抛物线 y＝ x2﹣x 交于 A、B 两点． （1）直线总经过定点，请直接写出该定点的坐标； （2）点 P 在抛物线上，当 k＝﹣ 时，解决下列问题：[来源:学*科*网] ① 在直线 AB 下方的抛物线上求点 P，使得△PAB 的面积等于 20； ② 连接 OA，OB，OP，作 PC⊥x 轴于点 C，若△POC 和△ABO 相似，请直接写出点 P 的坐标． 22．一次安全知识测验中，学生得分均为整数，满分 10 分，成绩达到 9 分为优秀，这次测验中甲、 乙两组学生人数相同，成绩如下两个统计图： （1）在乙组学生成绩统计图中，8 分所在的扇形的圆心角为 度； （2）请补充完整下面的成绩统计分析表： 平均分[来源:学&科&网 Z&X&X&K] 方差 众数 中位数 优秀率 甲组 7 1.8 7 7 20% 乙组 [来源:学科网 ZXXK] 10% （3）甲组学生说他们的优秀率高于乙组，所以他们的成绩好于乙组，但乙组学生不同意甲组学 生的说法，认为他们组的成绩要好于甲组，请你给出两条支持乙组学生观点的理由． 23．如图，在平面直角坐标系 xOy 中，直线 y＝﹣ x+b 与 x 轴相交于点 A，与 y 轴相交于点 B，抛 物线 y＝ax2﹣4ax+4 经过点 A 和点 B，并与 x 轴相交于另一点 C，对称轴与 x 轴相交于点 D． （1）求抛物线的表达式； （2）求证：△BOD∽△AOB； （3）如果点 P 在线段 AB 上，且∠BCP＝∠DBO，求点 P 的坐标． 2019 年北京市大兴区中考数学一模试卷 参考答案与试题解析 一．选择题（共 10 小题，满分 30 分，每小题 3 分） 1．【分析】根据合并同类项法则、同底数幂相除、同底数幂相乘及幂的乘方 【解答】解：A、a3+a3＝2a3，此选项错误； B、a6÷a﹣3＝a9，此选项错误； C、a3•a2＝a5，此选项错误； D、（﹣2a2）3＝﹣8a6，此选项正确； 故选：D． 【点评】本题主要考查幂的运算，解题的关键是掌握合并同类项法则、同底数幂相除、同底数幂 相乘及幂的乘方的运算法则． 2．【分析】方程组利用加减消元法求出解即可； 【解答】解： ， ① ×3﹣ ② 得：5y＝﹣5，即 y＝﹣1， 将 y＝﹣1 代入 ① 得：x＝2， 则方程组的解为 ； 故选：D． 【点评】此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键． 3．【分析】先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集 表示在数轴上即可 【解答】解：由 x﹣1≥0，得 x≥1， 由 4﹣2x＞0，得 x＜2， 不等式组的解集是 1≤x＜2， 故选：D． 【点评】考查了解一元一次不等式组，在数轴上表示不等式的解集，把每个不等式的解集在数轴 上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一 段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几 个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要 用空心圆点表示． 4．【分析】根据图象知道：在通话 170 分钟收费一样，在通话 120 时 A 收费 30 元，B 收费 50 元， 其中 A 超过 120 分钟后每分钟加收 0.4 元，B 超过 200 分钟加收每分钟 0.4 元，由此即可确定有 几个正确． 【解答】解：依题意得 A：（1）当 0≤x≤120，yA＝30， （2）当 x＞120，yA＝30+（x﹣120）×[（50﹣30）÷（170﹣120）]＝0.4x﹣18； B：（1）当 0≤x＜200，yB＝50， 当 x＞200，yB＝50+[（70﹣50）÷（250﹣200）]（x﹣200）＝0.4x﹣30， 所以当 x≤120 时，A 方案比 B 方案便宜 20 元，故（1）正确； 当 x≥200 时，B 方案比 A 方案便宜 12 元，故（2）正确； 当 y＝60 时，A：60＝0.4x﹣18，∴x＝195， B：60＝0.4x﹣30，∴x＝225，故（3）正确；[来源:Zxxk.Com] 当 B 方案为 50 元，A 方案是 40 元或者 60 元时，两种方案通讯费用相差 10 元， 将 yA＝40 或 60 代入，得 x＝145 分或 195 分，故（4）错误； 故选：C． 【点评】此题主要考查了函数图象和性质，解题的关键是从图象中找出隐含的信息解决问题． 5．【分析】在两个直角三角形中，分别求出 AB、AD 即可解决问题． 【解答】解：在 Rt△ABC 中，AB＝ ， 在 Rt△ACD 中，AD＝ ， ∴AB：AD＝ ： ＝ ， 故选：B． 【点评】本题考查解直角三角形的应用、锐角三角函数等知识，解题的关键是学会利用参数解决 问题，属于中考常考题型． 6．【分析】连接 OD、BD，根据点 C 为 OB 的中点可得∠CDO＝30°，继而可得△BDO 为等边三 角形，求出扇形 BOD 的面积，最后用扇形 AOB 的面积减去扇形 COE 的面积，再减去 S 空白 BDC 即可求出阴影部分的面积． 【解答】解：如图，连接 OD，BD， ∵点 C 为 OB 的中点， ∴OC＝ OB＝ OD， ∵CD⊥OB， ∴∠CDO＝30°，∠DOC＝60°， ∴△BDO 为等边三角形，OD＝OB＝12，OC＝CB＝6， ∴CD＝，6 ， ∴S 扇形 BOD＝ ＝24 π ， ∴S 阴影＝S 扇形 AOB﹣S 扇形 COE﹣（S 扇形 BOD﹣S△COD ＝ ﹣ ﹣（24 π ﹣ ×6×6 ） ＝18 +6 π ． 或 S 阴＝S 扇形 OAD+S△ODC﹣S 扇形 OEC＝18 +6 π ． 故选：C． 【点评】本题考查了扇形的面积计算，解答本题的关键是掌握扇形的面积公式：S＝ ． 7．【分析】对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现． 【解答】解：由于得到的图形的中间是正方形，那么它的四分之一为等腰直角三角形． 故选：D． 【点评】本题主要考查剪纸问题，关键是培养学生的空间想象能力和动手操作能力． 8．【分析】结合统计图的数据，正确的分析求解即可得出答案． 【解答】解：样本容量是 50÷25%＝200，故 B 正确， 样本中 C 等所占百分比是 ＝10%，故 C 正确， 估计全校学生成绩为 A 等大约有 1500×60%＝900 人，故 D 正确， D 等所在扇形的圆心角为 360°×（1﹣60%﹣25%﹣10%）＝18°，故 A 不正确． 故选：A． 【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得 到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接 反映部分占总体的百分比大小． 9．【分析】由标有 1﹣10 的号码的 10 支铅笔中，标号为 3 的倍数的有 3、6、9 这 3 种情况，利用 概率公式计算可得． 【解答】解：∵在标有 1﹣10 的号码的 10 支铅笔中，标号为 3 的倍数的有 3、6、9 这 3 种情况， ∴抽到编号是 3 的倍数的概率是 ， 故选：C． 【点评】本题主要考查概率公式的应用，解题的关键是掌握随机事件 A 的概率 P（A）＝事件 A 可能出现的结果数÷所有可能出现的结果数． 10．【分析】折叠后长方形的长为原来长的一半，减去 4 后即为得到等腰三角形底边长的一半；利 用勾股定理即可求得等腰三角形的斜边长，周长＝底边长+2 腰长． 【解答】解：展开后 等腰三角形的底边长为 2×（10÷2﹣4）＝2； 腰长＝ ＝ ， 所以展开后三角形的周长是 2+2 ，故选 B． 【点评】解决本题的难点是利用折叠的性质得到等腰三角形的底边长． 二．填空题（共 6 小题，满分 18 分，每小题 3 分） 11．【分析】要使分式的值为 0，必须分式分子的值为 0 并且分母的值不为 0． 【解答】解：由分子 x2﹣4＝0 ⇒ x＝±2； 而 x＝2 时，分母 x+2＝2+2＝4≠0， x＝﹣2 时分母 x+2＝0，分式没有意义． 所以 x＝2． 故答案为：2． 【点评】要注意分母的值一定不能为 0，分母的值是 0 时分式没有意义． 12．【分析】先由根与系数的关系求出 m•n 及 m+n 的值，再把 化为 的形式代入进行计算 即可． 【解答】解：∵m、n 是一元二次方程 x2+4x﹣1＝0 的两实数根， ∴m+n＝﹣4，m•n＝﹣1， ∴ ＝ ＝ ＝4． 故答案为 4． 【点评】本题考查的是根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常 使用的解题方法．一元二次方程 ax2+bx+c＝0（a≠0）的根与系数的关系为：x1+x2＝﹣ ，x1•x2 ＝ ． 13．【分析】添加 AC＝BC，根据三角形高的定义可得∠ADC＝∠BEC＝90°，再证明∠EBC＝∠ DAC，然后再添加 AC＝BC 可利用 AAS 判定△ADC≌△BEC． 【解答】解：添加 AC＝BC， ∵△ABC 的两条高 AD，BE， ∴∠ADC＝∠BEC＝90°， ∴∠DAC+∠C＝90°，∠EBC+∠C＝90°， ∴∠EBC＝∠DAC， 在△ADC 和△BEC 中 ， ∴△ADC≌△BEC（AAS）， 故答案为：AC＝BC． 【点评】此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、 ASA、AAS、HL． 注意：AAA、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两 边一角对应相等时，角必须是两边的夹角． 14．【分析】直接利用旋转的性质结合扇形面积求法以及等边三角形的判定与性质得出 S 阴影＝S 扇形 ADE﹣S 弓形 AD＝S 扇形 ABC﹣S 弓形 AD，进而得出答案． 【解答】解：连接 BD，过点 B 作 BN⊥AD 于点 N， ∵将半径为 4，圆心角为 90°的扇形 BAC 绕 A 点逆时针旋转 60°， ∴∠BAD＝60°，AB＝AD， ∴△ABD 是等边三角形， ∴∠ABD＝60°， 则∠ABN＝30°， 故 AN＝2，BN＝2 ， S 阴影＝S 扇形 ADE﹣S 弓形 AD＝S 扇形 ABC﹣S 弓形 AD ＝ ﹣（ ﹣ ×4× ） ＝ ． 故答案为： ． 【点评】此题主要考查了扇形面积求法以及等边三角形的判定与性质，正确得出△ABD 是等边三 角形是解题关键． 15．【分析】分别求得使关于 x 的不等式组 有解，且使关于 x 的一元一次方程 +1 ＝ 的解为负数的 a 的值满足的条件，然后利用概率公式求解即可． 【解答】解：∵使关于 x 的不等式组 有解的 a 满足的条件是 a＞﹣ ， 使关于 x 的一元一次方程 +1＝ 的解为负数的 a 的 a＜ ， ∴使关于 x 的不等式组 有解，且使关于 x 的一元一次方程 +1＝ 的解为负 数的 a 的值为﹣1，0，1，三个数， ∴使关于 x 的不等式组 有解，且使关于 x 的一元一次方程 +1＝ 的解为负 数的概率为 ， 故答案为： ． 【点评】本题考查了概率公式、一元一次方程的解及解一元一次不等式组的知识，解题的关键是 首先确定满足条件的 a 的值，难度不大． 16．【分析】连接 BO 与 ED 交于点 Q，过点 Q 作 QG⊥x 轴，垂足为 G，可通过三角形全等证得 BO 与 ED 的交点就是 ED 的中点 F，由相似三角形的 性质可得 S△OGF＝ S△OCB，根据反比例函数比 例系数的几何意义可求出 k，从而求出 S△OAE，进而可以得到 AB＝4AE，即 BE＝3AE．由轴对称 的性质可得 OE＝BE，从而得到 OE＝3AE，也就有 AO＝2 AE，根据△OAE 的面积可以求出 AE， OA 的值．易证四边形 OAEH 为矩形，从而得到 EH＝OA，就可求出 EH 的值． 【解答】解：连接 BO 与 ED 交于点 Q，过点 Q 作 QN⊥x 轴，垂足为 N，如图所示， ∵矩形 OABC 沿 DE 翻折，点 B 与点 O 重合， ∴BQ＝OQ，BE＝EO． ∵四边形 OABC 是矩形， ∴AB∥CO，∠BCO＝∠OAB＝90°． ∴∠EBQ＝∠DOQ． 在△BEQ 和△ODQ 中， ． ∴△BEQ≌△ODQ（ASA）． ∴EQ＝DQ． ∴点 Q 是 ED 的中点． ∵∠QNO＝∠BCO＝90°， ∴QN∥BC． ∴△ONQ∽△OCB． ∴ ＝（ ）2＝（ ）2＝ ． ∴S△ONQ＝ S△OCB． ∵S 矩形 OABC＝8 ， ∴S△OCB＝S△OAB＝4 ． ∴S△ONQ＝ ． ∵点 F 是 ED 的中点， ∴点 F 与点 Q 重合． ∴S△ONF＝ ． ∵点 F 在反比例函数 y＝ 上， ∴ ＝ ． ∵k＜0， ∴k＝﹣2 ． ∴S△OAE＝ ＝ ． ∵S△OAB＝4 ， ∴AB＝4AE． ∴BE＝3AE． 由轴对称的性质可得：OE＝BE． ∴OE＝3AE．OA＝ ＝2 AE． ∴S△OAE＝ AO•AE＝ ×2 AE×AE＝ ． ∴AE＝1． ∴OA＝2 ×1＝2 ． ∵∠EHO＝∠HOA＝∠OAE＝90°， ∴四边形 OAEH 是矩形． ∴EH＝OA＝2 ． 故答案分别为：﹣2 、2 ． 【点评】本题考查了反比例函数比例系数的几何意义、轴对称的性质、全等三角形的判定与性质、 矩形的判定与性质、相似三角形的判定与性质等知识，有一定的综合性． 三．解答题（共 7 小题） 17．【分析】原式第二项利用除法法则变形，约分后两项通分并利用同分母分式的减法法则计算得 到最简结果，利用非负数的性质求出 x 与 y 的值，代入计算即可求出值． 【解答】解：原式＝1﹣ • ＝1﹣ ＝ ＝﹣ ， 由|x﹣2|+（2x﹣y﹣3）2＝0，得到 ， 解得： ， 则当 x＝2，y＝1 时，原式＝﹣ ． 【点评】此题考查了分式的化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键． 18．【分析】（1）要关于 y 轴对称，即从各顶点向 y 轴引垂线，并延长，且线段相等，然后找出各 顶点的坐标． （2）各顶点向右平移 6 个单位找对应点即可． （3）从图中可以看出关于直线 x＝3 轴对称． 【解答】解：（1）A1（0，4），B1（2，2），C1（1，1）； （2）A2（6，4），B2（4，2），C2（5，1）； （3）△A1B1C1 与△A2B2C2 关于直线 x＝3 轴对称． 【点评】本题侧重于数学知识的综合应用，做这类题的关键是掌握平移，轴对称，及坐标系的有 关知识，触类旁通． 19．【分析】（1）设购进 A 种服装 x 件，购进 B 种服装 y 件，根据总价＝单价×数量结合总利润＝ 单件利润×销售数量，即可得出关于 x、y 的二元一次方程组，解之即可得出结论； （2）根据少获得的总利润＝单件少获得的利润×销售数量，即可求出结论． 【解答】解：（1）设购进 A 种服装 x 件，购进 B 种服装 y 件， 根据题意得： ， 解得： ． 答：购进 A 种服装 40 件，购进 B 种服装 20 件． （2）40×100×（1﹣0.9）+20×160×（1﹣0.8）＝1040（元）． 答：服装店比按标价出售少收入 1040 元． 【点评】本题考查了二元一次方程组的应用，解题的关键是：（1）找准等量关系，正确列出二 元一次方程组；（2）根据数量关系，列式计算． 20．【分析】（1）易证∠ACD＝∠BCE，即可求证△ACD≌△BCE，根据全等三角形对应边相等可 求得 AD＝BE，根据全等三角形对应角相等即可求得∠AEB 的大小； （2）易证△ACD≌△BCE，可得∠ADC＝∠BEC，进而可以求得∠AEB＝90°，即可求得 DM＝ ME＝CM，即可解题． 【解答】解：（1）∵∠ACB＝∠DCE，∠DCB＝∠DCB， ∴∠ACD＝∠BCE， 在△ACD 和△BCE 中， ， ∴△ACD≌△BCE（SAS）， ∴AD＝BE，∠CEB＝∠ADC＝180°﹣∠CDE＝120°， ∴∠AEB＝∠CEB﹣∠CED＝60°； （2）∠AEB＝90°，AE＝BE+2CM， 理由：如图 2， ∵△ACB 和△DCE 均为等腰直角三角形， ∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°， ∴∠ACD＝∠BCE． 在△ACD 和△BCE 中， ， ∴△ACD≌△BCE（SAS）， ∴AD＝BE，∠ADC＝∠BEC． ∵△DCE 为等腰直角三角形， ∴∠CDE＝∠CED＝45°， ∵点 A、D、E 在同一直线上， ∴∠ADC＝135°． ∴∠BEC＝135°， ∴∠AEB＝∠BEC﹣∠CED＝90°． ∵CD＝CE，CM⊥DE， ∴DM＝ME． ∵∠DCE＝90°， ∴DM＝ME＝CM， ∴AE＝AD+DE＝BE+2CM． 【点评】本题考查了全等三角形的判定，考查了全等三角形对应边相等、对应角相等的性质，本 题中求证△ACD≌△BCE 是解题的关键． 21．【分析】（1）变形为不定方程 k（x﹣4）＝y﹣4，然后根据 k 为任意不为 0 的实数得到 x﹣4＝ 0，y﹣4＝0，然后求出 x、y 即可得到定点的坐标； （2）通过解方程组 得 A（6，3）、B（﹣4，8）； ① 如图 1，作 PQ∥y 轴，交 AB 于点 Q，设 P（x， x2﹣x），则 Q（x，﹣ x+6），则 PQ＝ （﹣ x+6）﹣（ x2﹣x），利用三角形面积公式得到 S△PAB＝﹣ （x﹣1）2+ ＝20，然后解 方程求出 x 即可得到点 P 的坐标； ② 设 P（x， x2﹣x），如图 2，利用勾股定理的逆定理证明∠AOB＝90°，根据三角形相似的 判定，由于∠AOB＝∠PCO，则当 ＝ 时，△CPO∽△OAB，即 ＝ ；当 ＝ 时，△CPO∽△OBA，即 ＝ ，然后分别解关于 x 的绝对值方程即可得到对应 的点 P 的坐标． 【解答】解：（1）∵y＝kx﹣4k+4＝k（x﹣4）+4， 即 k（x﹣4）＝y﹣4， 而 k 为任意不为 0 的实数， ∴x﹣4＝0，y﹣4＝0，解得 x＝4，y＝4， ∴直线过定点（4，4）； （2）当 k＝﹣ 时，直线解析式为 y＝﹣ x+6， 解方程组 得 或 ，则 A（6，3）、B（﹣4，8）； ① 如图 1，作 PQ∥y 轴，交 AB 于点 Q， 设 P（x， x2﹣x），则 Q（x，﹣ x+6）， ∴PQ＝（﹣ x+6）﹣（ x2﹣x）＝﹣ （x﹣1）2+ ， ∴S△PAB＝ （6+4）×PQ＝﹣ （x﹣1）2+ ＝20， 解得 x1＝﹣2，x2＝4， ∴点 P 的坐标为（4，0）或（﹣2，3）； ② 设 P（x， x2﹣x），如图 2， 由题意得：AO＝3 ，BO＝4 ，AB＝5 ， ∵AB2＝AO2+BO2， ∴∠AOB＝90°， ∵∠AOB＝∠PCO， ∴当 ＝ 时，△CPO∽△OAB， 即 ＝ ， 整理得 4| x2﹣x|＝3|x|， 解方程 4（ x2﹣x）＝3x 得 x1＝0（舍去），x2＝7，此时 P 点坐标为（7， ）； 解方程 4（ x2﹣x）＝﹣3x 得 x1＝0（舍去），x2＝1，此时 P 点坐标为（1，﹣ ）； 当 ＝ 时，△CPO∽△OBA， 即 ＝ ， 整理得 3| x2﹣x|＝4|x|， 解方程 3（ x2﹣x）＝4x 得 x1＝0（舍去），x2＝ ，此时 P 点坐标为（ ， ）； 解方程 3（ x2﹣x）＝﹣4x 得 x1＝0（舍去），x2＝﹣ ，此时 P 点坐标为（﹣ ， ） 综上所述，点 P 的坐标为：（7， ）或（1，﹣ ）或（﹣ ， ）或（ ， ）． 【点评】本题考 查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征和相似三角形的判 定方法；会利用待定系数法求抛物线解析式，通过解方程组求两函数图象的交点坐标，会解一元 二次方程；理解坐标与图形性质；会运用分类讨论的思想解决思想问题． 22．【分析】（1）利用 360 度乘以对应的百分比即可求解； （2）利用加权平均数公式即可求得平均数，然后求得乙组中具体的分数即可求得方差、众数、 中位数； （3）根据实际情况提出即可． 【解答】解（1）360×（1﹣20%﹣20%﹣10%﹣10%）＝360×40%＝144，故答案是 144． （2）乙组的平均分是：8×40%+7×20%+6×20%+3×10%+9×10%＝7（分）， 乙组的总人数是：2+1+4+1+2＝10（人），[来源:学科网] 则得 9 分的有 1 人，8 分的 4 人，7 分的 2 人，6 分的 2 人，3 分的 1 人， 则方差是： [（9﹣7）2+4×（8﹣7）2+2×（7﹣7）2+2×（6﹣7）2+（3﹣7）2]＝2.6，众数 是 8，中位数是 7.5． （3）乙组的众数高于甲组；乙组的中位数高于甲组． 【点评】本题考查的是条形 统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得 到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接 反映部分占总体的百分比大小． 23．【分析】（1）利用直线表达式求出点 A、B 的坐标，把这两个点的坐标代入二次函数表达式即 可求解； （2）利用两个三角形夹角相等、夹边成比例，即可证明△BOD∽△AOB； （3）证明△BCP∽△BAC，则 ＝ ，求出 BP 的长度，即可求解． 【解答】解：（1）∵抛物线 y＝ax2﹣4ax+4 经过点 A 和点 B，点 B 在 y 轴上， ∴当 x＝0 时，y＝4， ∴点 B 的坐标为（0，4）， ∵直线 y＝﹣ x+b 与 x 轴相交于点 A，与 y 轴相交于点 B， ∴b＝4， ∴直线 y＝﹣ x+4， 当 y＝0 时，x＝8， ∴点 A 的坐标为（8，0）， ∵抛物线 y＝ax2﹣4ax+4 经过点 A 和点 B， ∴a×82﹣4a×8+4＝0，解得，a＝ ， ∴抛物线 y＝﹣ x2+ x+4； （2）证明：∵y＝﹣ x2+ x+4＝﹣ + ，该抛物线的对称轴与 x 轴相交于点 D， 令 y＝0，解得：x＝﹣4 和 8，则点 C 的坐标为（﹣4，0），即：OC＝4， ∴点 D 的坐标为（2，0），∴OD＝2， ∵ 点 B（0，4）， ∴OB＝4， ∵点 A（8，0）， ∴OA＝8， ∴ ， ， ∴ ， ∵∠BOD＝∠AOB＝90°， ∴△BOD∽△AOB； （3）连接 CP，∵△BOD∽△AOB， ∴∠OBD＝∠BAO＝ α ，∠BCP＝∠DBO＝ α ， ∴∠BCP＝∠BAO＝ α ，而∠CPB＝∠CBP， ∴△BCP∽△BAC，则 ＝ ， 其中，BC＝4 ，AB＝4 ，代入上式并解得：BP＝ ， 过点 P 作 x 轴的平行线交 y 轴于点 H， ∵PH∥x 轴， ∴ ＝ ， 即： ＝ ，解得：PH＝ ， 即：点 P 的横坐标为： ， 同理可得其纵坐标为 ， 即点 P 的坐标为（ ， ）． 【点评】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养，要会利用数 形结合的思想把代数和几何图形结合起来，利用三角形相似求出线段的长度．